International Journal of Public Health

An Opinion Note: Graph Theory Approaches in Healthcare Inventory System

S Priyan* and R Gurusamy

Department of Mathematics, Mepco Schlenk Engineering College, Virudhunagar 626005, Tamil Nadu, India

Submission: November 7, 2017; Published: November 20, 2017

*Corresponding author: S Priyan, Department of Mathematics, Mepco Schlenk Engineering College, Virudhunagar 626005, Tamil Nadu, India, Tel: +919543647190; Email: jaisilpriyan@gmail.com

How to cite this article: Priyanka T, A K Bakhshi b. Metaheuristic Crafting of Organic Donor-Acceptor-Donor Copolymers. Organic & Medicinal Chem IJ. 2017; 2(5): 555598. DOI: 10.19080/JOJPH.2017.02.555598.

Abstract

Graph theory is a very natural and powerful tool in combinatorial operations research. Some important operations research problems particularly inventory control problem that can be solved using graphs. A brief review of graph theory applications to problems of inventory systems are made in this paper. It suggests the possibilities which exist for improving the operational, tactical and strategic decision-making of health care inventory systems through the use of graph theory approaches. This article aims to raise the awareness of healthcare managers and inventory researchers with regard to realistic graph theory applications.

Keywords: Graph theory; Inventory; Healthcare; Optimization

Literature Review

The research in graph theory has started in the thirties by König [1]. Afterwards many deep research problems like planarity [2], graph minors [3] and other fundamental problems[4] have been addressed. Seminal work was done by Harary[5] who investigated numerous problems in graph theory. In the nineteen's, many other emerging areas in graph theory such as External Graph Theory [6], Random Graph Theory [7] and Algebraic Graph Theory [8] have been established. Recently, Bisen [9] addressed the application of Graph theory in Operations Research. There is no doubt that graph-theoretical approaches and methods have been applied extensively in many areas particularly inventory management.

Geetha and Sekar [10] presented the detailed methodology of Graph theory matrix approach. Also they provided the application of Graph theory matrix approach for the analysis and evaluation of optimal combination of operating parameters of a diesel engine. In recent years, applications of graph theory have proliferated across the academic spectrum. Whereas operations research has made rich use of graph theory, its use seems limited in optimization, and particularly in healthcare inventory system. Common applications of graph theory - analyses of connectivity, path or transport efficiencies, sub networks, network structure, system behavior and dynamics, and network optimization or engineering - all have uses or potential uses in operations research and closely related fields. On the other hand, in this paper, we give a short introduction to graph theory in the field of inventory and supply chain. Based on literature review and experts opinion, we suggest some possible research in the field of healthcare inventory and supply chain system through graph theory approach.

Revenue management is a business principle that balances supply and demand to control price and/or inventory availability in order to maximize revenue and profit growth. In this connection, Kuyumcu and Garcia-Diaz [11] developed a new analytical procedure for joint pricing and seat allocation problem considering demand forecasts, number of fare classes, and aircraft capacities through polyhedral graph theoretical approach. They stated that this approach has a potential utilization in such service and transportation related industries as lodging, car rental, trucking, cargo, broadcasting, manufacturing, energy, and health care. Based on Kuyumcu and Garcia-Diaz [11] suggestion, we can investigate a new analytical procedure for joint pricing and seat allocation inventory problem under realistic troubles in health care industries Faisal et al. [12] presented a conceptual framework which models various variables associated with risk mitigation environment along with their interdependencies using graph theory and matrix methods. The Risk Mitigation Environment (RME) is quantified and presented in the form of a single numerical index in their paper.

Their proposed model is quite versatile from the attitude that it provides an opportunity to integrate new variables which could impact the overall supply chain risk mitigation environment along with the potential to benchmark supply chains on risk mitigation dimension. In today's business environment, harsher and more frequent natural and man-made disasters make supply chains more vulnerable. Wagner and Bode [13] stated that “supply chain vulnerability is a function of certain supply chain characteristics and that the loss a firm incurs is a result of its supply chain vulnerability to a given supply chain disruption”. Although many researchers offered models of supply chain vulnerability, Wagner and Neshat [14] developed an approach based on graph theory to quantify and hence mitigate supply chain vulnerability.

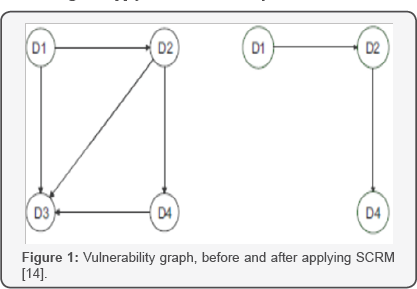
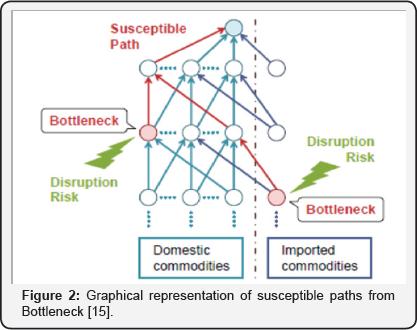
They demonstrated in their article that graphs can be used as visual maps that facilitate the understanding of supply chain vulnerability and support decision making in Supply Chain Risk Management (SCRM). Also they said that given managers' limited amount of resources such as time and money, the graph theoretical approach presented in their article (Figure 1) can help managers to make effective and efficient decisions and allocate an appropriate amount of resources to a particular supply chain vulnerability driver. The graph in Figure 1 shows vulnerabilities and their interdependencies in a supply chain [14], Nakatani et al. [15] recently developed a graph theory- based methodology for assessing supply chain vulnerability to disruption risks by identifying bottleneck raw materials whose supply disruptions could severely affect a focal product's supply chain. A supply chain structure is modeled by a directed graph and its adjacency matrix, adapted from physical input-output data in the LCI database. The reachability components in the supply chain are identified by Boolean matrix calculations. Also they identified and illustrated graphically (Figure 2) susceptible paths from the bottlenecks. Mallick et al. [16] demonstrated a new approach by integrating Graph Theory and the Analytic Hierarchy Process (AHP) as a decision analysis tool for multicriteria inventory classification. Output of their hybrid method shows more precise results than that of either traditional ABC or the AHP classification methods. Recently a large number of inventory model through graph theory publications concentrate their concepts and analysis on the forward supply chain (Figure 2).

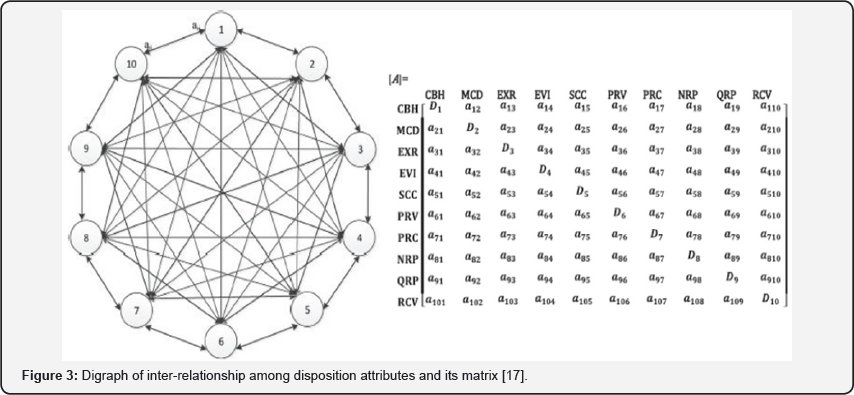
Reverse logistics has become an essential part of business because of legislation, environmental concerns, and corporate social responsibility. Disposition decision plays an important role in the performance of reverse logistics. Perusal of previous literature indicates that there are very few studies related to disposition of returned products in reverse logistics. Agrawal et al. [17] explored the various disposition alternatives and developed an approach for the selection of best disposition alternative using Graph Theory and Matrix Approach (GTMA). In GTMA, nodes and edges are two basic elements, which represent the inter-relationship between nodes (different attributes) in the form of digraph and in the form of matrix. These nodes represent the attributes. Agrawal et al. [17] assumed that the digraph consists of a set of nodes N={n_i} where i=1,2,3,--,Mand a set of directed edgeE={a_ij}. They selected 10 attributes for the selection of disposition alternative. Agrawal et al. [17] drew a digraph for the 10 number of attributes which Also shown in (Figure 3) and represent them on a digraph so a matrix which is shown below.

Suggestion and Conclusion

The graph theory approaches reviewed in this paper can be applied to study the healthcare inventory system. However, till to date, none of the authors developed healthcare system based inventory model using graph theory. Therefore, based on the literature review, we suggest some possible research in the field of healthcare inventory system using graph theory approach.

a) It extends the model of Kuyumcu and Garcia-Diaz [11] for a pharmaceutical company - hospital supply chain to bring in an important factor such as patient service level. In addition, many developed countries have always maintenance check of pharmaceutical products on a Healthcare system as safety is the highest priority. In view of this Kuyumcu and Garcia-Diaz [11] model could also be extended by assuming the production process is interrupted regularly for maintenance so as to avoid major failures and supply disruptions.

b) We may use Geetha and Sekar [10]'s Graph theory matrix approach in Uthayakumar and Priyan [18] model to find the optimal strategies of pharmaceutical companyhospital supply chain.

c) We can extend all the existing healthcare inventory models by using Faisal et al. [12]'s graph theory and matrix methods. Then Wagner and Neshat [14] can be used to facilitate the understanding of supply chain vulnerability and support decision making in Healthcare Supply Chain.

d) We may use integrating Graph Theory and the Analytic Hierarchy Process [16] in existing healthcare inventory models instead of traditional ABC or the AHP classification methods. Further, Agrawal et al. [17]'s method can be used in reverse healthcare supply chain.

A brief review of graph theory applications to inventory system are addressed and suggested some possible healthcare research through graph theory approach in this paper. The purpose of this paper is to identify the existing inventory literature on the wide range of graph theory studies applied to healthcare, and to classify studies based on application type and on the graph theory technique employed. This paper demonstrates some opinion to utilize graph theory in healthcare for the worldwide researchers.