International Journal of Public Health

Review Article

Operations Research in Healthcare: A Review

*S Priyan

Department of Mathematics, Mepco Schlenk Engineering College, Sivakasi 626005, Virudhunagar DT, Tamilnadu, India.

Submission: February 21, 2017; Published: March 16, 2017

*Corresponding author: S Priyan, Department of Mathematics, Mepco Schlenk Engineering College, Sivakasi 626005, Virudhunagar DT, Tamilnadu, India,Email: jaisilpriyan@gmail.com

How to cite this article: S Priyan. Operations Research in Healthcare: A Review. JOJ Pub Health. 2017; 1(3): 555561. DOI:10.19080/JOJPH.2017.01.555561

Abstract

A brief review of operations research (OR) applications to problems of health care systems are made in this article. It demonstrates the possibilities which exist for improving the operational, tactical and strategic decision-making of health care systems through the use of operations research approaches. This paper aims to raise the awareness of healthcare managers with regard to realistic OR applications

Commentary

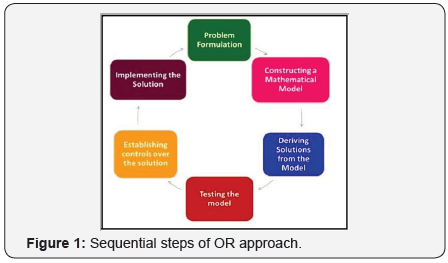
Operations research is a term that can be used with mathematical and statistical methods and computer systems, which characterizes the orientation, interdisciplinary philosophy, which aims to quantify the relevant aspects of the situation in the modeling and manipulation of the model approach to develop decisions, plans, and policies. The systematic methodology of OR focuses on the problems developed conflicting objectives, strategies and alternatives. OR is, ultimately, the scientific method, which is applied to complex tasks to assess the overall impact of different policy options to consider actions, providing a better basis for making business decisions. The OR approach to solve the problem comprises the following six sequential steps:

Formulate the problem,
Construct a mathematical model,
Derive the solution from the model,
Test the model
Establish control over the solution, and

Establish control over the solution, and

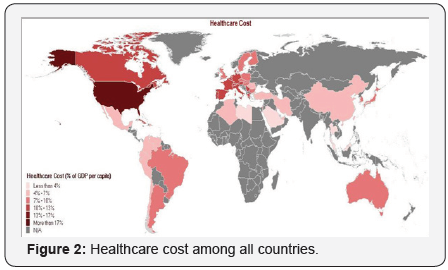
Health care is the number one domestic industry in the United States and one of the largest industries in the developed and developing countries, as well as it is a service-oriented industry. It is a particularly significant service industry given not only the criticality of quality and safety in delivering patient care [1], but also the associated cost involved as it is expected to account for 20% of gross domestic product (GDP)or $4 trillion in the USA in 2015 [2]. Figure 2 compares the total expenditure on health care among several countries, as a percentage of the GDP. These concerns extend beyond the USA, leading to increasing research interest in global healthcare operations [3]. OR provides a broad range of methodologies that can help health care systems to significantly improve their operations. Technologies, tools and theories of decision-making OR is many different topics and issues in health care. There are at least three reasons why operations research is relevant to health. To improve programme outcomes in relation to medical care or prevention, to assess the feasibility of new strategies orinterventions in specific settings or populations, and we have toadvocate policy change [4] (Figure 2).

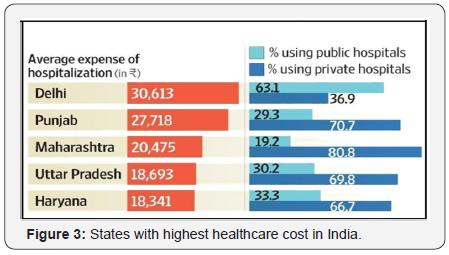
Healthcare has become one of India’s largest sectors bothin terms of revenue and employment. Healthcare compriseshospitals, medical devices, clinical trials, outsourcing,telemedicine, medical tourism, health insurance and medicalequipment. The Indian healthcare sector is growing at a briskpace due to its strengthening coverage, services and increasingexpenditure by public as well private players. Indian healthcaredelivery system is categorized into two major components publicand private. The Government, i.e. public healthcare systemcomprises limited secondary and tertiary care institutions inkey cities and focuses on providing basic healthcare facilitiesin the form of primary healthcare centers (PHCs) in rural areas.The private sector provides majority of secondary, tertiary andquaternary care institutions with a major concentration inmetros, tier I and tier II cities. India’s competitive advantage liesin its large pool of well-trained medical professionals. India isalso cost competitive compared to its peers in Asia and Westerncountries. The cost of surgery in India is about one-tenth of thatin the US or Western Europe. The comparison of a few Indianmajor states with highest healthcare cost is given in (Figure 3).

Demographic change and increasing health expenditures inthe world make the healthcare research a hot topic. Hospitalsin the world are becoming larger to take advantage of thescale economy but also become more complex to design and tooperate. Ageing population makes constant diseases increasinglysignificant and leads to the need of better disease prevention,diagnostic, treatment planning and proactive cares. Patients aremore and more concerned by healthcare safety and traceability.Healthcare systems are also changing and new health servicessuch as home healthcare and telemedicine are growing. Mosthospitals used to empiric management are not prepared forand innovative systems engineering approaches are needed.Recent development of advance medical technologies makesthe systems engineering approach possible. The increasingavailability of healthcare relevant data makes possible betterdisease prevention, diagnostic and healthcare system operations.Innovative OR techniques have been designed for a broad rangeof healthcare applications such as operating room planning, emergency department staffing, breast cancer screening,radiotherapy treatment planning, home healthcare planning,long-term care planning and scheduling.

Facing these challenges, the very first attempts of thehospitals are to apply modern management techniques fromother industries. This leads to numerous hospital projectson lean management, quality control, inventory control, etc.Most of these projects had limited impacts due to their strongdependence on experiences of consulting firms gained from otherindustries and hardly took into specific features of. Hospitalsrealized more and more the need of original research takinginto specific features of healthcare industry. Various scientificcommunities quickly embraced major healthcare challengesfrom different perspectives. Emerging hot topics of the robotics& automation community include lab automation, lab-on-chip,surgical navigation, nanoscale drug delivery, medical imaginganalysis, etc. Other communities such as OR and IndustrialEngineering have been very active in healthcare managementresearch. Major Operations Research and Industrial Engineeringjournals publish more and more papers in healthcare and OR/IEconferences often have very popular sessions in healthcare suchas surgery planning/scheduling, nurse rostering, emergencydepartment analysis, ambulance location/dispatching and so on.

Operations research is increasingly recognized as essentialto strengthen health programs. For example, expanded stoptuberculosis (TB) strategy research clearly acting as a keyelement of successful programs of TB. It has various definitionsdepending on the scenario, scientists, and the type of search.The International Union against TB and Lung Disease and manyof its research partners define OR as research into strategies,interventions, tools or knowledge that can enhance the quality,coverage, effectiveness or performance of the health system orprogramme in which the research is being conducted [4]. Mistryet al. [5] derived a local agenda for OR: modeling the effects ofnewer technologies, active case detection, and changes in timingof activities, and mapping hotspots and contact networks;modeling the effects of drug control, changing the balance ofambulatory and inpatient care, and adverse drug reactions;modeling the effects of integration of TB and HIV diagnosis andmanagement, and preventive drug therapy; and modeling theeffects of initiatives to improve infection control.

Healthcare OR is not a new field; many health careresearchers and planners use concepts and methodologies which,in the business world, are often associated with the practice ofoperations research. These concepts and methodologies mostoften deal with problems in the areas of: Healthcare operationsimprovement; Inventory and Supply chain management; Facilitylocation and layout; Prevention, detection and treatment ofdiseases; Resource allocation; Clinical diagnosis and decisionmaking; and Treatment design and planning. In the contextof matter and the flow of patients and healthcare logisticsmanagement operations offer a wide range of applications for the analysis of operations research techniques. We review belowthe applications area of OR in healthcare.

Operations Research in Healthcare: Literature Review

An area that has received considerable attention amongOR scholars is workforce scheduling, and in particular, nurserostering. The problem of working hours of construction fornurses to meet fluctuations in demand is extremely difficult.Service plans must comply with the requirements of the work ofnurses distinguish permanent and temporary staff are qualifiedto provide holidays and day, night and nurses evenly over theweekend and set preferences for class officers. Linear, mixedinteger and goal programming with constraint programmingmethods have been developed to generate nurse rosters [6].Reviews of literature on nurse rostering are available in Burke etal. [7] and Lim et al. [8].

Appointment scheduling has also been a rich research areaover the past decades (e.g. see Gupta and Denton [9]). Theprocess of assigning time slots for serving out- and inpatientsarises in diagnostic and treatment units deals with uncertainservice times, no-shows, cancelations, and walk-ins. A goodappointment schedule keeps patient waiting times short andminimizes staff overtime taking into account the patient loadand the available resources (i.e. staff, rooms, and equipment)?In view of this numerous authors developed models with theobjective of

How many patients to schedule?
How to allocate appointment slots throughout workingday?
What is the optimal sequencing of heterogeneouspatients.

Recently, Granja et al. [10] developed an optimizationmodel based on simulation approach to the patient admissionscheduling problem using a linear programming algorithm.Richard et al. [11] provided an improved method for solvingthe so-called dynamic patient admission scheduling (DPAS)problem. Atlie et al. [12] presented an exact method for PatientAdmission Scheduling (PAS) problem based on a recursivelogic-based Benders’ decomposition where each sub problemis formulated as an integer linear program. Turhan et al. [13]addressed two Mixed Integer Programming based heuristicsnamely Fix-and-Relax and Fix-and-Optimize where PAS probleminstances are decomposed into sub-problems and then the subproblemsare optimized.

Kidney dialysis therapy initiation for evaluating costand effectiveness is investigated in Lee et al. [14]. They usedApproximate Dynamic Programming and Simulation todetermine an optimal therapy and a strategy for maximizingpatient welfare. Chen [15] proposed the kidney allocationproblem. He assumed that the decision has to be made within a fixed time horizon because a kidney is perishable and the kidneysare limited. He addressed that the objective of kidney allocationproblem is to determine the allocation rule to maximize the totalexpected value achieved. The arrival, demand pattern of patientsis random. When we replace kidneys with airline tickets andpatients with travelers, we get the airline yield managementproblem. When we replace kidney and patient by job and workerrespectively, it has the typical scheduling problem. Recently,Thamer et al. [16] developed a risk score to assist shareddecision making for kidney dialysis initiation. Then Bagshaw etal. [17] addressed strategies for the optimal timing to start renalreplacement therapy in critically ill patients with acute kidneyinjury

Operating theater planning and scheduling (OTPS) has alsoreceived much attention in the past 60 years. The strategic(long term) planning level addresses capacity planning given aforecast of patient demand. Typically, the operating theaters andthe time allocated to each activity of the department at the time.The tactical (mid-term) planning level deals with the creationof weekly/monthly (rough) schedules for elective surgeries.Operational planning, the operational plan for the next day,generating a sequence of operations in each operating roomearly and distribution activities and some resources. Finally,the online planning level deals with rescheduling previouslyplanned surgeries as a result of unforeseen events such asdelays, emergencies, and cancelations. The rich and still growingliterature on OTPS covers a wide range of OR methodologies(heuristic approaches, and simulation) for deterministic andstochastic environments [6]. Reviews of literature up to 2010on Operating Theater planning and scheduling are available inCardoen et al. [18]. Recently, Wang et al. [19] investigated anoperating theater allocation problem with uncertain surgeryduration and emergency demand. In Wang et al. [19], theoperating room allocation problem with cancellation risk ismathematically formulated as follows:

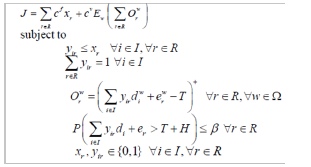
Strategic operating theater planning belongs to the group ofresource allocation and capacity planning problems. This groupinvolves decisions concerning the mix and volume of patientstreated by a hospital and the amount, capability, and type ofresources for the delivery of healthcare. Hospital layout planningis also at the strategic level, but has received much less attention.The goal is to design a hospital, a clinic or a department in orderto minimize the movements of patients and accompanyingresources such as medical staff and equipment [6]. Quadraticinteger programming models were proposed by Butler et al. [19] and Elshafei [20] for problems arising in this area.

Patient transportation is a variant of the dial-a-ride problem(DARP) and concerns finding a set of minimum-cost routesand schedules for a feet of ambulances (or hospital staff) totransport (or escort) inpatients between nursing wards anddiagnostic units. Hospital-specific constraints (e.g. differentpriorities of requests, needs special equipment and supportmedical staff during transport and handling of incompleteknowledge in advance) significantly complicate the developmentof high-quality vehicle routes and schedules. The latter is oftencontrolled by the imposition of the travel time of the patient andminimizing deviations from the desired times for pickup anddelivery [21]. By its nature DARP combined extremely difficultto solve, which has contributed to the development of new OR,in particular the new (meta-) heuristic methods allowed [6].Beaudry et al. [22] and Kergosien et al. [23] proposed tabusearch based approaches, while Hanne et al. [24] embedded anevolutionary algorithm in a software application designed tosupport all phases of the transportation flow including requestbooking, scheduling, dispatching, monitoring, and reporting.Recently, Knyazkov et al. [25] illustrated the evaluation ofDynamic Ambulance Routing for the Transportation of Patientswith Acute Coronary Syndrome in Saint-petersburg. Zhang et al.[26] addressed a real-life public patient transportation problemderived from the Hong Kong Hospital Authority (HKHA), whichprovides ambulance transportation services for disabled andelderly patients from one location to another.

Aiming at improving the efficiency and reliability ofambulance service, several location models for ambulancestations have been proposed in the OR literature. Well-knownapproaches to this problem are coverage model and medianmodel. Coverage model looks for the location to maximize the(deterministic or probabilistic) covered demand of ambulancecalls. Hence this model can be thought of reliability orientedmodel. On the other hand in median model the objective is tominimize the total traveling distance of the ambulances fromthe station to the scene of call. This model gives more weightto the efficiency of ambulance operation [27]. Morohosi [27]addressed the comparison of those optimization models throughactual patient call data from Tokyo metropolitan area to showthe characteristics of each model and investigate a possibility ofimprovement in ambulance service.

Problem of patients overflow in wards is addressed byTeow [24] The demand of hospital’s inpatient beds by medicalspecialties changes according to patients’ volume over time.With no adjustments to the allocation of beds, the growingmismatch will result in unnecessary patients’ overflow. Thiswill lead to poor patient care, travel health workers redundantand the waiting bed. Hence, hospitals need to periodicallyreview their bed allocation by specialties. The bed reallocationexercise is typically a zero-sum game: some specialties will endup with more beds while others with fewer beds. Teow [24]suggested the structure of the patients overflow problem. Hefirst established bed demand for each specialty using patientday.He stated that the objective of the problem is to assign thebeds (i.e. decision variables) such that the specialties will endup with equitable bed occupancy rates (i.e. outcome), subjectto number of beds available (i.e. constraint). Litvak et al. [28]presented a mathematical method for computing the number ofregional beds for any given acceptance rate. In Litvak et al. [29],for blocking probability, they computed the famous Erlang lossformula

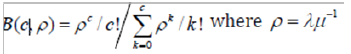
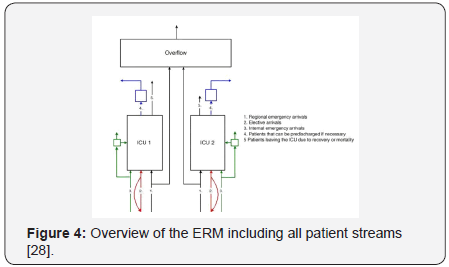
is the load, with λ the call arrival rate, and μ-1 the meancall length based Equivalent Random Method (ERM), and theyschematically depicted (Figure 4) the patient flows for two ICUs(Figure 4).

Outpatient appointment scheduling in health care has beenresearched over the last 50 years. Various scheduling rules havebeen proposed in different research works Bailey [30] and Cayirli[31]. A good appointment schedule is one that trade-offs patientswaiting time for clinics overtime, constrained by the patient loadand staffing. Operations research researchers use techniquessuch as queueing theory and discrete event simulation to proposevarious appointment strategies under different clinics settings.Some planning strategies can be very complex. Although the listof applications for logistics and research hospital managementoperation is far from over, above shows the range of possibilitiesin the field of operations research in hospitals [29].

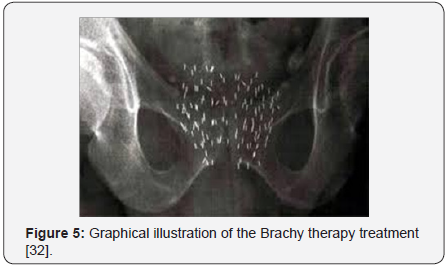
Optimization issues in healthcare have become noticeablysignificant and attract keen interest from the OR community.Chen [32] addressed the optimization and decision support inBrachy therapy treatment planning using OR techniques. Heexpressed that the planning means finding a pattern of sourcesthat is consistent with do simetric constraints in brachy therapy.He formulated the following objective (0-1 mixed integerprogramming) for the problem of Brachy therapy treatmentplanning and suggested the Branch and bound method to solveit: Objective = Rewards - Penalties, where the rewards are theeffect of the treatment and the penalties are the side-effect on the surrounding healthy tissues. The graphical illustration of the Brachy therapy treatment is shown in (Figure 5).

Minimization of the total treatment time in cancerradiotherapy using multileaf collimators is studied by Wakeet al. [14]. The approach considers a Mixed Integer Programthat happens to be a modification of a cutting-stock problemformulation. Maillart et al. [33] developed a Markov chainmodel for investigating the proper frequency of mammographyscreening. They analysed a broad range of screening policies anddiscussed computational results. Lee and Zaider [34] described aclinical decision support system for treatment planning in Brachytherapy (placement of radioactive seeds inside a tumour) andused Mixed Integer Program for optimization. Recently, Holder[35]) gave a comprehensive discussion of linear and non-linearprogramming models for Intensity Modulated RadiotherapyTreatment (IMRT). Nightingale et al. [36] surveyed the currentpractices of preparation and management of radical prostateradiotherapy patients during treatment.

Accurate demand forecasting is indispensable in healthcareplanning, it results providing the input to numerous optimizationproblems. Cote and Tucker [37] discussed four commonmethods for forecasting demand for healthcare services:percent adjustment, 12-month moving average, trendline andseasonality. Xue et al. [38] analysed the continued growth ofthe end-stage renal disease population in the United States.They forecasted up to the year 2010 using historical data withstepwise autoregressive and exponential smoothing models.The accuracies of various forecast methods were evaluated byJones et al. [39]. They used data from daily patient arrivals atthe emergency departments of three different hospitals andconsidered the following methods: time series regression,exponential smoothing, and seasonal autoregressive integratedmoving average and artificial neural network models.

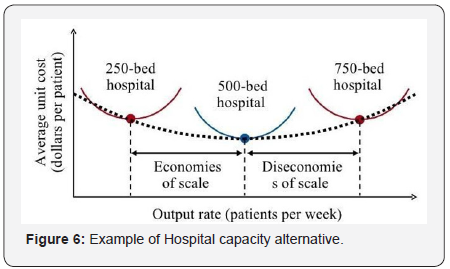
Hospital capacity planning is full of challenging problems forOR practitioners. Green and Savin [40] used OR-based analysesto address the increasingly critical hospital capacity planningdecisions. They used a queuing model formulation and gaveexamples of how OR models can be used for deriving significantinsights and operational strategies. Figure 6 shows the exampleof Hospital capacity alternative. A cooperative solution approach for hospital capacity to treat emergency patients inthe Netherlands is proposed in Litvak et al. [41]. Adan et al. [42]addressed the problem faced at a cardiothoracic surgery centerfor optimizing resource utilization. They modeled it as a MixedInteger Program having stochastic lengths of stay. Burdett& Kozan [43] proposed a multi-objective optimization (MOO)approach to perform a system wide analysis of public hospitalresources and capacity. Recently, Burdett et al. [44] deriveda mixed integer linear programming approach to performhospital capacity assessments. They developed the followingoptimization model

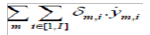
Minimize= subject to some realisticconstraint (Figure 6).

Increase in longevity, escalating health-care costs and theemergence of new diseases in recent years have forced medicaldecision-makers to focus strongly on preventive and specialized.According to Rais and Viana [45], optimization problems relatedto the prevention of diseases concern mostly vaccine selection.The vaccine selection algorithm has been extensively studiedas it was first introduced in Jacobson et al. [46]. Wu et al. [47]formulated the annual vaccine-strains selection problem as astochastic dynamic program. On the other hand, Earnshaw et al.[48] addressed a resource allocation problem for HIV preventionand developed a linear-programming model for improving onpast allocation strategies.

Unlike many industries, healthcare managers have tomanage very complicated distribution networks and inventorymanagement problems without proper guidance on efficientpractices. This is because most hospital administrators andpharmacy managers are doctors with expert knowledge inmedicine, and are not supply chain professionals. Hence, giventhe high costs, coordination, constraints, and perishability ofpharmaceuticals, more study is necessary to help health caremanagers in setting optimal supply chain management policies.Operations research provides a wide range of methodologies thatcan help hospitals and other health care systems to significantlyimprove their operations. Kelle et al. [49] provided decisionsupport tools that improve operational, tactical, and strategicdecision-making supply chain management under an inventory policy that involves periodic review. Amir et al. [50] developeda generalized network oligopoly model for PSC competition thattakes into account product perishability, brand differentiation,and discard costs. Priyan & Uthayakumar [51] designed thesupply chain management strategies for a pharmaceuticalcompany and a hospital. Priyan & Uthayakumar [52] framed anoptimal inventory management strategies for healthcare supplychain in a fuzzy–stochastic environment. Nematollahi et al. [53]derived an economic and social collaborative decision-making onvisit interval and service level in a two-echelon pharmaceuticalsupply chain.

Conclusion

A brief review of operations research (OR) applications tohealthcare system are addressed in this paper. The purposeof this paper is to identify the existing literature on the widerange of operations research (OR) studies applied to healthcare,and to classify studies based on application type and on theOR technique employed. Based on this review, we recognizedthat commonly used OR approaches fall into four categories:mathematical programming (deterministic and stochastic),heuristics, queuing theory, and simulation.