On the in Vivo Estimation of the Corneal Young's Modulus
Jia-Yush Yen1*, I-Jong Wang2, Po-Jen Shih3 and Hui-JyunTsao1
1Department of Mechanical Engineering, National Taiwan University, Taiwan
2Department of Ophthalmology, National Taiwan University, Taiwan
3Department of Civil and Environmental Engineering, National University of Kaohsiung, Taiwan
Submission: October 29. 2017; Published: November 22, 2017
*Corresponding author: Jia-Yush Yen, Department of Mechanical Engineering, National Taiwan University, 10617, Taipei, Taiwan, Tel: +886-2-33662688, Email: jyen@ntu.edu.tw
How to cite this article: Jia Y Y,Jong W,Jen S, Hui J T. On the in Vivo Estimation of the Corneal Young's Modulus. JOJ Ophthal. 2017; 5(4): 555670. DOI: 10.19080/JOJO.2017.05.555670.
Abstract
Today people are aware that the corneal biomechanical properties can affect the intraocular pressure (I0P) readings which could result in inaccurate diagnostics. Many researchers have focused on correcting the IOP readings by providing and using additional measurement information. Part of these efforts were directed toward the geometrical effects such as the central corneal thickness (CCT). Many researchers, on the other hand, believed the corneal biomechanical properties, the corneal elasticity and the corneal hysteresis (CH), may have greater influence on the IOP measurement. While the CH is already available from many new IOP measurement instruments, the corneal elasticity constant, namely the corneal Young's modulus, is not yet readily available. This mini review provides an introduction to the literature results to extract the corneal Young's modulus through the measurement data. The special focus is on those procedures that have the potential to be used for the Young's modulus estimation in vivo. This ruled out the finite element analysis results, which are many but are time consuming even for today's computer.
Keywords: Corneal Young's modulus; in vivo estimation; Corneal biomechanical models
Introduction
Corneal biomechanics is dimed to gain increased attention from the physicians. With the technology advancement, people now has more accesses to the detailed mechanism and the parameters involved in the corneal deformation. With the additional information, the ophthalmologists are now taking a closer look at many of the previously accepted examinations to achieve more accurate diagnostics.
Many researchers have stated that Goldmann applanation tonometry is flawed by the effects of different corneal parameters [1-4], and large numbers of patients could have been misclassified based on the IOP readings [3]. Many have contributed the error to the different central corneal thickness (CCT) as a major cause, and newer machines had also provided the physicians with a dependable measurement of the CCT [5-7]. However, later researches have also pointed out that there had been no effective nomogram available to account for the effect of CCT on the IOP readings [4,8]. With the introduction of Ocular Response Analyzer, the concept of Corneal Hysteresis (CH), the difference between the inward and the outward applanation pressures, also became available [4]. While researchers have reported CH as a potentially useful discriminator of the healthy eye from the ones suffering from pathological conditions, corneal ectasia or glaucoma [9,10], it has not been linked with the correction of the IOP measurements. Although the authors also did not totally rule out the possibility of finding more meaningful correlation in the future [1], his conclusion is mainly on the fact that the influence of the material properties alone on the IOP were larger than that of the CCT.
The above researches suggested that material properties directly affected the IOP and should be considered the primary factors when taking the measurements. In specific, this mini review will focus on the estimation of the corneal Young's modulus with special focus on the methods that shows potential for in vivo applications.
The Information available from current Measurement Machines
This review offers to look into the biomechanical models that are used in association with the IOP measurement instruments for in vivo estimation of the corneal material properties. Therefore, it is thus important to understand the information that could be obtained from the IOP instruments in use. With the increased attention on the corneal biomechanical properties, new instruments now provide many more parameters to help better understanding these properties.
The Ocular Response Analyzer (ORA) shines an infrared laser on the pupil and collect the reflected light as an air puff pushes the cornea into concave configuration to reach the required applanation [6]. The intensity of the reflected laser serves as an indicator of the shape of the cornea. By adjusting the position and orientation of the laser emitter and the collimation detector, one can synchronize the pick of the detected signal with cornea applanation. By comparing this response with the recorded air pressure, the ORA provides the time for the first applanation (P1), the second applanation (P2), the estimated Goldmann IOP (IOPG), and an estimate of the true IOP (IOPcc) corrected for the biomechanical properties of the cornea. The biomechanical properties extracted by the ORA are the corneal hysteresis (CH) and the corneal resistance factor (CRF). The CH is calculated as the difference between the two applanation pressures, . The CRF is derived from a formula, , where the value of the constant k is determined according to different P1 and P2 combinations. The ORA also came with a built-in ultrasound pachymeter that could provide the central corneal thickness (CCT) value when needed. One special feature of ORA is that it allows the user to extract the history of the pressure and light intensity responses.
Corvis ST is another machine that is gaining increased attention [5,7]. Corvis ST uses Scheimpflug imaging with high speed camera to record the cornea response under the air puff. The Corvis ST offers the 'A time-1/-2' (A1T and A2T) that are the times it took after the air puff to the first and the second applanation, the 'A length-1/-2' (A1L and A2L) that are the lengths of the flattened part of the cornea at the two applanation instances, the 'velocity-1/-2' (A1V and A2V) that are the velocities of the cornea when the first and the second applanation occurs. The 'highest concavity time' is the time it took for the cornea to reach the highest concavity, and the 'highest concavity curvature' (radius) is the corresponding central curvature radius. The 'peak distance' (PD) is the diameter of the annulus around the concaved cornea at the highest concavity, and the 'maximum deformation amplitude’ (DA) is distance traveled by the corneal apex to reach the highest concavity. And of course the CCT can be measured off the Scheimpflug images, and usually the lowest value is displayed.
These are the two non-contact tonometry instruments that have been receiving the widest attention [11,12]. Besides these, there are many other techniques based on different physical principles under research. These techniques includes the ultrasonic elastography [13], the ultrasonographic analysis [14], the optical coherence tomography [15], the Brillouin optical microscopy [16]. They have all attracted tremendous amount of attentions, some even show potential in direct in vivo cornea Young’s modulus measurement [13,14,16], but most of them are still in the laboratory test phase and are still waiting to become standard equipment. There are some nice review articles describing the various technologies [7,11,12].
The Static Corneal Biomechanical Modeling
Biomechanical model describes the cornea behavior when interacting with the environmental change. Although direct corneal Young's modulus tests still cannot be performed in vivo. The current available results were conducted on cadaver eyes [17-19]. It is still necessary to extract the corneal biomechanical properties by comparing the available IOP measurement results and fit them into the biomechanical models. This mini review will first introduce two most well-known mathematical models [20], namely the Orssengo-Pye algorithm [21] and the Sj0ntoft- Edmund algorithm [22], and then move on to some of the newer approaches. At this point, it is also a good place to introduce the concept of static model and dynamic model. The static corneal biomechanical model describes the static formation of the cornea. Basically, one deals with the static balance among all the forces applied. This is also the basis for the Goldmann tonometer [23] with the assumption that the corneal thickness is 520|im and the diameter of the flattened area is 3.06 mm. With the static assumption, one rules out many uncontrolled factors like damping and inertia effects. Without the concern of the dynamic effects, it is also less complicated to derive geometrical models that are in more realistic shapes such as spherical shell or ellipsoidal membrane. All the static models we will look at either assumed spherical or ellipsoidal shapes.
The Orssengo-Pye Algorithm [21]: The formulae by Orssengo & Pye [21] was based on the deformation of the partial spherical shell under uniformly distributed load. They used the uniformly distributed load to represent the pressure exerted by the applanation indenter. Assuming small perturbation on the intraocular pressure, one can apply the principle of superposition to sum up the effects of the indentation pressure (IOPG, the measured value of the Goldmann applanation tonometer) which caused the inward deformation and the effect of the internal true intraocular pressure (IOPT) that pushed the cornea outward. Using the deformation formulae for partial spherical shell, the resultant deflection, 5, could be expressed as

where R was the radius of curvature of the anterior cornea, t was the center cornea thickness, E was the Young's modulus, A was the applanation area, vwas the Poisson’s ratio which was set to constant equal to 0.5 in this case, and a was a constant of corneal geometry determined also by shell deformation formulae. The formula was basically in the form of E = B . IOPG - C . IOPT with

both are material and geometry related constants. It was at this point when the author had to search for some typical experimental conditions when the IOPG would be equal to the IOPT. They referred to these typical cases were referred to them as the corneal calibration thickness, *c , and the corneal calibration radius of curvature, R . The two formulae then combined to yield the estimation for the true intraocular pressure as  s
s

Notice that with the IOPT and the IOPG been the same, the expression for the Young's modulus became

It could be seen that the critical point for this approach is the establishment of the "calibration cornea.” Some researchers used the mean of the test group to establish these "calibration dimensions” and used the values from the individual subjects for the "test cornea [20]”.
Later researches compared their modelling result with the finite element model simulation showed good correlation [20]. The model was easy to implement and had received wide popularity [24-26]. Although the advancement of computer modeling now gradually replaced its importance in correcting the IOPG, the last equation still offers an in vivo determination of the corneal Young's modulus.
The Sjøntoft-Edmund Model [22]: This is a very ancient model, but is theoretically very rigorous. The Sjøntoft-Edmund approach is based on the work-energy principle. They adopted the axisymmetric ellipsoidal shape for the cornea. When the cornea was at steady-state, it would assume a minimum potential energy configuration. As the cornea was indented, the work done by the indenting pressure to deform the cornea would be equal to the change in the potential energy. From the force balance under the geometrical configuration, the authors were able to link the intraocular pressure to the geometrical parameters, the eccentricity , and ageometrically measurable parameter, . Based on these force balanced relationship and the stress-strain relationship, the authors were able to derive an expression for the potential energy in terms of the Young's modulus, , and the Poisson's ratio was again set to 0.5 in this case. The potential energy to maintain the shape of the cornea was

and the volume of the cornea was
 where t = t0 = αx2 was used to represent the varying cornea thickness. And the volume bounded by the frontal plane through limbus and the corneal surface would be
where t = t0 = αx2 was used to represent the varying cornea thickness. And the volume bounded by the frontal plane through limbus and the corneal surface would be

Assume the volume bounded by the limbus plane and the corneal surface would maintain constant, one could obtain a relationship between the change in e and the change in PG. From the work- energy principle, one could also write IOP. ΔW = ΔU . Because ΔW remains zero, one can first calculate a change in pg with respect to a given small Δe as

Also, the equilibrium condition Δwork = IOP . ΔW = ΔU would hold if a correct Young's modulus was in place. This then enabled an iteration procedure to calculate the correct Young's modulus.
Notice that the authors also made a few additional assumptions:
The cornea was with layered structure but only the stroma was strong enough to hold the membrane resistance.
1. There was a linear load-deformation relationship of the cornea.
2. The hydration of the cornea maintained constant and the cornea material was incompressible.
3. The Young's modulus was constant over the entire cornea.
4. The cornea was axisymmetric in shape. The model is more involved to apply, therefore, it had not received many applications. Most citations had instead cited their assumptions [27,28] or their conclusion about inconsistent measurement results [29].
The Simplified Taber's Model [30]
For years people have been investigating the relationship between the force and the deformation of spherical objects [31,32]. The Taber’s model [33,34] proposed in 1982 was based on the perturbation method. Consider the cornea as a fluid filled spherical shell, the force equilibrium was established among the external applied force, the internal fluid pressure, and the shell stiffness force. There were also assumptions on the geometry of the cornea was a portion of the hemisphere; the material properties were homogeneous, isotropic, and with uniform thickness; all geometric and material properties were constants; the fluid was incompressible; the edge of the corneal hemisphere was clamped to the limbus; the corneal deflection at the moment of applanation could be regarded as static.
The total energy included the energy from the edge bending load, , the energy associated with the stretching and compression of the outer and inner shell, , respectively, and the work done by the external load,  L.
L.

In addition, the system was under the constraint that there was no change of volume,  which was achieved by amending a Lagrange multiplier, P. The total potential energy of the system was then
which was achieved by amending a Lagrange multiplier, P. The total potential energy of the system was then

with the participating parameters been: ,
,  , the inner and outer shell displacements,p the normalized fluid pressure, y1 the normalized moment term, y2 the horizontal force term,y3 the shell rotation term, and y4 the horizontal shall displacement term. The equilibrium condition required that the partial derivative of the total potential energy,π , with respect to all these participating parameters should all be zero, which led to a set of five simultaneous equations. This set of equations was still too hard to solve. One therefore reasonably set the shell rotation term y3 and the horizontal shell displacement term y4 to zero because the deflection induced by the external force was much larger than that was induced by the internal pressure and the bending moment. This led to the relationship
, the inner and outer shell displacements,p the normalized fluid pressure, y1 the normalized moment term, y2 the horizontal force term,y3 the shell rotation term, and y4 the horizontal shall displacement term. The equilibrium condition required that the partial derivative of the total potential energy,π , with respect to all these participating parameters should all be zero, which led to a set of five simultaneous equations. This set of equations was still too hard to solve. One therefore reasonably set the shell rotation term y3 and the horizontal shell displacement term y4 to zero because the deflection induced by the external force was much larger than that was induced by the internal pressure and the bending moment. This led to the relationship

an the resulting simplified Taber's model became:

These three equations then combined to give a simplified relationship between the vertical deflection of the cornea apex Δ (or  and
and  ) and the external pressure (the applied force). The biomechanical properties such as the Young's modulus and the Poisson’s ratio were both embedded within the coefficients. It was then possible to deduce these properties, the Young's modulus, in particular, through the measurement data. The formulae were simple. It was possible to perform the extraction in vivo. The application of the tests on 536 patients reported an average Young's modulus of 0.32 MPa.
) and the external pressure (the applied force). The biomechanical properties such as the Young's modulus and the Poisson’s ratio were both embedded within the coefficients. It was then possible to deduce these properties, the Young's modulus, in particular, through the measurement data. The formulae were simple. It was possible to perform the extraction in vivo. The application of the tests on 536 patients reported an average Young's modulus of 0.32 MPa.
The Dynamic Corneal Biomechanical Model
The dynamic corneal model could be more involved, but due to their time domain nature most proposed models used comparatively simple elements. Single degree of freedom models and two-degree of freedom models have been developed [35-37]. To exhibit the combined elastic and hysteresis effect, Glass et al. [37] used a three-component spring and dashpot model and compare it with the high-speed camera recordings [37]. They were able to compare the modeling results to the corneal phantom experiments and to discuss the effect of the different parameters. Notice that the quantitative parameters presented by the models were not adequate for clinical evaluation. The important clinical indicators like central corneal thickness was not involved [38]. It was not totally convincing to use the simple lumped block mass to represent the curved cornea diaphragm.
In addition, there is also limitation on the applicable instruments. Instead of just examining the corneal deformation, the dynamic models fit the time domain response of the model to the test data. The IOP instruments that can be used with this approach are then limited to the ones that offer dynamic responses in addition to the IOP and geometrical parameters. As discussed before, the Ocular Response Analyzer (ORA) [6] is one that records the response of the cornea apex. The Corvis ST [5], with the high-speed Scheimpflug imaging, can be viewed as an advanced ORA which also allows the observation of the cornea motion. Although it has been used mainly for IOP measurement, people are exploring better use of the image data.
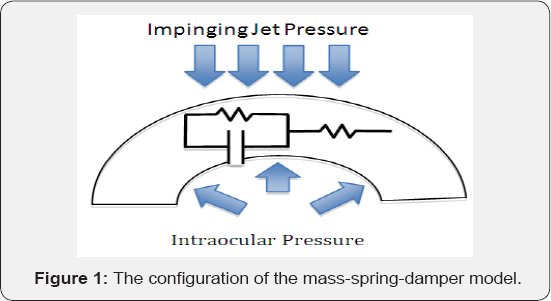
The Spring-Mass-Damper Model: The lumped models tried to capture the corneal dynamic behavior by capturing the movement of the center of the corneal. The basic concept is as show in Figure 1.
There were possibilities of different arrangements of the elements to reflect different corneal dynamic characteristics. Glass et al. [37] proposed the arrangement in Figure 1 to represent the reaction to the force generated in the lamellae and to exhibit the elongation response to the tensile force within the lamellae. All the derivation were carried out along the peripheral dimension. The main objective of Glass's model was on the response to the sinusoidal excitation. The hysteresis in terms of the ORA notation was evaluated through the differences in the peak stresses, the viscosity, and the elasticity. Although they did not stress on the evaluation of the Young's modulus, this approach showed potential in the in vivo applications.
The configuration adopted in Kaneko et al. [35], on the other hand, was perpendicular to the limbus surface to represent the cornea reaction to the impinging jet force, Figure 2. This model was focused on describing the cornea movement from the jet thrust. The authors calibrated their setup against some artificial eyeball for validation; however, the relationship between the spring constant and the Young's modulus or the relationship between the damping ration against the cornea hysteresis were not specified. Nor did they establish the material properties of the artificial eye against normal human eye.
Free Vibration Model with Resonance Frequencies
In 2015, Shih et al. [39] demonstrated another corneal dynamic model using the fluid filled sphere configuration [39]. This model first established the fundamental spherical wave function for a spherical cornea model. One could then fit these fundamental functions to the measurement response to determine the corresponding phase and magnitude of each function. The biomechanical material properties could then be extracted from the coefficients.
The simplifying assumptions includes:
1. The eyeball was part of a perfectly spherical diaphragm, and the fluid was completely filled;
2. The thickness and material of the diaphragm were uniform everywhere;
3. The amplitude of oscillation was small;
4. The fluid was incompressible water;
5. The iris was neglected;
6. The impinging air pressure assumes a Gaussian distribution;
7. Boundary conditions at the surface outside the eyeball are free [40-42]. The modeling procedure was separated into three parts: the air outside the eyeball, the diaphragm of the eyeball, and the fluid inside the eyeball.
For the outside air and the fluid inside the eyeball, the Euler's equation was in governance.

where 𝒱t was the covariant component of velocity fields, ρ is the density, p is the pressure, and neglect the fluid viscosity. With the appropriate boundary conditions, the solution of the pressure distribution, both inside and outside of the eyeball, was found to be functions of time in terms of the angular frequency, «, the eyeball radius, r, the constant amplitude coefficients A1m+ for the outside air, A1m- for the inside fluid (l and m were the indices for the harmonic orders), and the spherical surface harmonics function, Y1m [42].
The stretched diaphragm used the modified Helmholtz equation [43].

where E is the Young's modulus, T is the tension on the diaphragm, t is the diaphragm thickness, 𝒱 is the Poisson's ratio, ρ is the density of the diaphragm, and [p] is the pressure difference between the two sides of the diaphragm, i.e. [p] = p+ - p-;
With the solutions to the air, diaphragm, and liquid ofthe model, the more involved the modeling procedure was in establishing the continuity between the interfaces. Assuming continuity on both the displacement and the velocity of the interfaces, one could obtain a relation among the amplitude coefficients of the wave bases. Using this relation to substitute the amplitude coefficients, one obtained the modal equation in the form of

One could now write the series expansion expression for the variable 𝒲lm by the spherical harmonic surface function, Ylm . Taking the condition that the impinging force was axisymmetric so that the lateral expansion, m, became zero, the solution for the displacement could now be derived to be:

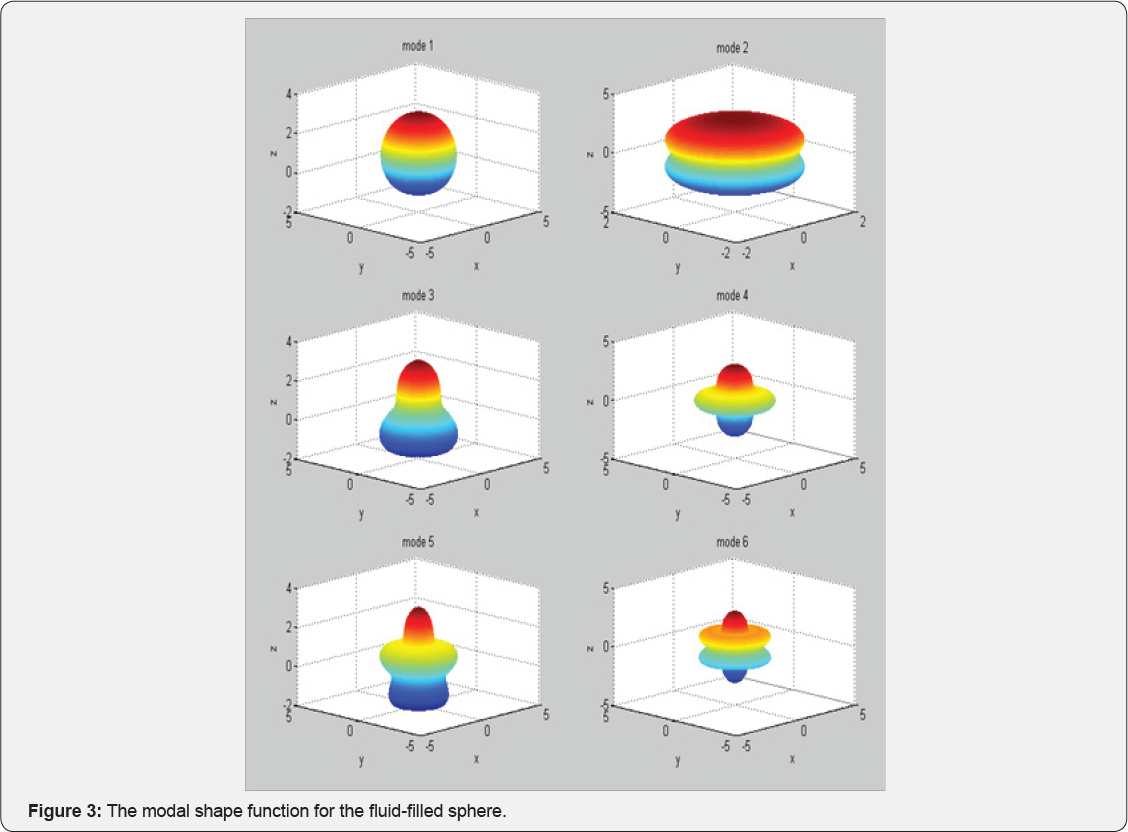
Shih et al. [39] calculated the modal shape function as in Figure 3.
One could then use these modal shape functions to fit the measurement response, and extract the material properties, including the Young’s modulus, from the coefficients. The fitting required an iterative process, and could potentially consume computer time. But with the current progress in the processor computing power, it would not be too difficult to embed the algorithm and perform the estimation in vivo.
Using this model, the authors extracted the corneal Young's modulus from 25 patients with their Young's modulus ranging from 0.0103 to 1.2427 MPa. The range was large, but they were in agreement with the previous studies [19,20,44-46].
Conclusion
It is not feasible to perform direct corneal Young's modulus measurement on human subjects. Therefore, people had to resolve to the extraction of the Young's modulus through the available test data. The process often involved comparing the test data with the response of an underlining model. According to the physical principle adopted, the models could be static models or dynamic models. The static models do not consider the inertia and the viscosity effect, thus they tend to allow more realistic but complicated geometric description. Many static models assumed the spherical or elliptical corneal shape and the outcome were the corneal deformation under foreign actions. The dynamic models, on the other hand, took advantage of the time series data available from most modern IOP measuring instruments, but they tend to depend on the lumped models that cannot express the geometrical effects. One recent dynamic model was able to derive the response of the fluid-fill sphere for the corneal geometry, but the deduction of the Young’s modulus requires iteration process. Most of the biomechanical models provided estimations that were in agreement with the literature, and all the ones reviewed showed potential for in vivo implementations.
Acknowledgement
The authors wish to thank the Ministry of Science and Technologies, Taiwan for the financial support under contract No.104-2221-E-002 -077 -MY3.
References
- Ljubimova D (2009) Biomechanics of the human eye and intraocular pressure measurements [Ph.D.]. KTH Royal Institute of Technology, Sweden.
- Herndon LW (2006) Measuring intraocular pressure-adjustments for corneal thickness and new technologies. Curr Opin Ophthalmol 17(2): 115-119.
- Shah S (2000) Accurate intraocular pressure measurement - The myth of modern ophthalmology? Ophthalmology 107(10): 1805-1087.
- Gaddie B, Bloomenstein M, Timons J, Wooldridge R (2012) Using biomechanics to advance glaucoma care. Reichert Technologies, USA, pp. 1-12.
- Hong J, Xu J, Wei A, Deng SX, Cui X, et al. (2013) A new tonometer- the Corvis ST tonometer: clinical comparison with noncontact and Goldmann applanation tonometers. Invest Ophthalmol Vis Sci 54(1): 659-665.
- Realini T (2008) The Ocular Response Analyzer. Glaucoma Today. p. 4.
- Kouchaki B, Hashemi H, Yekta A, Khabazkhoob M (2017) Comparison of current tonometry techniques in measurement of intraocular pressure. J Curr Ophthalmol 29(2): 92-97.
- Stephenson M (2011) Can you trust your IOP readings?
- De Moraes CVG, Hill V, Tello C, Liebmann JM, Ritch R (2012) Lower corneal hysteresis is associated with more rapid glaucomatous visual field progression. J Glaucoma 21(4): 209-213.
- Gatzioufas Z, Labiris G, Stachs O, Hovakimyan M, Schnaidt A, et al. (2013) Biomechanical profile of the cornea in primary congenital glaucoma. Acta Ophthalmologica 91(1): e29-e34.
- Garcia-Porta N, Fernandes P, Queiros A, Salgado-Borges J, Parafita-Mato M, et al. (2014) Corneal biomechanical properties in different ocular conditions and new measurement techniques. ISRN Ophthalmol 2014: 724546.
- Piñero DP, Alcon N (2015) Corneal biomechanics: A review. Clin Exp Optom 98(2): 107-116.
- He X, Liu J (2011) Correlation of corneal acoustic and elastic properties in a canine eye model. Invest Ophthalmol Vis Sci 52(2): 731-736.
- Hollman KW, Shtein RM, Tripathy S, Kim K (2013) Using an ultrasound elasticity microscope to map three-dimensional strain in a porcine cornea. Ultrasound Med Biol 39(8): 1451-1459.
- Alonso-Caneiro D, Karnowski K, Kaluzny BJ, Kowalczyk A, Wojtkowski M (2011) Assessment of corneal dynamics with high-speed swept source Optical Coherence Tomography combined with an air puff system. Opt Express 19(15): 14188-14199.
- Scarcelli G, Yun SH (2010) Brillouin microscopy for ocular biomechanics. Lasers and Electro-Optics/Quantum Electronics and Laser Science Conference.
- Last JA, Liliensiek SJ, Nealey PF, Murphy CJ (2009) Determining the mechanical properties of human corneal basement membranes with atomic force microscopy. J Struct Biol 167(1): 19-24.
- Knox Cartwright NE, Tyrer JR, Marshall J (2011) Age-Related Differences in the Elasticity of the Human Cornea. Invest Ophthalmol Vis Sci 52(7): 4324-4329.
- Wang HC, Prendiville PL, McDonnell PJ, Chang WV (1996) An ultrasonic technique for the measurement of the elastic moduli of human cornea. Journal of Biomechanics 29(12): 1633-1636.
- Hamilton KE, Pye DC (2008) Young’s modulus in normal corners and the effect on applanation tonometry. Optom Vis Sci 85(6): 445-450.
- Orssengo GJ, Pye DC. Determination of the true intraocular pressure and modulus of elasticity of the human cornea in vivo. Bull Math Biol 61(3): 551-572.
- Sjøntoft E, Edmund C (1987) In vivo determination of young's modulus for the human cornea. Bull Math Biol 49(2): 217-232.
- Goldmann Applanation Tonometer.
- Śródka W (2013) Applanation pressure function in Goldmann tonometry and its correction. Acta Bioeng Biomech 15(3): 97-106.
- Elsheikh A, Wang D, Kotecha A, Brown M, Garway-Heath D (2006) Evaluation of goldmann applanation tonometry using a nonlinear finite element ocular model. Ann Biomed Eng 34(10): 1628-1640.
- Liu J, Roberts CJ (2005) Influence of corneal biomechanical properties on intraocular pressure measurement: Quantitative analysis. J Cataract Refract Surg 31(1): 146-155.
- Hjortdal JØ (1996) Regional elastic performance of the human cornea. J Biomech 29(7): 931-942.
- Śródka W, Iskander DR (2008) Optically inspired biomechanical model of the human eyeball. J Biomed Opt 13(4): 044034.
- Zhang J, Zhang Y, Li Y, Chen R, Shung KK, et al. (2017) Correlation of IOP with Corneal Acoustic Impedance in Porcine Eye Model. Biomed Res Int.
- Shih PJ, Hung CJ, Huang TH, Lin HC, Yen JY, et al. (2017) Estimation of the Corneal Young's Modulus In Vivo Based on a Fluid-Filled Spherical- Shell Model with Scheimpflug Imaging. Journal of Ophthalmology 2017: 5410143.
- Sabir AB (1964) Large Deflection and Buckling Behaviour of a Spherical Shell with Inward Point Load and Uniform External Pressure. Journal of Mechanical Engineering Science 6(4): 11.
- Steele CR, Skogh J (1970) Slope discontinuities in pressure vessels. Journal of Applied Mechanics, Transactions ASME 7(3): 587-595.
- Taber LA (1982) Large Deflection Of A Fluid-Filled Spherical-Shell Under A Point Load. Journal of Applied Mechanics-Transactions of the Asme 49(1): 121-128.
- Taber LA (1983) Compression Of Fluid-Filled Spherical-Shells By Rigid Indenters. Journal of Applied Mechanics-Transactions of the Asme 50(4A): 717-722.
- Kaneko M, Tokuda K, Kawahara T (2005) Dynamic sensing of human eye. IEEE International Conference on Robotics and Automation.
- Von Freyberg A, Sorg M, Fuhrmann M, Kreiner CF, Pfannkuche J, et al. (2009) Acoustic tonometry: Feasibility study of a new principle of intraocular pressure measurement. J Glaucoma 18(4): 316-320.
- Glass DH, Roberts CJ, Litsky AS, Weber PA (2008) A viscoelastic biomechanical model of the cornea describing the effect of viscosity and elasticity on hysteresis. Invest Ophthalmol Vis Sci 49(9): 39193926.
- Kaushik S, Pandav SS (2007) Measuring Intraocular Pressure: How Important is the Central Corneal Thickness? Journal of Current Glaucoma Practice 1(1): 21-24.
- Shih PJ, Cao HJ, Huang CJ, Wang IJ, Shih WP, et al. (2015) A corneal elastic dynamic model derived from Scheimpflug imaging technology. Ophthalmic Physiol Opt 35(6): 663-672.
- Śródka W (2006) Effect of kinematic boundary conditions on optical and biomechanical behaviour of eyeball model. Acta of Bioengineering and Biomechanics 8(2): 69-77.
- Coquart L, Depeursinge C, Curnier A, Ohayon R (1992) A fluid-structure interaction problem in biomechanics: Prestressed vibrations of the eye by the finite element method. J Biomech 25(10): 1105-1118.
- Grinfeld P (2012) Small oscillations of a soap bubble. Studies in Applied Mathematics 128(1): 30-39.
- Strutt JW, Rayleigh B (1877) The Theory of Sound. MacMillan and Co, London, UK, pp. 325.
- Jue B, Maurice DM (1986) The mechanical properties of the rabbit and human cornea. J Biomech 19(10): 847-853.
- Elsheikh A, Alhasso D, Rama P (2008) Biomechanical properties of human and porcine corneas. Exp Eye Res 86(5): 783-790.
- Elsheikh A, Wang D, Pye D (2007) Determination of the modulus of elasticity of the human cornea. J Refract Surg 23(8): 808-818.