Introduction

Glioblastoma multiforme (GBM) is a deadly type of type of brain cancer that results in death within 1.5 years of diagnosis. There has been a lot of theoretical work that deal with optimal strategies to control this devastating disease. Many models have been developed describing the dynamic interactions between the cancer cells and the various treatments used to destoy the cancerous cells. The dynamics of this interaction is highly complex and nonlinear. Bifurcation analysis has been used by several workers to understand this complexity. Additionally, rigorous optimal control procedures have been used to maximize the elimination of the cancer cells while minimizing the costs involved. The aim of this work is to perform multiobjective nonlinear model predictive control in conjunction with bifurcation analysis on full and truncated models with and without the various protein complexes that are involved.

Background

Xu & co-workers [1] developed a novel strategy to overcome drug resistance associated with mitochondrial respiratory defect and hypoxia. Kaufman et al. [2] demonstrated the Glioma expansion in collagen matrices: analyzing collagen concentration-dependent growth and motility patterns. Farin et al. [3] developed a dynamic analysis showing that transplanted glioma cells migrate and proliferate on host brain vasculature: a dynamic analysis.

Furnari et al. [4] discussed genetics, biology, and paths to treatment for malignant astrocytic glioma. Stein & co-workers [5] developed a mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment. Beadle & co-workers [6] discussed the role of myosin II in glioma invasion of the brain. Godlewski et al [7] showed that targeting of the BMI-1 oncogene/stem cell renewal factor by microRNA-128 inhibits glioma proliferation and self-renewal. Kim et al. [8] demonstrated that epidermal growth factor-induced enhancement of glioblastoma cell migration in 3D arises from an intrinsic increase in speed but an extrinsic matrix and proteolysis-dependent increase in persistence.

Sen et al. [9] discussed isoform-specific contributions of a-cctinin to glioma cell mechanobiology. Kim & co-workers [10] developed a mathematical model of Brain tumor: pattern formation of glioma cells outside the tumor spheroid core. Godlewski & co-workers [11] developed a conditional switch controlling glioma cell proliferation and migration. Godlewski et al. [12] showed that mircroRNA-451 regulates LKB1/AMPK signaling and allows glioma cells to adapt to metabolic stress. Kim et al. [13] developed a mathematical model describing miR451 and AMPK Mutual Antagonism in Glioma Cell Migration and Proliferation.

Wesseling et al. [14] discuss the pathological diagnosis of diffuse gliomas: towards a smart synthesis of microscopic and molecular information in a multidisciplinary context. Kim [15] described the regulation of cells considering proliferation and migration in Glioblastoma using a therapeutic strategy. Kim & Roh [16] developed a hybrid model describing cell proliferation and migration in glioblastoma. Dhruv et al. [17] showed that the reciprocal activation of transcription factors underlies the dichotomy between the proliferation and invasion of glioma cells. Pyonteck et al. [18] concluded that the inhibition alters macrophage polarization and blocks glioma progression. Xie et al. [19] provided an overview of proliferation and invasion targeting adaptive glioblastoma. Lamszus et al. [20] discussed links between cellular function, glucose metabolism, and the glioma microenvironment. Kim et al. [21] developed strategies for eradicating Glioma Cells using a Multi-Scale Mathematical Model with miR-451-AMPK-mTOR control.

De los Reyes et al. [22] developed optimal control strategies of eradicating invisible glioblastoma cells after conventional surgery. Han et al. [23] investigated TGF-beta signaling and its targeting for glioma treatment. Goodwin & co-workers [24] researched Extraneural Glioblastoma Multiforme Vertebral Metastasis. Duzgun et al [25] discussed the role of mTOR in glioblastoma while Lee et al (2017)[26] studied the the role of myosin II in glioma invasion. Rajesh & co-workers [27] studied glioma progression through the prism of heat shock protein mediated extracellular matrix epithelial to mesenchymal transition. Kim et al. [28] investigated the role of extracellular matrix and microenvironment in regulation of tumor growth and LAR-mediated invasion in glioblastoma. Esmaeili et al. [29] the Direction of Tumour Growth in Glioblastoma Patients. Krol et al. [30] were able to detect circulating tumour cell clusters in human glioblastoma. Jung et al. [31] developed strategies in regulating glioblastoma signaling pathways and anti-invasion therapy.

In this work, the model described in Jung et al. [31] is used and multiobjective nonlinear model predictive control in conjunction with bifurcation analysis on full and truncated models with and without the various protein complexes. The model equations are first described. Then the numerical strategies for bifurcation analysis and multiobjective nonlinear model predictive control procedures are presented followed by the results and discussion and conclusions.

Model Equations

Gval represents the glucose that regulates Mval, the miR-451 (M). Aval represents AMPK, and Rval is the mTOR with the signaling pathway to cell cycle dynamics. Dval represents the drug that suppresses the inhibition of mTOR by AMPK. CyCB and Cdh1 represent the Cyclin B complex and the APC-Cadherin 1 complex.

The active form of the p55cdc-Anaphase-promoting complex is represented by [p55cdcA], and the total p55cdc-Anaphase-promoting complex is [p55cdcT]. The active form of Polo-like kinase 1 protein is [Plk1] and the cell mass is represented by [mass]. [ mass_s] is the pseudo mass given by

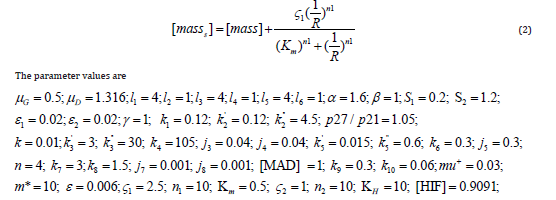
These parameters represent glucose consumption rate, drug decay rate, miR-451 autocatalytic production rate, Hill-type coefficient AMPK autocatalytic production rate, Hill-type coefficient, AMPK autocatalytic production rate, Hill-type coefficient, inhibition strength of miR-451 by AMPK complex, inhibition strength of AMPK complex by miR-451, signalling source of AMPK, signalling source of mTOR, scaling factor (slow dynamics) of AMPK complex, scaling factor (slow dynamics) of mTOR, inhibition strength of AMPK complex by miR-451 , production rate of [CycB] , the degradation rate of [CycB] , the degradation rate of [CycB] by [Cdh1] inhibitory effect of p21 or p27 genes, oxygen concentration threshold, activation rate of [Cdh1] , the activation rate of [Cdh1] by [p55cdcA] , inactivation rate of [Cdh1] by [CycB] , Michaelis-Menten activation constant, Michaelis-Menten inactivation constant, production rate of [p55cdcT] transcription rate of [p55cdcT] by [CycB], the degradation rate of [p55cdcT] , the dissociation constant of [p55cdcT] , Hill coefficient, activation rate of [p55cdcA], inactivation rate of [p55cdcA] , Michaelis-Menten activation constant, Michaelis-Menten inactivation constant, spindle checkpoint genes concentration, the activation rate of [Plk1] by [CycB], the degradation rate of [Plk1], specific growth rate, maximum size to which a cell may grow, cell cycle heterogeneity growth rate parameter, Hill-type parameter, Hill-type parameter, Hill-type parameter, Hill-type parameter, Hill-type parameter, Hill-type parameter , and the Hypoxia-inducible factor

are both bifurcation parameters and control values.

Bifurcation Analysis

The existence of multiple steady-states and limit cycles in various processes has led to much research involving bifurcation analysis. Multiple steady states occur because of the existence of branch and limit points. Hopf bifurcation points cause limit cycles. One of the most commonly used software to locate limit points, branch points, and Hopf bifurcation points is the MATLAB program MATCONT [32,33]. This software detects Limit points (LP), branch points (BP), and Hopf bifurcation points(H). Consider an ODE system

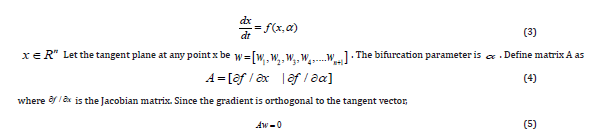
Multiobjective Nonlinear Model Predictive Control

Results and Discussion

The original model has eleven ordinary differential equations (Eq. 1) . Since the first 5 equations of this model were self-sufficient (the other variables are not present in the first five equations ) the truncated model was first considered. The effects of the chemical protein comlexes were not considered. The model equations for the truncated model are

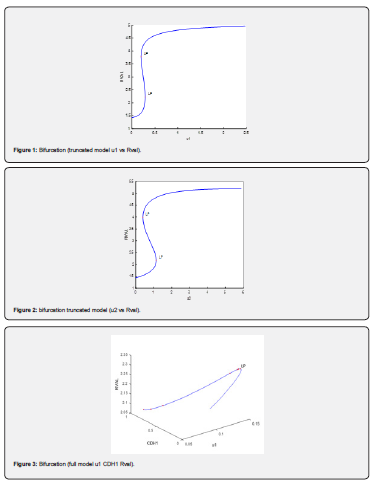
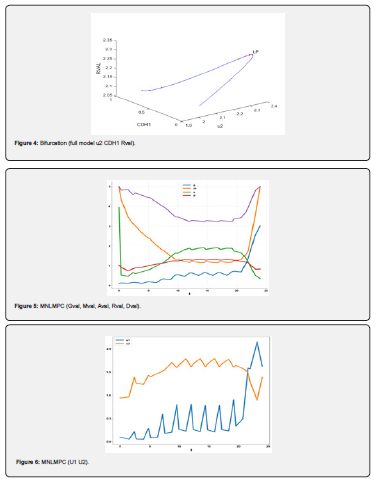
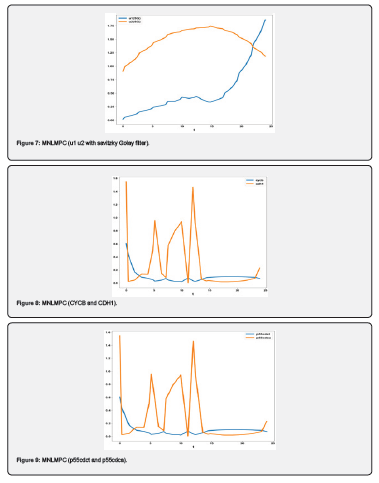
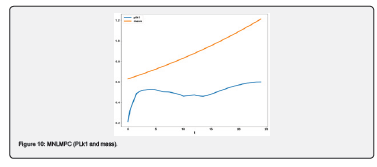
Conclusion

Multiobjective nonlinear model predictive control in conjunction with bifurcation analysis on the truncated and full models without and with various protein complexes. The bifurcation analysis reveals the existence of limit points. These limit points cause the Lagrangian multipliers in the multiobjective nonlinear model predictive control calculations to go to 0 yielding the utopia solution. Additionally, for the MNLMPC calculations, both the truncated and full models gave identical answers confirming that the Lagrangian multipliers were 0 for both the models.

Acknowledgement

Dr. Sridhar thanks Dr. Carlos Ramirez and Dr. David Suleiman for their encouragement

References

1. Xu RH, Pelicano H, Zhou Y, Carew JS, Feng L, et al. (2005) Inhibition of glycolysis in cancer cells: a novel strategy to overcome drug resistance associated with mitochondrial respiratory defect and hypoxia. Cancer Res 65(2): 613-621.
2. Kaufman LJ, Brangwynne CP, Kasza KE, Filippidi E, Gordon VD, et al. (2005) Glioma expansion in collagen I matrices: analyzing collagen concentration-dependent growth and motility patterns. Biophys J BioFAST 89: 635-650.
3. Farin A, Suzuki SO, Weiker M, Goldman JE, Bruce JN, et al. (2006) Transplanted glioma cells migrate and proliferate on host brain vasculature: a dynamic analysis. Glia 53(8): 799-808.
4. Furnari FB, Fenton T, Bachoo RM, Mukasa A, Stommel JM, et al. (2007) Malignant astrocytic glioma: genetics, biology, and paths to treatment. Genes Dev 21(21): 2683-2710.
5. Stein AM, Demuth T, Mobley D, Berens M, Sander LM (2007) A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro Biophys J 92(1): 356-365.
6. Beadle C, Assanah MC, Monzo P, Vallee R, Rosenfield SS, et al. (2008) The role of myosin II in glioma invasion of the brain. Mol Biol Cell 19(8): 3357-3368.
7. Godlewski J, Nowicki MO, Bronisz A, Williams S, Otsuki A, et al. (2008) Targeting of the BMI-1 oncogene/stem cell renewal factor by microRNA-128 inhibits glioma proliferation and self-renewal. Cancer Res 68(22): 9125-9130.
8. Kim HD, Guo TW, Wu AP, Wells A, Gertler FB, et al. (2008) Epidermal growth factor-induced enhancement of glioblastoma cell migration in 3D arises from an intrinsic increase in speed but an extrinsic matrix and proteolysis-dependent increase in persistence. Mol Biol Cell 19(10): 4249-4259.
9. Sen S, Dong M, Kumar S (2009) Isoform-specific contributions of alpha-actinin to glioma cell mechanobiology. PLoS One 4(12): e8427.
10. Kim Y, Lawler S, Nowicki MO, Chiocca EA, Friedman A (2009) A mathematical model of Brain tumor: pattern formation of glioma cells outside the tumor spheroid core. J Theor Biol 260(3): 359-371.
11. Godlewski J, Bronisz A, Nowicki MO, Chiocca EA, Lawler S (2010) MicroRNA-451: A conditional switch controlling glioma cell proliferation and migration. Cell Cycle 9(14): 2742-2748.
12. Godlewski J, Nowicki MO, Bronisz A, Palatini GNJ, Lay MD, et al. (2010) MircroRNA-451 regulates LKB1/AMPK signaling and allows adaptation to metabolic stress in glioma cells. Molecular Cell 37: 620-632.
13. Kim Y, Roh S, Lawler S, Friedman A (2011) miR451 and AMPK Mutual Antagonism in Glioma Cell Migration and Proliferation: A Mathematical Model. PLoS One 6(12): 1-10.
14. Wesseling P, Kros JM, Jeuken JWM (2011) The pathological diagnosis of diffuse gliomas: towards a smart synthesis of microscopic and molecular information in a multidisciplinary context. Diagnostic Histopathology 17(11): 486-494.
15. Kim Y (2013) Regulation of Cell Proliferation and Migration in Glioblastoma: New Therapeutic Approach. Frontiers in Oncology 3: 53.
16. Kim Y, Roh S (2013) A hybrid model for cell proliferation and migration in glioblastoma. Discrete & Continuous Dynamical Systems—B 18(4): 969-1015.
17. Dhruv HD, Winslow WSM, Armstrong B, Tuncali S, Eschbacher J, et al. (2013) Reciprocal activation of transcription factors underlies the dichotomy between proliferation and invasion of glioma cells. PLoS One 8(8): e72134.
18. Pyonteck SM, Akkari L, Schuhmacher AJ, Bowman RL, Sevenich L, et al. (2013) CSF-1R inhibition alters macrophage polarization and blocks glioma progression. Nat Med 19(10): 1264-1272.
19. Xie Q, Mittal S, Berens ME (2014) Targeting adaptive glioblastoma: an overview of proliferation and invasion. Neuro Oncol 16(12): 1575-1584.
20. Lamszus K, Kathagen A, Holz M, Schulte A, Westphal M (2014) Go or grow—links between cellular function, glucose metabolism and glioma microenvironment. NeuroOncol 16(Suppl 3): iii6.
21. Kim Y, Powathil G, Kang H, Trucu D, Kim H, et al. (2015) Strategies of Eradicating Glioma Cells: A Multi-Scale Mathematical Model with MiR-451-AMPK-mTOR Control. PLoS One 10(1): e0114370.
22. de los Reyes V AA, Jung E, Kim Y (2015) Optimal control strategies of eradicating invisible glioblastoma cells after conventional surgery. Journal of The Royal Society Interface 12(106).
23. Han J, Alvarez-Breckenridge CA, Wang QE, Yu J (2015) TGF-beta signaling and its targeting for glioma treatment. Am J Cancer Res 5(3): 945-955.
24. Goodwin CR, Liang L, Abu-Bonsrah N, Hdeib A, Elder BD, et al. (2016) Extraneural Glioblastoma Multiforme Vertebral Metastasis. World Neurosurg 89: 578-582.
25. Duzgun Z, Eroglu Z, Avci CB (2016) Role of mTOR in glioblastoma. Gene 575(2 Pt 1): 187-190.
26. Lee W, Lim S, Kim Y (2017) The role of myosin II in glioma invasion: A mathematical model. PLoS One 12(2): e0171312.
27. Rajesh Y, Biswas A, Mandal M (2017) Glioma progression through the prism of heat shock protein mediated extracellular matrix remodeling and epithelial to mesenchymal transition. Exp Cell Res 359(2): 299-311.
28. Kim Y, Kang H, Powathil G, Kim H, Trucu D, et al. (2018) Role of extracellular matrix and microenvironment in regulation of tumor growth and LAR-mediated invasion in glioblastoma. PLoS One 13(10):1-40.
29. Esmaeili M, Stensjoen AL, Berntsen EM, Solheim O, Reinertsen I (2018) The Direction of Tumour Growth in Glioblastoma Patients. Sci Rep 8(1): 1199.
30. Krol I, Castro-Giner F, Maurer M, Gkountela S, Szczerba BM, et al. (2018) Detection of circulating tumour cell clusters in human glioblastoma. Br J Cancer 119(4): 487-491.
31. Jung E, de los Reyes V AA, Pumares KJA, Kim Y (2019) Strategies in regulating glioblastoma signaling pathways and anti-invasion therapy. PLoS ONE 14(4): e0215547.
32. Dhooge A, Govearts W, Kuznetsov AY (2003) MATCONT: A Matlab package for numerical bifurcation analysis of ODEs. ACM Transactions on Mathematical Software 29(2): 141-164.
33. Dhooge A, W Govaerts, YA Kuznetsov, W Mestrom, AM Riet (2004) CL_MATCONT; A continuation toolbox in Matlab.
34. Kuznetsov YA (1998) Elements of applied bifurcation t Springer, NY, USA.
35. Kuznetsov YA (2009) Five lectures on numerical bifurcation analysis, Utrecht University, NL.
36. Govaerts WJF (2000) Numerical Methods for Bifurcations of Dynamical Equilibria, SIAM.
37. Flores-Tlacuahuac, A Pilar Morales, Martin Riveral Toledo (2012) Multiobjective Nonlinear model predictive control of a class of chemical reactors. I & EC research, pp. 5891-5899.
38. Hart WE, Laird CD, Watson JP, Woodruff DL, Bynum ML, et al. (2017) Pyomo – Optimization Modeling in Python. (2^nd edn), Vol. 67. Springer.
39. Wächter A, Biegler L (2006) On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 106: 25-57.
40. Tawarmalani M, NV Sahinidis (2005) A polyhedral branch-and-cut approach to global optimization. Mathematical Programming 103(2): 225-249.
41. Sridhar LN (2024a) Coupling Bifurcation Analysis and Multiobjective Nonlinear Model Predictive Control. Austin Chem Eng 11(1): 1107.
42. Upreti SR (2016) Optimal control for chemical engineers. Taylor and Francis, p. 305.