Abstract

EDXRF technique has been used to measure L XRF cross-sections of elements Ba & La at 12 KeV excitation energy using synchrotron radiations. A Peltier cooled Vortex solid state detector (SII Nano Technology, USA) with an energy resolution of 138 eV at 5.96 KeV X-rays was employed for the present analysis. Theoretical L XRF cross sections are measured using two different models-Dirac-Hartree-Slater (DHS) and Dirac-Fock (DF). Two major peaks ()Lii, αβ=and one minor peak ()Liil=are analysed for their cross-sections. The experimental and theoretical results of LXRF cross sections are compared. Measured results of cross-sections are found in good agreement with calculated values with DHF and DF models. Earlier some different excitation sources like X-ray tube or radioactive sources were employed by many authors to measure LXRF cross-sections. Barium is important element and can be used to analyze the major elements in silicate rock samples. Lanthanum is also abundant element in nature LXRF results will became very helpful for calculating the quantitative measurements in its available ore samples. Along with LXRF cross-sections, elemental concentration of gold sample has been also measured as an application of EDXRF which may play an important role in the field of forensic science. Three main constituents Au, Cu and Ag were found in major concentration with amount of 90.138, 6.799 and 2.881% respectively. Traces of Ni were also observed during analysis. EDXRF technique also facilitates the process of identification of unknown forensic metal samples which have been mishandled.

Keywords: EDXRF; L XRF Cross Section; Si (Li) detector; Elemental analysis; Synchrotron radiation; Forensic science

Abbreviation: EDXRF: Energy Dispersive X-ray Fluorescence; XRF: X-ray Fluorescence; DHS: Dirac-Hartree-Slater; DF: Dirac-Fock; BIS: Bureau of Indian Standards

Introduction

Energy dispersive X-ray fluorescence (EDXRF) is one of the significant techniques that have been broadly used for qualitative as well as quantitative nondestructive multi-elemental analysis in a number of disciplines i.e. geology, biology, forensic science, petroleum, environmental science, medicines, atomic and nuclear phenomenon etc. This technique is based on the ionization of the atoms of the material being investigated by an energetic beam of primary X-rays. The characteristic radiation that is emitted by the ionized atoms upon relaxation contains information on the nature of the constituent elements present. The energy of each X-ray peak in spectrum is associated with the presence of a particular element and the intensity of the peak (area under the photo peak) is related to the elemental concentration. The emission of characteristic atomic X-ray photons occurs when a vacancy in an inner electron state is formed and an outer shell electron makes a transition to that vacant state. Understanding the nature and origin of characteristic X-ray line spectrum requires the knowledge of atomic structure. The precise measurement of LX-ray fluorescence (XRF) cross section plays a very significant role in the basic and applied studies of nuclear and atomic physics involving photoionisation cross-sections, fluorescence yields, fractional X-ray emission rates and Coster-Kronig transitions etc.

Various analysis of forensic interest is also become possible with EDXRF technique. This technique has been widely used in applications like art conservation and in archaeology, to analyse modern coloured glasses, analysis of Indian nail polish, analysis of paints flakes, analysis of coins, fly ash sample study, ayurvedic drugs study and in several forensic science investigations.

Various authors [1-9] measured L X-ray fluorescence cross section of many elements at different excitation energies with DHS and DF models. Earlier our group [10-11] measured L-XRF cross section of W and Ba, La, Ce at different excitation energies. On the other hand, EDXRF technique can also be used for a tremendous variety of elemental analysis of forensic interest like paint flakes, gold samples, coin analysis etc. [12-15]. In the present work, the L XRF cross-sections for the element Ba and La have been measured with excitation energy of 12 keV using synchrotron radiations. Present paper also reports on non-destructive EDXRF analysis as an application for assaying of gold content in given gold sample (may be fake/undercarat/genuine) like bangle, ring, necklace etc. Excitation sources like X-ray tubes and radioactive sources are used by most of the authors. Present works also focus on utilization of synchrotron-based analysis of the samples.

The experimental results of Cross-sections have been also compared with the theoretical estimates calculated with the fluorescence yield and Coster-Kronig transition probability of Puri et al. [16] and Campbell [17]. Two different X-ray emission rates-based models, Dirac-Hartree-Slater (DHS) by Scofield [18] and Dirac-Fock (DF) [19] reported by Campbell and Wang, were also used here. The results present the new set of experimental data of above said elements with synchrotron radiations and also help in explaining inner shell ionization processes using various theoretical models. Measured results also show reliability of DF model-based X-ray emission rates for accurate measurement of XRF cross sections. EDXRF technique has been used here to find the major and minor concentration of gold sample which may be useful in forensic science.

Method of Measurement

Present investigations have been carried out at Raja Ramanna Centre for Advanced Technology (RRCAT), Indore [using Microprobe-XRF beam line (BL-16), Indus –II Synchrotron]. A pictorial view of the synchrotron radiation setup is shown in Figure 1, described elsewhere [12] and briefly explained here.
i. The microprobe XRF beamline (BL-16) has been installed on the 5th port of a bending magnet. It has been designed to work in the photon energy range 4-20 keV and has an acceptance of 1 mrad (Horizontal)× 0.2 mrad (Vertical).
ii. The main optical components of the beamline include a fixed-exit double-crystal monochromator (DCM) (FMB, Berlin, Germany) with a pair of symmetric and asymmetric Si (111) crystals (mounted side-by-side) and a Kirkpatrick-Baez (KB) focusing optics (Xradia, USA) comprises of a pair of Platinum coated elliptical bendable mirror.
iii. The selection of asymmetric Si (111) crystals provides 1.5 to 2 times higher photon flux compared with symmetric Si (111) crystals. The geometrical setup consists of the sample that is kept at 45o to the incident beam in the horizontal deviation geometry. The fluorescent radiation was detected at 90o with respect to the incident beam by using a Peltier cooled Vortex solid state detector (SII Nano Technology, USA) with energy resolution of 138eV at 5.96keV X-rays.
iv. The beamline radiation shielding hutch and the builtin personal safety interlock system allow safe operation of the beamline. Detuning of the second crystal of DCM system with an intensity reduction of 50% for the first order harmonics was applied for the elimination of contribution of higher order energy contamination in the collimated monochromatic X-ray incident beam. Synchrotron X-rays at 12 keV were monochromatized using DCM and then employed for the sample excitation.

X-ray fluorescence (XRF) is most established modern analytical technique and has been widely used for elemental analysis and assaying purposes. Presently RRCAT beam lines facilities has been also used to measure concentration of gold ring sample of 22 carat.

Experimental Measurement

L XRF cross-section

The experimental L_i(i=l,α,β) XRF cross-sections of Ba and La were evaluated using the following relation:

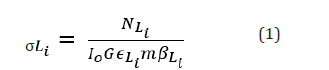
Here N_Li is the number of counts per unit time under photo peak corresponding to L_i group of X-rays of the element, I_o is the intensity of incident radiation, G is the geometrical factor, ε_Li is the detector efficiency for the L_i group of X-rays, m is the mass per unit area of the elements and β_Li is the self-absorption correction factor.

The values of self-absorption correction factor β_Li have been calculated by using the following expression, assuming that the fluorescence X-rays are incident normally at the detector.

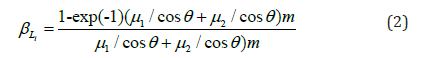
Here μ₁ and μ₂ are the mass attenuation coefficients corresponding to the incident and emitted X-ray energies respectively taken from the online data from XCOM [20] and θ is angle of incidence of emitted characteristic X-rays on the target and m is the mass thickness of target in mg/cm². The product 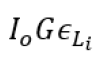contains the terms related to the incident flux, geometrical factor and the efficiency of the X-ray detector.

We can measure I_oGε_Li by using the relation

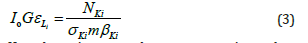
Here the various terms have same meaning as those mentioned in Eq. (1), except σ_Ki , that is the K_i X-ray production cross section of target, which is calculated using the following relation

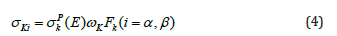
Here σ^p_k (E) is the K shell photoionisation cross-sections reported by Scofield [21] for the given element at the excitation energy E. ω_K and F_k are the K- shell fluorescence yield reported by Krause [22] and fractional X-ray emission rates for K_β,α X-rays reported by Scofield [18]. By using these data, an efficiency curve has been obtained between I_oGε_Li and characteristic X-ray energies as shown in Figure 2.

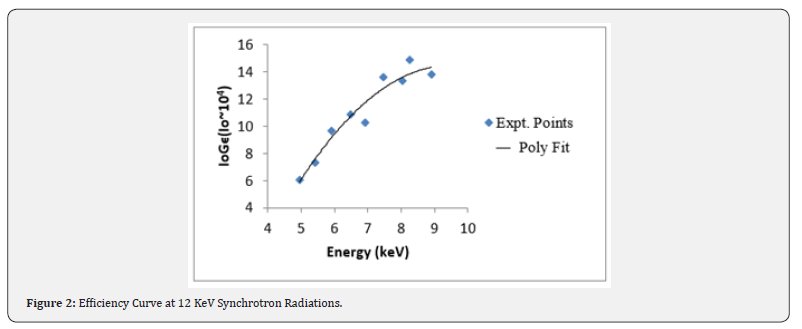
Atomic transitions correspond to different lines are as follows:

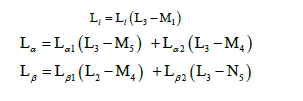
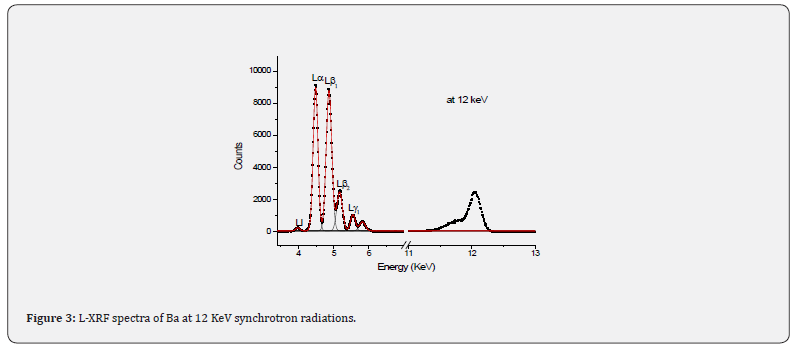
By using a constant function for the background radiation and Gaussian function, various L X-ray peaks were fitted and analysed by using software Origin Pro 8.5. Typical L XRF spectra for Ba at 12KeV with synchrotron radiations is shown in Figure 3.

Elemental concentration of the gold sample

The auto computer generated program with the instrument was used to measure the elemental concentration of the gold sample by using the following relation:

All the parameters are same as defined in Eqn (1).

The gold ring of 22 carat as shown in Figure 4 is used as sample whose elemental concentration has been find out here. The acquisition time for each sample analysis was ~100 seconds.

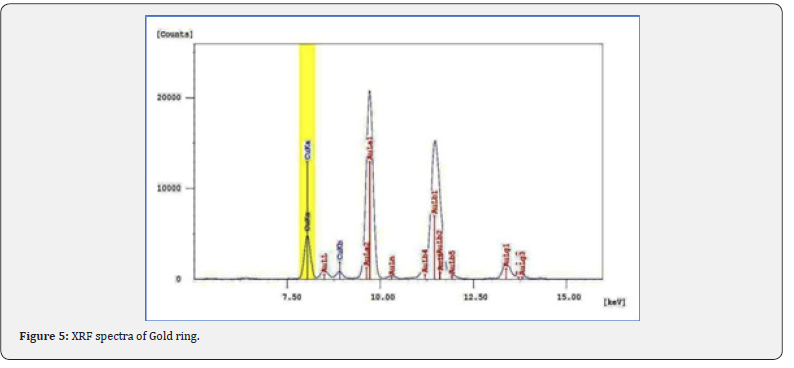
The XRF spectra of gold ring is shown in Figure 5.

For the analysis of gold jewelry items, the certified X-ray reference materials data [23] taken from Bureau of Indian Standards (BIS) IS-1417 and IS3095 were used as standards. For different cartages like 24, 23, 22, 18 etc., the gold contents are shown in Table 1.

These reference standard data were certified by BIS for gold and gold alloys, jewelry artifacts etc. BIS as National Body of India is primarily engaged in the preparation and promotion of standards and operation of different quality certification schemes.

Theoretical and Standard Results

Theoretical L XRF cross-sections

Theoretical values of the L_i(i= l,α,β) X-ray fluorescence cross- sections at the given excitation energy has been calculated using the following relations:

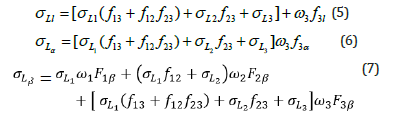
where σ_L1 σ_{L2 and σL3 are the subshell photoionization crosssections of the elements at given excitation energy taken from the standard data table [21]; ω1,ω2 and ω3 are the L-subshell fluorescence yields and f12,f13 and f23 are the Coster-kronig transition probabilities. Two different sets of ωi and fij were taken for theoretical calculation of L XRF cross- sections. First set is the interpolated predictions of the Dirac-Hartree-Slater version of the independent particle model by Campbell [17] with recommended values from Chen et al. [24] and LLNL (Lawrence Livermore National Laboratory) [25]. The second set is taken from the data based on the Relativistic Dirac-Hartree-Slater (RDHS) model given by Puri et al. [16]. Fnk(F3l,F3α,F1β,F2β,F3,F1γ,F2) are the fractions of the radiative transition probabilities of the subshells L1, L2 and L3 contained in the Kth spectral line. For example F3α is the fraction of the L X-rays originating from the L3 , transitions that contribute to the Lα peak.}

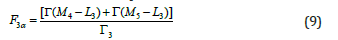
where F_3α is the sum of the radiative transition rate which contribute to the Lα line associated with the hole filling in the L₃ subshell, Γ_r is the theoretical total radiative transition rate of the L subshell, Γ(M₄ − L₃ ) is the radiative transition rate from the M₄ shell to the L₃ shell and Γ(M₅ − L₃) is the radiative transition rate from the M5 shell to the L₃ shell. The radiative transition rate has been calculated by using Dirac-Hartree-Slater (DHS) model [18] and assuming the same potential for the initial and final states of the atom undergoing the transition. The secondly, Dirac-Fock (DF) model [19] was used, which employed different initial and final atomic Hamiltonians, for which each wave function was built from the relevant single-particle wave functions. All other F_nx are similarly defined.

Standard elemental concentration of gold samples

For different cartages like 24, 23, 22, 18 etc., the gold contents are shown in Table 1.

For the authenticity of results, 22 carat standard gold sample has been also analysed with the same technique under same conditions. The 24 carat gold has a fineness of 999 and having 99.9% gold and known is the purest form of gold. The 24 carat gold having fineness of 995 with 99.5 % gold concentration is known as the standard gold. It is only used for standardization purposes and for gold artifacts, it is generally not used. The 22 carat gold contains 22 parts of gold and 2 parts of other metals. It has 916.7 fineness, or 91.67% pure gold.

Results and Discussion

The values of the L X-ray fluorescence cross- sections, as listed in Table 2, has been calculated from the theoretical subshell photoionisation cross- sections [21] and two different sets of fluorescence yields ω_i and Coster-Kronig transitions probabilities f_ij [16,17]. The yield values provided by Puri et al. [16] were the logarithmic interpolated values of radiative and nonradiative rates and make available a complete set of fluorescence and Coster-Kronig (CK) yields based on the ab initio relativistic Dirac-Hartree-Slater (DHS) model by considering the onset and cutoff of the different CK transitions [24]. However, Campbell [17] used a simple approach of interpolating in the ratio of the various yields reported by Chen et al. [24] and LLNL (Lawrence Livermore National Laboratory) reported by Perkin et al. [25]. In general, the values of L_i(i= l,α,β) fluorescence cross- sections calculated with the data of Puri et al. [16] are higher than those reported with Campbell [17] (approx. variation of 4-7%) due to variation in the values of Coster-Kronig transition probabilities.

However, uncertainties in the various tabulated parameters like photoionisation cross section, fluorescence yields, Coster- Kronig transition probabilities and fractional X-ray emission rates introduce error in the L XRF fluorescence cross-sections. The theoretical values of L XRF cross sections have been calculated by using both, the above said tabulated fluorescence yields and Coster-Kronig transitions probabilities [16,17] for Ba and La. The experimental L XRF cross sections based on two set of parameters i.e. fluorescence yields ω_i and Coster- Kronig transitions probabilities f_ij [16,17] with two different set of models i.e. DHS [18] and DF [19], are measured at excitation energy 12 KeV.

For major intense peaks, i.e. L_α, their XRF cross sections were found close to the theoretical results obtained with the help of physical parameters with maximum percentage error of ~ 1.9- 2.1% for DHS (Campbell) and 2.6-3.1% DF (Puri) model. For other major intense peaks, i.e.L_β(L_β1+L_β2) the XRF cross sections were found close to the theoretical results obtained with the help of physical parameters with maximum percentage error of < 1% for both DHS (Campbell) and DF (Puri) model.

However, for minor L_l peak, XRF cross sections observed a larger deviation of ~10.8-11.9% for DHS (Campbell) and 11.4- 12.8% for DF (Puri) model, being a least intense peak and having poor detection efficiency. The uncertainties in the experimental L XRF cross- sections values were determined by the propagation of errors in various physical parameters in Eqn (1) and estimated to be <1% in area under the L X-ray peaks, <2% in mass absorption correction factor, <2% in target mass thickness and <1% in the I_o G product.

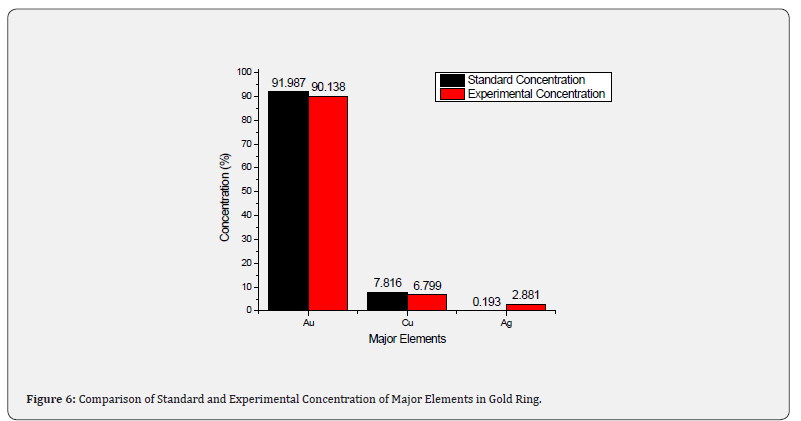
The gold sample i.e. gold ring has been analysed with EDXRF technique and results are shown in Table 1. Three main constituents Au, Cu and Ag were found in major concentration with amount of 90.138, 6.799 and 2.881% respectively. Besides this, traces of Ni are also observed during analysis. For the authenticity of the present results, BIS 22 carat gold sample was also analysed and Au, Cu and Ag were observed as 91.987, 7.816 and 0.193% respectively. Figure 6 illustrates the comparative presentation of major elements in gold ring sample.

Conclusion

In the present study, DHS and DF models were used to measure L XRF cross section using physical parameters of Puri et al. [16] and Campbell [17]. Most of the L_i(i=l,α,β) cross sections were found close to the theoretical values calculated with DF model based emission rates. In case of most intense L_i(i=α,β) peaks, results were observed in good agreement with the calculated data. As L_l peak is less intense peak, so poor counting statistics contribute a larger variation towards the experimental measurements as compared to the theoretical values.

For the first time, we have reported L XRF cross section for Ba and La with the monoenergetic synchrotron source at excitation energy of 12 keV. Synchrotron radiations are much better and stronger than other types of sources like X-ray tubes, radioactive sources. Earlier some different excitation sources like X-ray tube or radioactive sources were employed by many authors at various excitation energies to measure L XRF cross-sections of these elements. Barium and Lanthanum are important element in nature and present XRF results will became very helpful for calculating the quantitative measurements in its available ore samples. The present experimental data with synchrotron radiation at given energy of 12keV is not available in the literature. It also needs some more experimental data in order to establish a good comparison between theoretical and experiment results.

XRF analytical observations are also very important in forensic research, especially in criminal cases where metal samples such as gold have been mishandled. With this technique, samples of forensic interest can be easily examined and analyzed without introducing any foreign material into the sample. Present study demonstrates the effectiveness of the technique to analyze gold jewelry and suggests a way to avoid undervaluing gold jewelry. One main advantage of EDXRF technique that pays special attention to everyone is its non-destructive nature which means there is no amendment of the sample taken. XRF method also makes possible the process of recognition of unknown forensic sample.

Acknowledgement

This work was carried out by Microprobe-XRF beam line (BL- 16), Indus-II Synchrotron facilities at Raja Ramanna Centre for Advanced Technology (RRCAT), Indore (India). Authors are gratefully acknowledged to Dr. M.K. Tiwari (Head, X-Ray Optics Section, RRCAT, Indore) for providing the necessary experimental facilities to carry out this work.

References

1. DV Rao, R Cesareo, GE Gigante (1996) Ll, Lα, Lβ and Lγ X-Ray Fluorescence Cross-sections for Ce, Pr and Sm Excited by Y and Mo Kα X-Ray Photons. X-Ray Spectrom 25(2): 74-77.
2. A Kaya, M Ertugrul, O Dogan, O Sogut, U Turgut, et al. (2001) Measurement of L subshell X-ray fluorescence cross-sections at 59.54 keV and L subshell fluorescence yields for elements in the atomic range 55 ≤ Z ≤ Anal Chi Acta 441: 317-323.
3. W Salah, J Al-Jundi (2005) Measurement of L X-ray cross-sections and relative intensities of heavy elements by 15.2 keV photons. J Quant Spectrosc Radiat Transf 94: 325-333.
4. AC Mandal, S Santra, D Mitra, M Sarkar, D Bhattacharya (2005) L X-ray fluorescence cross sections of some rare earth elements (Z= 62, 64, 66, 68 and 70) at 17.8, 22.6 and 25.8 keV. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater Atoms 234: 176-184.
5. J Reyes Herrera, J Miranda (2016) Measurement of L_αand L_β1,3,4 fluorescence cross sections of La, Ce, Pr and Nd induced by photons of energies between 7.01keV and 8.75keV. Rad Phys Chem 123: 122-128.
6. RA Barrea, EV Bonzi (2001) Rare earth experimental L X‐ray fluorescence cross‐sections at 13 and 14 keV with synchrotron radiation. X-Ray Spectrom 30: 3-7.
7. R Kumar A, Rani RM, Singh MK, Tiwari AK, Singh (2016) Measurement of L-XRF cross-sections and Coster–Kronig enhancement factors for ⁶²Sm at excitation energies 6.8, 7.4 and 8KeV. J Electron Spectrosc. Relat Phenom 209: 34-39.
8. H Bansal, MK Tiwari, Raj Mittal (2017) L sub-shell fluorescence cross-section measurements for elements, Z = 62–67 at tuned photon energies. J Quant Spectrosc Radiat Transf 199: 93-102.
9. S Puri (2015) Theoretical X-ray production cross sections at incident photon energies across L_i(i=1-3) absorption edges of Br. AIP Conference Proceedings 1675(1): 030089.
10. R Kumar, A Rani, RM Singh, MK Tiwari, AK Singh (2017) Measurement of L X-ray fluorescence cross-sections for ⁷⁴W at excitation energies 12, 14, 15 and 16.5 keV with synchrotron radiation. Rad Phys Chem 131: 79-85.
11. R Kumar, A Rani, RM Singh, MK Tiwari (2019) L X-ray fluorescence cross-sections measurements for elements Ba, La and Ce at synchrotron radiation energies 7, 8, 9 and 10 keV. Rad Phys Chem 156: 283-291.
12. TR Rautray, B Behera, T Badapanda, V Vijayan, S Panigrahi (2009) Trace element analysis of fly ash samples by EDXRF technique. Indian J Phys 83(4): 543-546.
13. D Kloos (2003) Underkarat Jewelry: The Perfect Crime? Investigations And Analysis of Jewelry Using XRF. Advances in X-ray Analysis 46: 25-30.
14. A Rani, R Kumar (2019) Forensic Application of Energy Dispersive X-Ray Fluorescence to Analyse a Vehicle Paint Sample. J Forensic Sci & Criminal Inves 11(4): 555820.
15. Richa M, Kumari R Kumar, MK Tiwari (2024) Forensic Elemental Analysis of Five Rupee and One Pound Coin with EDXRF Technique. Am J Phys Appl 12(5): 104-111.
16. S Puri, D Mehta, B Chand, N Singh, PN Trehan (1993) L-shell fluorescence yields and Coster–Kronig transition-probabilities for the elements with 25≤Z≤ X-Ray Spectrum 22: 358-361.
17. JL Campbell (2003) Fluorescence yields and Coster–Kronig probabilities for the atomic L sub shells. At Data Nucl Data Tables 85: 291-315.
18. JH Scofield (1974) Relativistic Hartree-Slater values for K and L X-ray emission rates. At Data Nucl Data Tables 14: 121-137.
19. JL Campbell, JX Wang (1989) Interpolated Dirac-Fock values of L-subshell X-ray emission rates including overlap and exchange effects. At Data Nucl Data Tables 43: 281-291.
20. MJ Berger, JH Hubbell, SM Seltzer, J Chang, JS Coursey, et al. (2010) XCOM: Photon Cross-sections Database.
21. JH Scofield (1973) Theoretical Photoionization Cross Sections from 1 to 1500 keV. Lawrence Livermore National Laboratory Report UCRL-51326.
22. MO Krause (1979) Atomic radiative and radiationless yields for K and L shell. J Phys Chem Ref Data 8: 307-327.
23. Gold and Gold Alloys (2011) Jewellery/Artifacts-Fineness and Marking – Specification. Bureau of Indian standards, Doc: MTD 10(5076)W,4.
24. MH Chen, B Crasemann, K Huang, M Aoyagi, H Mark (1977) Theoretical L-shell Coster-Kronig energies. At Data Nucl Tables 19: 97-151.
25. ST Perkins, DE Cullen, MH Chen, JH Hubbell, J Rathkopf, et al. (1991) Tables and graphs of atomic subshell and relaxation data derived from the LLNL Evaluated Atomic Data Library (EADL), Z = 1--100. Lawrence Livermore National Laboratory Report UCRL-50400, 30.