Research Article

Hybrid Algorithm in Estimating Underwater Postmortem Interval: Idepis

Noor Maizura Mohamad Noor*, Amirul Harfirie Ahmad Nubli, Rosmayati Mohemad and Zuriana Abu Bakar

Universiti Malaysia Terengganu, Malaysia

Submission: June 09, 2018;Published: June 20, 2018

*Corresponding author: Noor Maizura Mohamad Noor, Universiti Malaysia Terengganu, School of Informatics and Applied Mathematics, 21030, Kuala Nerus, Terengganu, Malaysia, Email: maizura@umt.edu.my

How to cite this article: Noor M M N, Amirul H A N, Rosmayati M, Zuriana A B. Hybrid Algorithm in Estimating Underwater Postmortem Interval: Idepis. J Forensic Sci & Criminal Inves 2018; 9(4): 555768. DOI:10.19080/JFSCI.2018.09.555768.

Abstract

Crime investigation is a complex task, which involves huge amounts of information and requires many different types of expert knowledge. Estimation of the postmortem interval (PMI) is one of the most important aspects in forensic practice, mainly to assist in solving any crime investigation when the death has not been witnessed. Determination of the PMI is difficult with the progression of time and soft tissue decomposition, especially for underwater death. Underwater death investigation is challenging as the decomposition of body occurs more rapidly due to many contributing factors. This study aims to develop an enhanced decision-based system in estimating underwater PMI, known as iDepis. The main purpose of iDepis is to estimate the PMI underwater condition. Newton’s Law of cooling is usually used to estimate time of death but it is inaccurate to estimate PMI in underwater cases. With the combination of Henssge Nomogram, estimating the time of death could be ascertained by fixing the contributing factors. To make iDepis more reliable, stages of decomposition are integrated with the interval tree algorithm. Therefore, a combination of Newton’s Law of Cooling, Henssge Nomogram, and stages of decomposition will make the system’s decision reliable along with significant estimation of underwater postmortem interval.

Keywords: Corpse; Decision Support System; Postmortem Interval

Introduction

Over the past few decades, extensive work has been carried out to determine the Postmortem Interval (PMI) from changes in the biochemical constituents of various body fluids, such as blood, cerebrospinal fluid, and vitreous humor, immediately or shortly after death. PMI is known as the estimation of length of elapsed time since a person has died [1]. The goal of PMI is to determine the fact and subsequently identify the truth that can exonerate a suspect or focus suspicion on a suspect [2]. Accurate estimation of the PMI is a crucial and fundamental step in any crime investigation when the death has not been witnessed. However, the determination of PMI is difficult and becomes less accurate when the body has been immersed for a prolonged period of time especially in underwater deaths [3]. According to the statistics obtained from the World Health Organization and the Center for Disease Control and Prevention, the average of fatal drowning in the United States from 2005 to 2014 is 3,536 people annually [4,5].

Generally, to obtain the estimation time of underwater death either in a lake, river, ocean, or even in a bathtub is challenging as the decomposition of the body occurs more rapidly due to many contributing independent environmental factors such as temperature, bacterial content, salinity, and aquatic animal activity [6,7]. It becomes more challenging if the body has deceased somewhere else and then dragged into the water. Forensic science only works for truth by making sure the examination is complete, the test is performed correctly, the data is interpreted in-depth, and the report is written correctly and easily understood by non-scientists [8]. As of now, there is still a lack of accepted objective methods available that allows for reliable PMI estimation because usually PMI estimation is based on forensic expertise in which there is lack of standard procedure to estimate the time of death.

Thus, the objective of this study is to fill this gap by computerizing the PMI estimation whereby the system will generate the time of death by using a hybrid algorithm which is a combination of the Newton’s Law of Cooling, Henssge Nomogram, and stages of decomposition criteria. Therefore, it makes the results more reliable and significant for estimating the time of death. The remainder of this paper is organized as follows. Section 2 discusses the research background related to the estimation of time of death. Meanwhile, Section 3 explains the method that has been used to estimate the time of death in underwater cases. In Section 4, an architectural design and prototype of the system is presented. Subsequently, Section 5 discusses the experimental setup and result, where a comparison is made of results from the estimation of time of death using rabbit carcasses and the Decision Support System for Underwater Postmortem Interval System (iDepis) and finally, section 6 summarizes with a discussion and the conclusion.

Research Background

The following sub-sections provide a detailed background of this study including the Decision Support System (DSS), Postmortem Interval (PMI), fresh body, Algor Mortis, Rigor Mortis, Livor Mortis, and Adipocere.

Existing Algorithm

Asante had proposed a combination of algorithms between Newton’s Law of Cooling and Henssge Nomogram in estimating the time of death [9]. and the algorithm was improved by Muhammad [10]. However, the algorithm is not efficient in estimating the time of death in underwater cases due to changes in the contributing factors. It is because these factors cannot be controlled by humans such as the flowing of water, movement of surrounding air, humidity, and insect activity. The algorithm could be improved by integrating it with the stages of decomposition criteria generated from the interval tree algorithm. Stages of decomposition are mainly used by forensic experts to estimate the time of death in an underwater situation. This method is highly efficient because the physical changes of a corpse can be seen right away in a crime scene.

Postmortem Interval

The PMI, which is also known as the time since death estimation, aids forensic scientists in death investigations. In general, there are three (3) common methods typically used to predict PMI which are stages of decomposition, insect behavior and life cycles, and environmental factor [11]. PMI determination is a crucial procedure in forensic practice. Many factors affect the onset and the course of the PMI changes. Studies have shown that the ambient temperature, acidity/alkalinity, decomposition process, bacterial fermentation, and even oxygen pressure will influence the estimation of the PMI [11,12]. Among all factors, the ambient temperature is considered the most influential factor in PMI estimation. There have been increasing efforts in forensic practice to establish an accurate and objective method that can be applied in PMI estimation at the ambient temperature. Most researchers believe that as the cadaver is at a continuously variable ambient temperature, PMI evaluation of a single substance at a single temperature is not suitable for PMI estimation [12,13]. Multivariate approaches, such as generalized additive models (GAMs) or support vector machines (SVMs), allow various indicator substances to be incorporated into the model, thus improving the prediction of the PMIs.

Fresh Body

During this broad stage, at the time of death, the heart stops and the skin gets tight and gray. The cell starts to die (brain 3-7 minutes; skin up to 24 hours). The body muscle will relax, while the bladder and bowels will empty from the body.

Algor Mortis

Algor mortis refers to cooling of the body. In death, a body no longer generates warmth and begins to cool down. As such, temperature drop is used to estimate the time of death. Postmortem body temperature (TPM) declines progressively until it reaches the ambient temperature (TA). Metabolism generates heat (regulated to a narrow range). The body cools at a uniform rate, thus the rate of TPM decrease can be used to accurately determine the time of death [12]. However, body temperature is a narrow range, not a fixed temperature. The formula used is denoted in the methodology section under formulas 1 and 2.

Rigor Mortis

Rigor Mortis commonly refers to the stiffness after death [10,12]. Immediately after death, the body is limp due to the relaxation of the muscles. Muscles begin to stiffen due to the chemical changes in the muscle tissues. Muscles contract when myosin and acting stick together. Adenosine triphosphate (ATP) is needed to detach the two. The muscle will stay locked in a constant state of contraction without ATP (in death) and it cannot be separated. It occurs in all muscles simultaneously, but can sometimes be seen in smaller muscles first such as the face, jaw, neck, and then the trunk and other extremities. There are three (3) rules to determine the states of rigor mortis. First, within 10 hours of death, the muscle starts to stiffen. Second, the whole body will stiffen within 12 to 18 hours and the stiffness starts to disappear after about 24 hours. Thus, after 24 hours from the time of death, rigor mortis cannot be used to estimate the time of death.

Livor Mortis

Livor Mortis, which is also known as the discoloration of the body after death [12]. (Forensic Medicine for Medical Students, 2015), occurs due to the gravitational settling of the blood [8]. The blood starts to pull at the lower part of the body which causes the upper body discoloration and paleness. It begins thirty minutes up to three hours after death; the skin gets purple and waxy. Lips, fingers, and toenails become pale or turn white. Hands and feet turn blue. Eyes start to sink into the skull.

Adipocere

Adipocere is a skeleton decomposition. It usually takes 9 to 10 days or faster [8]. Commonly, the corpse is immersed in water or a pool. The water must be warm to ensure the fat undergoes the hydrolysis process. Based on the summary of the studies, five criteria have been adopted for application in the iDepis, which include fresh body, cooling of the body, and stiffness of muscle, discoloration, and adipocerous, as denoted in Table 1. In order to estimate the time of death of a corpse, all the criteria will be integrated with the interval tree algorithm.

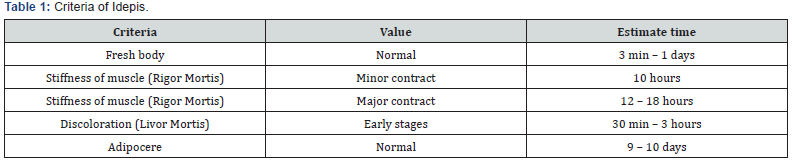
Materials and Methods

Henssge nomogram as illustrated in Figure 1. Is a method to fix the error in the estimation of time of death. It is also called the correcting factor. Henssge introduced two (2) nomograms which can calculate the estimated time of death with rectal temperature of up to 25℃ and down to 25℃. The estimated time of death and the correction factor are obtained by drawing a straight line from the ambient temperature and cross-lined with the rectal temperature. Therefore, the correcting factor in underwater cases has been selected as shown in Table 2. The Newton’s Law of Cooling was introduced by Sir Isaac Newton in 1701 The formula was originally used to calculate the rate of temperature change in the body. Later, forensic experts started using the formula to estimate the time of death. Therefore, the formula is used in this study as shown in the following:

= 37 − (℃) + 3 (1)

= 98.6 − (℃) (2)

1.5

Where: T = Time of death

Rt = Rectal temperature

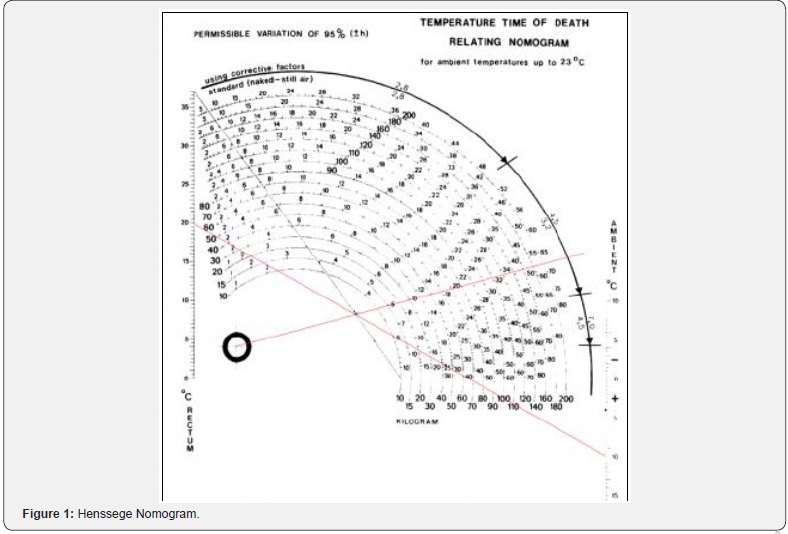
The algorithm used to derive the stages of decomposition criteria is the interval tree using the concept of binary search. Basically, an interval tree is a tree of data structure that holds the time intervals. It is efficient in finding all the intervals that overlap with any interval or point. In this case, the criterion of interval time has been used to determine the overlap time among the criteria [14]. as shown in Figure 2. he total hours of overlapping time will be the total estimation of the time of death. Samples of the algorithm (Geeks for Geeks, n.d.) and the java pseudo code are stated as follows.

Start

a. Sort the time interval in increasing order.

b. Push the first interval on to a stack

c. For each interval do the following

I. If the current interval does not overlap with the stack top, push it.

II. If the current interval overlaps with the stack top and ending time of the current interval is more than that of the stack top, update the stack top with the ending time of the current interval.

d. The end of the stack contains the merged intervals.

e. Get reliable time of death of merged intervals.

End

The selection process of overlapping time of death among the criteria executed in interval tree algorithm also can be illustrated in Figure 2. All of the selected criteria are arranged in ascending order. Then, the algorithm detects the overlapping time of death between the criteria. The worst-case criteria which are unreliable or not overlap will be removed from the algorithm. The best-case of overlapping criteria will be selected and the algorithm will select the time that most frequent overlap to each other. The full flow process hybrid algorithm execution is illustrated in the Figure 3.

Architecture Design & Prototype of the System

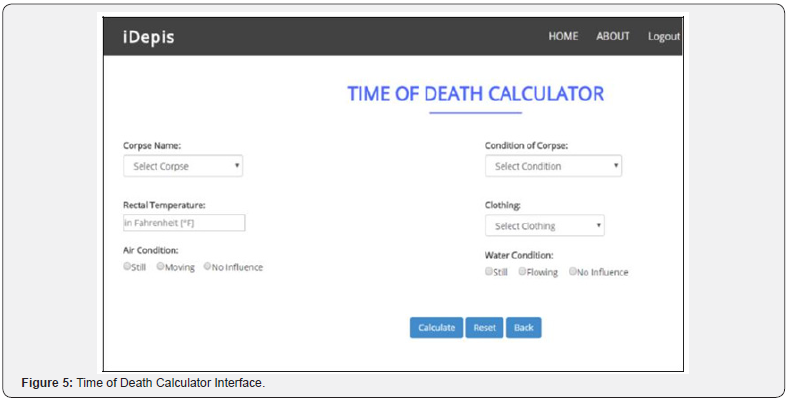
Figure 4 illustrates the architecture of the Decision Support System for the Underwater Postmortem Interval System (iDepis) that has been developed to estimate the time of death. The engine of this system includes criteria such as condition of air, condition of water, layer of clothing, condition of clothing, stiffness of corpse, discoloration of corpse, layer of corpse’s skins, and so on, used along with the interval tree algorithm. Next, these methods are used in combination with Newton’s Law of Cooling and Henssge Nomogram. The estimation of the time of death will be stored in the MySQL database and the analysis reports will be generated via the Java Server Page (JSP) Figure 5. Shows the screenshot of iDepis, which illustrates the iDepis calculator and form. The user can utilize this system by selecting the corpse that has been registered by the police. Then, the user has to fill in the rectal temperature field for the Newton’s Law of Cooling. Next, the user selects all the criteria needed from the crime scene and hits the submit button to generate the results and a full report. Meanwhile (Figure 6). Illustrates the yearly report that can be generated from selecting the current or past year. The system can generate yearly report by categorizing the cause of death.

Results

The following sub-sections discuss the details of the experiment, such as the experimental setup and results.

Experiment Setup

An experiment was conducted on 9 January 2017 to validate and compare the results of the iDepis with rabbit carcasses via animal etiquette. A science officer was hired to do an experiment with the standard animal procedure. Rabbit carcasses were chosen because the composition of their body is similar to the human body [15]. thus making the estimated time of death almost similar to human death. There were 6 samples of rabbit carcasses. Each of them was immersed in water under different types of conditions and criteria sets. However, there are still more criteria that we could not control such as surrounding air, water temperature, humidity, flow of water (damp and lake), and disturbance of animals.

Results

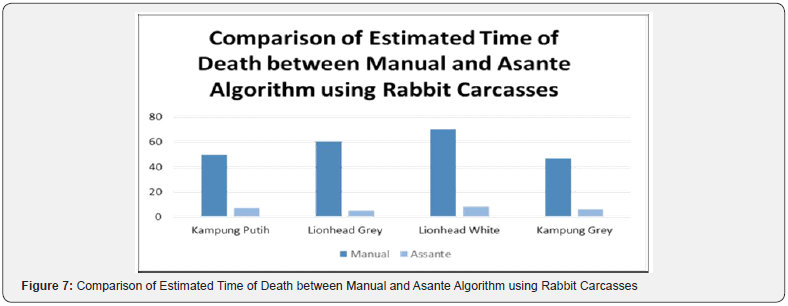
Figure 7 illustrates the comparison of results of the estimated time of death by using the Asante algorithm and the real underwater time of death. Figure 7 shows the comparison of results of the estimation of the time of death by using the Asante algorithm and the real underwater time of death against the types of rabbits. (Figure 8). illustrates the comparison of results of the estimated time of death by using iDepis and the real underwater time of death against the types of rabbits. From the illustration in Figures 7 & 8, Kampung Putih, Lionhead Grey, Lionhead White, and Kampung Grey represent the samples and types of rabbit carcasses. After the results for the time of death are recorded, the standard deviation is calculated [16,17]. This calculation is important to measure the dispersion that refers to a distribution’s extent of stretching between values in a set of data. The lower the standard deviation, the closer the data points tend to be the expected value, μ. Conversely, a higher standard deviation indicates a wider range of values.

Discussion

For the Asante algorithm, the standard deviation is calculated is 27.68 with mean (x̅ ) 31.67. Based on the results, the standard deviation shows the data have spread too much from the original time of death. Moreover, we can observe a huge gap in Figure 6 between the Asante Algorithm’s generated time of death and the rabbit carcasses’ time of death [18,19]. Next, the data set of rabbit carcasses and iDepis is used to calculate the standard deviation. The standard deviation for this sample data is 10.31. Based on the results of this experiment, the value of the standard deviation is not spread too much away from the mean (x̅ ), which is 53.75. Therefore, the data from the iDepis result is reliable for estimating the time of death for underwater cases.

Conclusion

Decision making on estimating time of death is important to determine the exact time the corpse deceases. The iDepis could assist the forensic analyst to obtain the estimation of the time of death efficiently in a short time. Decision makers in the forensic unit can calculate the estimation of the time of death based on a combination of algorithms such as the interval tree, Henssge Nomogram, and Newton’s Law of Cooling. Certain information about the corpse can be accessed without wasting a bundle of paper to store the statistics of the death as it can be automatically searched through the system by using the web browser. In the future, in order to improve decision-making, an artificial intelligent agent needs to be integrated with the iDepis to assist crime investigation. Furthermore, added features such as the back-tracking technique could be integrated with the artificial intelligent agent to improve the estimation of the time of death. To accomplish these tasks efficiently, a new framework or model should be designed, the algorithm should be improved, and the real data from the crime scenes should be employed. Finally, forensic experts must be involved in validating and verifying the system.

Acknowledgement

The authors would like to thank the Royal Police Malaysia (RPM) for its continuous support. This work is supported by a grant from the Fundamental Research Grant Scheme (FRGS) and the Ministry of Higher Education (MOHE) with the vot number 59432.

References

1. Sharma R, Kumar Garg R, Gaur JR (2015) Various methods for the estimation of the post mortem interval from Calliphoridae: A review Egypt J Forensic Sci 5(1) 1-12.
2. Lyle DP (2008) Time of Death: A Critical Part of the Timeline. Writer’s Digest.
3. Hobischak NR, Anderson GS (1999) Freshwater-Related Death Investigations in British Columbia in 1995–1996. A Review Of Coroners Cases. Can Soc Forensic Sci J 32(2-3): 97-106.
4. Lesson WLS (2012) Drowning Statistics.
5. (2015) WHO, World heath statistics 2015.
6. Alan Gunn (2006) The Decay Process in Essential Forensic Biology, Second edi. Liverpool: John Wiley & Sons.
7. Laura Ayers E (2010) Differential Decomposition in Terrestrial, Freshwater, and Saltwater Environments: A Pilot Study. Texas State University-San Marcos.
8. Saukko P, Knight B, Knight’s Forensic Pathology, Third edit. London: Edward Arnold Ltd.
9. Asante S (2013) Application of Newton ’ S Law of Cooling Case Study : Estimation of Time of Death in Murder. Kwame Nkrumah University of Science and Technology.
10. Abdullah MC, Noor NMM, Bakar ZA (2014) the Incorporation of Algorithm With Newton Law of Cooling As a Methodology To Estimate the Time of Death of Corpse or Cadaver p. 15-16.
11. Dix J, Graham M (1999) Time of Death, Decomposition and Identification.
12. DiMaio V J, DiMaio D (2001) Forensic Pathology Second edition.
13. Mao S, Fu G, Seese RR, Wang ZY ( 2013) Estimation of PMI depends on the changes in ATP and its degradation products. Leg Med 15(5): 235-238.
14. Brooks JW (2016) Postmortem Changes in Animal Carcasses and Estimation of the Postmortem Interval. Vet Pathol 53(5): 929-940.
15. Ismail SS, Bull ID, Evershed RP (2016) Interpreting Anthropogenic Signals From a Clandestine Grave Via Soil Lipid Biomolecular Analysis. Trans Sci Technol 3(3): 501-506.
16. Henssge C (1981) Temperature time of death relating nomogram.
17. Lewis MA (2010) The Physics of Inflation : Newton’s Law of Cooling and The consumer Price Index. J Appl Quant. Methods 5(1): 105-112.
18. Gatev G, Hossain A (2007) Interval Algorithms for Solving Minimal Spanning Tree and Shortest-Route Models. Inf Tecnol Control 4: 37-46.
19. Bakar ZA, Abdullah MC, Noor NMM (2018) Post-mortem Interval Estimation System (e-PMI) in Estimating the Time of Death. Int J Inf Educ Technol 8(1): 46-50.