Radiotherapy Lung Cancer Fractionated Biological Effective Dose Optimization with Genetic Algorithm Pareto-Multi objective Method - Part II
Francisco Casesnoves*
Independent Research Scientist & Independent Bioengineering Laboratory Director, International Association of Advanced Materials, Sweden. Uni science Global Scientific Member, Wyoming, USA
Submission: August 01, 2025; Published: August 22, 2025
*Corresponding author: Francisco Casesnoves, PhD Engineering, MSc Physics-Mathematics, Physician, Independent Research Scientist, Independent Bioengineering Laboratory Director, International Association of Advanced Materials, Sweden. Uni science Global Scientific Member, Wyoming, USA, Email: casesnoves.research.emailbox@gmail.com
How to cite this article: Francisco Casesnoves. Radiotherapy Lung Cancer Fractionated Biological Effective Dose Optimization with Genetic Algorithm Pareto-Multi objective Method - Part II. Int J Pul & Res Sci. 2025; 8(1): 555728.DOI: 10.19080/IJOPRS.2025.08.555728
Abstract
This contribution constitutes an advance from previous articles in Breast and Head and Neck cancer Radiotherapy BED modelling (Biological Effective Dose). Lung tumors Hyper fractionation TPO (Treatment Planning Optimization) is programmed with Pareto-Multi objective (PMO) Genetic Algorithms (GA) software. Artificial Intelligence methods (AI) with GA are applied on hyper fractionated TPO and detailed. Results comprise PMO-AI imaging process sequences and numerical values of PMO Lung cancer TPO parameters. Further results prove PMO-GA BED model both with Pareto-Optimal Front detailed graphics, charts, and numerical dose fractionation datasets. Solutions for improved and advanced RT Lung cancer TPO, and tumors in general for Fractional-dose photon dose delivery are explained. Mathematical Medical Physics analysis and a few numerical comparisons to previous published research for Breast and Head and Neck cancer PMO with Evolutionary Artificial Intelligence are presented.
Keywords:Pareto-multi objective optimization; Mathematical methods; Biological models; Radiation therapy; Initial tumor clonogenes number population; Effective tumor population clonogenic number; Linear quadratic model; Integral equation; Tumor control probability; Normal tissue complications probability; Biological effective model; Tumor control cumulative probability; Radiation photon-dose; Nonlinear optimization; Radiotherapy treatment planning optimization; Source-surface distance; Software engineering methods; Radiation photon-dose; Attenuation exponential factor; Nonlinear optimization; Radiotherapy wedge filter; Anisotropic analytic model; fluence factor; Omega factor; Treatment planning optimization; Breast tumor; Artificial intelligence; Pareto-multi objective optimization; Genetic algorithms
Abbreviations:PMO: Pareto-Multi objective Optimization; MM: Mathematical Methods, BM: Biological Models; RT: Radiation Therapy; LQM: Linear Quadratic Model; IE: Integral Equation; TCP: Tumor Control Probability; NTCP: Normal Tissue Complications Probability; BED: Biological Effective model, TCCP: Tumor Control Cumulative Probability, RPD: Radiation Photon-Dose; TPO: Treatment Planning Optimization; SSD: Source-Surface Distance; AEF: Attenuation Exponential Factor; WF: Wedge Filter; AAA: Anisotropic Analytic Model; FF: Fluence Factor, OF: Omega Factor; TPO: Treatment Planning Optimization; BT: Breast Tumor; AI: Artificial Intelligence; PMO: Pareto-Multi objective Optimization; GA: Genetic Algorithms
Introduction
Formerly, biological models BED-TPO simulations with AI-GA were proven in a series recent publication for Head and Neck and Breast tumors [1-23]. This article shows modelling advances from those methods/results towards one of the most epidemiologically frequent in male and female cancer patients actually, namely lung tumors. Artificial Intelligence with Genetic Algorithms in engineering software is applied on radiotherapy BED model for Lung cancer. The objective of this research is further development, programming, obtain two types of AI-GA 2D Graphics-numerical Optimization, and extensive dataset results for BED model hyper fractionated TPO protocol in Lung cancer [24]. Therefore, the focus of the study is getting accurate and software functionality optimization of BED model for lung cancer hyper fractionated RT treatment. Epidemiologically, the importance of lung cancer screening among smokers and individuals with risk factors, has been proven recently. The reason is that survival rate after 5 years among early-stage diagnosed lung tumors is significantly higher [25-38]. Surgical resection of lung tumors at stage I (T1–2, N0) NSCLC yields satisfying outcome results with 5-year survival rates of 60–70%, and remains at present the golden standard in this population. After resection, radiotherapy is optional.
Lung tumors are a heterogeneous type of cancer. Their incidence and prevalence are statistically among the highest percent of all tumors and constitute the highest deaths cancer rate at present. In general, [96], Non-Small-Cells-Lung carcinoma has a prevalence of approximately 85% of all lung tumors, while Small-Cells-Lung carcinoma shows about 15% of prevalence. In addition, lung and breast cancer show be the highest incidence in brain metastases [39-45]. For example, 234,000 Primary Lung cancer cases in USA in 2018 with 154,050 deaths. In 1990 the incidence peak was [70 / 100,000 population], in 2018 [57 / 100,000 population] . This specific decrease of incidence in that developed country is probably due to healthier population habits related to tobacco consumption and contact with other toxic substances/chemicals. The most important oncological causal factor for lung cancer is proven be tobacco consumption, even in passive smokers. However, further pathogenesis factors are mainly chemical, from the external media intake/contact. Namely, radon gas, passive smoking, prior radiation from any radiation source [39-40,46-80], inhaled chemicals (polycyclic aromatic hydrocarbons), heavy metal inhaled particles and/or micro-nano particles. Among previous diseases, for instance pulmonary fibrosis. If any potential patient is smoker and at the same time is in contact with carcinogenetic chemicals, the ontogenetic synergism factor increases the probability of lung cancer. Therefore, although the tobacco consumption is decreasing in developed countries, it does not happen so in underdeveloped ones. This has caused an incidence/prevalence social-geographic-pathology rate displacement towards those countries. In addition, when smoking, the oral cavity can accumulate tobacco and alcohol as ontogenetical factors. This pathogenesis can cause concomitant diseases associated to the main lung tumor [81].
The radiosensitivity of tumor cells for optimal RT treatment has two main factors to be considered [82-109], namely, alpha and Betha coefficients and repopulation (Tumor Cells Intrinsic Radiosensitivity). From about 4 days after dose fraction irradiation, the fraction of clonogenic increases almost exponentially. Intrinsic radio sensibility is a crucial factor for Biological Effective Dose because the model depends on alpha and betha coefficients. The mathematical reason is that the exponential for survival fraction for radiobiological models is modified by these important parameters (Algorithm 2), [23]. According to [109], the alpha values vary [0.72,0.52], and the beta one’s change [0.047,0.034], related to intermediate plating-delayed plating. In other words, RT schedule and patient personalized treatment for lung tumors should consider intrinsic radiosensitivity both for tumoral and normal tissues, when treatment planning optimization is calculated (NTCP, normal tissues complications probability and TCP, Tumor Control Probability constitute essential complementary probabilistic parameters when designing TPO).
The influence of oxygen model is a factor to be taken into account when using BED model. The main reason is the oxygenation factor on the numerical magnitude of alpha and betha parameters. A basic model is as follows, where, ( αo , βo ) and ( αh , βh ) are the radio sensitivities under oxygenated and hypoxic conditions respectively (Malinen et al. 2006) :
αh =αo /OER and βh =βo /OER2
where,
OER : oxygen enhancement ratio.
αo : Alpha magnitude in oxygenation.
αh : Alpha magnitude in hypoxygenation.
βo : Betha magnitude in oxygenation.
βh : Betha magnitude in hypoxygenation.
This distribution of hypoxia has also been used in previous modelling studies as a consequence the proportion of the total initial number of colognes. This proportion is predicted by probability theory. The influence of oxygen is linked to models of alpha and betha parameters related to the oxygen enhancement ratio (OER), whose formula is large and not set in the paper. The most important is: If OER is higher than 1, alpha-hypoxia and betha-hypoxia decrease, then the Survival Fraction Equation negative exponential because alpha-oxygenated and Betha - oxygenated increase. Therefore, in general, oxygenated cells are more radiosensitive. Therefore, to get a survival fraction in oxygenated cells requires less radiation magnitude in general. In brief, the α-hypoxia and β-hypoxia parameters for radio sensitivity depend on PO2, and this dependence can be described by the oxygen enhancement ratio (OER). In this classical oxygenation-radiosensitivity model the most important formulas are (Malinen et al. 2006).
αh =αo /OER and βh =βo /OER2
Where, (αo , βo ) and (αh , βh ) are the radio sensitivities under oxygenated and hypoxic conditions respectively.
Today, biomarkers are getting an important role in order to predict the survival time, optimal chemotherapy, and both characteristics at the same time. Table 1 shows a biomarkers classification into P-Biomarkers (Biomarkers for Prognosis), T-Biomarkers (Biomarkers for Optimal Treatment), and H-Biomarkers (Hybrid Biomarkers Group). General Biomarkers classification. Nano-Biomarkers is an open research field with potential perspectives in future. Just remark that Biomarkers are is extent, diverse and difficult as involves biochemistry, molecular biology, medicine-pharmacology, medical physiology and several other fields. Therefore, this Table is simple based on Author’s proposal classification. Hence, Biomarkers can be classified into two groups. Namely, T-Biomarkers, those specific for treatment, and P-biomarkers, those specific for prognosis.
In recent years, the TNM stage taxonomy was improved in the seventh edition of the staging guidelines to set a combination of TNM parameters with survival outcomes rates and treatment optimal choices among stages [refs]. Then, interrelated with TNM stages, mainly the survival rate, and prognosis rate, location, types of selected treatment strategies, divided into in stages I, II, III and IV are nowadays considered complementary. TNM classification has also defined survival rates for every stage. For example, T1a and IA show get the approximately equal survival rate after 5 years of about 50%. The interrelation of both criteria can be considered complex, since survival outcomes, surgery resection indication, RT treatment, chemotherapy and immunotherapy are linked to several stages of both taxonomies. For early stage : CT screening proven e useful. Low dose CT was proven be useful in screening . Screenings to get an early-stage diagnosis, and obtain an optimal treatment, are focused mainly on selected population smokers and high-risk professions risk factors (such as toxic chemicals). TNM classification complemented with histologic grade is used today for precise diagnosis-stage of lung tumors. For example, TIa stage shows be the best survival rate after 5 years, 70%, while IV has a 10% .Pleural invasion, particularly the presence of tumor at the surface of the visceral pleura, has been an indicator of a poor prognosis.
Since radiotherapy treatment is indicated in all TNM lung cancer stages, it is possible to set a practical classification for specific lung tumor RT treatment, [author’s proposal] . PTV Type 1 is a clinical planning for T and N stages located within thorax or very close into thorax to lungs. PTV Type 2 is the RT planning for N and M stages which are not close to primary lung tumor, such as, upper nodules at cervical-neck level, distant axile nodules or brain metastases. Radiation therapy treatment is applied at all stages of lung cancer. Even at M stage, the brain metastases are treated with radiation, and when their diameter are about 5cm, radiosurgery is indicated. Lung radiation has special anatomical and physiological constraints compared to other organs. Some of them are lung density inhomogeneity, which is a synergic difficulty with PTV volume changes with lung breath dynamics. During radiation delivery, the lung tumor target borders could vary about 2-3cm, and at the same time that implied a dynamic density PTV change.
Radiotherapy biological models come from initial radiobiological theoretical and experimental studies [75,87-88,91]. Radiobiological interaction with normal tissues was researched for radioprotection [76-80]. Then, two practical branches emerged simultaneously from the equivalent mathematical modelling investigation. Namely, to use radiobiology knowledge for radiation protection of normal tissues, and conversely to set radiobiological models to approach/improve the cell-kill method in tumoral tissues [22-25,89-91]. From this branch-duality, a practical swapping of equivalent parameters emerged for practical/easier research and clinical-biological applications. For instance [α,β] typical Linear Quadratic models parameters. These mathematical models both for normal and tumoral tissues were usually based on exponentials whose power-functions depend on a linear/nonlinear equation of radiation dose variable with a number of experimentally validated coefficients/constants [22-25,76-80,87- 91,92-96].
The previous works and novelty in this artificial intelligence method for hyperfractionation precision-schedule method, [91,98,99,105], showed accurate results for survival fractions, 3D Graphical Optimization charts, and a database of numerical results in other type of cancer, e. g. , prostate. To reach the research objectives in this study, nonlinear GA-PMO engineering software was programs for PMO-BED Lung cancer basic model. The implemented specific software got to get going towards improvements in GA programming and TPO radiotherapy optimization for BED model hyperfractionated dose delivery protocol [91].
Therefore, the innovation of this contribution shows a number of aspects. The first one is the application of Pareto-Multi objective Optimization methods for lung cancer with in vivo dataset. The second one is the 3D Isodose lines in TPO with new imaging results, based on previous recognized publications [91,98,99,105]. The third is also the presentation of 3D Isodose zones improved imaging-processing results based on another recent article. Previous work with these methods belong to prostate tumors and lung ones [91,98,99,105]. The primary algorithms and software results for these Pareto-Multi objective Optimization were initially developed in these contributions.
Consequently, the innovation of this study is to carry out AI-GA programming for lung cancer hyperfractionation TPO in BED models. Several simulations with Genetic Algorithms are shown in 2D charts and numerical results. The algorithm for multi objective pareto optimization is detailed and programmed. Results comprise GA simulations for two types of parameters-BED models according to literature [75,87,88,91]. MATLAB system was used for GA programming with acceptable graphical processing images and numerical data findings. Succinctly, advanced research from former Nonlinear Pareto-Multi objective GA optimization was got for BED models in Lung cancer [87,88,91]. Applications for radiotherapy TPO, dose delivery hyperfractionation schedule future biological model advances in modern RT are also presented.
Mathematical Algorithms and Software Engineering Methods
The model set in software patterns is the basic BED one [20-25,89]. There is a number of variations/simplifications of this model in the literature [20-25,39,40,75,85,91]. One reason is that the radiobiological parameters determination vary according to experimental radiobiology data findings [20-25]. Therefore, those simplified BED models take statistical values of, for example, Potential and others. In this section the algorithm is explained, at Results one, the Pareto-Multi objective Optimization method parameters to put forward sharply the graphs are detailed. Besides, in biological models TPO applications, there is a medical physics controversy/discussion about Hyperfractionation versus Hypofractionation dose TPO delivery. That point is beyond the scope of this study since the objective of the research is AI-GA optimization of hyperfractionation dose. In this section the algorithms are explained, and at results one, the Pareto-Multi objective Optimization method parameters to put forward sharply the graphs are detailed. However, for sharp learning, Table 2 shows the main simplified concepts of Genetic Algorithms applied on Pareto-Multi objective Optimization.
It is very frequent the application of inverse least square techniques for RT inverse planning. Genetic algorithms constitute a more modern method, and GA Pareto-Multi objective has also been applied recently [58,67]. The genetic algorithms (GA) optimization method, closely linked to modern artificial intelligence, has experienced a recent increase in the use of its optimization applications/variants [ 58,67]. Although the applied GA method in this contribution is the standard, each one of the GA variants has its advantages and disadvantages [10,11]. Basically, GA is a stochastic mixed method similar to Monte Carlo but simpler/faster in general. That is, in plain language, successive generations of values (parameters) are computed by the software until the optimal parameters figures are obtained. Actually, the multiple combinations of random/stochastic methods, GA variants, and modern programming techniques, offer an extensive choice of options for the optimization designer. In this article, the parameters, namely, are, dose fraction magnitude, number of fractions, and total treatment time.
Therefore, here GA usually selects a randomly large number of successive generations of dose fractions number, fraction magnitude, and total treatment time, for the objective function maxima accuracy subject to constraints-desired intervals for dose fractions number, fraction magnitude, and total treatment time. For every generation, three types of choices are applied for the OF. Namely, elite selection, after-mutations, and cross-over changes in the variables’ values. GA program stops when the number of generations subject to the constrains and/or the numerical tolerance for a generation is reached even if that solution is a local or global minimum. In other words, speaking roughly, GA stops when the best-possible and desired data for TPO that is needed is obtained.
Pareto-Multi objective method is a specific optimization one, and here is implemented with GA. This method, for example, is extensively used also in economics to obtain optimal-comparative values for two options (actually 3 ones is possible). Namely, Objective 1 and Objective 2. The method of multi objective optimization for simple constraints begin with setting an objective function for the two different objectives with this type of functions:
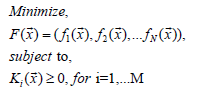
Where,
F(x) : Main function to be optimized.
fi( x ) : Every function of same variables ( x ).
Ki(x) : Constraints functions such as in general N ≠ M .
Algorithm 1- The basic concepts of constrained Multi objective Optimization. Then, two alternatives (in paper total dose 50-55 Gy for Pareto1, and 60-65 for Pareto2, and for second simulation, 60 Gy Pareto1 and 65 Gy Pareto2, see all Table 1 & 2) are set within a built OF.

First we get the bed model as it was done for head and neck cancer in previous publications

Second Step: Setting This Model In L1 Objective Function: Therefore, the Pareto-Multi objective Optimization basic BED Effective created in this contribution algorithm-model was set in software, [91]. Parameters are detailed in Algorithm 1 [85-91]. Two different PMO optimization programming series are presented with different parameter intervals magnitudes, Table 1 & 2. This BED model constitutes the fundamentals for fractionate radiotherapy, although there are variations among authors [22-25]. Formulation is based on previous studies computational software [1-21,85-91]. The algorithm that was set, with Chebyshev L1 norm, [Algorithm 1], reads,

Where,
BED : The basic algorithm for Biological Effective Dose initially developed [22-25,89].
K : Optimal Number of fractions for hyperfractionated TPO. Optimization parameter [22-25,89].
D : Optimal Dose magnitude for every fraction. Optimization Parameter [ Gy ]. [22-25,89].
A : The basic algorithm constant for Biological Effective Dose models. Radiobiological experimental parameter. [ Gy-1 ]. [22-25,89].
Β : The basic algorithm constant for Biological Effective Dose models. Radiobiological experimental parameter . [ Gy-2 ]. It is very usual to set in biological models [ α / β in Gy].
TTreatment : The overall TPO time. This parameter varies according to authors’ and institutions/hospitals criteria. [22-25,89].
TDelay : The overall TPO time delay for colognes re-activation. This parameter varies according to authors’ experimental research.
Totential : The potential time delay for tumor cell duplication. This parameter varies according to authors’ experimental-theoretical research.
DOSE : The dose magnitudes for lung cancer simulation algorithm for Biological Effective Dose [22-25,89]. Software patterns were calculated around intervals lung DOSE ϵ [50,65] Gy.
Algorithm 2- Lung cancer PMO algorithm [1-21,85-88] set in software loops, patterns, and arrays for AI-GA. The parameters interval-magnitudes for optimization are detailed in Table 1 & 2. It is an improvement from a series of previous research in radiotherapy PMO-AI for Breast and Head and Neck tumors [75,87-88,91].
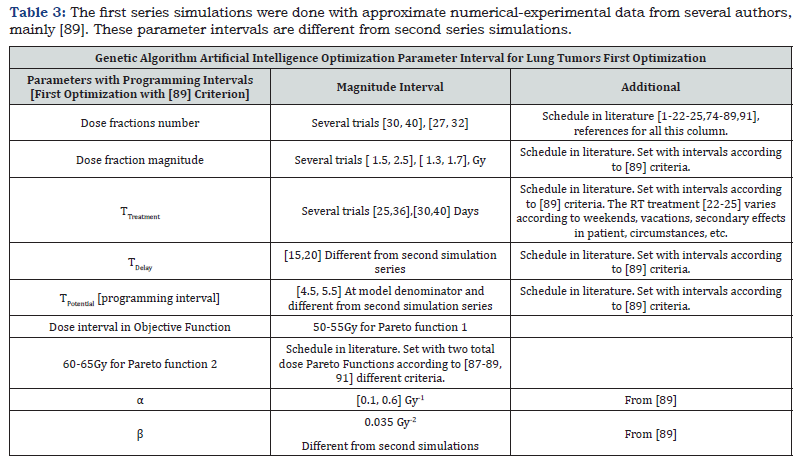
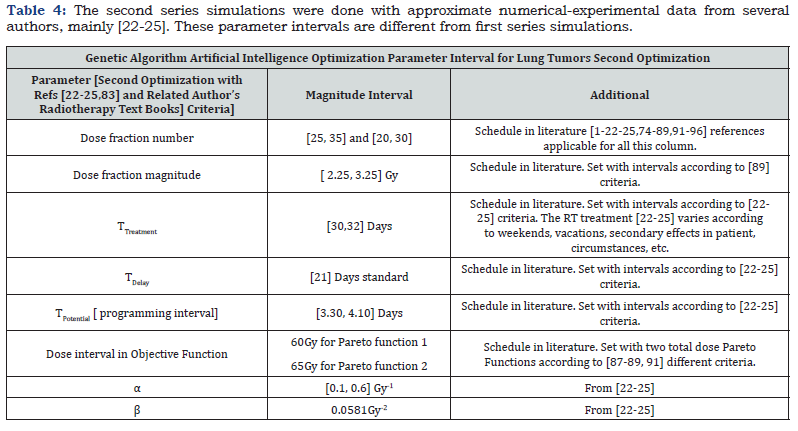
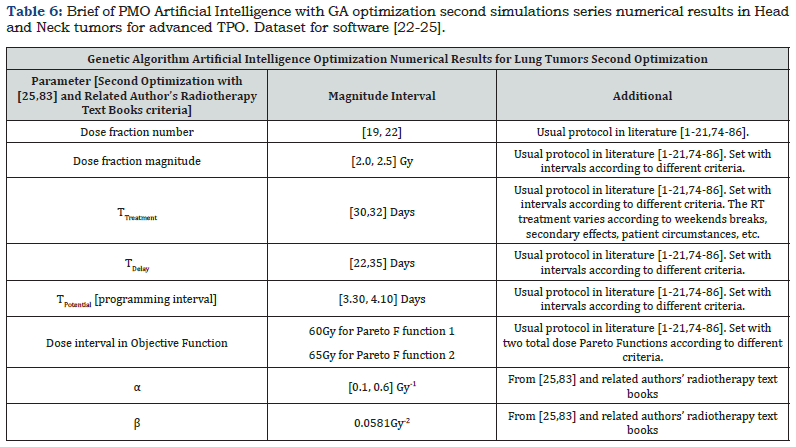
Pareto-Multi objective Dataset For Lung Cancer Optimization: In the following, Table 2 shows the first simulation series according to data from [89]. Table 3 & 4 details dataset for second simulations series with experimental-theoretical magnitudes from [22-25]. In programming task, several trials around these values were done.
Results
Results
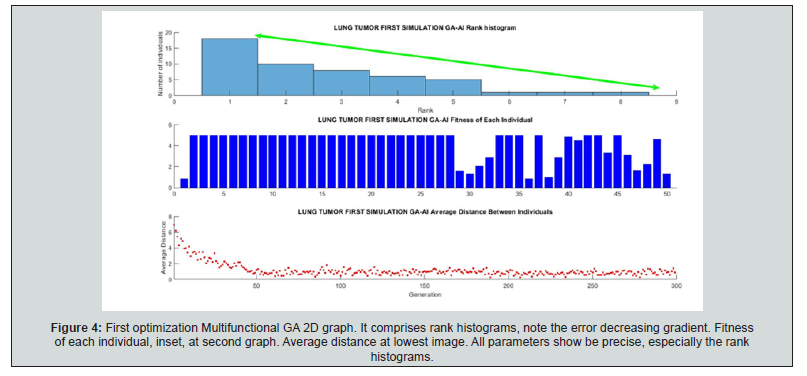
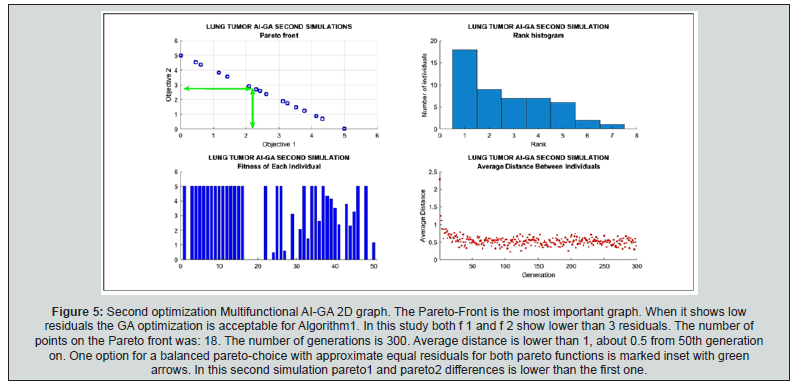
Results are 2D AI-GA graphical and numerical. As shown in Table 2, the most important GA parameters are presented and explained. That is, Best Fit, Number of Generations and Pareto-Front. In Pareto-Front, the optimal point was selected to get the best results, Figure 1-5. Figure 6 & 7 show the histograms score data results, that is, the difference between the pareto1 and pareto2 scores. For first simulations, Figure 1-4 show PMO results-Figure 3.1 is a variant of Figure 3. For the second group, 2D imaging processing are Figure 5-7. Table 3 & 4 present details of both numerical PMO optimization results. The most important to validate the results are those ones that show the Pareto Front. Average distance among generation individuals, score histograms, stopping criteria, or fitness for every individual, are also significant. All the complementary details and shown in additional 2D charts for first and second AI-GA PMO optimization. Maximum number of generations programmed is 300. Some other generations number to compare were selected as 100, General running time range for all images and both optimization trials is about 2-6 minutes. Numerical results, Table 3 & 4, resume for PMO in BED model. Dose fraction magnitudes, number of fractions and optimal total RT treatment values are explained in Table 3 & 4.
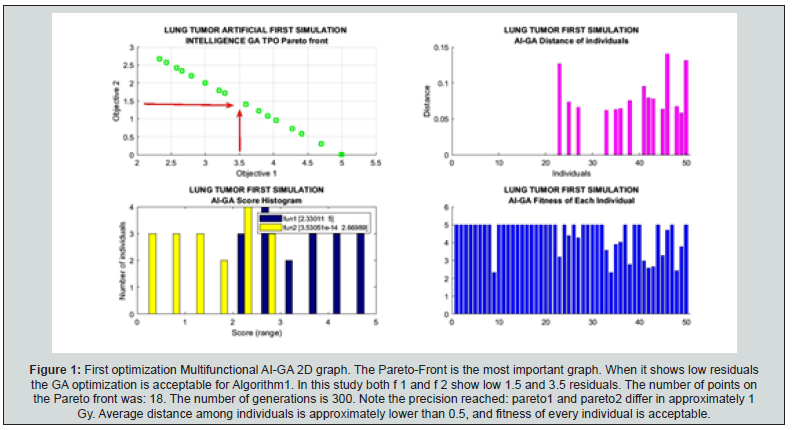
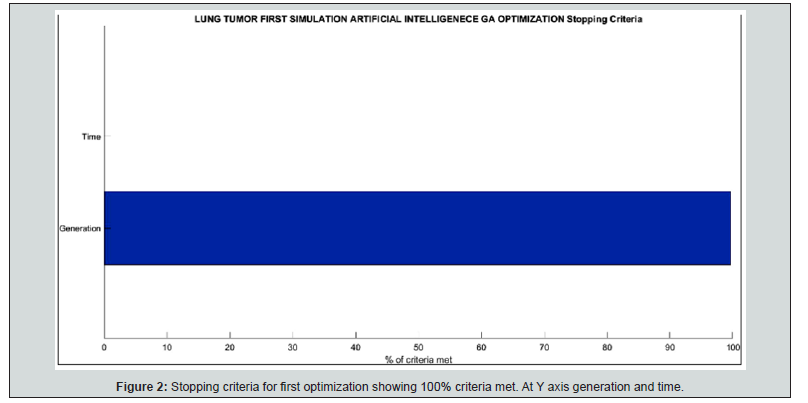
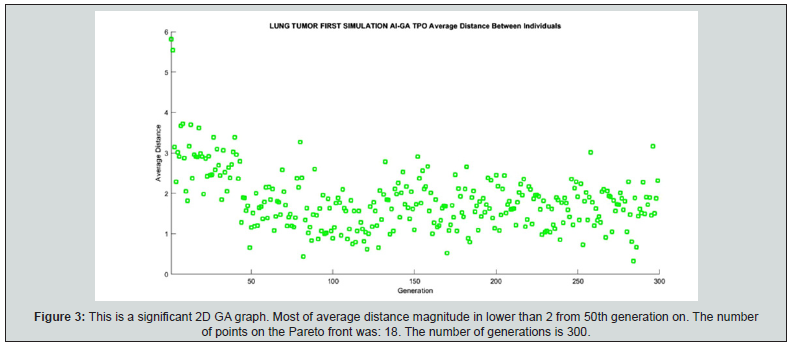
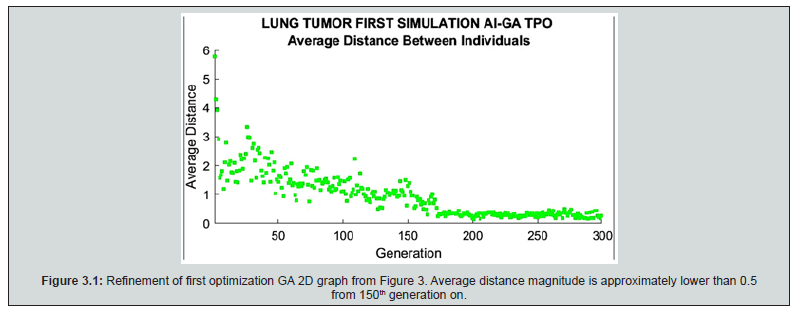


GA 2D results
First simulation 2D GA results are shown in Figure 1-4. The data for first and second simulation is set at Table 3 & 4. Second one is presented in Figure 5-8. There are simple image processing charts and multifunctional images also. In Figure 1, the most important is the Pareto-Front first chart. Complementary, the Distance among individuals and the fitness of each individual is shown, concepts in Table 2.
GA Numerical results
This section shows a brief of numerical dataset corresponding to imaging processing AI-GA results, Table 4 & 5. It is useful to compare the dose per fraction and number of fractions among all optimal results.
First simulation numerical results
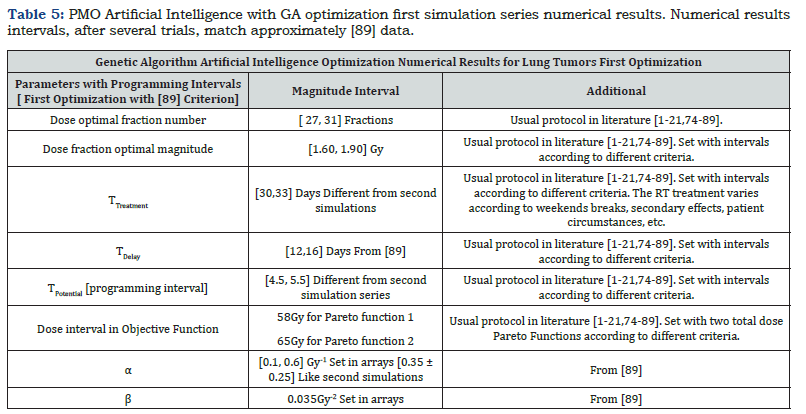
The first simulation results are shown in Table 5. The second in Table 6. Main comparison should be among dose per fraction and number of fractions. Results are according to literature and recent advances several hospital data.
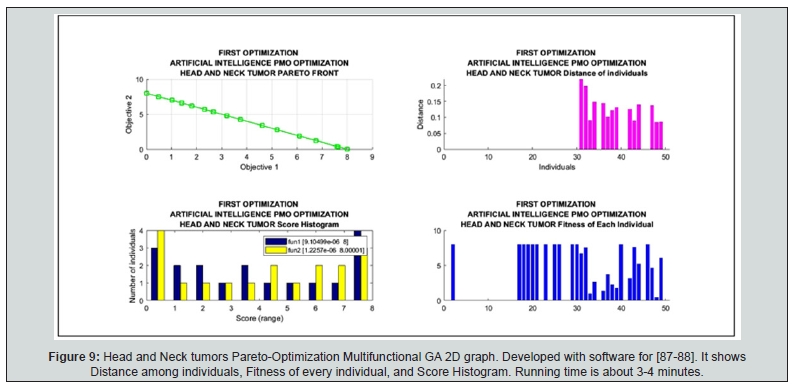
Comparative results with head and neck cancer ai-ga optimization research
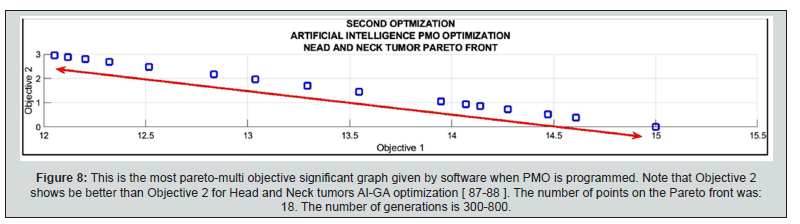
AI-GA comparison with the same method for Head and Neck tumors, Figure 8 & 9. These images included here are newly-developed different imaging processing PMO results than obtained in [87]. The most significant to check the results are the Pareto Front images, Figure 8. Figure 9 is a multifunctional image AI-GA processing for Head and Neck cancer RT treatment based on [87,91] software. Distance among individuals, score histograms, and fitness of every individual are shown, Figure 9. Maximum number of generations selected was 300-800. Running time for Figure 8 is shorten than Figure 9, both processes is from 2 to 6 minutes.
Discussion and Conclusion
The objectives of the study were graphical and numerical optimization of standard BED model for modern Lung cancer TPO. The method applied was Artificial intelligence with GA Pareto-Multi objective Optimization. It is the same technique from previous research with BED model for Breast and Head and Neck tumors TPO. Optimization was performed according to two authors’ biological BED models criteria [22-25, 87-89,91]. Therefore, it constitutes a step forward to apply GA for Lung cancer TPO advances. The mathematical method applied is Pareto-Multi objective Optimization. The advantage of 2D Multi objective Optimization compared to common one is to obtain at least two pareto functions, and the optimal choice can be got selecting the most convenient data from objective 1 and objective 2 graphs (Figure 1,8,9). Compared to Tikhonov Inverse Optimization method, that was applied in previous publications, that constitutes an advantage [21,75]. However, classical Tikhonov methods can be considered precise and useful. A useful-comprehensive simplification of the GA-PMO method was shown in Table 2. Complementary, and specifically for lung tumors, a Biomarkers Author’s proposal of modern classification based on [101,108,109].
The BED model algorithm that was selected is the standard one of the first generation. For hyperfractionation as a first step research choice [25,83]. The numerical difference has not been checked implementing further generations of BED algorithms. However, as a tentative calculus given the numerical data obtained, it seems that the numerical differences could not differ significantly from the first-generation model function. The L1 norm selected (Tikhonov L1 norm) was applied for programming simplification. In previous articles, it was found that software implementation of (Tikhonov L2) norm did not show substantial differences with L1 norm. Besides, the design of the program for L2 norm results be more complicated and does not bring important variances. Other features that the implementation of the L2 norm implies a longer running time, which is an added difficulty. First simulation shows higher number of fractions, and lower magnitude of dose per fraction than the second simulation, Table 5 & 6.
Factually, and according to recent literature [101-109], GA-PMO method is more widely used compared to Inverse Optimization with Least Squares algorithm, for example, [11-16]. Recent optimization methods tend to apply/use more frequently evolutionary algorithms and also the variants and improved GA algorithms based on successive method-generations. 3D-imaging Interior Optimization (the basic) was implemented, e.g., for superconductors modelling with acceptable numerical results in a series of publications, for example. Although 3D-IO technique is essentially a numerical imaging-processing one, the 2D GA-PMO method gives also acceptable information and dataset for the approached problem.
The software that was designed for the research is based on previous studies for applications of GA standard method . The implemented dataset is founded on the lung cancer current protocol doses and do not differ in magnitude order along the literature. As an example, these calculations boundaries and magnitude orders were modernly confirmed . Therefore, the constraints and boundaries set in programming patterns can be considered acceptable. In terms of programming running time, it was checked that the approximate average time to obtain a simple GA chart was about 2 minutes, provided that number of generations not be higher than (200, 300). If the generations number increases from 150, approximately, the running time could reach 3 or 4 minutes. The Multi graphics take an average of 2 minutes more than the simple ones.
The numerical data obtained matches the average literature dataset [99], with very low differences. Specially the recent protocols in Radiosurgery [100], coincide with the dosimetry results. When number of generations is increased, no significant changes are observed in magnitude orders for Pareto 1 and 2 Multi objective Functions. The objective of the study was not discussed between hyperfractionation versus hypofractionation. However, according to results it is possible to comment some classical ideas about this controversial matter. There are Hyperfractionation, Hypofractionation, Hybrid Schedule and Accelerated Hyperfractionation dose delivery schedules. Hospital institutions differ in technical facilities, staff specialization, and treatment time avail-able, therefore this question adds another influential factor for those optimal clinical-radiation oncology decisions.
Author’s criterion is that all of them should be treated/considered in function of personalized RT treatment, and the most important idea is that all of them depend on multiple factors [22-25,87-89,91]. one im-portent factor is the magnitude order of the coefficients alpha and betha for tumoral tissue at every patient, if time and hospital facilities can determine those. Hyperfractionation considers that the higher recovery capacity of late-responding normal tissues, in practical terms NTCP magnitude, is higher when contrasted with tumor-tissue. If the response of normal tissues is low, it implies that the quotient ( alpha/betha ) has a lower magnitude order) . However, the more fractions get the schedule, the higher changes of this quotient is observed. For comparative considerations between Hyper and Hypofractionation. The dose difference between the plotting’s of TCP versus dose fraction magnitude gives essential information for selecting options in dose delivery schedule.
The PMO-BED model image processing results are sharp in several imaging formats, from simple 2D graphics to multifunctional ones. These series of results can be considered acceptable, Figure 1-9, Table 3 & 4. Two simulations were presented as objective of the research, computationally designed for head and neck tumors [82-88]. It was intended to set in software precise experimental constants [22,81-88]. Therefore, 3D simulations could offer a realistic graphical and numerical dataset this type of cancers. Two different simulations with different constraints are shown and proven. Currently, biological models get a rationale experimental proven through radiobiology studies [76-80]. TCP and NTCP constitute acceptable parameters to predict patient survival time [20,87-88]. The method main advantages are graphics sharpness, low numerical residuals, demonstration of operability of this modern AI method, and contrast between two different BED criteria parameters. Inconvenient are that in literature experimental data parameters differ numerically [87-88,91]. The algorithm is based on the simplest BED model [22-25] at this stage. Running time is rather longer compared to Inverse Least Squares Optimization [1-21]. Grosso modo, Pareto Multi objective BED model was got for applied for optimization of radiotherapy BED algorithm in Lung cancer. The practical radiotherapy physics significance is an improved radiation therapy treatment for these tumors RT medical physics computational planning.
Scientific Ethics Standards
This article shows additional results that complement previous studies and contributions, recently [87-88]. All the images are new/improved and numerical results from former publications are extended and detailed. GA Artificial Intelligence software was developed originally by Dr Casesnoves on September 2022. Figure 8 & 9 are new but developed from software in [87,88,91]. All initial modelling equations were developed from previous researchers contributions [1-25,87-88]. This article has previous papers mathematical techniques, reviews with explanations, [1-21,75], whose use was essential to make model numerical solutions and approximations. The number of Dr Casesnoves publications at references is intended also for reader’s learning and consultation. This study was carried out, and their contents are done according to the European Union Technology and Science Ethics and International Scientific Ethics norms [38,43-45].
This research was completely done by the author, the calculations, images, mathematical propositions and statements, reference citations, and text is original from the author. When a mathematical statement, proposition or theorem is presented, demonstration is always included. If any results inconsistency is found after publication, it is clarified in subsequent contributions. When a citation such as [Casesnoves, ‘year’] appears, there is not vanity or intention to brag. The reason is to keep clearly the intellectual property. The article is exclusively scientific, without any commercial, institutional, academic, religious, religious-similar, non-scientific theories, personal opinions, friends and/or relatives favors, political ideas, or economical influences. When anything is taken from a source, it is adequately recognized. Ideas and some text expressions/sentences from previous publications were emphasized due to a clarification aim [38,43-45].
References
- Casesnoves F (2022) Radiotherapy Wedge Filter AAA Model 18 MeV Dose Delivery 3D Simulations with Several Software Systems for Medical Physics Applications. Applications. Biomed J Sci & Tech Res 40(5).
- Casesnoves F (2016) Mathematical Exact 3D Integral Equation Determination for Radiotherapy Wedge Filter Convolution Factor with Algorithms and Numerical Simulations. Journal of Numerical Analysis and Applied Mathematics 1(2): 39-59.
- Casesnoves F (2015) Radiotherapy Conformal Wedge Computational Simulations, Optimization Algorithms, and Exact Limit Angle Approach. International Journal of Scientific Research in Science, Engineering and Technology (IJSRSET) 1(2): 353-362.
- Casesnoves F (2019) Improvements in Simulations for Radiotherapy Wedge Filter dose and AAA-Convolution Factor Algorithms. International Journal of Scientific Research in Science, Engineering and Technology (IJSRSET) 6(4): 194-219.
- Casesnoves F (2011) Exact/Approximated Geometrical Determinations of IMRT Photon Pencil-Beam Path Through Alloy Static Wedges in Radiotherapy Using Anisothropic Analytic Algorithm (AAA). Peer-reviewed ASME Conference Paper. ASME 2011 International Mechanical Eng Congress. Denver. USA.
- Casesnoves F (2012) Geometrical Determinations of Limit angle (LA) related to maximum Pencil-Beam Divergence Angle in Radiotherapy Wedges. Peer-reviewed ASME Conference Paper. ASME 2012 International Mechanical Eng Congress. Houston. USA.
- Casesnoves F (2013) A Conformal Radiotherapy Wedge Filter Design. Computational and Mathematical Model/Simulation’. Peer-Reviewed Poster IEEE (Institute for Electrical and Electronics Engineers), Northeast Bioengineering Conference. Syracuse New York, USA.
- Casesnoves F (2014) Mathematical and Geometrical Formulation/Analysis for Beam Limit Divergence Angle in Radiotherapy Wedges. Peer-Reviewed International Engineering Article. International Journal of Engineering and Innovative Technology (IJEIT) 3(7).
- Casesnoves F (2014) Geometrical determinations of IMRT photon pencil-beam path in radiotherapy wedges and limit divergence angle with the Anisotropic Analytic Algorithm (AAA) Casesnoves, F. Peer- Reviewed scientific paper, both Print and online. International Journal of Cancer Therapy and Oncology 2(3): 02031.
- Casesnoves F (2014) Radiotherapy Conformal Wedge Computational Simulations and Nonlinear Optimization Algorithms. Peer-reviewed Article, Special Double-Blind Peer-reviewed paper by International Scientific Board with contributed talk. Official Proceedings of Bio- and Medical Informatics and Cybernetics: BMIC 2014 in the context of the 18th Multi-conference on Systemics, Cybernetics and Informatics: WMSCI 2014 July 15 - 18, 2014, Orlando, Florida, USA.
- Casesnoves F (2007) Large-Scale Matlab Optimization Toolbox (MOT) Computing Methods in Radiotherapy Inverse Treatment Planning’. High Performance Computing Meeting. Nottingham University. Conference Poster.
- Casesnoves F (2008) A Computational Radiotherapy Optimization Method for Inverse Planning with Static Wedges. High Performance Computing Conference. Nottingham University. Conference Poster.
- Casesnoves F (2015) Radiotherapy Standard/Conformal Wedge IMRT-Beamlet Divergence Angle Limit Exact Method, Mathematical Formulation, and Bioengineering Applications. International Article-Poster. Published in Proceedings of Conference. 41st Annual Northeast Bioengineering Conference. Rensselaer Polytechnic Institute. Troy, New York USA p. 17-19.
- Casesnoves F (2015) Radiotherapy Standard/Conformal Wedge IMRT-Beamlet Divergence Angle Limit Exact Method, Mathematical Formulation, and Bioengineering Applications. IEEE (Institute for Electrical and Electronics Engineers), International Article-Poster.
- Casesnoves F (2015) Abstract-Journal. Radiotherapy Standard/ Conformal Wedge IMRT-Beamlet Divergence Angle Limit Exact Method, Mathematical Formulation. International Conference on Significant Advances in Biomedical Engineering. 2nd OMICS International Conference 5(1).
- Casesnoves F (2001) Determination of absorbed doses in common radio diagnostic explorations. 5th National Meeting of Medical Physics. Madrid, Spain. September 1985. treatment Planning.
- Casesnoves F (2001) Master Thesis in Medical Physics. Eastern Finland University. Radiotherapy Department of Kuopio University Hospital and Radiotherapy Physics University-Kuopio. Defense approved in 2001. Library of Eastern Finland University. Finland.
- Casesnoves F (2013) A Conformal Radiotherapy Wedge Filter Design. Computational and Mathematical Model/Simulation’. Peer-Reviewed Poster IEEE (Institute for Electrical and Electronics Engineers), Northeast Bioengineering Conference. Syracuse New York, USA.
- Casesnoves F (2022) Radiotherapy Biological Tumor Control Probability Integral Equation Model with Analytic Determination. International Journal of Mathematics and Computer Research 10(8): 2840-2846.
- Casesnoves F (2022) Radiotherapy Wedge Filter AAA Model 3D Simulations For 18 Mev 5 cm-Depth Dose with Medical Physics Applications, International Journal of Scientific Research in Computer Science, Engineering and Information Technology (IJSRCSEIT) 8(1): 261-274.
- Walsh S (2011) Radiobiological modelling in Radiation Oncology. PhD Thesis. School of Physics. National University of Galway.
- Chapman D, Nahum, A (2015) Radiotherapy Treatment Planning, Linear- Quadratic Radiobiology. CRC Press.
- Mayles W, Nahum A (2015) In: Rosenwald J (Ed.), Handbook of Radiotherapy Physics. Second Edition. CRC Press.
- Nahum A, Webb S (1993) A model for calculating tumor control probability in radiotherapy including the effects of inhomogeneous distributions of dose and clonogenic cell density. Phys Med Biol 38(6): 653-666 .
- Haydaroglu A, Ozyigit G (2013) Principles and Practice of Modern Radiotherapy Techniques in Breast Cancer.
- Casesnoves F (2019-20) The Numerical Reuleaux Method: Computational and Dynamic Fundamentals with Applications (Part One).
- Ulmer W, Harder D (1997) Corrected Tables of the Area Integral I(z) for the Triple Gaussian Pencil Beam Model. Z Med Phys 7: 192-193.
- Ulmer W, Harder D (1995) A triple Gaussian pencil beam model for photon beam treatment planning. Med Phys 5: 25-30.
- Ulmer W, Harder D (1996) Applications of a triple Gaussian pencil beam model for photon beam treatment planning. Med Phys 6: 68-74.
- Ma C, Lomax T (2013) Proton and Carbon Ion Therapy. CRC Press.
- Censor Y, Zenios S (1997) Parallel Optimization: Theory, Algorithms and Applications’. UOP.
- Ulmer W, Pyyry J, Kaissl W (2005) A 3D photon superposition/ convolution algorithm and its foundation on results of Monte Carlo calculations. Phys Med Biol, p. 50.
- Ulmer W, Harder D (1997) Applications of the triple Gaussian Photon Pencil Beam Model to irregular Fields, dynamical Collimators and circular Fields. Phys Med Biol.
- Haddad K, Anjak O, Yousef B (2019) Neutron and high energy photon fluence estimation in CLINAC using gold activation foils. Reports of Practical Oncology and Radiotherapy 24: 41-46.
- Sievinen J, Waldemar U, Kaissl W. AAA Photon Dose Calculation Model in Eclipse™. Varian Medical Systems Report. Rad #7170A.
- Vagena E, Stoulos S, Manolopoulou M (2016) GEANT4 Simulations on Medical LINAC operation at 18MV: experimental validation based on activation foils. Radiation Physics and Chemistry.
- Ethics for Researchers (2013) EU Commission. Directorate-General for Research and Innovation. Science in society/Capacities FP7.
- Casesnoves F (1981) Surgical Pathology I course class notes and clinical practice of Surgical Pathology Madrid Clinical Hospital [ Professor Surgeon Dr Santiago Tamames Escobar ]. 4th academic year course for graduation in Medicine and Surgery. Lessons and practice Lung Cancer Surgical and Medical Treatment. 1980-1981. Madrid Complutense University.
- Tamames Escobar S (2000) Cirugia/ Surgery: Aparato Digestivo. Aparato Circulatorio. Aparato Respiratorio/ Digestive System. Circulatory System. Respiratory System (Spanish Edition).
- Silvia CF, Sandra D (2013) Combining Radiotherapy and Cancer Immunotherapy: A Paradigm Shift Silvia C. Formenti, Sandra Demaria. J Natl Cancer Inst 105: 256-265.
- Numrich R (2010) The computational energy spectrum of a program as it executes. Journal of Supercomputing.
- European Commission, Directorate-General for Research (2021) Unit L3. Governance and Ethics. European Research Area. Science and Society.
- ALLEA (2017) The European Code of Conduct for Research Integrity, Revised Edn.; ALLEA: Berlin Barndenburg Academy of Sciences.
- Good Research Practice (2017) Swedish Research Council.
- Ulmer W, Schaffner B (2011) Foundation of an analytical proton beamlet model for inclusion in a general proton dose calculation system. Radiation Physics and Chemistry 80: 378-389.
- Sharma S (2008) Beam Modification Devices in Radiotherapy. Lecture at Radiotherapy Department, PGIMER. India.
- Barrett A, Colls (2009) Practical Radiotherapy Planning. Fourth Edition. Hodder Arnold.
- Ahnesjö A, Saxner M, A Trepp (1992) A pencil beam model for photon dose calculations. Med Phys, pp. 263- 273.
- Brahime A (2000) Development of Radiation Therapy Optimization. Acta Oncologica 39(5).
- Bortfeld T, Hong T, Craft D, Carlsson F (2008) Multicriteria Optimization in Intensity-Modulated Radiation Therapy Treatment Planning for Locally Advanced Cancer of the Pancreatic Head. International Journal of Radiation Oncology and Biology Physics 72(4).
- Brown, B (2014) Clinician-led improvement in cancer care (CLICC) - testing a multifaceted implementation strategy to increase evidence-based prostate cancer care: phased randomised controlled trial - study protocol. Implement Sci 9: 64.
- Bortifield T (2006) IMRT: a review and preview. Phys Med Biol 51(2006): R363–R379.
- Censor Y (1996) Mathematical Optimization for the Inverse problem of Intensity-Modulated Radiation Therapy. Laboratory Report, Department of Mathematics, University of Haifa, Israel.
- Capizzello A, Tsekeris PG, Pakos EE, Papathanasopoulou V, Pitouli EJ (2006) Adjuvant Chemo-Radiotherapy in Patients with Gastric Cancer. Indian Journal of Cancer 43(4).
- Tamer D, Abdelrazek EM, Mostafa E, Rehab O (2014) Dose Validation of Physical Wedged symmetric Fields in Artiste Linear Accelerator. International Journal of Medical Physics, Clinical Engineering and Radiation Oncology 3: 201-209.
- Do SY, David A, Bush JDS (2010) Comorbidity-Adjusted Survival in Early-Stage Lung Cancer Patients Treated with Hypofractioned Proton Therapy. Journal of Oncology.
- Ehrgott M, Burjony M (1999) Radiation Therapy Planning by Multicriteria Optimization. Department of Engineering Science. University of Auckland. New Zealand. Conference Paper.
- Ezzel G (1996) Genetic and geometric optimization of three-dimensional radiation therapy treatment planning. Med Phys 23: 293- 305.
- Effective Health Care (2008) Comparative Effectiveness of Therapies for Clinically Localized Prostate cancer. Bookshelf ID: NBK554842 .
- Hansen P (1998) Rank-deficient and discrete ill-posed problems: numerical aspects of linear inversion’. SIAM monographs on mathematical modelling and computation.
- Hashemiparast, S, Fallahgoul H (2011) Modified Gauss quadrature for ill-posed integral transform. International Journal of Mathematics and Computation 13(11).
- Isa N (2014) Evidence based radiation oncology with existing technology. Reports of Practical Oncology and Radiotherapy 19: 259-266.
- Johansson KA, Mattsson S, Brahme A, Turesson I (2003) Radiation Therapy Dose Delivery. Acta Oncologica 42(2): 2003.
- Khanna P, Blais N, Gaudreau PO, Corrales-Rodriguez L (2016) Immunotherapy Comes of Age in Lung Cancer, Clinical Lung Cancer.
- Kufer KH, Hamacher HW, Bortfeld T (2000) A multicriteria optimization approach for inverse radiotherapy planning. University of Kaiserslautern, Germany.
- Kirsch A (1996) An introduction to the Mathematical Theory of Inverse Problems. Springer Applied Mathematical Sciences.
- Luenberger D (1989) Linear and Nonlinear Programming (2nd). Addison-Wesley.
- Moczko J, Roszak A (2006) Application of Mathematical Modeling in Survival Time Prediction for Females with Advanced Cervical cancer treated Radio-chemotherapy. Computational Methods in Science and Technology 12(2).
- Ragaz J, Ivo AO, John JS, Norman P, Stewart MJ (2005) Regional Radiation Therapy in Patients with High-risk Breast Cancer Receiving Adjuvant Chemotherapy: 20-Year Results of the Columbia Randomized Trial’. Journal of National Cancer Institute 97(2).
- Steuer R (1986) Multiple Criteria Optimization: Theory, Computation and Application. Wiley.
- Spirou SV, Chui CS (1998) A gradient inverse planning algorithm with dose-volume constraints. Med Phys 25: 321-323.
- Das I, Colls (1997) Patterns of dose variability in radiation prescription of breast cancer. Radiotherapy and Oncology 44: 83-89.
- Casesnoves F (2018) Practical Radiotherapy TPO course and practice with Cyberknife. Robotic simulations for breathing movements during radiotherapy treatment. Sigulda Radiotherapy Cyberknife Center. Latvia. Riga National Health Oncology Hospital Varian LINACs TPO practice/lessons several Varian LINACs. Riga Technical University Bioengineering Training-Course Nonlinear Life.
- Casesnoves F (2022) Radiotherapy Linear Quadratic Bio Model 3D Wedge Filter Dose Simulations for AAA Photon-Model [18 Mev, Z= 5,15 cm] with Mathematical Method System. Biomed J Sci & Tech Res 46(2).
- Casesnoves F (1985) Master in Philosophy Thesis at Medical Physics Department. Protection of the Patient in Routinary Radiological Explorations. Experimental Low Energies RX Dosimetry. Medicine Faculty. Madrid Complutense University.
- Casesnoves F (1983-5) Ionization Chamber Low Energies Experimental Measurements for M-640 General Electric RX Tube with Radcheck ionization camera, Radcheck Beam Kilovoltimeter and TLD dosimeters. Radiology Department practice and measurements. Madrid Central Defense Hospital. Medical Physics Department. Master in Philosophy Thesis. Medicine Faculty. Complutense University. Madrid.
- Casesnoves F (1985) Determination of Absorbed Doses in Routinary Radiological Explorations. Medical Physics Conference organized by Medical Physics Society Proceedings Printed. San Lorenzo del Escorial. Madrid.
- Greening J (1985) Fundamentals of Radiation Dosimetry. Taylor and Francis. Second Edition.
- International Commission of Radiation Protection (1977) Bulletin 26th. The International Commission on Radiological Protection. Recommendations of the International Commission on Radiological Protection. Pergamon Press.
- Stanton P (1996) Cell kinetics in vivo of human breast cancer. British Journal of Surgery 83: 98-102.
- Hedman M, Bjork-Eriksson T, Brodin O, Toma-Dasu I (2013) Predictive value of modelled tumor control probability based on individual measurements of in vitro radiosensitivity and potential doubling time. Br J Radiol 86: 20130015.
- Fowler J (2010) 21 years of Biologically Effective Dose. The British Journal of Radiology 83: 554–568.
- Marcu L (2018) Radiotherapy and Clinical Radiobiology of Head and Neck Cancer. Series in Medical Physics and Biomedical Engineering. CRC Press.
- Casesnoves F (2022) Radiotherapy 3D Isodose Simulations for Wedge Filter 18 Mev-Dose [ z = 5,15cm ] with AAA Model with Breast Cancer Applications. International Journal on Research Methodologies in Physics and Chemistry (IJRPC).
- Garden A, Beadle B, Gunn G (2018) Radiotherapy for Head and Neck Cancers. Fifth Edition. Wolters Kluwer.
- Casesnoves F (2023) Radiotherapy Genetic Algorithm Pareto-Multi objective Optimization of Biological Effective Dose and Clonogens Models for Head and Neck Tumor Advanced Treatment. International Journal of Mathematics and Computer Research 11(1): 3156-3177.
- Casesnoves F (2023) Radiotherapy effective clonogens model graphical optimization approaching linear quadratic method for head and neck tumors. International Journal of Molecular Biology and Biochemistry.
- Lindblom E, Dasu A, Iuliana Toma-Dasu I (2015) Optimal fractionation in radiotherapy for non-small cell lung cancer – a modelling approach, Acta Oncologica 54: 9.
- Kaidar-Person O, Chen R (2018) Hypo fractionated and Stereotactic Radiation Therapy. Springer.
- Casesnoves F (2022) Radiotherapy Genetic Algorithm Pareto-Mult objective Optimization of Biological Effective Dose and Clonogens Models for Breast Tumor Improved Treatment. International Journal of Mathematics and Computer Research 11(1): 3102-3112.
- Wong J, Schultheiss T, Radany E (2017) Advances in Radiation Oncology. Springer.
- Huo M, Gorayski P, Pinkham M, Lehman M (2016) Australian College of General Practitioners.
- College of Radiologists UK (2019) Radiotherapy dose fractionation. Third edition. Clinical Oncology.
- Murshed M (2019) Fundamentals of radiation oncology physical, biological, and clinical aspects. Academic Press. Elsevier.
- Hedin E (2016) Estimation of clinical dose distributions for breast and lung cancer radiotherapy treatments. PhD thesis. Gothenburg University.
- Reckamp K (2016) Lung cancer, treatment and research. Springer.
- Casesnoves F (2023) Training course Stereotactic Radiotherapy and Radiosurgery in Management of Metastatic Brain Tumors. Sigulda Stereotactic, Radiosurgery and Cyberknife Hospital. International Society of Radio surgery.
- Joiner M, Kogel A (2019) Basic Clinical Radiobiology.
- Cher M, Raz A ( 2002) Prostate Cancer: New Horizons in Research and Treatment.
- Sureka C, Armpilia C (2017) Radiation Biology for Medical Physicists.
- Andisheh B, Edgren M, Belkić D, Mavroidis P, Brahme A (2013) A Comparative Analysis of Radiobiological Models for Cell Surviving Fractions at High Doses. Technology in Cancer Research and Treatment 12(2): 183-192.
- Casesnoves F (2023) Radiotherapy BED Model 2D Pareto- Multi objective Evolutionary Optimization for Prostate Cancer Hyper fractionated Treatment. Biomed J Sci & Tech Res 51(2).
- Borst G (2009) Radiotherapy for Lung Cancer.
- Trombetta M (2018) Alternate Fractionation in Radiotherapy.
- Reckamp K (2016) Lung cancer, treatment and research.
- Altmann K, Lett J (1992) Advances in radiation biology. Relative Radiation Sensitivities of Human Organ Systems.
- Casesnoves F (2022) Genetic Algorithms for Interior Comparative Optimization of Standard BCS Parameters in Selected Superconductors and High-Temperature Superconductors. Standards 2: 430-448.
- Casesnoves F (2023) Training course Stereotactic Radiotherapy and Radiosurgery in Management of Metastatic Brain Tumors. Sigulda Stereotactic, Radiosurgery and Cyberknife Hospital. International Society of Radiosurgery.
- Carini H, Fidock M, Van GA (2019) Handbook of Biomarkers and Precision Medicine. CRC Press.






























