Latent Factors Affecting Smoking Cessation Among TB and HIV Patients: Bayesian Structural Equation Modeling Approach
Vasantha Mahalingam1*, Ramesh Santhanakrishnan2, Ponnuraja Chinnaiyan1, Adhin Bhaskar1, Muniyandi Malaisamy3, Mythily Venkatesan1 and Venkatesan Perumal1
1Department of Statistics, ICMR-National Institute for Research in Tuberculosis, India
2Department of Clinical Research, ICMR-National Institute for Research in Tuberculosis, India
3Department of Health Economics, National Institute for Research in Tuberculosis, India
Submission: January 25, 2024; Published: February 15, 2024
*Corresponding author: Vasantha Mahalingam, Department of Statistics, ICMR-National Institute for Research in Tuberculosis, Chennai, India, Email id: vasanthabio@gmail.com
How to cite this article: Vasantha Mahalingam*, Ramesh Santhanakrishnan, Ponnuraja Chinnaiyan, Adhin Bhaskar, Muniyandi Malaisamy, Mythily Venkatesan and Venkatesan Peruma. Latent Factors Affecting Smoking Cessation Among TB and HIV Patients: Bayesian Structural Equation Modeling Approach. Int J Pul & Res Sci. 2024; 7(1): 555703. DOI: 10.19080/IJOPRS.2024.07.555703
Abstract
Structural Equation Model (SEM) is an advanced multivariate statistical tool for modeling latent variables and to control measurement errors. Bayesian SEM (BSEM) gives better estimates of latent variable compared to classical SEM. To our knowledge the use of BSEM approach to identify the significant latent constructs influencing quit smoking in tuberculosis (TB) and human immunodeficiency virus (HIV) patients was not studied so far. The aim of this study is to identify latent variables influencing quitting smoking in TB and HIV patients using BSEM. The data used for the study consist of 160 patients (80 TB and 80 HIV) randomised to receive smoking cessation intervention under clinical trial. The smoking status was measured after one month of intervention. The latent variables ‘reasons for smoking’ (measured by the variables work tension, family tension and pleasure while smoking) and ‘intensity of smoking’ (measured by the variables Fagerstrom score, smoking type, number of times smoking per day and smoking duration) and the information on socio-economic characteristics were considered for analyses. This study elucidates the importance of applying BSEM to assess smoking cessation in TB and HIV patients. BSEM gave the estimates indicating the latent variable ‘intensity of smoking’ had negative effect on quit smoking.
Keywords: Randomised Clinical Trial; Smoking Cessation; TB; HIV; Bayesian Structural Equation Model
Abbreviations: SEM: Structural Equation Model; BSEM: Bayesian SEM; TB: Tuberculosis; HIV: Human Immunodeficiency Virus; RCT: Randomised Controlled Clinical Trial; MDR-TB: Multidrug Resistance TB
Introduction
Structural equation models (SEMs) are advanced statistical models that represent complex relationships between latent and observed variables [1]. Latent variables are random variables which are measured indirectly through observed variable. SEM is a superior modeling tool than other techniques because of reducing measurement errors by having multiple indicators of latent variables that is free from random error. Only a few studies attempted SEM to evaluate many factors which are inter-related and cannot be easily disentangled by traditional statistical techniques [2-5].
Simulations studies have compared Bayesian estimation and frequentist estimation for SEM with small samples and advantage of Bayesian SEM (BSEM) is well documented in literature [6,7]. The BSEM is a potential tool to overcome assumption issues and robust for small sample problems [8-11]. In BSEM, the computation algorithm is based on raw observation rather than covariance matrix as in classical SEM and solved using powerful computing techniques such as Gibbs sampler and Metropolis-Hasting’s algorithms [12]. Numerous articles highlighted superiority of BSEM compared to other traditional techniques [8,9,12-16]. To our knowledge the use of BSEM to identify the significant latent constructs influencing quit smoking in tuberculosis (TB) and human immunodeficiency virus (HIV) patients was not studied so far. In the current study, we hypothesised a latent variables model using BSEM to identify the influencing factors for quit smoking in TB and HIV patients after one month of the interventions.
There is ample evidence for the association between smoking and TB, with literature showing smoking among TB patients causes morbidity and mortality. It was reported that smoking has been also associated with multidrug resistance TB (MDR-TB) [17-22]. Smokers who are infected with HIV will face more risks besides the impact of smoking. Compared to non-smoker, smokers were having poor viral and immunological response, more threat of virological rebound [23].
ICMR-National Institute for Research in Tuberculosis conducted a randomised controlled clinical trial (RCT) for quit smoking among TB and HIV patients. This trial used two interventions, one arm being standard counselling and other arm being physicians’ advice along with standard counselling to see the efficacy [24]. This was a unique opportunity to use this data to identify the latent factors influencing the quit smoking. We made an attempt to use BSEM for latent variables influencing quit smoking for TB and HIV patients and presented in this paper.
The paper is structured as follows. In section 2, we propose BSEM model for continuous and ordered categorical variables. In section 3, we provide application of BSEM for clinical trial data to identify latent variables influencing for quitting smoking in TB and HIV patients. Section 4 describes results of the BSEM model. Final section provides discussions and conclusions.
Methodology
SEM
SEM consists of the measurement equation and structural equation, the measurement equation of the SEM is defined by

where
yi = p X 1 random vector,
Λ = p X q factor loading matrix,
ωi = q X 1 factor scores vector and
∈i = (p x 1) is a random vector of error measurement
∈ ~),0(∈ΨN where Ψ∈ is a diagonal matrix.
Let  is a partition of ωi into an q1 x 1 dependent latent vector ηi and an q2 x 1 independent latent vector ξi, where ξ ~ N (0, I) and uncorrelated with ∈. The structural equation which provides the relationship between dependent latent variables and independent latent variables can be written as
is a partition of ωi into an q1 x 1 dependent latent vector ηi and an q2 x 1 independent latent vector ξi, where ξ ~ N (0, I) and uncorrelated with ∈. The structural equation which provides the relationship between dependent latent variables and independent latent variables can be written as

where,
П(q1 x q1) & )q x q(21Γ= unknown parameter matrices of regression coefficients;
δi = q1 x 1 random vector of error measurements.
ξi ~N[0, Ф], and δi ~N[0, Ψδ],
Ψδ = diagonal matrix and ξi and δi are independent [12].
Suppose, v = {x,y}, where x = {x1,...,xr} is a subset of observable continuous variables, while y = {y1,...,yr} be the remaining subset of unobservable continuous variables where p ≥ s = p-r ≥ 0. The information related with y be given as an ordered categorical vector z = {z1,...,zr}T. The latent variable are either continuous or ordered categorical manifest variables as its indicators. The relationship of y and z is defined by a set of thresholds as given bellow:

where,  and for
and for 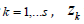 is an integral value in {0,1, …bk}. In general, we set
is an integral value in {0,1, …bk}. In general, we set  There are bk+1 categories, for kth variable that are defined by the unknown threshold αk,j. The integral values {0,1, …bk} of zk are used for identifying the categories which contain the corresponding elements in yk. These integral values are neither directly used in the posterior simulation nor in any actual computation of Bayesian analysis [12].
There are bk+1 categories, for kth variable that are defined by the unknown threshold αk,j. The integral values {0,1, …bk} of zk are used for identifying the categories which contain the corresponding elements in yk. These integral values are neither directly used in the posterior simulation nor in any actual computation of Bayesian analysis [12].
Markov Chain Monte Carlo Algorithms
In Frequentist analysis, parameters are used as constant, whereas in Bayesian analysis, parameters are taken as variables [25]. In Bayesian analysis, the prior distributions of a parameter is combined with likelihood obtained from the data to form posterior distribution of the estimates of the parameter. The Bayesian estimates of the latent variables and the parameters are estimated using Markov Chain Monte Carlo (MCMC) methods called the Gibbs sampler [26] and the Metropolis-Hastings (MH) algorithm [27,28]. MCMC algorithms creates approximations to the posterior distributions by iteratively selecting random draws in the MCMC chains. The initial draws of the estimates are mentioned as the burnin phase of the MCMC algorithms. The trace plot of the posterior draws can be utilised to monitor the convergence. The maximum number of iteration for convergence can be assessed graphically by plotting the simulated sequences of individual parameters. If converged, the parallel sequence created with diverse initial values which overlap well. The convergence can also be supervised using the Gelman-Rubin potential scaling reduction by the parallel computing in multiple MCMC chains. The parallel sequence of observations and the estimated potential scale reduction (EPSR) values of the parameters are estimated sequentially based on the starting values of the structural parameters and latent variables as the iterations proceed [29]. The ESPR values are less than 1.2 implies the convergence of the model [15].
Evaluation Criteria
The model fit of BSEM is evaluated using a posterior predictive (PP) p-value. The BSEM model is considered to have a good fit if PP p- value near to 0.5. If the PP p-value is small (approaching zero), the model is a poor fit for the data [12].
Application of BSEM to Clinical Traill Data
Data
We used secondary data from randomised controlled trial piloted at ICMR-National Institute for Research in Tuberculosis (ICMR-NIRT), Madurai Unit during March 2010 to May 2012. A total of 160 patients (80 TB patients and 80 HIV patients) aged ≥ 18 years, with either HIV or TB and with a history of current smoking (at least one cigarette in the past 1 week) were enrolled. This study was registered in the Clinical Registry of India (CTRI/2009/091/000962, 14.12.2009), approved by Scientific Advisory Committee and Institutional Ethics Committee of ICMR-NIRT, Chennai to study the efficacy of physician’s advice in quitting smoking.
Smoking Cessation intervention
The study participants were randomised to receive either intervention (Physician’s advice + counsellors’ counselling + Brochure/educative material) or control (counsellors’ counselling + Brochure/educative material) for smoking cessation. The random allocation of the intervention was stratified based on nicotine dependence, evaluated using Fagerstrom dependence scale (a score of ≤5 was considered low and > 5 was high according to the Fagerstrom scale) [24]. In the intervention group, the physician’s advice was implemented via the modified 5As strategy (Ask the patient if she/he uses tobacco, Advise her/him to quit, Assess willingness to make a quit attempt, Assist her/ him in making a quit attempt, and Arrange for follow-up contact to prevent relapse) for quit smoking with the brochure describing the guidelines for smoking cessation and counselling from a counsellor. The control group was received a brochure explaining smoking cessation guidelines and counselling from a counsellor. The observed variables in this study were education, alcoholism, type of smoking, past history of quit smoking, number of times smoking in a day, different reasons for smoking. Quitting rate at end of one month was evaluated by self-reporting of the patient and carbon monoxide monitor reading breath analysis. The quit rate was defined as smoker not smoking at month one with history of smoking abstinence for one week and a carbon monoxide concentration <10ppm at the first month [24].
Model Specification
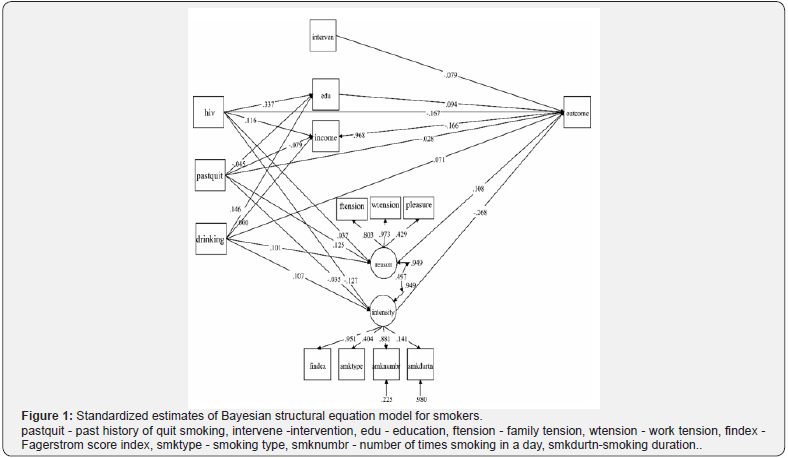
In the study, the independent variables used were Fagerstrom score, smoking type, number of times smoking in a day and smoking duration, income, intervention to quit smoking, drinking habits, past history of quit smoking, presence of HIV infection and the reasons for smoking such as pleasure, work tension and family tension. There were seven independent variables framed as two independent latent variables. The three variables pleasure, work tension and family tension were used as indicator variables for the latent variable ‘reason’ (ξ1) which was intended to address reason for smoking. The four variables Fagerstrom score, smoking type, number of times smoking and smoking duration were selected as indicator variables to address the latent variable ‘intensity’ (ξ2). The variables educations, income, intervention, drinking habits, past history of quit smoking, presence of HIV or TB infection were considered as covariates. The hypothesis of the study was that the latent variables ‘intensity’ and ‘reason’ were related to quit smoking after one month of the interventions. The hypothesis and the path diagram of SEM is given in (Figure 1). In the model of the current study, yi is 7 X 1 vector of manifest variable defining the 2 X 1 random vector of latent variables ωi. The factor loading matrix Λ is given below as

where, λij are factor loading parameters with remaining values of the matrix are fixed as one and zero in the estimation in order to achieve the model identification. The non-overlapping structure of matrix leads to two latent variables. The structural model for this study is described as
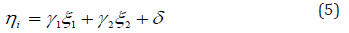
Where the distributions of δ and  are independently distributed as N [0, Ф] and
are independently distributed as N [0, Ф] and 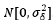 .
.
Software used
The latent class analyses were carried out using the software MPlus version 7.1. By assuming there was no prior knowledge about distributions of parameters, Mplus default prior (non-informative prior) for BSEM was used for the study.
Results
Profile of study population
Out of 160 patients, 24 patients (12 patients in each intervention group) didn’t come back after first smoking cessation visit. The remaining 136 (68 each arm) patients available after one month of intervention was considered for further analysis. The profile of study population was given in (Table 1). All the patients were observed as male with average age of 40 years with standard deviation of 8.6. Of the 136 patients, 59 (43%) were aged >40 years; literate was 111 (82%), alcohol users 109 (80%) and both cigarettes and Beedi smokers 55 (40%).

Quit rate
Overall combined analysis including both HIV and TB, the quit rate was 38% (52/136). The quit rate among the patients received physician’s advice was 41% (28/68) and in the standard counselling was 35% (24/68) though the difference in quit rate was not significant (p=0.473).
Convergence of BSEM
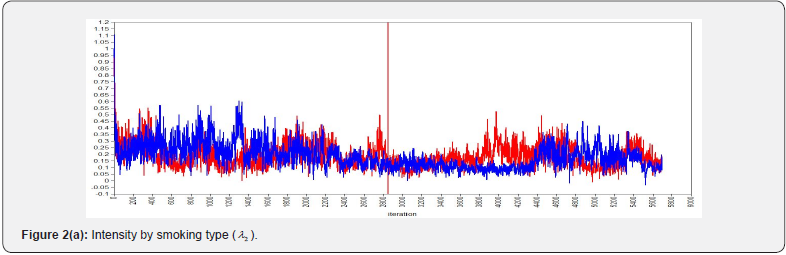
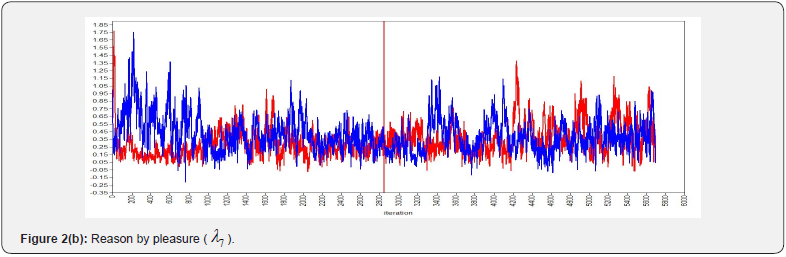
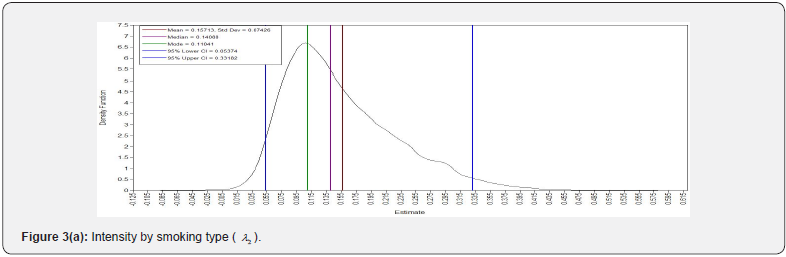
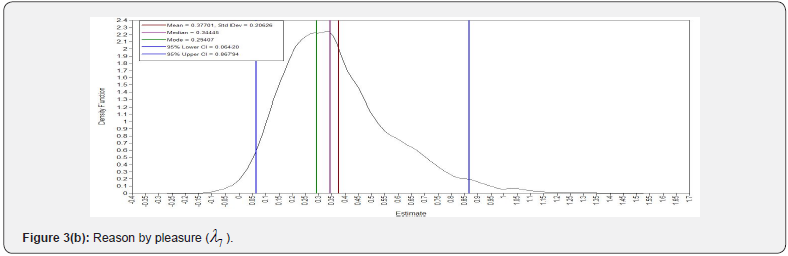
The SEM model for this dataset did not converge; hence, we conducted a BSEM model for the study. To get the Bayesian estimates of latent variable and the parameters, 3000 observations were generated after discarding the first 3000 burn-in iterations. The convergence of the sampler was verified by assessing the trace plots. The plots for a selection of the parameters and posterior distribution of kernel density are shown in (Figure 2 and 3). (Figure 2) shows convergence plots, which demonstrate tight overlapping of parameter estimates across iterations. The overlapping indicates that the parameters are converged. The posterior probability density plots in (Figure 3) which depicts that the posterior distribution of the parameters is approximating normal. ESPR values are also found to be less than 1.2 after 2,000 iterations.



Model fit of BSEM
In the current study, 42 parameters were used to estimate the influencing factors for quit smoking. The PP p-value of 0.3 for the fitted BSEM indicated the good fit of the model for the data.
BSEM model estimates
The results of Bayesian estimates attained using 3000 observations after convergence are presented in (Table 2 and 3). The posterior estimates of the parameters and their 95% posterior credible intervals are presented in (Table 2 and 3). The standardised estimate of structural equation for quit smoking is


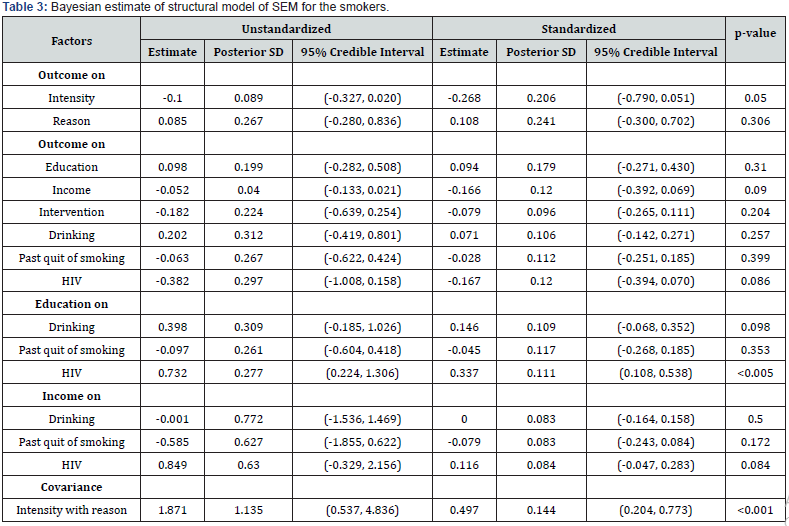
The latent variable intensity was almost significantly associated with the variable quit smoking after one month of the interventions. The estimate of intensity on quit smoking is -0.268 (p=0.05). The intensity had negative effect on the latent variable quit smoking. There was significant association between education and HIV disease (0.337, p<0.005) while drinking habits and past history of quit smoking were not associated with education as well as income. The variance between the latent variables ‘intensity’ and ‘reason’ for smoking was significantly different (0.497, p<0.001). When the smoking intensity of the patients was less, the patients had more chance to quit smoking habit (Table 3).
All the factor loadings except smoking duration were significantly associated with their corresponding latent variables. The standardized estimates of Fagerstrom score, smoking type, number of times smoking in a day and smoking duration on the latent variable intensity were as follows: 0.951 (p < 0.001), 0.404 (p < 0.005), 0.881 (p < 0.001), and 0.141 (p = 0.064). The estimates of family tension, work tension and pleasure on the latent variable ‘reason’ were 0.803 (p < 0.001), 0.973 (p < 0.001) and 0.429 (p < 0.01), respectively. The covariates drinking, past history of quit smoking was found to be insignificant with the latent variables ‘intensity’ (ξ1) and ‘reason’ (ξ2) (Table 2).
Discussion
The novel approach of the study was first of its kind to use BSEM with continuous and categorical variables in evaluating quit smoking in TB and HIV patients. The measurement and structural equations obtained from this study were useful to identify the latent variables influencing quit smoking. Bayesian SEM with non-informative prior gave the estimates indicating the latent variable ‘intensity’ of smoking was significantly negatively associated with smoking status of the patients after one month of intervention. The current study identified relationship between latent variables, intensity of smoking and reason for smoking. It was found that there was a statistically significant association between education and HIV disease and no association between intervention and quit smoking.
The current study using BSEM clearly identified that the latent variable intensity of smoking had negative effect on the outcome variable quit smoking of the patient. When the smoking intensity of the patients was less, the patients had more chance to quit smoking habit. The findings were corroborated with the findings from other previous studies using traditional methods [30-33]. This reveals that the behaviours which lead to greater cumulative exposure to tobacco products, smoking more cigarettes per day and including younger age at initiation increase risk for death and reduce the chance to quit.
BSEM was used in other settings and showed better estimates. The cross-cultural consistency of the factor structure of the Hedonic and Eudaimonic Motives for Activities (HEMA) scale was examined by BSEM showed that BSEM is more informative than the traditional SEM [34]. Similarly other studies applied BSEM to identify the factors for non-adherence to medication among hypertension patients [13], and type 2 diabetic patients with nephropathy [35]. In the current study showed that PP p- value for the model fit was 0.3 indicating that the BSEM model was found to be adequately fitting the data.
Conclusion
The Novel approach of the study was that from our knowledge we used first time BSEM to identify the latent constructs which influence quit smoking in TB and HIV patients. BSEM is powerful statistical computing tool for more accurate analysis of more complex variables.
Acknowledgement
The authors acknowledge the authorities of ICMR-National Institute for Research in Tuberculosis, Indian Council of Medical Research, Chennai for permitting us to use the data for modelling.
References
- Beran TN, Violato C (2010) Structural equation modeling in medical research: a primer. BMC Research Notes 3: 267.
- Businelle MS, Kendzor DE, Reitzel LR, Costello TJ, Cofta Woerpel L, et al. (2010) Mechanisms linking socioeconomic status to smoking cessation: a structural equation modeling approach. Health Psychology 29(3): 262-273.
- Huang C, Guo C, Yu S, Feng Y, Song J, et al. (2013) Smoking behaviours and cessation services among male physicians in China: evidence from a structural equation model. Tobacco Control 2(2): 27-33.
- Martinez SA, Beebe LA, Thompson DM, Terrell DR, Campbell JE (2018) A structural equation modeling approach to understanding pathways that connect socioeconomic status and smoking. PLoS ONE 2: 1-17.
- Sauer A, Fedewa SA, Kim J, Jemal A, Westmaas JL (2018) Educational attainment & quitting smoking: A structural equation model approach. Preventive Medicine 116: 32-39.
- Smid SC, Mcneish D, Miočević M, Schoot RV (2020) Bayesian Versus Frequentist Estimation for Structural Equation Models in Small Sample Contexts: A Systematic Review. Structural Equation Modeling: A Multidisciplinary Journal 27(1): 131-161.
- De Schoot R, Kaplan D, Denissen J, Asendorpf JB, Neyer FJ, et al. (2014) A Gentle Introduction to Bayesian Analysis: Applications to Developmental Research. Child Development 85(3): 842-60.
- Scheines R, Hoijtink H, Boomsma A (1999) Bayesian estimation and testing of structural equationmodels. Psychometrika 64: 37-52.
- Lee SY, Shi JQ (2000) Bayesian analysis of structural equation model with fixed covariates. Structural Equation Modeling 7(3): 411–430.
- Ansari A, Jedidi K, Dube LL (2002) Heterogeneous factor analysis models: A Bayesian approach. Psychometrika 67: 49-78.
- Lee S, Song X (2004) Bayesian model comparison of nonlinear structuralequation models with missing continuous and ordinal categorical data. British Journal of Mathematical and Statistical Psychology 57: 131-150.
- Lee SY (2007) Structural Equation Modeling: A Bayesian Approach. John Wiley & Sons Ltd. England.
- Lee SY, Song XY (2003) Bayesian analysis of structural equation models with dichotomous variables. Statistics in Medicines 22: 3073-3088.
- Kaplan D, Depaoli S (2012) Handbook of Structural Equation Modeling. Hoyle RH, editor. The Guilford Press.
- Muthèn LK, Muthèn BO (2017) MPlus user’s guide. Los Angeles, CA: Muthèn and Muthè Los Angeles, CA.
- Van De Schoot R, Depaoli S (2014) Bayesian analyses: Where to start and what to report. European Health Psychologist 16: 75–84.
- Altet-Gomez MN, Alcaide J, Godoy P, Romero MA (2005) Hernandez del Rey I. Clinical and epidemiological aspects of smoking and tuberculosis: a study of 13,038 cases. International Journal of Tuberculosis Lung and Disease 9(4): 430-436.
- Ariyothai N, Podhipak A, Akarasewi P, Tornee S, Smithtikarn S, et al. (2004) Cigarette smoking and its relation to pulmonary tuberculosis in adults. Southeast Asian Journal of Tropical Medicine and Public Health 35(1): 219-227.
- Barroso EC, Mota R, Santos RO, Sousa A, Barroso JB, et al. (2003) Risk factors for acquired multidrug resistant tuberculosis. Journal of Pneumologia 29: 89-97.
- Chiang CY, Slama K, Enarson DA (2007) Associations between tobacco and tuberculosis. International Journal of Tuberculosis and Lung Disease 11(3): 258-262.
- Pai M (2009) Tobacco and TB: what clinicians can and must do? J MGIMS 14: 1-6.
- Thomas A, Gopi PG, Santha T, Chandrasekaran V, Subramani R, et al. (2005) Predictors of relapse among pulmonary tuberculosis patients treated in a DOTS programme in south India. International Journal Tuberculosis Lung Disease 9(5): 556-561.
- Feldman JG, Minkoff H, Schneider MF (2006) The association of cigarette smoking with HIV prognosis among women in the HAART era-a report from the Women’s Interagency HIV Study. American Journal of Public Health 96(6): 1060-1065.
- Kumar SR, Pooranangangadevi N, Rajendran M, Mayer KH, Flanigan T, et al. (2017) Physician’s advice on quitting smoking in HIV and TB patients in south India: a randomised clinical trial. Public Health Action 7: 39-45.
- Gelman A, Stern HS, Carlin JB, Rubin DB (2004) Bayesian Data Analysis. London, England: Routledge.
- Geman S, Geman D (1984) Stochastic relaxation, Gibbs distribution and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence 6: 721-741.
- Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) Equations of state calculations by a fast-computing machine. Journal of Chemical Physics 21: 1087-1091.
- Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their application. Biometrika 57: 97-109.
- Gilks WR, Richardson S, Spiegelhalter DJ, (1996) Gelman A Inference and monitoring convergence. London: Chapman and Hall.
- Inoue-Choi M, Hartge P, Park Y, Abnet CC, Freedman ND (2019) Association Between Reductions of Number of Cigarettes Smoked per Day and Mortality Among Older Adults in the United States. American Journal of Epidemiology 188(2): 363-371.
- Jha P, Ramasundarahettige C, Landsman V, Rostron B, Thun M, et al. (2013) 21st-century hazards of smoking and benefits of cessation in the United States. New England Journal of Medicine 368(4): 341-350.
- Pirie K, Peto R, Reeves GK, Green J, Beral V (2013) Million Women Study Collaborators. The 21st century hazards of smoking and benefits of stopping: a prospective study of one million women in the UK. Lancet 381: 133-141.
- Thun MJ, Carter BD, Feskanich D, Freedman ND, Prentice R, et al. (2013) 50-year trend in smoking-related mortality in the United States. New England Journal of Medicine 368: 351-364.
- Bujacz A, Vittersø J, Huta V, Kaczmarek LD (2014) Measuring hedonia and eudaimonia as motives for activities: cross-national investigation through traditional and Bayesian structural equation modelling. Frontiers Psychology 5: 2-9.
- Song XY, Lee SY, Ng M, So WY, Chan J (2007) Bayesian analysis of structural equation models with multinomial variables and an application to type 2 diabetic nephropathy. Statistics in Medicine 26(11): 2348-2369.






























