An Empirical Regression Approach to Estimating Blood Pressure Components
Badmus NI*, Amusa SO, Akinsanya T and Okorafor U
Department of Statistics, Yaba College of Technology, Nigeria
Submission: October 05, 2017; Published: May 07, 2018
*Corresponding author: Badmus NI, Department of Statistics, Yaba College of Technology, Yaba, Lagos Nigeria, Tel: +2348033676685; Email: idowu.badmus@yabatech.edu.ng
How to cite this article: Badmus NI, Amusa SO, Akinsanya T, Okorafor U. An Empirical Regression Approach to Estimating Blood Pressure Components. 002 Int J cell Sci & mol biol. 2018; 4(4): 555643. DOI: 10.19080/IJCSMB.2018.04.555643
Abstract
In this paper, a log-linear regression model called log-beta modified weighted Wei bull regression model is constructed from Beta modified weighted Wei bull distribution through transformation (method of parameterized). The statistical properties including; moments, generating function, skewness and kurtosis were derived for the proposed model. The performance of the proposed model was determined using blood pressure components data and the maximum likelihood estimate of the model parameters was investigated by considering blood pressure components. The empirical results show that the proposed regression model provides better fit and is very useful to the analysis of real data.
Keywords: Log-beta; Log-linear regression; weighted wei bull; Regression model; Skewness; Kurtosis
Introduction
Regression models are used to predict one variable or more other variables, it provides researcher with a powerful tool, allowing predictions about past, present, or future events to be made with information about past or present events. Regression models can also be proposed in different forms in survival analysis; for instance the location-scale regression model which is frequently used in clinical trials. In this study, we propose a location-scale regression model, which will referred to as log-beta modified weighted Wei bull regression model based on a recently continuous distribution proposed by [1]. An extension of the beta weighted Wei bull distribution and some other distributions. In the last decade, in the last decade, new classes of distributions were developed based on extensions of the Wei bull distribution such as the modified Wei bull the beta Wei bull (BW) the generalized modified Wei bull distributions, the beta weighted Wei bull distribution, Some Statistical Properties of Exponentiated Weighted Wei bull Distribution, the Beta Weighted Exponential Distribution to mention but few.
The paper is divided into sections: Section 2, presented the beta modified weighted Wei bull distribution, the propose log-beta modified weighted Wei bull distribution with some of its properties and the log beta modified weighted Wei bull regression model of location-scale form. We estimation the model parameters using the method of maximum likelihood and the observed information matrix are presented in Section 3. Then, section 4 contains the application of the proposed model to blood pressure data from Army Hospital, Yaba, Lagos and compared with beta modified weighted Wei bull regression model using model selection criteria: the AIC, BIC and CAIC and finally conclusion is in section 5.
The Log-Beta Modified Weighted Wei bull (LBWMM) Distribution
The Log-Beta Modified Weighted Wei bull (LBMWW) distribution is an extension of beta modified weighted Wei bull (BMWW) distribution introduced by while the BMWW is developed from Modified Weighted Wei bull (MWW) distribution proposed by [2]. Where by both the density and it’s corresponding distribution function are given as follows:
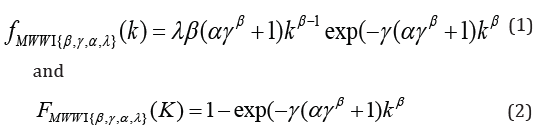
Where, λ is scale parameter, β shape parameter, α and γ are shape parameters.
Meanwhile, the density and cumulative distribution function of BMWW are also given by
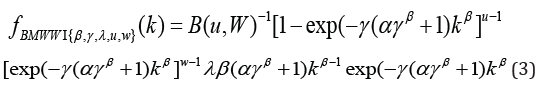
And
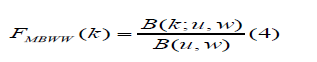
where, k >0, f (k)= d/dk F(k)andu >0,w >0 are shape parameters in addition to the existing one in the baseline (MWW) distribution, is the beta function, B(u,w) = Γ(u)Γ(w) / Γ(u + w)
Ik=(u,w)=Bk(u,w)/B(u,w) is the incomplete beta function ratio and

However, the LBMWW distribution is defined by logarithm of the BMWW random variable to give a better fitting of survival data. The MWW density function in (1) with parameters (β ,γ ,α ,λ ) > zero can be re-written in a simplified version of Wei bull as follows:
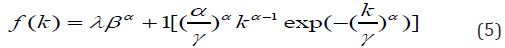
Now, we used transformation method in (5) to obtain the Log-Modified Weighted Wei bull (LMWW) distribution by setting Y =log(k)i.e.k ey ,α= 1/σ and μ log(β )i.e.β eμ and by substituting the transformation in (5), we have
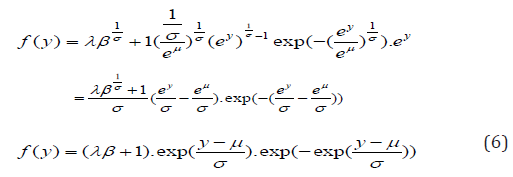
Expression (6) becomes the pdf of the LMWW distribution; and can also be written as the BMWW distribution by convoluting the beta function in equation (6) which gives

y ~ BMWW(u,w,β ,γ ,α ,λ ) Distribution, where γ is the weight parameter, α is the scale parameter, β β and λ are existing shape parameters and, u and w are shape parameters added to the existing MWW distribution; equation (7) becomes BMWW distribution.
If K is a random variable having the BMWW density function (3). Some properties of the proposed (LBMWW) distribution were obtained, and defined the random variable Y = log(k) [1, 3]. Therefore, the density function of Y had been transformed in (5). Hence, the density function of Y is defined as
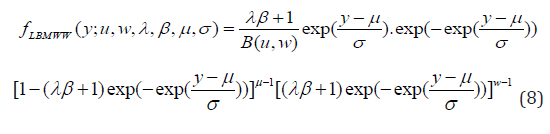
where −∞ < y < ∞,σ > 0and −∞ < μ
Equation (8) is the Log-beta modified weighted Wei bull distribution; where,μ is the location parameter, σ is a dispersion parameter, λ is the weighted parameter, β is the shape parameter and u and w are shape parameters. However, Y = log(X ) ~ LBWMM(u,w,λ,β ,μ,σ ) .
The corresponding reliability function to (8) is given by
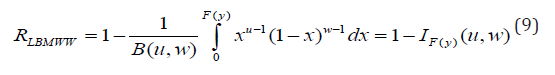
Where,

Moments and generating function
The rth ordinary moment of the LBMWW distribution is defined as
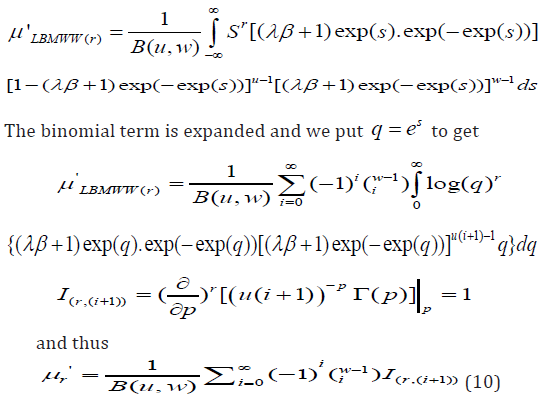
(10) leads to the moments of the LBMWW distribution; and the measures are mainly controlled by the additional shape parameters of u and w.
The moment generating function (MGF) of S, such that is M(t) = E(ets ) given by
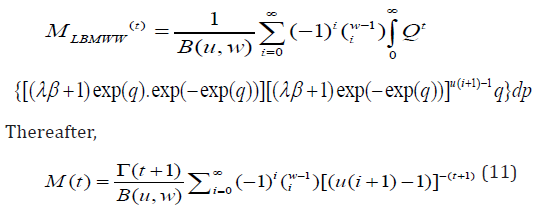
Hence, the first-four moments, the skewness and kurtosis of the LBMWW distribution were derived using the rth ordinary moment of the LBMWW as expressed in (10).
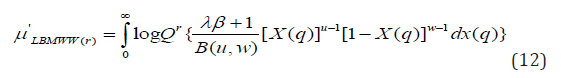
where,

where,

Furthermore, the 1st to 4th non-central momentsμr’ by substituting for r = 1, 2, 3 and 4 respectively in equation (13) it’s resulted as given below:
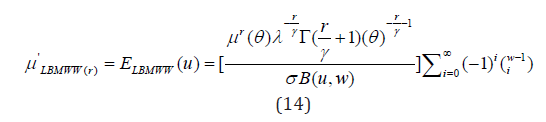
The first moment of the LBMWW is obtained from (14). Therefore, the mean, second, third and fourth moments of the LBMWW distribution are given as
Where
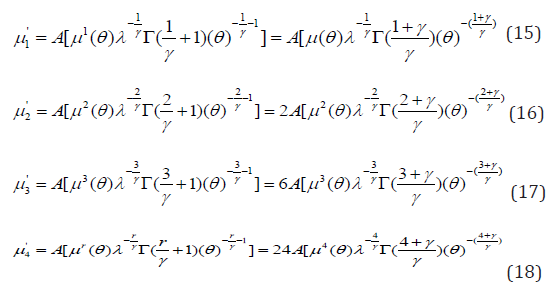
Meanwhile, measures of Skewness τ1 and excess kurtosis, τ2 are given below respectively
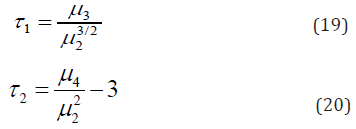
The Log-Beta Modified Weighted Wei bull Regression Model.
Here, we linked the response variable y_iand vector XiT=(xi1,.............,xip) of explanatory variables x; following location-scale regression model as given below
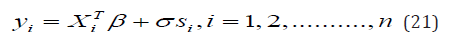
The mode has been used in literature, for example, [1,4,5,6] among others where the random error s_ihas density function
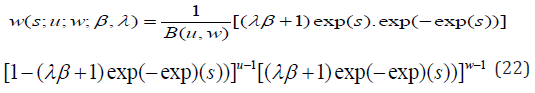
with parameters



Estimation of Model Parameter
We also consider a sample (y1,x1),...,(yn,xn) of n independent observations, where each random response is defined yi=min{log( ti), log(ci)} by We assume noninformative censoring such that the observed lifetimes and censoring times are independent. Let F and C be the sets of individuals for which is the log-life time and log-censoring, respectively. We can then apply conventional likelihood estimation techniques here. The likelihood function for the vector of parameters
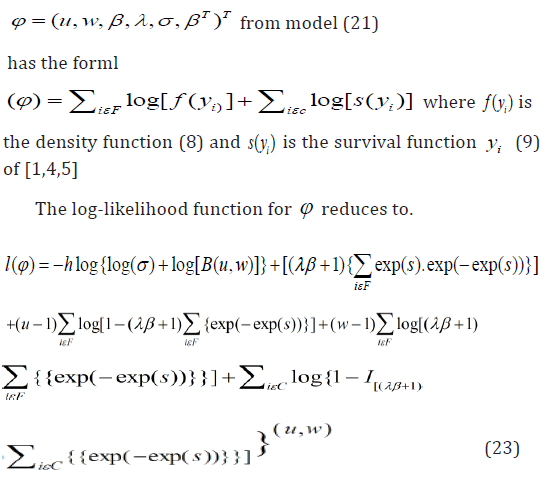
where h is the number of uncensored observations (failures) and

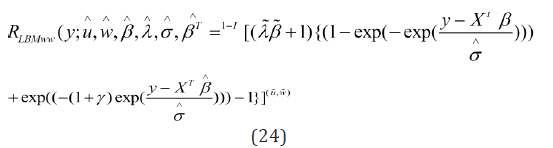
Let l(ϕ )=E[L(ϕ )] is the observed information matrix I −1(ϕ ) and the asymptotic covariance matrix of φ ̂and can be approximated by the inverse of (m+4)(m+4) observed information matrix.
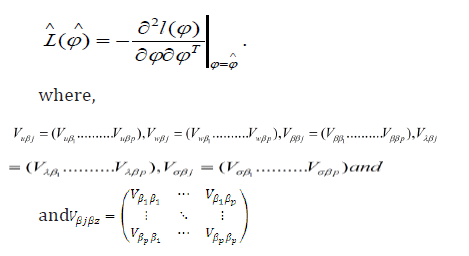
Application to Blood Pressure Data
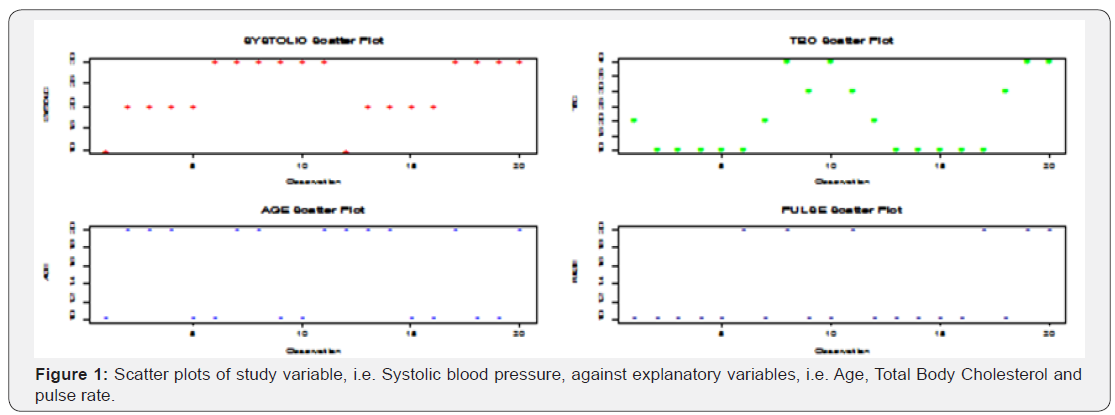
The proposed regression model was applied to blood pressure data extracted from a student project but collected from medical record department of 68 Nigerian Army reference hospital Yaba, (NARHY) Lagos. The data is referring to systolic and diastolic blood pressure for 20 patients who are diagnosed with high blood pressure and admitted. The data includes explanatory variables age, total body cholesterol and pulse rate were used for the analysis. These variables are, age during the diagnose (x1 ) (1 for 50 – 59 and 2 for 60 – 69), Total Body Cholesterol during the diagnose (x2 ) (1 for 170 – 179, 2 for 180 – 189, 3 for 190 – 199 and 4 for 200 - 209], Pulse rate during diagnos (x3 ) 1 for 80 – 89 and 2 for 90 - 99]. The model
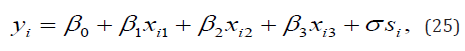
where the variable yi=log(ti) follow the log BMWW distribution given in (8), and the random errors s_ihas the density function (21), i =1,..........., 20 . For MLEs, we used the procedure NL Mixed in SAS and R code to compute model parameters and data exploratory analysis. Iterative maximization of the logarithm of the likelihood function (23) starts with initial values for β ,λ and σ taken from the fit of the LMWW regression model with u =W =1 .
Exploratory Data Analysis (EDA)
Table 1, Figures 1-3.

Summary of the Analysis
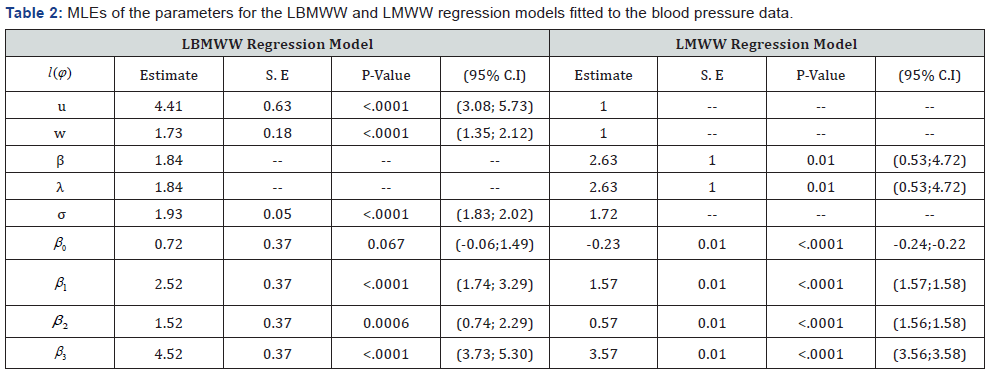
Table 2
Discussion
The scatter plot of exploratory data analysis against each of the explanatory variables was displayed in Figure 1 & 2 contains the systolic blood pressure plot against the individuals, while Figure 3 time line plot, Normal Q-Q plot, Box-plot, histogram plot, density plot, ecdf plot, showed the empirical density plots and cumulative distribution plot respectively.
Table 1 contains the MLEs of the parameters for the LBMWW and LMWW regression models fitted to the blood pressure data. The LR statistic for testing the hypotheses H0 : u = w =1 versus H1 : H0 is not true. However, we also compared the LMWW and LBMWW regression models d = 2(−91.9 − (−121.3)) = 58.8 with (p-value < 0:0001) and this favored the LBMWW model. The LBMWW model had two additional parameters and it became more flexible to fit the data, and all explanatory variables in the fitted LBMWW regression model are significant at 5%.
Furthermore, Table 2 consists the Akaike Information Criterion (AIC), Corrected Akaike’s Information Criterion (AICc) given by −2log lik + 2 p + 2 p( p +1) / (n − p −1) where (p is the number of parameters in the model and n is the number of observations used in the model), and Bayesian Information Criterion(BIC) to compare the LBMWW and LMWW. Then, lower values of the AIC, AICc and BIC indicate the most efficient model. The LBMWW regression model performs better than LMWW irrespective of the criteria and it can be used in the analysis of these data. Therefore, the proposed model is a great alternative to model survival data.
The regression component of the model was estimated as [7,8]
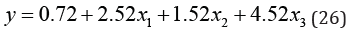
Equation (26) could be interpreted as follows:
The estimated β s (parameters of the regression model) of the proposed model in Table 1 above are positive. There will be an increase of in y for a unit change in x1 when variables x2 andx3 are held fixed and an increase of in y for a unit change in x2 when variables x1 andx3 are held fixed. Again, there would be an increase of in y for a unit change in 3 x when variables are held fixed (Table 3).

Conclusion
A new log-beta modified weighted Wei bull (LBMWW) distribution and some of it properties were properly derived. We extend the LBMWW to regression model using location-scale regression model method. Then, we discussed and obtained the estimation procedure by the method of maximum likelihood (MLEs) and information matrix. The model was applied to a cancer of the heart data and the values of AIC, AICc and BIC in the proposed Log-Beta Modified Weighted Wei bull Regression Model were respectively less than log modified weighted Wei bull regression models. Therefore, the developed LBMWW regression model provided a better fit than and has lowest AICc, AIC and BIC respectively. Therefore, Log-Beta Modified Weighted Wei bull Regression Model is more flexible and performs more efficient than Log Modified Weighted Wei bull Regressions Models.
References
- Badmus NI, Bamiduro AT, Akingbade AA, Animasaun R, Monsuru A (2016) Estimation of Parameters in Generalised Modified Weighted Wei bull Distribution. International Journal of Science and Society, Yabatech 4: 211–223.
- Aleem M, Sufyan M, Khan NS (2013) A class of Modified Weighted Wei bull Distribution and its Properties. America Review of Mathematics and Statistics 1(1): 29-37.
- Ortega EMM, Cordeiro GM, Carrasco JMF (2009) The Log-Generalized Modified Wei bull Regression Model. Brazilian Journal of Probability and Statistics 25(1): 64-89.
- Cancho VG, Ortega EMM, Bolfarine H (2009) The Log-Exponentiated- Weibull regression models with cure rate: Local influence and residual analysis. Journal of Data Science 7: 433-458.
- Pescim RR, Demetrio CGB, Cordeiro GM, Ortega EMM, Urbano MR (2013) The log-beta generalized half-normal distribution. Journal of Statistical Theory and Applications 12(4): 330-347.
- Mahmoud RM, EL- Sheikh AA, Morad NA, Ahmad MAM (2015) Log- Beta Log-Logistic Regression Model. International Journal of Sciences: Basic and Applied Research 22(2): 389-405.
- Pascoa MAR, De Paiva CMM, Cordeiro GM, Ortega EMM (2013) The Log-Kumara swamy Generalized Gamma Regression Model with Application to Chemical Dependency Data. Journal of Data Science 11: 781-818.
- Ortega EMM, Cordeiro GM, Kattan MW (2013) The log-beta Wei bull regression model with application to predict recurrence of prostate cancer. Regular Article, Statistical Paper 54(1): 113-132.






























