Developing the General Drug Disposition Equation in Linear Pharmacokinetics
Sunandan Dey*
Department of Pharmacy, University of Rajshahi, Bangladesh
Submission: July 29, 2021; Published: September 13, 2021
*Corresponding author: Sunandan Dey, Department of Pharmacy, University of Rajshahi, Bangladesh
How to cite this article:Sunandan D. Developing the General Drug Disposition Equation in Linear Pharmacokinetics. Glob J Pharmaceu Sci. 2021; 8(5): 555750. DOI: 10.19080/GJPPS.2021.08.555750.
Abstract
This mathematical observation deals with for the first time regarding the application of Mahgoub transform 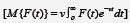 to predict the general disposition correlation in pharmacokinetics. A general drug disposition formula is developed for the n linear mammillary compartment model along with elimination occurring from every compartment. It is obviously plausible to extract the equation for the central compartment with respect to any linear pharmacokinetics. The obtaining mathematical expression predicts the fate of the intravenous input drug in the mammillary body. To be sum up, by using this presented equation, most drug disposition kinetics can be solved easily. Thus, it is cleared that this mathematical method is obviously helpful to observe the providential information in the computational biology field with the starting point in pharmacokinetics..
to predict the general disposition correlation in pharmacokinetics. A general drug disposition formula is developed for the n linear mammillary compartment model along with elimination occurring from every compartment. It is obviously plausible to extract the equation for the central compartment with respect to any linear pharmacokinetics. The obtaining mathematical expression predicts the fate of the intravenous input drug in the mammillary body. To be sum up, by using this presented equation, most drug disposition kinetics can be solved easily. Thus, it is cleared that this mathematical method is obviously helpful to observe the providential information in the computational biology field with the starting point in pharmacokinetics..
Keywords: Compartment model; Mahgoub transform; Pharmacokinetics; Rate constants
Introduction
It is obvious that in pharmacokinetics as well as in mathematical biology we often get linear differential equation, integral, and Integro differential equations, stochastic equations, and others [1-2]. Differential equations often arise in mathematical biology such as growth, and decay problems, pharmacokinetic problems, and the other computational field. The linear and nonlinear pharmacokinetic models in biopharmaceutics are used to predict the fate of the input drug to a mammillary body. In linear pharmacokinetics, simple first order kinetics is used to describe the drug disposition and action. It is also assumed in linear pharmacokinetics [3-4] that the pharmacokinetic parameters do not change for a drug when different dose or multiple doses are applied. So, it is cleared that in linear mammillary pharmacokinetic model, the numerical values of the estimated pharmacokinetic parameters are inevitable to predict the biological half-life, volume of distribution, cmax, tmax. These are analyzed through experimental data observed from plasma to estimate the effective concentration of the drug to heal diseases of the patient. The determined value of biological half-life i.e., elimination half- life (t1/2) is a must to predict the dosage regimen (dose and dosing intervals) for multiple dosage-regimen drug delivery system [5]. It is certified that 97% of the bioavailable drug is eliminated from the body after 5t1/2. Therefore, in multiple-regimens drug delivery system, the t1/2 is an inevitable factor to avoid drug accumulation in the body which produces toxic effect. According to the physicochemical properties of a drug, it may distribute in the mammillary body following one or, two or, three or multi compartment pharmacokinetic model. We developed a mathematical expression for the n linear pharmacokinetic model. This observation is helpful to predict the biological as well as physicochemical parameters of the administered drug through mathematical analysis of the experimental data. Besides, mathematics is an inseparable part of the pharmacokinetics, computational biology modeling as well. As for example, we generally use Laplace transform [6] to solve the differential equations in computational biology problems and pharmacokinetic as well. We also can use the Mahgoub transform mathematical method to solve this problem. Therefore, application of the Mahgoub transform [7] obviously assists to solve many biology related mathematical problems, precisely and correctly. In the present study, we mathematically deduce a general drug disposition correlation for the central compartment in case of linear multi compartment pharmacokinetic model, from which, it is successful that the drug disposition mathematical relationship with respect to variations of compartment model (one, or two, or three, or n) easily extracted precisely and clearly.
It is hardly found the application of Mahgoub transform [7] in computational biology. Thus, it initiates the precise application of Mahgoub transform in pharmacokinetics and mathematical biology as well.
Theory and Discussion
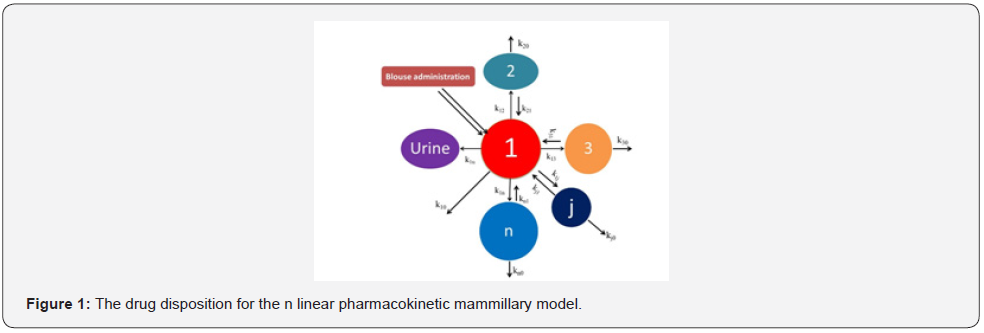
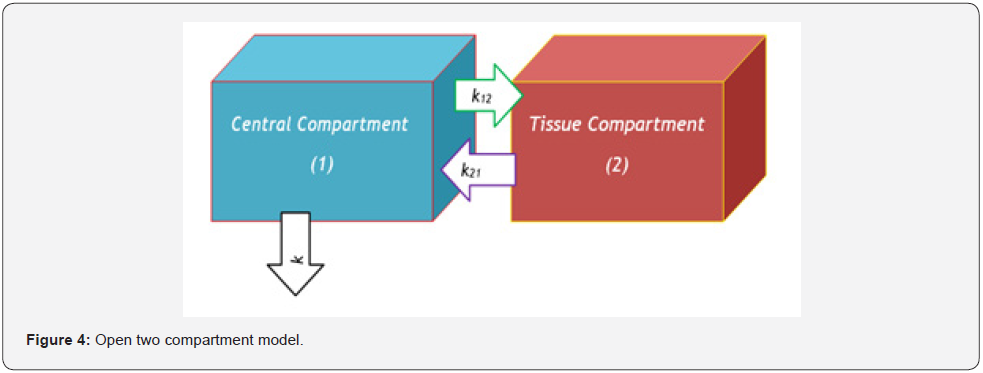
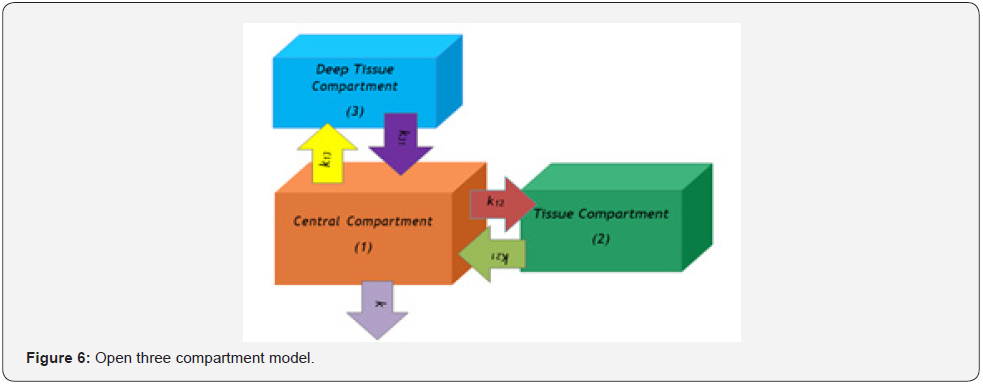
According to mammillary compartment model [8], when a drug is administered as an intravenous bolus dose, the entire drug is present in central compartment (plasma compartment) initially i.e., time is zero. Them it starts to distribute from central compartment (plasma compartment) and transports to peripheral compartment (Figure 1) for moving to the site of drug action and gives pharmacological response. Mammillary compartment model may be one compartment model (Figure 2), two Compartment model (Figure 3 & 4), three compartment model (Figure 5 & 6), as well as multi compartment model (Figure 1) respectively.

Methodology
We have derived the relationships by applying Mahgoub
Transform and Mahgoub Inverse Transform [9]. Mahgoub
transform H = H(v) of a function F = F(t) is defined by
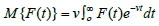 . The integral is evaluated with respect to t,so the limits are substituted. The is left are in terms of v or 1. If
M{F(t)} = H(v) then F(t) is called the inverse Mahgoub transform
of H(v) and mathematically it is defined as F(t) = M-1{H(v)}, where M-1 is the inverse Mahgoub transform operator. We have that H(e-kt)
= v/(v+k), H(1) = 1, written in the inverse transform notations,
M-1[v/(v+k)] = e-kt ; M-1(1) = 1, respectively. If a function F = F(t),
the transform of its derivative F’ can be expressed in terms of the
Mahgoub transform of: M{F’(t)} = vH(v) - vF(0).
. The integral is evaluated with respect to t,so the limits are substituted. The is left are in terms of v or 1. If
M{F(t)} = H(v) then F(t) is called the inverse Mahgoub transform
of H(v) and mathematically it is defined as F(t) = M-1{H(v)}, where M-1 is the inverse Mahgoub transform operator. We have that H(e-kt)
= v/(v+k), H(1) = 1, written in the inverse transform notations,
M-1[v/(v+k)] = e-kt ; M-1(1) = 1, respectively. If a function F = F(t),
the transform of its derivative F’ can be expressed in terms of the
Mahgoub transform of: M{F’(t)} = vH(v) - vF(0).
Proof
According to pharmacokinetic model (Figure 1).
dc1/dt = - k11c1 + k21c2 + k31c3 + ………… + kn1cn
dc2/dt = k12c1 - k22c2
dc3/dt = k13c1 - k33c3
……………………………
……………………………
dcn/dt = k1nc1 - knncn
here, c1 is concentration of drug in central compartment (plasma compartment); c2, c3………….,cn are the concentration of drug in peripheral compartments respectively at time t and kij is the first order rate constants. Besides, kii is the sum of the exit rate constants from compartments i.
Initial conditions: At time, t is zero
c1(0) = C0, c2(0) = c3(0) = …………= cn(0) = 0
Mahgoub transform for the mathematical model,
vH1(v)-vC0 = - k11H1(v)+k21H2(v)+k31H3(v)+………. + kn1Hn(v)
vH2(v) = k12H1(v) - k22H2(v); Or H2(v) = k12H1(v)/(v+k11)
vH3(v) = k13H1(v) - k33H3(v); Or, H3(v) = k13H1(v)/(v + k22)
……………………………………
…………………………………….
vHn(v) = k1nH1(v) - knnHn(v); Or, Hn(v) = k1nH1(v)/(v + knn)
Therefore,
H1(v) [(v+k11) - k12k21/(v+k22) - k13k31/(v+k33) - ……. - kn1k1n/(v + knn)] = vC0
Or,
H1(v)[(v+k11) (v+k22) (v+k33) …. (v+knn) - k12k21(v+k33) …… (v+knn) - k13k31(v+k22) ……. (v+knn) - …………. - k1nkn1(v+k22) (v+k33) ………] =(v+k22) (v+k33) ………(v+knn) vC0
Or
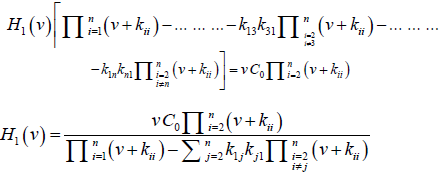
Therefore,H(v)=C0×(general disposition equation)
1. Case-1: When the drug is administered intravenously as a bolus dose that follows open one compartment model (Figure 2).
Therefore, H(v) = C0 × (general disposition equation)
2. Case 1: When the drug is administered intravenously as a bolus dose that follows open one compartment model (Figure 2)
Let the intravenous bolus dose of a drug D0 be administered to a mammillary body. The initial plasma concentration of the drug is C0. The drug is eliminated from the central compartment at a rate constant k. Here,
k11 = k [since, n = 1]
H1(v) = C0v/(v+k),
Or, C(t) = C0e-kt…………(2)
3. Case 2: When the intravenous administered drug follows open two Compartment model (Figure 4).
If the intravenous injected dose is D0, the drug is distributed in the peripheral compartment following open two compartment model, the pharmacokinetic rate constants are k12, k21 and drug is eliminated from the central compartment at a rate constant k. Now, we get from the general mathematical expression (n = 2),
k11 = k+k12, k22 = k21
[(v+k12+k)(v+k21) – k12k21] H1(v) = v(v+k21)C0
Or, [v2+(k+k12+k21)v+kk21] H1(v)= v(v+k21)C0
Now, let k+k12+k21 = a+b, kk21 = ab
So, we get that, H1(v) = v(v+k21)C0 /{(v+a)(v+b)}
Or, H1(v) = C0[v(a-k21) /{(a-b)(v+a)} + v(k21-b)/{(a-b)(v+b)}]
Or, H1(v) = {C0(a-k21)/(a-b)}v/(v+a) + {C0(k21-b)/(a-b)}v/ (v+b)}
By using inverse Mahgoub transform,
C’(t) = Ae-at + Be-bt (3)
where, A = C0(a-k21)/(a-b); B = C0(k21-b)/(a-b)
k+k12+k21 = a+b, kk21 = ab
4. Case 3: When the intravenously injected drug follows open three compartment model (Figure 6).
If the intravenous injected dose is D0, the drug is distributed in the peripheral compartment following open three compartment model, the pharmacokinetic rate constants are k12, k21, k13, k31 and drug is eliminated from the central compartment at a rate constant k. We get from the general equation (n = 3),
Here,
k11 = k+k12+k13, k22 = k21, k33 = k31
Or, [v3+(k+k12+k21+k13+k31)v2+(kk21+k21k31+kk31+k12k31+k13k21) v+kk21k31]H1(v)=vC0(v+k21)(v+k 31)
If, k+k12+k21+k13+k31 is p+q+r; kk21+k21k31+kk31+k12k31+k13k21 is pq+qr+rp, and kk21k31 is pqr
So, we get that, [v3+(p+q+r)v2+(pq+qr+rp)v+pqr] H1(v)=v(v+k21)(v+k31)C0
Or,H1(v)=v(v+k21)(v+k31)C0/{(v+p)(v+q)(v+r)}
Or, H1(v) = Pv/(v+p) + Qv/(v+q) + Rv/(v+r)
Here,
P=C0(p-k21)(p-k31)/{(p-q)(p-r)}, Q=C0(q-k21)(q-k31)/{(q-p) (q-r)}, R=C0(r-k21)(r-k31)/{(r-p)(r-q)}
Hence, C”(t) = Pe-pt + Qe-qt + Re-rt…………… (4)
k = pqr(P+Q+R)/(Pqr+Qrp+Rpq)
Calculation and Results
According to pharmacokinetic compartment model solution [10-15].
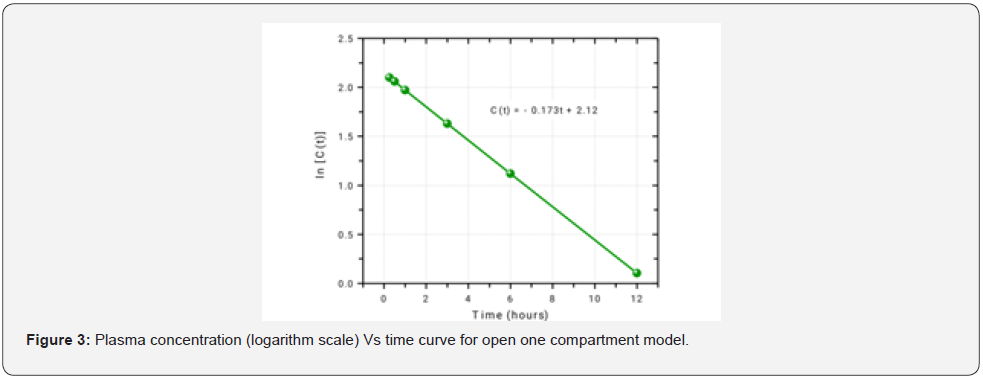
For one compartment open model (Figure 3),
k = 0.173h-1.
For two compartments model (Figure 5),
= 52; B = 18; a = 1.39; b = 0.135; k = 0.41h-1; k12 = 0.657h-1;k21 = 0.458h-1
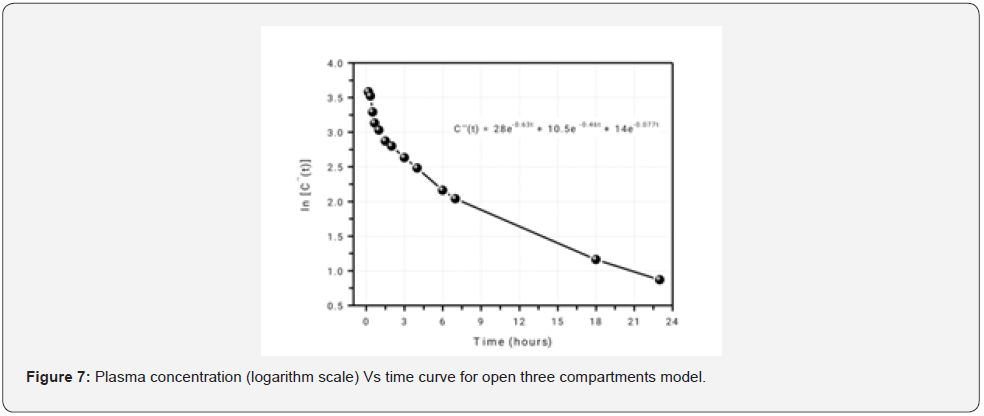
For three compartments model (Figure 7)
P = 28; Q = 10.5; R=14; p = 0.63; q = 0.46; r = 0.077; k = 0.21h-1; k12 = 0.01h-1; k21 = 0.52h-1; k13 = 0.14h-1; k31 = 0.18h-1
Conclusion
The mathematical expressions are derived from the general drug disposition equation for the central compartment in n linear compartment model ([C(t) = C0e-kt], [C’(t) = Ae-at + Be-bt], [C”(t) = Pe-pt + Qe-qt + Re-rt]). These mathematical expressions can predict the drug concentration in plasma compartment for one, two, and three compartment open model, respectively in the mammillary body. We can also predict the numerical value of pharmacokinetic factors (k12, k21, k, k13, k31) through the observation of various mathematical hybrid constants (p, q, r, P, Q, R, a, b, A, B) for the respective compartment model. So, it is cleared that this mathematical observation is successful to predict intuitive information about the bioavailable drug disposition for n-compartment mammillary model. Thus, this mathematical method initiates a successful point of view to observe the providential information in the computational biology field as well as in pharmacokinetics.
Declaration of Interests
The author declares no competing financial and non-financial interests.
Acknowledgments
The author would like to acknowledge the Rajdhani University, Rajshahi-6205, Bangladesh for providing computing facilities.
References
- Edward Batschelet (1966) The application of mathematics to biological problems Bioscience p. 22-24
- DS Jones, Michael Plank, BD Sleeman (2009) Differential equations and mathematical biology, CRC press.
- Mager, DE, Jusko WJ (2001) General Pharmacokinetic Model for Drugs Exhibiting Target Mediated Drug Disposition. J Pharmacokinet Pharmacodyn 28(6): 507-532.
- Panos Macheras, Athanassios Iliadis (2016) Modeling in biopharmaceutics, pharmacokinetics and pharmacodynamics: homogeneous and heterogeneous approaches. Springer.
- Jogarao VSG, William JJ (2001) Role of dosage regimen in controlling indirect pharmacodynamic responses, Advanced drug delivery reviews 46 (1-3): 45-57.
- Montri T, Sasitorn P (2010) The numerical solutions of differential transform method and the Laplace transform method for a system of differential equations, Nonlinear Analysis: Hybrid Systems 4(3): 425-431.
- Mahgoub MAM, Alshikh AA (2017) An application of new transform “Mahgoub Transform” to partial differential equations. Mathematical theory and Modeling 7(1): 7-9.
- Leslie ZB (1972) General treatment of linear mammillary models with elimination from any compartment as used in pharmacokinetics, Journal of Pharmaceutical Sciences 61(4): 536-541.
- Sudhanshu A, Nidhi S, Raman C, Anjana RG, Astha K (2018) A new application of Mahgoub transform for solving linear ordinary differential equations with variable coefficients, Journal of Computer and Mathematical Sciences 9(6): 520-525.
- Leon Shargel, Andrew BC Yu, Susanna WP (2017) Applied biopharmaceutics & pharmacokinetics 7th
- P Macheras (1987) Method of residuals: Estimation of absorption and elimination rate constants having comparable values Biopharmaceutics & drug disposition 8(1): 47-56.
- Richard NU (2004) Calculating the hybrid (macro) rate constants of a three- compartment mamillary pharmacokinetic model from known micro-rate constants, Journal of Pharmacological and Toxicological Methods 49(1): 65-68.
- Beyer WH (1987) CRC handbook of mathematical sciences. Boca Raton FL. CRC Press.
- Tackley RM, Lewis GTR, Prys Roberts C, Boaden RW, Dixon J, et al. (1989) Computer controlled infusion of propofol. British Journal of Anaesthesia 62(1): 46-53.
- Wagner JG (1975) Fundamentals of clinical pharmacokinetics. Hamilton IL Drug Intelligence Publications.






























