Research Article

Second Law Analyses of Forced Convection of Low-Reynolds-Number Slip Flow of Nanofluid Inside a Microchannel with Square Impediments

Ahmad Ababaei and Mahmoud Abbaszadeh*

Department of Mechanical Engineering, University of Kashan, Iran

Submission: February 15, 2017; Published: March 15, 2017

*Corresponding author: Mahmoud Abbaszadeh, Department of Mechanical Engineering, University of Kashan, Iran;Email: abbaszadeh.mahmoud@gmail.com

How to cite this article: Ahmad A , Mahmoud A . Second Law Analyses of Forced Convection of Low-Reynolds-Number Slip Flow of Nanofluid Inside a Microchannel with Square Impediments. Glob J Nano. 2017; 1(4): 555567. DOI: 10.19080/GJN.2017.01.555567

Abstract

In this study, the Finite Volume Method is employed in order to investigate the flow field, heat transfer and entropy generation of forced convection of Al2O3-water nanofluid in a parallel plate microchannel. Four square impediments are placed inside the microchannel to enhance mixing of nanofluid. The governing equations, which are accompanied with the slip velocity and temperature jump boundary conditions, are solved by SIMPLER algorithm. The study is conducted for the Reynolds numbers in the range of ≤0.1 Re ≤10, Knudsen numbers ranging of 0≤ Kn ≤0.1 and volume fraction of nanoparticles ranging of 0 ≤ ϕ ≤3%. The results show that by increasing the volume fraction of nanoparticles or the Reynolds number, the average Nusselt number and the total entropy generation augment. Furthermore, as the Knudsen number increases, both the average Nusselt number and the total entropy generation rate decrease.

Keywords: Entropy generation; Microchannel; Square impediment; Al2O3-water nanofluid; Temperature-dependent; Slip velocity; Temperature jump

Introduction

As time goes by, it is incontrovertibility axiomatic that optimization heat transfer in micro-sized devices is a crucial milestone in engineering and industrial applications. It is very important to understand that the fluid flow and heat transfer characteristics in these micro-sized devices have to be optimized in order to gain better designs. One of the most important microscaled systems is microchannel which is used in numerous applications including electronic industry, infrared detectors, integrated circuits boards, laser-diode arrays, insulation design, biological systems, heat exchanger and other compact products with high transient thermal loads. An issue of concern in these devices is the very large heat transfer surface-to-volume proportion in which resulted high compactness and effectiveness of heat removal. So, a deeply understanding of the elaborate micro-scale transport phenomena, the dynamics of fluids and the single phase forced convective heat transfer in microchannels is very important for designers. During the last two decades, a plethora of researches have focused on disparate applications of microchannels in engineering [1-6]. For the first time in 1981 Tuckerman and Pease [7] painstakingly examined the fluid flow and heat transfer in micro-scaled size. Hettiarachchi et al. [8] employed the Finite Volume Method to numerically study the three-dimensional slip flow and heat transfer in a rectangular microchannel.

They found that the entrance length increases with the Knudsen number. They also observed that the slip velocity increases the Nusselt number whereas the temperature jump results in a decrease of the Nusselt number, and their combined effect may increase or decrease the heat transfer. In a numerical study, Shams et al. [9] explored a laminar flow in a rhombus microchannel considering slip and temperature jump boundary conditions. Akbarinia et al. [10] scrutinized the forced convection fluid flow and heat transfer of Al2O3-water nanofluid in a two-dimensional rectangular microchannel at low Reynolds numbers. According to their results, increasing nanoparticles concentration at constant Reynolds numbers is not the main reason for the maximum augmentation of the Nusselt number, but it happens by increasing the inlet velocity to reach a constant Reynolds number. More recently, Karimipour [11] numerically simulated the forced convection and heat transfer of water-Cu, water-Ag, and water-Al2O3 nanofluids in a microchannel considering slip velocity and temperature jump boundary conditions at surfaces. A new model to estimate the Nusselt number was correlated. His results also indicated that higher values of slip coefficient results in more slip velocity and temperature jump, and less Nusselt number. Ebrahimi et al. [12] employed the finite volume method and SIMPLEC algorithm to numerically investigate the liquid flow and conjugated heat transfer performance in rectangular microchannels equipped with longitudinal vortex generators and filled with deionized- water. They showed that heat transfer augments with the Reynolds number.

The aspect of entropy generation, which is anchored in the Second Law of Thermodynamics, is associated with thermodynamic irreversibility's, which is common in all types of heat transfer processes. Therefore, due to its determining function on clarifying the quantitative measurement of potential work as well as exergy, entropy generation must be considered in solving convection problems. Numerous researches in the last decade were devoted to the irreversibility analysis in microchannels [13-16]. Hooman [17] explored the role of entropy generation on the forced convection heat transfer in micro-electro-mechanical systems (MEMS) in the slip-flow regime. Two types of cross-sections, parallel plates and micropipe, were considered. The effects of geometric parameters, temperature jump, and viscosity dissipation were also examined on the fluid flow and heat transfer. Sohel et al. [18] investigated the entropy generation inside the microchannel and mini channel. They used water and ethylene glycol as the base fluids, and [19] Al2O3 and Cu nanoparticles. They found that the rates of entropy generation for copper and alumina nanoparticles are identical, but these rates change when different base fluids are used. In addition, they showed that water generates much lower entropy rather than ethylene glycol because of its higher thermal conductivity. A numerical simulation to study flow field, heat transfer, and entropy generation in a ribbed microchannel was conducted by Pourmahmoud et al. [19].

They explored the effect of different parameters such as the Reynolds number, rib height, and wall heat flux on the entropy generation. They showed that the Reynolds number and heat flux control the optimum rib height and minimum total entropy generation rate. Recently, Hajialigol et al. [20] performed a numerical simulation to study mixed convection and entropy generation of water-Al2O3 nanofluid in a three-dimensional microchannel in the presence of magnetic field. According to their results, heat transfer component of entropy generation decreases as the strength of the magnetic field augments, while both friction and magnetic component of entropy generation increase. Moreover, they reported that by increasing the magnetic field strength or nanoparticles volume fraction, the total entropy generation diminishes.

Conventional fluids restrict the heat transfer rate due to their low thermal conductivity. Therefore, in order to intensify the heat transfer rate dilute suspensions of nanoparticles in liquids, called nanofluids, were introduced as an innovative solution. Over the past few years, quite a few theoretical papers appeared, providing correlations to estimate nanofluid properties and models describing the underlying physics of enlarged thermal conductivities for different nanoparticle-and-liquid pairings [21-24]. Aminossadati et al. [25] performed a numerical study to investigate the forced convection flow through a horizontal microchannel filled with water-Al2O3 nanofluid in the presence of a magnetic field. They analyzed the effects of relevant parameters such as Reynolds and Hartmann numbers and volume fraction of nanoparticles on flow field and heat transfer. Based upon their results, the average Nusselt number increases with the volume fraction in all considered Reynolds and Hartmann numbers. They also reported that the heat transfer increases with the Hartmann number at all Reynolds numbers. Flow field and heat transfer of a non-Newtonian nanofluid in two-dimensional microchannel with and without micromixers is investigated by Islami et al. [26]. They utilized CuO nanoparticles suspended in non-Newtonian base fluid of 0.5 wt% aqueous solution of Carboxymethyl Cellulose. They concluded that the presence of micromixers increases the local heat transfer and friction coefficients.

The flow field, heat transfer and entropy generation of Cu- water nanofluid under a magnetic field in a trapezoidal enclosure is numerically investigated by Aghaei et al. [27]. They showed that the average Nusselt number and total entropy generation augment by increasing the volume fraction of nanoparticles. In addition, by increasing the Hartmann number, the average Nusselt number and the total entropy generation decrease.

These studies have shown that nanofluids could be utilized in different applications in engineering, cooling of various devices, etc. However, a novel application of nanofluids could be found in modern medicine. For example, where the nanodrugs are mixed in microchannels for controlled delivery with bio-MEMS [28]. Such applications, like biological processing, lab on the chips, micro-reactors, and fuel cells, require rapid and complete mixing of fluid.

Microchannel flows, due to very low flow rate, are characterized by very low Reynolds numbers. Owing to the predominantly laminar flow, it is difficult to achieve effective mixing fluids. If the mixing is obtained primarily by a diffusion mechanism, then fast mixing becomes impossible. Hence microfluidic mixing is a very challenging problem because it requires fast and efficient mixing of low diffusivity fluids [29]. In general, micromixers are classified into two types: active and passive. In order to achieve rapid mixing in passive micromixers, obstacle structures were inserted into microchannels to enhance the advection effect via splitting, stretching, breaking and folding of liquid flows. Chung et al. [30] designed, fabricated and simulated a passive micromixer which contains some baffles with different arrangement. Alam and Kim [31] numerically investigated the mixing of fluids in a microchannel with grooves in its side walls and found out that it has better mixing performance than smooth channel at Re > 10. Islami et al. [32] numerically investigated the heat transfer of water-alumina nanofluid flow in microchannels containing micromixer. The results showed that the presence of micromixers increases heat transfer. It was also found that the main mechanism of enhancing heat transfer or mixing is the recirculation zones that are created behind the micromixers. The size of these zones increases with Reynolds number and baffle height.

In a view of proliferation literature, it is self-evident that optimization of nanofluid flow inside a parallel plate microchannel by means of entropy generation has not received any attention and a study about it still remains to be carried out. Therefore, in this investigation, the impact of four square blocks on flow pattern, temperature distribution and entropy generation of Al2O3-water nanofluid through a microchannel is investigated numerically by considering slip velocity and temperature jump boundary conditions.

Problem formulation

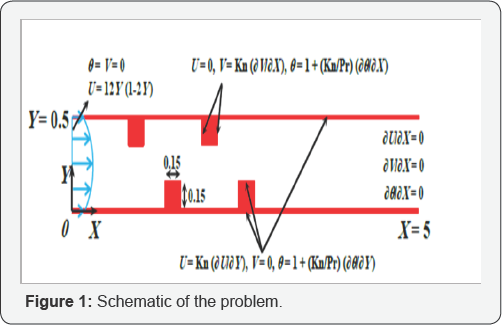
The geometry and boundary conditions are shown in (Figure 1). The proportion of the length to the height of the microchannel is ten. The height of the microchannel is half of its unit length, hence Dh = 2 x 0.5L = L. Both the upper and lower plates of microchannel as well as impediments are hot and the slip velocity and temperature jump boundary conditions are imposed on them. The inlet flow of Al2O3-water nanofluid is cold.

The governing equations of the conservation of mass, momentum and energy for the two-dimensional, steady, and laminar forced convection of the nanofluid flow, considering variable thermo-physical properties, are as follows:

The volumetric rate of entropy generation is evaluated from the following relation [33]:

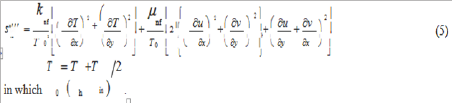
The dimensionless form of the governing equations is obtained using the following dimensionless parameters:

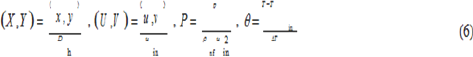
where Dh is the hydraulic diameter of the microchannel and ∆T = T_h - T_in Hence, the non-dimensionalized governing equations alter as follow by using the foregoing dimensionless parameters:

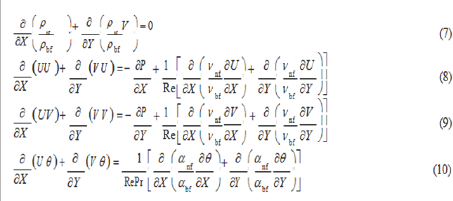
And

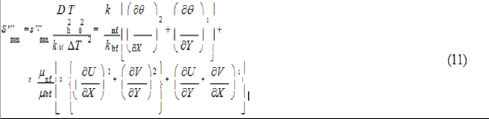
The Reynolds and Prandtl numbers, and irreversibility distribution ratio are defined, respectively, as

Where x is assumed 10-4 in this study [34].

Boundary conditions

Considering the slip velocity and temperature jump on all of the walls, the boundary conditions of the nanofluid flow can be expressed as follows [10]:

where θ w=1 and U w = 0 and n is the normal outward direction. The coefficients of (σv,σT,γ)in most of the engineering applications are equal to one [10]. It should be noted that the other terms in complete forms of Eqs. (14) and (15) are neglected [10]. So, the simplified boundary conditions are:

Thermo-physical properties of the nanofluid

In present study, the thermophysical properties of Al₂O₃- water were determined by the correlations proposed by Khanafer and Vafai [35] as follows:

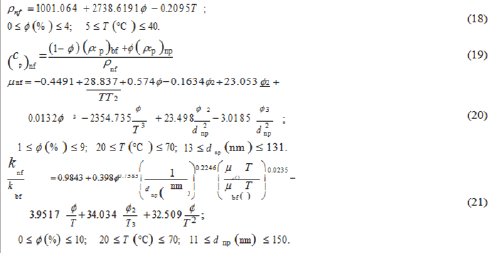
It should be noted thatϕ in dynamic viscosity and thermal conductivity correlations is in percent (%), the dynamic viscosity is in mPa s, dnp stands for nanoparticles diameter in nm, and the temperature is in centigrade (°C) and is limited between the hot wall temperature Th = 40°C and the cold wall temperature Tc = 20°C; hence, the reference temperature is T0 = 30°C. Constant parameters include

which are nanoparticles density, nanoparticles specific heat capacity, base fluid specific heat capacity, base fluid thermal conductivity and Prandtl number, respectively. In addition, correlations (14) and (16) are also valid for the pure fluid when ϕ = 0. The dynamic viscosity (Pa s) of water can be expressed as [35]:

The local Nusselt number is obtained from the following relation:

The average Nusselt number, which is obtained by integrating from Eq. (23) along the hot surfaces, is

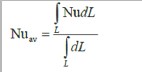
The total entropy generation rate can be expressed as follows:

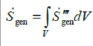
Numerical implementation

The Finite Volume Method (FVM) based on SIMPLER algorithm is employed to solve the governing equations. At first, a finite difference mesh is generated in the solution domain and then, a control volume is created around each node. Subsequently, the governing equations are integrated over each control volume, and by discretizing them, sets of coupled nonlinear differential equations are obtained. The set of discretized equations are solved using a line-by-line TDMA solver. Both of the adjective and diffusive fluxes of each control volume are merged using a power-law differencing scheme.

Grid independence test

In order to find a proper grid which determines that the results are independent from grid, a grid independence test is conducted for the present study at Re = 10, Kn = 0.1 and ϕ =3%. The obtained overall entropy generation rate for different girds is presented in Table 1. As evidenced by this table, 361-131 is the appropriate grid size which guarantees proper numerical modeling.

Verification of the code

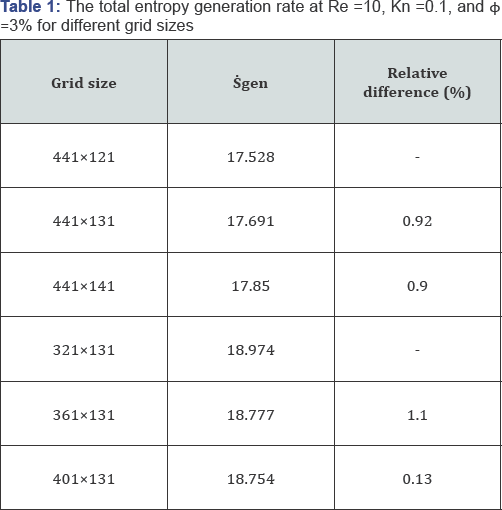
In order to verify the computer program, the results of the study performed by Akbarinia et al. [10] are simulated with our program and their results are compared with ours in (Figure 2). As can be observed from the figure, an excellent conformity exists between our simulation and those of Akbarinia et al. [10] which certify modeling results accuracy

Results and Discussion

In the present study, flow field, heat transfer and entropy generation is scrutinized for forced convection of A12O3- water nanofluid in a parallel plate microchannel with four square impediments. The slip velocity and temperature jump boundary conditions are also considered. In order to obtain the thermophysical properties of Al2O3-water nanofluid Khanafer & Vafai [35] correlations were employed. Moreover, the effect of different parameters such as Reynolds number, Knudsen number, and volume fraction of nanoparticles on the average Nusselt number and total entropy generation rate is evaluated. This study was conducted for Re = 0.1, 3,7 and 10, Kn = 0, 0.035, 0.07 and 0.1, and ϕ = 0, 1, 2 and 3%.

Streamlines and isothermal lines

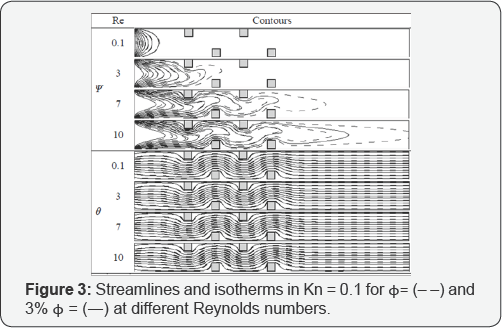
In Fig. 3, streamlines and isothermal lines are depicted in Kn = 0.1, ϕ = 0 and 3%, and in different Reynolds numbers. As can be seen in this (Figure 3), in Re = 0.1, there is a hot region in terms of temperature all over the microchannel as far as the viscosity forces are dominant in this region compared to the inertia forces. Therefore, at the beginning of the microchannel an intense temperature gradient is observed and after that, the temperature becomes constant. Over the top and bottom hot wall the vertical temperature gradient is very low nearly all over the microchannel and as a result, the rate of heat transfer is low. Generally, by increasing the Reynolds number, the temperature gradient over the hot surfaces increases and as a result, the heat transfer rate augments. Moreover, as the Reynolds number increases, over the obstacles, the accumulation of the streamlines increases, and as a result, the velocity of the flow increases significantly in these regions. In Re = 10, the isothermal lines are extended to the end of the microchannel. Furthermore, over the impediments, the isotherms are heaped up due to augmentation of fluid velocity in these zones, and therefore the heat transfer on the spots, and especially over the first two impediments, increases. Moreover, on the hot top and bottom plates, the vertical temperature gradient for nanofluid is less than pure fluid which is due to higher thermal diffusivity of nanofluid (α_βϕ) than pure fluid(α_βϕ) .

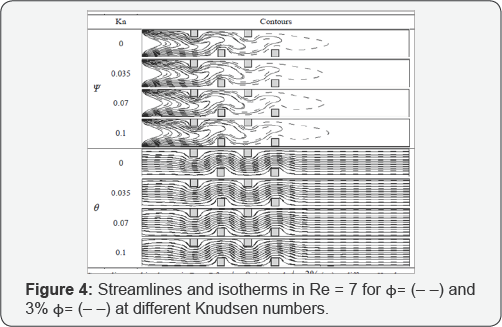
In (Figure 4) streamlines and isothermal lines are depicted in Re = 7, ϕ = 0 and 3%, and in different Knudsen numbers. As can be seen in this figure, the variation of the Knudsen numbers does not have a significant effect on the isotherms. Furthermore, augmentation of the Knudsen number results in approaching the streamlines to the walls and obstacles due to the fact that by considering the slip flow, the flow over the boundaries has velocity and increasing of the Knudsen number, intensifies this phenomenon. What’s more, because the velocity profile is considered to be fully developed, the streamlines are parallel through the microchannel.

The average Nusselt number and total entropy generation rate

Figure 5 indicates variations of the average Nusselt number against the volume fraction of nanoparticles at different Reynolds and Knudsen numbers. According to the figure, by increasing the volume fraction of nanoparticles, the average Nusselt number and heat transfer increase. Furthermore, with augmentation of the Reynolds number, the average Nusselt number increases. What's more, as the Knudsen number increases, the average Nusselt number decreases. (Figure 6) indicates variations of the average Nusselt number against the Knudsen number at different Reynolds numbers and volume fraction of nanoparticles. According to the figure, by increasing the volume fraction of nanoparticles, the average Nusselt number and heat transfer increase. Furthermore, with augmentation of the Reynolds number, the average Nusselt number increases. What's more, as the Knudsen number increases, the average Nusselt number decreases. (Figure 7) indicates variations of the total entropy generation rate against the volume fraction of nanoparticles at different Reynolds and Knudsen numbers. According to the figure, by increasing the volume fraction of nanoparticles or the Reynolds number, the entropy generation rate increases. What's more, when the Knudsen number increases, the total entropy generation rate decreases due to reduction of the temperature and velocity gradients.

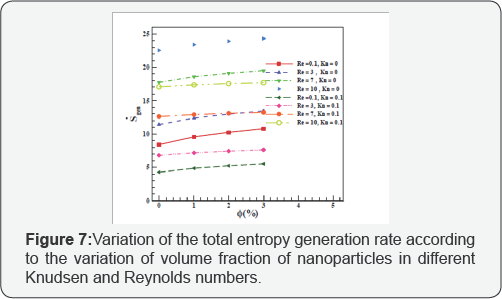
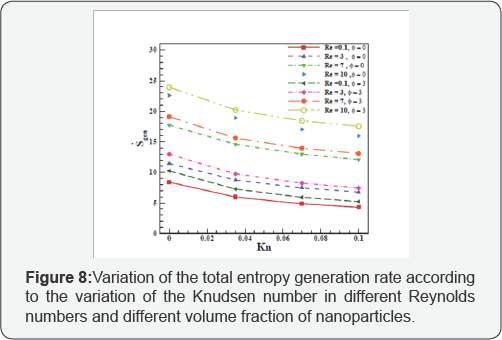
Figure 8 indicates variations of the total entropy generation rate against the Knudsen number at different Reynolds numbers and volume fraction of nanoparticles. According to the figure, as the Knudsen number increases, the total entropy generation rate decreases. Moreover, by increasing the volume fraction of nanoparticles or the Reynolds number, the total entropy generation rate increases.

Conclusion

In this study, flow field, heat transfer and entropy generation are investigated for forced convection of Al2O3-water nanofluid in a microchannel. The properties of nanofluid are considered variable. Moreover, the slip velocity and temperature jump boundary conditions are taken into account in formulating the governing equations. The effects of different parameters such as Reynolds number, volume fraction of nanoparticles, and Knudsen number on the average Nusselt number and the total entropy generation rate are evaluated.

Based on the results

Over the top and bottom hot wall the vertical temperature gradient is very low nearly all over the microchannel and as a result, the rate of heat transfer is low.

By increasing the volume fraction of nanoparticles or the Reynolds number, the average Nusselt number and the total entropy generation augment.

As the Knudsen number increases, both the average Nusselt number and the total entropy generation rate decrease.

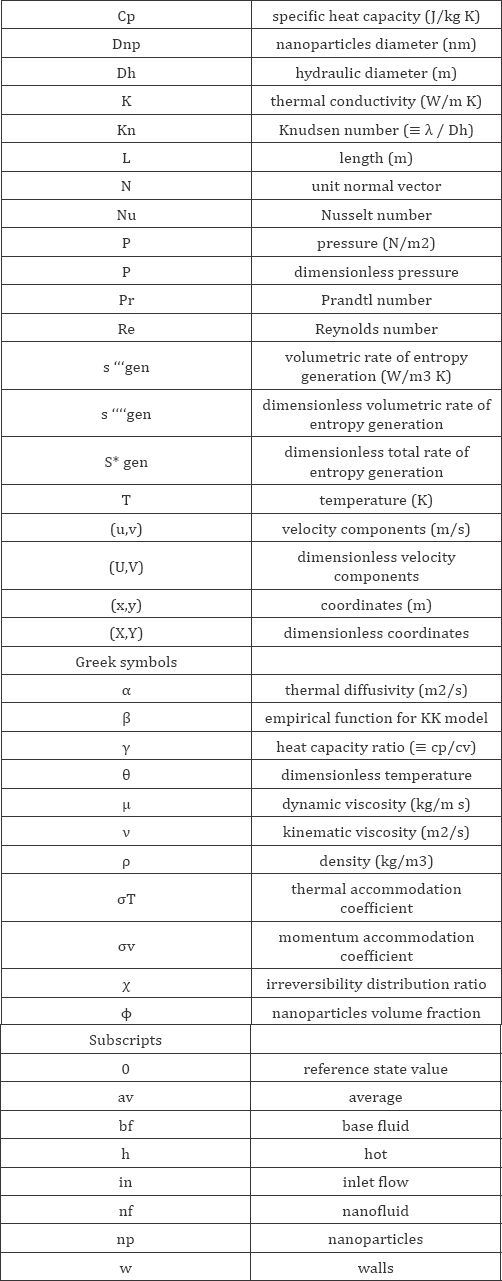
Nomenclature

References

1. Shiping Yu, Timothy A Ameel (2001) Slip-flow heat transfer in rectangular microchannels,” International Journal of Heat and Mass Transfer 44(22): 4225-4234.
2. Barkhordari M, Etemad SG (2007) Numerical study of slip flow heat transfer of non-Newtonian fluids in circular microchannels. International Journal of Heat and Fluid Flow 28(5): 1027-1033.
3. Hamid Niazmanda, Metin Renksizbulutb, Ehsan Saeedi (2008) Developing slip-flow and heat transfer in trapezoidal microchannels. International Journal of Heat and Mass Transfer 51(25-26): 6126-6135.
4. Hooman K, Hooman F, Famouri M (2009) Scaling effects for flow in micro-channels: variable property, viscous heating, velocity slip, and temperature jump. International Communications in Heat and Mass Transfer 36(2): 192-196.
5. Mostafa Shojaeian, Seyed Ahmad Reza Dibaji (2010) Three-dimensional numerical simulation of the slip flow through triangular microchannels. International Communications in Heat and Mass Transfer 37(3): 324-329.
6. Mostafa Shojaeian, Ali Kosar (2016) Convective heat transfer of non-Newtonian power-law slip flows and plug flows with variable thermophysical properties in parallel-plate and circular microchannels. International Journal of Thermal Sciences 100: 155-168.
7. Tuckerman DB, Pease RFW (1981) High-performance heat sinking for VLSI. IEEE Electron device letters 2(5): 126-129.
8. Madhawa Hettiarachchi HD, Mihajlo Golubovic, William M Worek, Minkowycz WJ (2008) Three-dimensional laminar slip-flow and heat transfer in a rectangular microchannel with constant wall temperature. International Journal of Heat and Mass Transfer 51(21-22): 5088-5096.
9. Shams M, Shojaeian M, Aghanajafi C, Dibaji S (2009) Numerical simulation of slip flow through rhombus microchannels. International Communications in Heat and Mass Transfer. 36(10): 1075-1081.
10. Akbarinia A, Abdolzadeh M, Laur R (2011) Critical investigation of heat transfer enhancement using nanofluids in microchannels with slip and non-slip flow regimes. Applied Thermal Engineering 31 (4): 556-565.
11. Arash Karimipour (2015) New correlation for Nusselt number of nanofluid with Ag/Al₂O₃/Cu nanoparticles in a microchannel considering slip velocity and temperature jump by using lattice Boltzmann method. International Journal of Thermal Sciences 91: 146-156.
12. Amin Ebrahimia, Ehsan Roohia, Saeid Kheradmand (2015) Numerical study of liquid flow and heat transfer in rectangular microchannel with longitudinal vortex generators. Applied Thermal Engineering 78: 576583.
13. Abbassi H (2007) Entropy generation analysis in a uniformly heated microchannel heat sink. Energy 32 (10): 1932-1947.
14. Guillermo Ibáñez, Aracely López, Joel Pantoja, Joel Moreira, Juan A Reyes (2013) Optimum slip flow based on the minimization of entropy generation in parallel plate microchannels. Energy 50: 143-149.
15. Mahmoud Abbaszadeh, Ahmad Ababaei, Ali Akbar Abbasian AraniAli, Abbasi Sharifabadi (2016) MHD forced convection and entropy generation of CuO-water nanofluid in a microchannel considering slip velocity and temperature jump. Journal of the Brazilian Society of Mechanical Sciences and Engineering 39(3): 775-790.
16. Ghanbarali Sheikhzadeh, Alireza Aghaei, Hamidreza Ehteram (2016) Analytical study of parameters affecting entropy generation of nanofluid turbulent flow in channel and micro-channel. Thermal Science 20(6): 2037-2050.
17. Hooman K (2007) Entropy generation for microscale forced convection: effects of different thermal boundary conditions, velocity slip, temperature jump, viscous dissipation, and duct geometry. International Communications in Heat and Mass Transfer 34(8): 945-957.
18. Sohel M, Saidur R, Hassan N, Elias M, Khaleduzzaman S, et al. (2013) Analysis of entropy generation using nanofluid flow through the circular microchannel and minichannel heat sink. International Communications in Heat and Mass Transfer 46: 85-91.
19. Pourmahmoud Nader, Soltanipour Hosseinali, Mirzaee Iraj (2015) The effects of longitudinal ribs on entropy generation for laminar forced convection in a microchannel. Thermal Science 20(6): 1963-1972.
20. Hajialigol N, Fattahi A, Ahmadi MH, Qomi ME, Kakoli E (2015) MHD mixed convection and entropy generation in a 3-D microchannel using Al₂O₃-water nanofluid. Journal of the Taiwan Institute of Chemical Engineers 46: 30-42.
21. Rahmati AR, Roknabadi AR, Abbaszadeh M (2016) Numerical simulation of mixed convection heat transfer of nanofluid in a double lid-driven cavity using lattice Boltzmann method. Alexandria Engineering Journal 55(4): 3101-3114.
22. Mahdi Mollamahdi, Mahmoud Abbaszadeh, Ghanbar Ali Sheikhzadeh (2016) Flow field and heat transfer in a channel with a permeable wall filled with Al₂O₃-Cu/water micropolar hybrid nanofluid, effects of chemical reaction and magnetic field. Journal of Heat and Mass Transfer Research (JHMTR).
23. Sheikhzadeh G, Ghasemi H, Abbaszadeh M (2016) Investigation of Natural Convection Boundary Layer Heat and Mass Transfer of MHD water-Al₂O₃ Nanofluid in a Porous Medium Int J Nano Stud Technol 5 (2): 110-122.
24. Arani AAA, Abbaszadeh M, Ardeshiri A (2016) Mixed convection fluid flow and heat transfer and optimal distribution of discrete heat sources location in a cavity filled with nanofluid. Transport Phenomena in Nano and Micro Scales.
25. Aminossadatia SM, Raisib A, Ghasemi B (2011) Effects of magnetic field on nanofluid forced convection in a partially heated microchannel. International Journal of Non-Linear Mechanics 46(10): 1373-1382.
26. Baheri Islamia S, Dastvareha B, Gharraei R (2014) An investigation on the hydrodynamic and heat transfer of nanofluid flow, with non- Newtonian base fluid, in micromixers. International Journal of Heat and Mass Transfer 78: 917-929.
27. Alireza Aghaei, Hossein Khorasanizadeh, Ghanbarali Sheikhzadeh, Mahmoud Abbaszadeh (2016) Numerical study of magnetic field on mixed convection and entropy generation of nanofluid in a trapezoidal enclosure. Journal of Magnetism and Magnetic Materials 403: 133-145.
28. Li Jie (2008) Computational Analysis of Nanofluid Flow in Microchannels with Applications to Micro-heat Sinks and Bio-MEMS: ProQuest pp 1-221.
29. Hsieh CY, Yang AS (2009) Mixing enhancement of a passive micromixer by applying boundary protrusion structures. Advanced Materials Research 74: 77-80.
30. Chung CK, Wu CY, Shih TR, Wu CF, Wu BH (2006) Design and Simulation of a Novel Micro-mixer with Baffles and Side-wall Injection into the Main Channel. 1st IEEE International Conference on Nano/Micro Engineered and Molecular Systems pp. 721-724.
31. Afroz Alam, Kwang Yong Kim (2012) Analysis of mixing in a curved microchannel with rectangular grooves. Chemical Engineering Journal 181: 708-716.
32. Baheri Islamia S, Dastvareha B, Gharraei R (2013) Numerical study of hydrodynamic and heat transfer of nanofluid flow in microchannels containing micromixer. International Communications in Heat and Mass Transfer 43: 146-154.
33. Omid Mahiana, Ali Kianifara, Clement Kleinstreuerb, Moh^d A Al Nimrc, Ioan Pop, et al. (2013) A review of entropy generation in nanofluid flow. International Journal of Heat and Mass Transfer 65: 514-532.
34. Fakher Oueslati, Brahim Ben Beya, Taieb Lili (2013) Double-diffusive natural convection and entropy generation in an enclosure of aspect ratio 4 with partial vertical heating and salting sources. Alexandria Engineering Journal 52(4): 605-625.
35. Khalil Khanafera, Kambiz Vafai (2011) A critical synthesis of thermophysical characteristics of nanofluids. International Journal of Heat and Mass Transfer 54(19-20): 4410-4428.