Research Article

A Review of Mathematical Concepts for Calculation of Cancer Parameters

Saganuwan Alhaji Saganuwan*

Department of Veterinary Physiology, Pharmacology and Biochemistry, College of Veterinary Medicine, University of Agriculture, Nigeria

Submission: November 02, 2018; Published: January 11, 2019

*Corresponding Address: Saganuwan Alhaji Saganuwan, Department of Veterinary Physiology, Pharmacology and Biochemistry, College of Veterinary Medicine, University of Agriculture, P.M.B. 2373, Makurdi, Benue State, Nigeria

How to cite this article: Saganuwan Alhaji Saganuwan. Saganuwan Alhaji Saganuwan. Canc Therapy & Oncol Int J. 2019; 12(5): 555849. DOI:10.19080/CTOIJ.2019.12.555849

Abstract

Various mathematical models such as Gompertzian, logistic, exponential and other immunogenic models were integrated for calculation of various cancer parameters. Pharmacokinetic and pharmacodynamic models likened to other models especially, absorption and elimination are considered similar to proliferation and elimination phase of cancerous cells respectively.

Doubling time (TD) is equal to 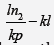whereas reduction time (RT) is 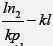and mean proliferation time (MPT) of cancer cells is 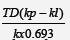. Some revised formulas fit cancer chemotherapy, immunotherapy and chemotherapy/immunotherapy. Some parameters were also calculated to validate the established and newly derived formulas for relevance, construct validity, prediction and reliability. Conclusively, none of the formulas is reliable. However, the formula that considers body surface area may be more relevant to monogastric animals especially dogs and humans. BSA with constant (k), height (0.528) and weight (0.528) functions better for human and dogs. Many other formulas highlighted are also useful.

Keywords: Cancer cell; Gompertzian formula; Chemotherapy; Immunotherapy

Introduction

The first central nervous system (CNS) Anticancer Drug Discovery and Development Conference (ADDDC) was organized and convened out of frustration by dearth of effective anticancer drugs [1]. About 169.3 million years were lost due to cancers in 2008, with colorectal, lung, breast and prostate cancers, respectively [2] having 5-year survival rate as highest for breast cancer, followed by colorectal and prostate cancer, respectively [3] with African countries recording 541,800 deaths [4]. In 2007, over 12-million people were diagnosed with cancer. At least one-third of these individuals are not expected to survive the disease, making cancer the second most prevalent cause of death worldwide. Systemic chemotherapy forms the mainstay of cancer treatment and antimitotics are commonly used to treat a wide variety of cancers [5].

The strategy of chemically targeting cancerous cells at their most vulnerable state during mitosis has instigated numerous studies into the cell death [6], indicating that, there is a high potential for optimization of chemotherapy schedules, although the currently available models are not yet appropriate for transferring the optional therapies into medical practice due to patients, cancer and therapy specific components [7]. Therefore, the development of optional vaccine-chemotherapy protocols for removing tumor cells would be another appropriate strategy in cancer treatment [8]. Since polymorphism can be maintained in a finite population by adaptively turning selection, there is need for a model of resistance in a stochastically evolving cancer cell population [9], with intent to reducing adaptive therapy. However, the growth rate of healthy and tumor cells approach the carrying capacities K1 and K2 respectively [10].

The effect of immune system is to kill the mutated and cancer cells at proportional rates d1 and d2, through apoptosis [11]. The coefficient c represents the portion of the healthy cells, whose genome is disordered by the external esterase. These cells start the neoplastic transformation and are added to the tumor cells [12]. The tumor competes with healthy cells for resources such as blood, nutrients and space [13]. However, an optional control problem for combination of cancer chemotherapy with immune-therapy in form of a boost to the immune system is considered as a multi-input optional control problem [14].

Materials and Methods

Various literatures were searched for mathematical models used in calculation of doubling time of tumor cells, proliferation and loss, tumor volume, immuno-competent cell density, colonization rate and other tumor parameters. Gompertzian, logistic, exponential and other methods were re-viewed for optimization of cancer chemotherapy and immunotherapy [5- 48]. All the formulas derived from various sources are given in equations 1-25. New formulas for calculation of parameters of tumor growth and cytotoxic drugs, cancer immunotherapeutic and cytotoxic/immunotherapeutic were independently and combinedly derived. The reported parameters are given in Table 1. Whereas analysis of doubling times in cancers of selected origin are given in Table 2. However, various parameters are recalculated for some cancer cell types and their cytotoxic drugs are recalculated for construct validity, reliability and prediction of the new formulas.

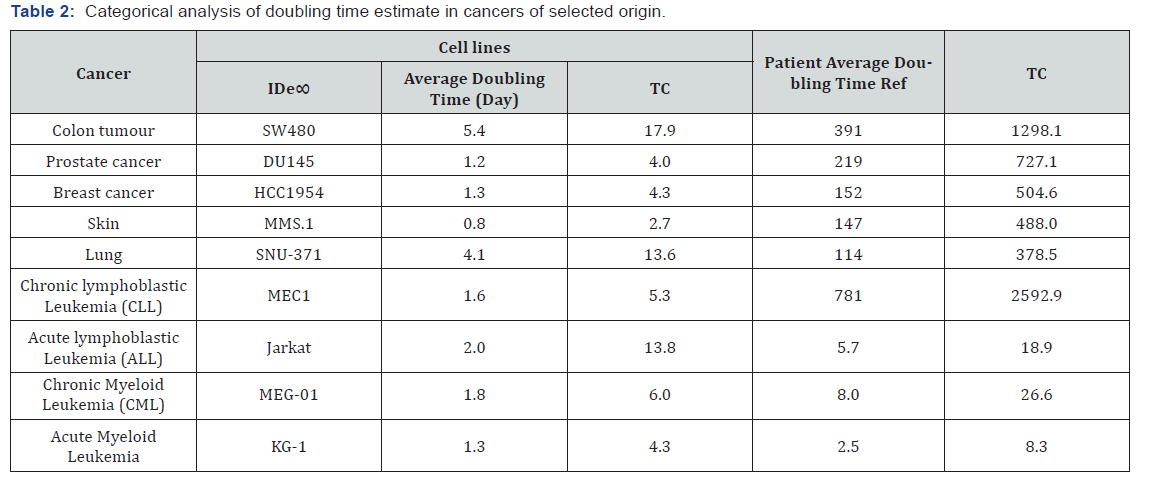
Reference: Chan et al. [6]

Key: TC = Tumor growth delay

Results and Discussion

Cancer cells grow over time. But the rate of growth decreases as the cancer mass increases. Therefore, cell tumor size and tumor volume are proportional

dv/dt= The rate of change in tumor volume per unit time

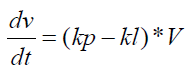
kp = the rate constant for cell production

kl = The rate constant for cell loss

V = Vo exp [(kp – kl)/ (t2 – t1)]

Vo = represents the volume of the tumor at time zero

V = represent the volume of the tumor after the time interval has elapsed (t2 – t1)

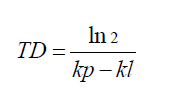
Td = TD = Doubling time of the tumor

Absorption half-life (T½α) = ln2/α

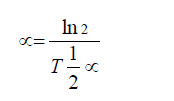
By the time a tumor becomes chemically detectable, it has achieved a mass of approximately lg or 109 tumor cells.

1g of tumor mass = 109 cells = 30 doublings and its growth are no longer exponential. The additional 10 doublings is required to produce 1012 cells or 1kg lesion – a tumor burden at which most patients succumb-occur much more slowly than do the previous 30 doubling and represents a fraction of the tumor’s growth. Tumor growth delay for tumor in vitro and in vivo cell lines are presented in Table 2.

Relationships between Tumor Cell Survival and Drug Dose is Exponential

The number of cells surviving at a given dose of a drug (dN) is proportional to both the drug dose and the number of cells at risk for exposure to the drug (NdD), where N = number of cells in tumor, D = drug dose, dN = - KndD, where proportionality constant – K is introduced with a negative sign. Because the number of cells is expected to decrease with increasing drug dose, the formula is rearranged as follows:

N = No exp – K (D – Do), where the subscript (o) indicates the initial dose and cell number.

Imaging at the beginning of treatment, a tumor contains 10 cells, if each course of treatment results in death of 99.9% of these cells, if no log of cell growth occurs between courses of treatment, five courses of treatment are required to dominate the last cell. The exponential relationship between drug dose and tumor survival dictates that a constant proportion, not number of tumor cells is killed with each treatment cycle. In this example, each cycle of drug administration results in 99.9% (3log) of cell kill, and log of cell growth occurs between cycles.

Assume a tumor contains 1011 cells and the proportionality constant (-K) = -5 for cyclophosphamide (an alkylating agent). If 1.5 of cyclophosphamide is delivered, the tumor will be left with 5.5 x 107 Cells.

N = No exp – K (D – Do); No = 1011 when Do = O

∴N = 1011 exp – 5 (1.5 – O) = 5.5 x 107 cells. If the oncologist chooses to administer 0.75g of cyclophosphamide instead of 1.5g, N = 1011 exp – 5 (0.75 – O) = 2.4 x 109 cells.

The result is that a 50% decrease in dose has translated into a 98% increase in cell survival. Therefore, let liken tumor growth with compartment model of drug disposition in pharmacokinetic. Alkylating agents with antitumor and myelo-suppressive effects are directly proportionate to dose and to the total area under the concentration versus time curve (AUC) rather than to instantaneous plasma drug concentration.

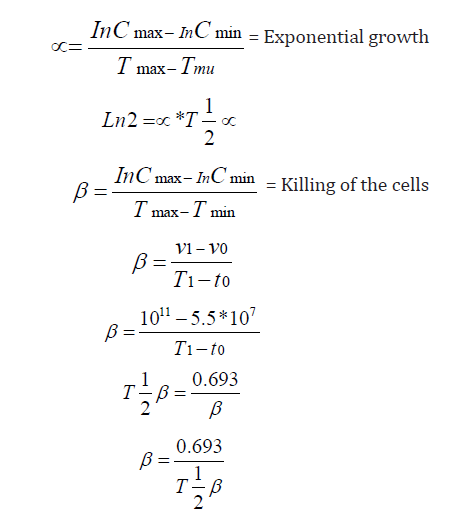
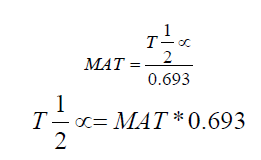
MAT = Mean absorption time

Therefore, substitute for T½ α in equation 1

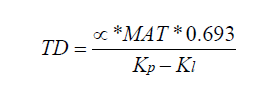
whereas TD is tumor doubling

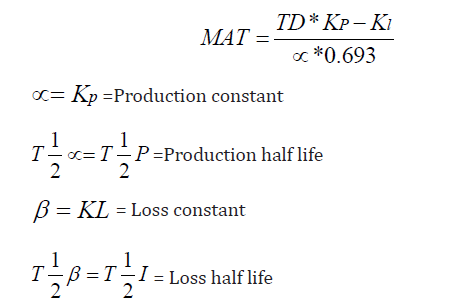
MAT = MPT = Mean production time

Therefore, the derived formulas are presented as follows:

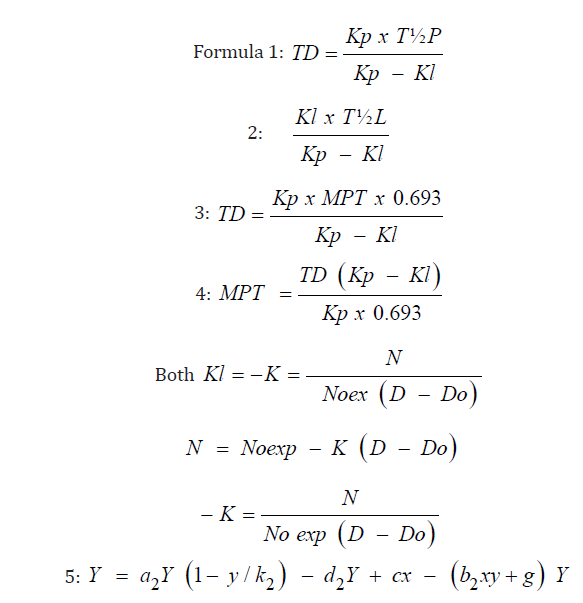
x = healthy cells; y = cancer cells

Their values are non-negative i.e. x ≥ 0; y ≥ 0

The coefficient a, growth rate of healthy cells, a1 = growth rate of cancer cells

K1 = carrying capacity of healthy cells, K2 = carrying capacity of tumor cells, immune system should kill mutated cells at (d1) and cancers cells at (d2)

The tumor competes with healthy cells for resources; blood, nutrients and space. The competition coefficients are b1, b2, and g.

6: The effect of anticancer chemotherapy:

dm/dt = μm +Vm (t)

1.2m/0.8+m for chemotherapy fraction cells kill.

Optional vaccine-chemotherapy protocols for removing tumor cells maybe an appropriate strategy in cancer chemotherapy. A proper treatment method would reduce the population of cancer cells and changes the dynamics of cancer [8].

7: N = ns + nr (N = Inner tumor composition; ns = drug sensitive cells; nr = drug resistant cells)

The capacity to involve and adapt makes successful treatment of cancer difficult. Therefore, high-resolution monitoring of the target population is important [9].

8: Y = μ1 (x − β x2 ) α − dδ y + x + ky yv

An optional control problem for combination of cancer chemotherapy with immunotherapy in form of a boost to immune system is considered as a multi-input optional control problem. Simplified mathematical model may be useful to give some guidance [14]. The exponent 0.67 is needed since anticancer has to be released through the surface of the tumor [15] but 0.528 correlates very well with both human and dogs [16]. However, various body surface area formulas have various exponents which can grossly affect the results [17].

9: I (Inhibitor) = dp 2/3 q

Resistance factor should be responsible for the effect of drug resistance of tumor cells on the dynamical growth for the tumor. Optional control problems have common point wise both different integral constraints on the control. Bang-bang control is optional if the resistance is sufficiently strong [18].

10: Mt = – M (L) +V (t)

The drug level function m=m(t) obeys linear differential equation with a positive drug decay rate where v(t) denotes the drug dose administered per unit time. The fate of anticancer drugs from introduction into the body to intracellular targets can be represented by pharmacokinetic (pk) compartmental ordinary differential equations (ODEs) for their concentration. This fate is theoretically representable by partial differential equations (PDFs) with boundary conditions instead of exchange rule. But in cell medium, pharmaceutical differential equation must be used to relate local drug concentration with molecular effects on their targets, delte Billy et al. and , also [39].

The most common models of tumor growth are the exponential model DN/DTand the logistics(DN/dt=λ N,(1-N/K), Where K is the maximum tumor size, or carrying capacity of the environment and the Gomperz (DN/dt=λ Nln(K/N))where again K is the carrying capacity. Contrary to the exponential and logistic models the Gompertz model was initially developed in the context of insurance [19] and was just used in the nineties to fit exponential data of tumor growth [20]. Murray [21] considered two – population Gompertz growth model with a loss term to model the effect of cytotoxic drug.

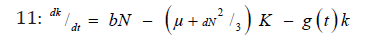
Where b is the rate of tumor-induced vascular formation, K + dN2/3 represents the rate of spontaneous and tumor-induced vascular loss, g (t) ≥, 0 represents the antiangiogenic drug concentration

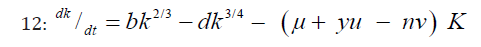
μ = dose of antiangiogenic drug; V = dose of cytotoxic drugs; Q1Y1, n = their effects in tumor cells and on vasculature.

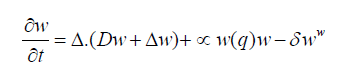
Where m denotes the density of endothelial cells; Dm= diffusion rate; αm = proliferation rate; Xm = chemotaxis rate; δm = death rate; w = the concentration of chemoattractant substance; Dw = diffusion rate; δw = production rate that depends on the density of quiescent tumor cells q; δw = degradation rate.

A mathematic model for time used to theoretically investigate anticancer therapy such as surgery and chemical treatments has been established. Theoretically optional schedules are derived which show superiority of a metronomic administration sequence on a classical maximum tolerated dose scheme for the total metastatic burden in the organ, [38].

Tumors have two phenotypical traits: volume denoted by V, also to as size expressed in mm3 and caring capacity denoted by K, expressed also in mm3. Hence, physiological domain where metastases live is the square Ω = [Vo −V max]*[Vo,V max] whose boundary is devoted by ∂Ω with external normal vector V(δ).

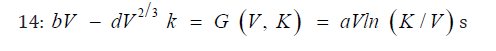
a = parameter controlling the cancer cells proliferation kinetics

a = parameter controlling the cancer cells proliferation kinetics

d = Parameter for production and effect of angiogenesis inhibitors

The main assumption underlying the model is that, clearance rate of inhibitors (e.g. endostatin, angiostatin, thrombospondin

1) is much smaller than clearance stimulators (e.g. vascular endothelial growth factor based on fibroblast growth factor. The concentration of inhibitors should be proportional to the surface of the tumor giving rise to 0.67 power in the inhibition term. The number of metastases emitted by a tumor with volume V for unit of time is given by

15: Β (V) = mVα where α = 0.67 or fully penetrating. The tumor (α = 1) and 0.75 or even having any fractal dimension between 2 and 3 or 4.

16:A(t)=DNI-1exp(-Ur(t-ti)lt≥ti where D is the administered dose ti’s are the administration times and is a Heaviside function having value 1 if and only it t ≥ tj .

A total amount (Amax) has to be given at a constant rate during administration time (t), followed by a rest period from (t) to an arbitrary end time (t).

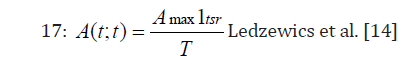
Condition of Maximum Tolerated Dose (MTD) Administration Scheme

Modeling and prediction of the effect of chemotherapy was developed using fractional diffusion equation. The methodology is useful for analysis of the effect of special drug and cancer [22]. Also, a mathematical model for the scheduling of angiogenic inhibitor in combination with a killing agent was considered as an optional control problem, [14]. The initial condition well posed for the optional control problem is not difficult to determine, because the first order necessary conditions for optimality of the controls U and V given by pontryagin maximum principle states that there exists a constant (λo≥O) and an absolutely continued co-vector λ satisfying the equation transversally. Cancer cells can be eradicated in a very short time with a small amount of drug using an optional administration therapy [23]. The best way of reducing the tumor burden after a fixed period of treatment is to keep the tumor size to minimum initially and then fire high intensity treatment towards the end of the treatment period [24]. But stochastic model provides a description of the optimal therapeutic regimen [25] Endothelial birth (b) and death(d) rate depend mainly on the type of tumor and the patient tumor cannot increase over the maximum volume: C∞ = e∞ = (b/d)³/² nd then does not consider evolution to metastasis [26].

18: However, tumor width (mg) =a*b²/2

a & b, the tumor length and weight in mg must be considered in the calculation of cancer parameters.

T - C; T is the median time (days) required for tumors to reach a predetermined size (e.g. 1000mg), and C is the median time (days) for the control tumors to reach the same size.

19: Tumor Cell kill = Log10 cell kill total (gross) =T-C/3.32*Td

T - C is the tumor growth delay; Td = the tumor volume doubling time (days) estimated from the best fit straight line from linear growth plot of the control tumors in exponential growth (100 – 800 range). The conversion of the T-C values to log10 cell kill is possible, because the Td of tumors re-growing post treatment (Rx) approximates the Td values of the tumors in untreated control mice. The calculations for net log10 tumor cell kill is provided by subtraction of the duration of the treatment period from the T-C value and then divide by 3.32 x Td

Many solid tumors have shown empirically [27] to follow the Gompertz growth law [28].

20: Therefore,V=V0exp[k0/∝(1-e^-αt)]

Where V = Volumetric size of the tumor of time, t and V0, K0, and α are constants

21: But growth equation with growth constant

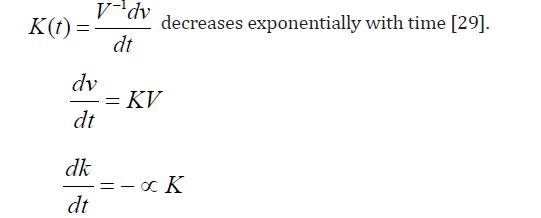
With V(o) = Vo, K(o) = Ko, show that an equivalent result is obtained by the assumption [28]

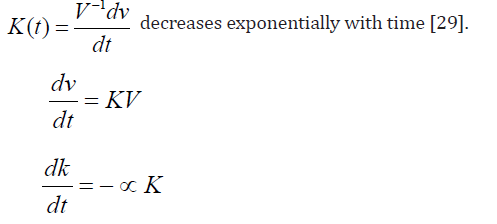
22: Since all mitotic phases express ki – 67 antigens,

But tumors with less than 250 MIB-1 positive cells are excluded [30].

23: Cell cycle time and potential doubling time are calculated for meningiomas and neurinomas as follows:

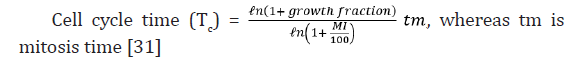
24: However, tumor potential can also be calculated as follows:

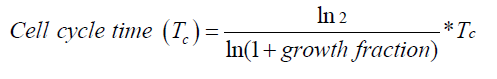
whereas Tpot is the tumor potential,[40]

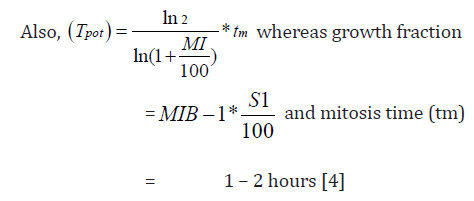
25: Tumor doubling time (Td) can also be calculated as follows:

volume after t days [47]

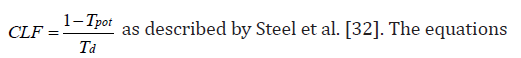
(22 – 26) are very useful for calculation of cancer parameters for meningiomas and neurinomas [33].

However, tumor inhibition rate % = (Mean tumor weight of control group – Mean tumor weight of treated group) over mean tumor weight of control group x 100 can be applied for hepatocellular carcinoma H22 cell line in mice [34]. The time it takes for a tumor mass to double is known as the doubling time which varies according to the size of tumor, but for most solid tumors, it is about 2-3 months (60-90 days). Initially the growth is exponential and then slows as the tumor increases in size and age called Gompertzian growth. Generally, chemotherapy is most successful when the number of tumor cells is low and the growth fraction is high, which is the situation in the very early stages of cancer. The larger the tumor mass, the more likely it has metastasized to other sites [35]. Cancer chemotherapy is goalspecific. For the patient to be cancer-free, the treatment must be total. But if the treatment is palliative, the quality of life may be improved, and higher heart rate variability does not only predict lower tumor burden but also improves survival in humans [36].

Conclusion

Therefore, cell kill hypothesis is a theoretical model that predicts the ability of antineoplastic drugs to eliminate cancer cells. A 1-cm breast tumor may already contain 109 cancer cells before it can be detected during manual examination. After first round of chemotherapy the cancer cells is reduced to 107(99% kill). When second round of chemotherapy is applied the cancer cells reduce to 106. At this point, T cells are removed remaining cancer cells. It is likely that no antineoplastic drug or combination of drugs will kill 100% of tumor cells. A relatively small number of cancer cells may be removed after chemotherapy suggesting that early diagnosis and treatment may be the goal standard [37]. But the reviewed formulas can be used to determine cancer parameters whose values may indicate whether one or more of therapeutic interventions can be successful [38-48].

References

1. Levin VA, Tonge PJ, Gallo JM, Birtwistle MR, Dar AC, et al. (2015) CNS anticancer drug discovery and development conference white paper. Neuro Oncol Suppl 6: vi1-26.
2. Soerjomataram L, Lortet Tieulent J, Parkin DM, Ferlay J, Mathers C, et al. (2012) Global burden of cancer in 2008: a systematic analysis of disability-adjusted life-years in 12 world regions. Lancet 380: 1840- 1850.
3. Coleman MP, Quaresma N, Berrino E, Lutz JM, Angelis RD, et al. (2008) Cancer survival in five continents: a worldwide population-based study. Lancet Oncol 9: 730-756.
4. Ferlay J, Shin HR, Bray E, Forman D, Mathers C, et al. (2010) Estimates of worldwide burden of cancer in 2008. Int J Cancer 127: 2893-2917.
5. Gascoigne KE, Taylor SS (2009) How do anti-mitotic drugs kill cancer cells. J Cell Sci 122: 2579-2555.
6. Chan KS, Koh CG, Li HT (2012) Mitosis-targeted anticancer therapies where they stand. Cell Death Dis. 3:e411.
7. Engelhart M, Lebiedz D, Sager S (2011) Optimal control for selected cancer chemotherapy ODE models: a review on the potential of optimal schedules and choice of objective function. Math Biosci 229(1): 123- 134.
8. Ghaffari A, Nazari M, Arab F (2014) Optimal finite cancer treatment duration by using mixed vaccine therapy and chemotherapy: state dependent Riccati equation control. Journal of Applied Mathematics ID: 363109: 1-9.
9. Fischer A, Vazquez Garacia IN, Mustonnan V (2015) The value of monitoring to control evolving populations. PNAS 112(4): 1007-1012.
10. Sachs RK, Hlatky LR, Hanfeldt P (2001) Simple ODEs model of tumor growth and anti-angiogenic or radiation treatment. Mathematical and Computer Modeling 33(12-13): 1297-1305.
11. Wei X, Guo C (2010) Global existence for a mathematical model of the immune response to cancer. Nonlinear Analysis: Real world Applications 2(5): 3903-3911.
12. Hirata Y, Bruchovsky N, Aihara K (2000) Development of a mathematical model that predicts the outcome of hormone therapy for prostate cancer. J Theor Biol 264(2): 517-527
13. Kuang T, Nagay TD, Elser JJ (2004) Biological stoichiometry of tumor dynamics: mathematical models and analysis. Discrete and Continuous Dynamical Systems B 4(1): 221-270.
14. Ledzewics U, Musalman MSF (2013) Optimal controls for a mathematical model of tumor-immune interactions under targeted chemotherapy with immune boost. Discrete and Continuous Dynamical Systems Series B18(4): 1031-1051.
15. Ledzewics U, Schattler H (2006) Anti-angiogenic therapy in cancer treatment as an optimal control problem. National Science Foundation, SIUE, Summe Research Fellowship pp. 1-28.
16. Saganuwan SA (2017) Derivation of a unique body surface area (bsa) formula for calculation of relatively safe doses of dog and human anticancer drugs. Journal of Cancer Science and Therapy 9(10): 690- 704.
17. Saganuwan SA, Ndakotsu AM (2015) Standardization and scoring of the body surface area (BSA) formulas for calculation of the doses of anticancer agents for cancer patients from the Northwestern Nigeria. Journal of Cancer Science and Therapy 7(1): 12-18.
18. Krabs W, Von Woldferbdort L (2011) Two optimal control problems in cancer chemotherapy with drug resistance. Annals of the Academics, of Romanian Scientist Series on Mathematics and its Applications 3(2): 332-354.
19. Gompertz B (1825) On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingences. Philos. Transact. of the Royal Society of London 115: 513-585.
20. Laird A (1964) Dynamics of tumor growth. Br J Cancer 13: 490-502.
21. Murray J (1990) Optimal scheduling of two dongs with simple resistance for problem in cancer chemotherapy IMA. Journal of Mathematics, Applied Medicine and Biology 100: 49-67.
22. Namazi H, Kulish VV, Wong A (2015) Mathematical modelling and prediction of the effect of chemotherapy on cancer cells. Scientific Reports 5: 13583.
23. Itik M, Dakmici MU, Bank SP (2009) Optimal control of drug therapy in cancer treatment. Nonlinear Analysis: Theory, Methods and Application 71 (12): 1473-e1486.
24. Martin RB (1992) Optimal control drug scheduling of cancer chemotherapy. Automatica 28(6): 1113-1123.
25. Codman AJ, Murray JM (2000) Optimal control for a stochastic model of cancer chemotherapy. Mathematical Bioscience 168(2): 187-200.
26. Mellal L, Folio D, Belharet K, Ferreira A (2016) Modeling of optimal targeted therapies using drug-loaded magnetic nanoparticles for the liver cancer. IEEEE Transactions on Nano Bioscience, Institute of Electrical Electronics Engineering: 10-99.
27. Laird AK (1965) Dynamics of Tumor Growth: Comparison of Growth Rates. British Journal of Cancer 19: 278.
28. Rubinow SI (2002) Introduction to Mathematical Biology, Dover Publications, Inc., New York, USA, p. 386.
29. Laird AK, Tyler SA, Barton AD (1965) Dynamics of normal growth. Growth 29: 233.
30. Santisteaban MS, Brugal G (1994) Image analysis of in situ cell cycle related changes of PCNA and ki_67 proliferating antigen expression. Cell proliferation 27: 435-453.
31. Bruno S, Darzynkiewicz Z (1992) Cell cycle dependent expression and stability of the nuclear protein detected by ki-67 antibody in HL-60 cells. Cell prolif 25: 31-40.
32. Steel GG (1968) Cell loss from experimental tumors. Cell Tissue Kinetics 1: 193-207.
33. Nakasu S, Nakasu Y, Sakajima M, Yokoyama M, Matsuda M, et al. (1996) Potential doubling time in meningiomas and neurinomas. Acta Neurochir 138: 763-770.
34. Lai X, Xia W, Wei J, Ding X (2017) Therapeutic effect of Astragalus polysaccharides on hepatocellular carcinoma H22-bearing mice. Dose- Response 1-6.
35. Walker R, Whittlesea C (2012) Clinical Pharmacy and Therapeutics. 5th (edn), Churchill Livingstone Elsevier pp. 983.
36. Pecceu E, Stebbling B, Pereira YM, Handel I, Culshaw G, et al. (2017) Vasovagal tonus index (VVTI) as an indirect assessment of remission status in canine multicentric lymphoma undergoing multi-drug chemotherapy. Veterinary Research Communication 41: 249-256.
37. Adams MP, Koch RW (2010) Pharmacology Connections to Nursing Practice, Pearson, New Jersey, USA, pp. 1526.
38. Benzekry B, Barbolosi D, Benabdallah A, Habert F, Hahnteldt P (2010) Quantitative analysis of the tumor metastases system and its optimal therapeutic control. Cornell University Library.
39. Billy F, Clairambault J, Fercoz O (2016) Optimization of cancer drug treatment using population dynamics. Hal Archives.
40. Burger PC, Shibata T, Kleihues P (1989) The use of monoclonal antibody ki-67 in the identification of proliferating cells: application to surgical neuropathology. Am J Surg Pathol 10: 611-617.
41. Gompertz B (1825) On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingences. Philos Transact. of the Royal Society of London 115: 513-585.
42. Hahnfeldt P, Panigraphy D, Folkman J, Hlatky L (1999) Tumor development under angiogenic signaling; a dynamical theory of tumor growth, treatment, response and postvascular dormancy. Cancer Res 59(19): 4770-4775.
43. Kusnetsov VA, Makalkin IA, Taylor MA, Perelson AS (1994) Nonlinear dynamics of immunogenic tumors. Parameter estimation and global bifurcation analysis. Bulletin of Mathematical Biology 56: 295-321.
44. Lenhard RE, Osteen RT, Gansler T (2001) The American Cancer Society Clinical Oncology. Blackwell Science Inc., Malden, USA pp. 919.
45. Meyer JS (1981) Growth and cell kinetic measurements in human tumors. Pathol Annu 16: 53-80.
46. Stepanova NV (1980) Course of the immune reaction during the development of a malignant tumor. Biophysics 24: 917-923.
47. Teicher BA (2016) Anticancer Development Guides Pre-clinical screening, Clinical Trials and Approval, Springer Sciences and Business Media, pp. 311
48. Yoshii Y, Maki Y, Tsuboi K, Tomono Y, Nakagawa K, et al. (1986) Estimation of growth fraction with bromodeoxyuridine in human central nervous system tumors. J Neurosurg 65: 659-663.