Cancer Therapy and Oncology International Journal (CTOIJ)

Review Article

Towards a Universal Law Controlling all Human Cancer Chromosome LOH Deletions, Perspectives in Prostate and Breast Cancers screening

Jean-Claude Perez*

Retired interdisciplinary researcher (IBM), France

Submission: October 23, 2017; Published: January 09, 2018

*Corresponding author: Jean-Claude Perez, Retired interdisciplinary researcher (IBM), £ 7 avenue de terre-rouge F33127 Martignas Bordeaux metropole France, Email: jeanclaudeperez2@gmail.com

How to cite this article: Jean-Claude Perez. Towards a Universal Law Controlling all Human Cancer Chromosome LOH Deletions, Perspectives in Prostate and Breast Cancers screening. Canc Therapy & Oncol Int J. 2018; 9(2): 555756.DOI:10.19080/CTOIJ.2018.09.555756

Abstract

Background: Global analysis of 3 human genomes of increasing levels of evolution (Neanderthal /Sapiens Build34/Sapiens hg38) reveals 2 levels of numerical constraints controlling, structuring and optimizing these genome’s DNA sequences. A global constraint - called "HGO” for "Human Genome Optimum” - optimizes the genome at its global scale. The same operator applied to each of the 24 individual chromosomes reveals a hierarchical structure of these 24 chromosomes.

Methods: We analyze how this HGO genomic optimum is perturbed by hundred single or multiple LOH (Loss of Heterozygosity) deletions relating to different chromosomes and cancers.

Results: The generic law highlighted is stated as: "When an LOH deletion affects a chromosome upstream of the HGO point (chromosomes 4 13...) in the chromosomal spectrum, this deletion degrades the genomic optimum of the cancer genome. When an LOH deletion affects a chromosome downstream of the HGO point (chromosomes 19 22...) In the chromosomal spectrum, this deletion improves the genomic optimum of the cancer genome. The exhaustive analysis of the 240 LOHs for the following 6 cases: Chromosome 13 (breast cancer), chromosome 5 (breast cancer), chromosome 10 (glioblastoma cancer), chromosome 1 (colorectal cancer), chromosome 1 (neuroblastoma cancer) and chromosome 16 (prostate cancer) obey this law in 227 cases and do not obey this law for 13 cases (success rate of our law = 94.58%). In this article we will detail this type of analysis on 153 LOH relating to breast and prostate tumors affecting respectively chromosome 13, chromosome 5 (breast) and chromosome 16 (prostate). In this detailed study, the HGO law described here is verified in 143 cases out of 153, or 93.46% of favorable cases.

Conclusion: The main application of this fundamental discovery will be the genomic characterization and classification of tumors, making it possible to predict the dangerousness and even the pathogenicity.

Keywords: Human genome; Cancer; Loss of Heterozygosity; Biomathematics; Evolution

Introduction

The demonstration of an” Human Genome Optimum” through the comparative analysis of genomes to varying degrees of evolution and the study of the hierarchical structure of the 24 individual chromosomes is of great importance. It has led you to a new classification of tumors to prioritize their pathogenicity, which is also remarkable.”

Professor Francois Gros Pasteur Institute Paris (co-discoverer of messenger RNA with James Watson and Walter Gilbert). Thanks to the CRISPR (Clustered regularly interspaced short palindromic repeats) technology, it is now possible to locally modify the genomes, and particularly the human genome [1]. Almost simultaneously, the fractal and global structures of the human genome were demonstrated [2]. In such a context, apart from ethical questions, can a local technology as powerful as CRISPR be applied, ignoring its possible effect on the possible global and long- range equilibria and balancing at the chromosome scale or even the entire genome scale? For more than 25 years, we have been looking for possible global, even numerical, structures that would organize DNA, genes, chromosomes and even whole genomes [3-6]. Curiously, the method of numerical analysis of whole genomes as well as the discovery of a global law of impact of the LOH deletions associated with tumors that will be the subject of this article may seem to the reader too simple or even "naive”... In effect, these laws are based on a well-known type of analysis that could be thought to have explored all aspects: the analysis of GC / TA ratios. It has long been known that such ratios [7].

Characterize the diversity of chromosomes. Under the name of "isochores,” Giorgio Bernardi has extensively explored its richness and diversity [8,9]. We have already demonstrated a numerical structure at the scale of each human chromosome as well as on the whole genome [10-13]. In [10] we have already highlighted this numerical value of 0.6909830056, the HGO in this article: it controls the population of triplets' codons analysing single stranded DNA sequence from the whole human genome. However, it is only by deepening the notion of "fractal periodicity”, outlined in [14], and we will highlight in various articles in preparation [15] that we have re-discovered the major role that this GC / TA ratio at the whole chromosome and whole genome scales. Particularly, in 2015, we have demonstrated [14] how a global structure organizes any DNA sequence. This numerical organization is based on the atomic masses of the "G” bases of the double stranded DNA sequence, therefore on the bases C and G of the single stranded DNA sequence. Here is another reason sufficient to consider the relations and proportions between bases C + G on the one hand, and T + A on the other hand. Comparing the three genomes of reference of Neanderthal [15,16], Sapiens Build34 of 2003 [17] and Sapiens hg38 of 2013 [18], we will demonstrate in the evidence of "Fractals periods "and "resonance periods” characterizing each of the 24 human chromosomes. It is for these simple reasons that we have decided to focus on these C + G / T + A ratios at the scale of each of the 24 human chromosomes as well as on the whole genome analyzing the 46 chromosomes single stranded DNA sequences.

Materials and Methods

Analysed whole human Genomes

We analyzed completely and systematically each of the 24 chromosomes of each of the following three reference genomes:

a) Neanderthal genome

Neanderthal genome (2014) [16]

b) Sapiens Build34 (2003) human reference genome [17]

Sapiens Build34 (2003) genome

c) Sapiens HG38 (2013) human reference genome [18]

Sapiens HG38 (2013) genome

Computing the HGOs

Let us now distinguish the three types of HGO that will be discussed:

A. Theoretical HGO (tHGO) tHGO = (3-PHI>2 =0.6909830056, where PHI is the Golden Ratio PHI =1.618033989

B. Reference woman HGO (rwHGO): rwHGO =0.6913477936

error (tHGO - rwHGO) = 0.6909830056 - 0.6913477936 = "0.0003647879784 and

Reference man HGO (rmHGO) : rmHGO = 0.6922864236

error (tHGO - rmHGO) = 0.6909830056 - 0.6922864236 = "0.001303417973

C. HGO (LOH) is considered as a function: with LOH the deletion disturbing the computed CG/TA whole human genomic ratio and « n » the LOH partially deleted chromosome and « chrs » all chromosomes from 1 to 22 which are different with « n ». HGO is computed by compiling C+G and T+A nucleotides populations from each 46 chromosomes DNA single strand.

Example: HGOwoman (LOH chr n) = (C+G population from 46 chromosomes strand1) + (C+G population from 46 chromosomes strand1)] [ (T+A population from 46 chromosomes strand1) + (T+A population from 46 chromosomes strand1) ] Then:

HGOwoman (LOH chr n) = [ (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chrn) + (sum C+G chrX) + (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chr LOH n) + (sum C+G chrX) ] [ (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chrn) + (sum T+A chrX) (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chr LOH n) + (sum T+A chrX) ] HGOman (LOH chr n) = [ (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chrn) + (sum C+G chrX) + (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chr LOH n) + (sum C+G chrY) ] [ (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chrn) + (sum T+A chrX) (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chr LOH n) + (sum T+A chrY) ]

Recall the single stranded C+G, T+A and individual chromosome HGO values (Table 1). Example of LOH effect on the HGO, the case of a single LOH deletion in chromosome 13 breast tumor (Table 2).

Example of LOH effect on the HGO, the case of a single LOH deletion in chromosome 13 breast tumor:

Computing Detailed Steps

First, the case of a whole woman XX genome:

HGOwoman (LOH chr n) = [ (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chrn) + (sum C+G chrX) + (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chr LOH n) + (sum C+G chrX) ] [ (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chrn) + (sum T+A chrX) (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chr LOH n) + (sum T+A chrX) ] (sum C+G single strand 1 to 22 chromosomes except chr13) CG1TO22 : 96166571 96769083 78577742 72568001 71611274 67360020 64696843 58133960 50270473 55359481 55885058 54275482 0 36982791 35578844 36472718 37575444 31856106 28015712 28010605 16411625 18406838 cumulating CUMCG : 1090984671 (sum T+A single strand 1 to 22 chromosomes except chr13) : TA1TO22 : 134314441 143779145 119522393 117184666 109654104 102718502 94273288 86634176 71520077 77903481 78648684 78862334 0 53585358 49062481 45333225 45344760 48233499 30425046 35933652 23676994 20752939 cumulating CUMTA: 567363245.

(sum C+G chr13) : CGR13 : 37772797

(sum T+A chr13) : TAR13 ; 60210328

(sum C+G chrX) : CGX:61221521

(sum C+G chrY) : CGY : 10572683

(sum T+A chrX) : TAX : 93671508

(sum T+A chrY) : TAY : 15842360

(sum C+G chr 13 LOH ) : CGLOH : 37498415

(sum T+A chr 13 LOH ) : TALOH: 59791746

computing the HGO LOH ratio: HGOWLOH = ( ( CUMCG + CGR13 + CGX ) + ( CUMCG + CGLOH + CGX ) ) + ( ( CUMTA + TAR13 + TAX ) + ( CUMTA + TALOH + TAX ) )

HGOWLOH: 0.6913521525

Detailed intermediary steps:

HGOWLOH: 0.6913521525

( CUMCG + CGR13 + CGX ) : 1189978989

( CUMCG + CGLOH + CGX ) : 1189704607

( CUMCG + CGR13 + CGX ) + ( CUMCG + CGLOH + CGX ) : 2379683596

( CUMTA + TAR13 + TAX ) : 1721245081

( CUMTA + TALOH + TAX ) : 1720826499

( CUMTA + TAR13 + TAX ) + ( CUMTA + TALOH + TAX ) : 3442071580

Now the same summarized computing in the case of a XY man whole genome: HGOman (LOH chr n) =

[ (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chrn) + (sum C+G chrX) + (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chr LOH n) + (sum C+G chrY) ] [ (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chrn) + (sum T+A chrX) (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chr LOH n) + (sum T+A chrY) ] HGOMLOH = ( ( CUMCG + CGR13 + CGX ) + ( CUMCG + CGLOH + CGY ) ) + ( ( CUMTA+ TAR13 + TAX ) + ( CUMTA + TALOH + TAY ) ) HGOMLOH: 0.6922910002 CUMCG + CGR13 + CGX ) : 1189978989 CUMCG + CGLOH + CGY ) : 1139055769 ( CUMCG + CGR13 + CGX ) + ( CUMCG + CGLOH + CGY ) : 2329034758 CUMTA + TAR13 + TAX ) : 1721245081 CUMTA + TALOH + TAY ) : 1642997351 CUMTA + TAR13 + TAX ) + ( CUMTA + TALOH + TAY ) : 3364242432

Computing Errors i.e. Distances

LOH XX genome: 0.6913521525 ^-0.0003691469064

Recall reference XX genome: 0 . 6 9 1 3 4 7 7 9 3 6 ^-0.0003647879784

Error: abs (^-0.0003691469064) > abs(^-0.0003647879784)

Then decreasing woman HGO for this LOH in chromosome13 located upstream to the swapping HGO point. LOH XY genome:0. 6922910002 ^-0.001307994526.

Recall reference XY genome: 0 . 6 9 2 2 8 6 4 2 3 6 ^-0.001303417973

Error: abs (^-0.001307994526) > abs (^-0.001303417973)

Then decreasing man HGO for this LOH in chromosome13 located upstream to the swapping HGO point.

Results

In all that follows, the general methodology will be as follows: we calculate, for the 46 chromosomes constituting each genome studied, only the single-stranded DNA sequences. In these sequences, we count the relative populations of bases T + A on the one hand, and C + G on the other hand.

HGO of the 3 whole genomes: Neanderthal, Sapiens Build34 and Sapiens HG38

The three genomes we compare here are differentiated on the one hand by their respective evolution levels, on the other hand by the sample of individual genomes of which they form the syntheses, and finally by the precision of the sequencing of DNA. For example, this work by the Craig Venter team demonstrates this level of dispersion between more than 10,000 individual genomes and reference genomes such as HG28 [19].

The 3 analysed genomes are:

i. Neanderthal genome (2014) [16]

ii. Sapiens Build34 (2003) genome [17]

iii. Sapiens hg38 (2013) genome [18]

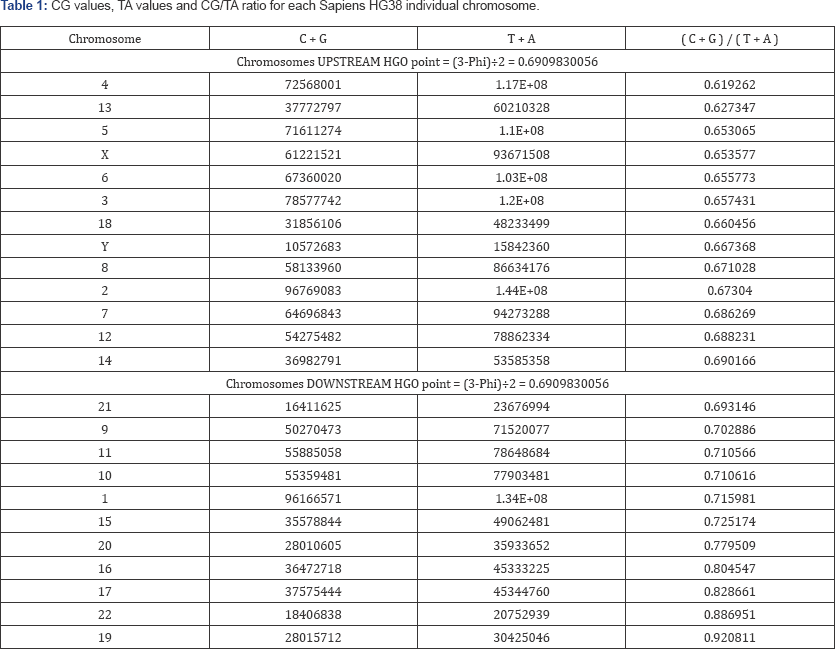
The methods of computing the different HGOs are given in "supporting information part 1". The detailed information on the calculation of the respective HGOs at the level of each chromosome and of the whole genomes can be found in "supporting information part 2". The detailed data related to the 3 whole genomes shows the various distances and errors between real computed HGOs for each genome and theoretical HGO optimum value = 0.6909830055. Particularly, it is found that the 3 HGOs calculated for the respective 3 genomes of Neanderthal, Sapiens (2003 Build34 and 2013 hg38 Sapiens) are very close to the ideal theoretical optimal HGO =0. 6909830056 ( 99.67% for the least optimal genome).

It is also observed that female genomes (XX) are more optimal than male genomes (XY). On the other hand, the genomes of Neanderthal and Sapiens (Build34 of 2003) have very close optimization levels. We believe these results from the fact that the precisions of their respective DNA sequencing are similar. On the contrary, the hg38 genomes of 2013 show the most optimal levels, this is most certainly due to the deeper quality of their DNA sequencing. Figure 1 summarises HGO results for these 3 human genomes of varying levels of evolution. Table 6 in "supporting information part 2" summarizes the HGO values, absolute and relative errors in both cases of man or human whole genomes for the 3 human genomes compared.

HGO spectral hierarchy of the 24 Human chromosomes

The following Figures illustrate the hierarchical spectrum of the individual HGOs of each of the 24 chromosomes for each of the three genomes analyzed. It should be noted that the upstream / downstream tipping point lies between chromosomes 14 and 21, which is closely related to the probable mechanisms explaining trisomy 21 (whose disorders involve precisely these two chromosomes). Finally, we note that it is the downstream region that contributes the most to the superiority of optimality of sapiens hg38 compared to sapiens Build34. However, a more detailed analysis of the upstream and downstream regions shows that when passing from sapiens Build34 2003 to hg38 2013, the notorious optimization obeys the global strategy law of the LOH. Also of note is that 20 out of 24 chromosomes are OK, with the exception of chromosomes 13, X, Y, and 1. The law presented here states that there is reduction of optimality for upstream chromosomes and improvement of optimality for downstream regions.

It is therefore remarkable that this is the same and only law which seems to simultaneously control two domains as different as: 1) the global strategy of LOH deletions of tumors on the one hand and 2) the difference of evolution of the same genome following two increasing precision levels of DNA sequencing (Build34 2003 and hg38 2013) on the other! In "supporting information part2, Tables 7- 9" (HGO spectral hierarchy of the 24 Human chromosomes:

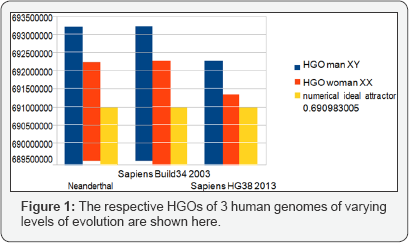
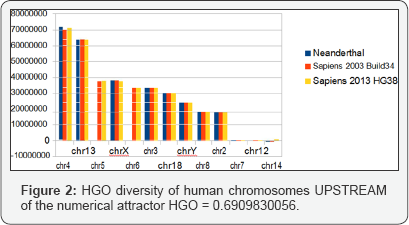
Detailed values for HGO chromosomes spectral hierarchy for the 3 Human genomes), we have sorted the 24 chromosomes by increasing values of CG/TA ratios in the 3 cases of compared genomes. It then reveals a hierarchical classification scale of 24 chromosomes ranging from 1 / Phi (chromosome4) to 3/2 Phi (chromosome 19) (Figures 1-3).

HGO Disturbed by 240 LOH deletions related to 5 different Chromosomes and 5 different Tumors

After demonstrating how 3 human genomes with increasing levels of sequencing quality and evolution accuracy seem to “fit” this theoretical value of HGO, we will now analyze how small mutations on one of the chromosomes can "disrupt" this HGO. For this purpose there are a very large number of publications associating such nucleotide regions with deletions of the chromosomal DNA of different tumor cells. We analyzed the Loss of Heterozygosity associated with 240 cases published in [20-25]. These 240 cases relate successively to the Breast [20,21], Glioblastoma [22], Colorectal [23], Neuroblastoma [24], and Prostate [25] cancers. They successively affect the chromosomes 13, 5, 10, 1 and 16.

This exhaustive analysis will then reveal the following generic law:

"When an LOH deletion affects a chromosome upstream of the HGO point (chromosomes 4 13...) in the chromosomal spectrum, this deletion degrades the genomic optimum of the cancer genome. When an LOH deletion affects a chromosome downstream of the HGO point (chromosomes 19 22...) In the chromosomal spectrum, this deletion improves the genomic optimum of the cancer genome. The full details of these analyses are available in « Part 3 - The 240 analyses detailed from 6 independent publications concerning 5 different types of cancer and 5 different chromosomes ». Table 3 below summarizes these results (Table 3).

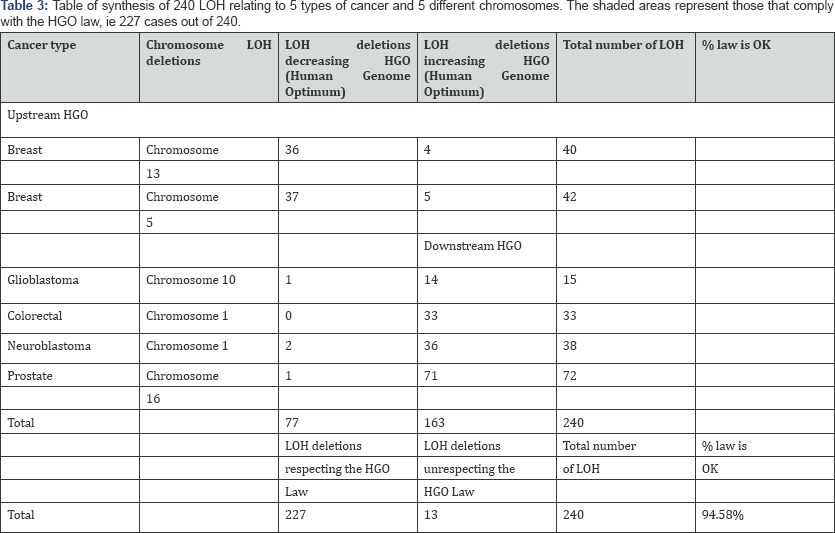
In the Table 1 the shaded areas represent cases ofLOH complying with the generic rule, while the unshaded areas represent cases of LOH that do not comply with this rule. In total, 227 cases respect the rule and only 13 cases of LOH do not respect it, a success rate of this law equal to 94.58%. In « Bold » we represented the 153 Breast and prostate LOH deletions cases detailed in this article.

Global Graphical Analysis of the 240 LOH Tumor Cases

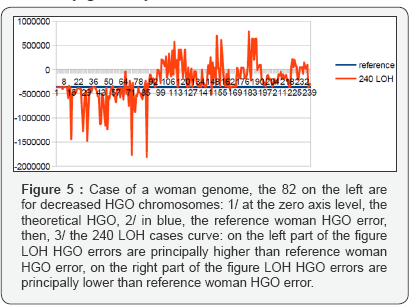
In Figure 2 below, the 4 images 2A-2D. below present an overall analysis of the HGOs resulting from the 240 cases of LOH deletions associated with 5 types of cancers and 5 distinct chromosomes.

For this purpose we recall how to distinguish 3 types of HGO:

The theoretical HGO: (3-Phi)÷2 = 0.6909830055, where Phi is the « golden ratio » Phi = 1.618033...

The 2 reference HGOs relating to the respective hg38 reference genomes of the female (0.691347793)

and man (0.692286423). -The 240 HGOs relating to each of the 240 chromosomes having ubi LOH deletions. On the other hand, the chromosomes are presented in these 4 figures according to the order sequence of the hierarchical spectrum shown in Figure 1.

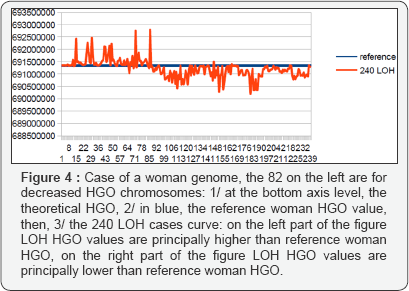
Consequently, these 240 cases are presented in the order of upstream towards downstream with respect to the theoretical HGO. In particular, this is the case for the first 82 LOHs for breast tumors affecting chromosomes 13 and 5, both of which are upstream, on the contrary, all remaining LOHs will be downstream (Fig. 1C) of the theoretical HGO point, thus downstream. Thus, Figure 2 will synthesize the relative positions of all these HGOs. Similarly, the errors or distances Figure 2 will also be calculated relative to the respective distances between HGO of the 240 cases of LOH deletions, or of the reference HGOs, with respect to the HGO theoretical (Figures 4-7).

Discussion

We have successively demonstrated that, in the Human Genome Evolution and in the precision of sequencing of the genomes, these genomes seemed to "seek” a sort of numerical optimum: HGO.Then, we demonstrated how the LOH deletions affecting the tumor cell chromosomes obeyed a generic law based on the chromosome hierarchization illustrated in Figure 1. However, an important open-ended question: do these LOH deletions affecting the HGO optimum have any potential significance for the pathogenicity and aggressiveness of these tumors? This is what we are going to demonstrate now.

First Analysis: 40 Breast tumors LOH in Chromosome 13

A. Basic Data

The article supporting our analysis:

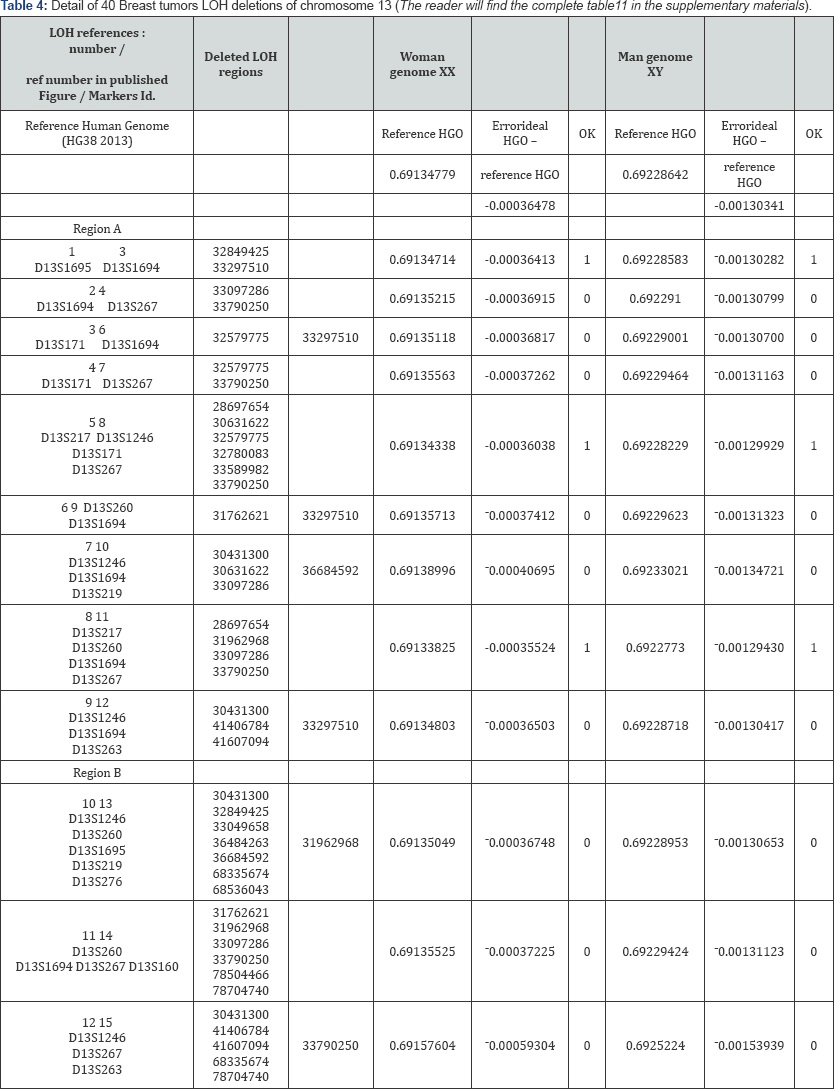
We analyze here 40 LOH associated with Breast cancer of chromosome 13 from the publication:

Eiriksdottir G. et al. [20] Mapping loss of heterozygosity at chromosome 13q: loss at 13q12-q13 is associated with breast tumour progression and poor prognosis, Of the 46 LOH cases published; only 40 cases of exploitable LOH were identified. Indeed some LOH are reduced to a single marker that is to say approximately 200000bp, which is too insignificant. For example,Table 11 the first of the markers in this study is D13S1695: chr13: 32,849,425-33,049,658 200,234 bp. However, such a length of 200234 bp is too insignificant.

We therefore retain only the LOHs corresponding to regions delimited by 2 markers (for example the first LOH referenced 13 in table 11), as well as regions comprising at least 2 markers alone (for example the LOH referenced 36 41 comprising 4 Markers alone). The chromosome support of our analysis:

chr13:1-114,364,328 114,364,328 bp

https://genome.ucsc.edu/cgi-bin/s?db=hg38&lastVirtModeTy pe=default&lastVirtModeExtraState=&virtModeType=default&vir tMode

= 0& nonVirtPosition = &position = chr13⁰%3A1-

4328&hgsid=544158480_4gTu7ZinG6Wue6eggFsvNZ387C0p

The supporting figure of our analysis (Figure 8).

B. Basic Results

( Table 4)

C. To Conclude

Recall that chromosome 13 is upstream with respect to the tipping point HGO (manuscript Figure 1). Thus, according to our "global strategy law of LOH by chromosomes", the majority of LOH "should" degrade the value of the HGO: in effect, we observe that 36 out of 40 cases degrade the HGO.

D. Second analysis: 42 Breast tumors LOH in Chromosome 5

Details in supporting information Table 4.

a. Basic Data

The article supporting our analysis.

In the analysis from Hrefna K. Johannsdottir et al. [21] Chromosome 5 imbalance mapping in breast tumors from BRCA1 and BRCA2 mutation carriers and sporadic breast tumors, Int. J. Cancer: 119, 1052-1060 (2006) ' 2006 Wiley-Liss, Inc, http:// onlinelibrary.wiley.com/doi/10.1002/ijc.21934/pdf

chromosome support of our analysis:

chr5:1-181,538,259 181,538,259 bp.

https: //genome.ucsc.edu/cgi-b in/hgTracks? db=hg 38&lastVirtModeType=default&lastVirtModeExtraState

= &virtModeType = default&virtMode = 0&nonVirtPositio n=&position=chr5%3A1-1538259&hgsid = 490730839 uVDpPnDat9B5Obik1m1EEO17KXGd

The supporting figure of our analysis (Figure 9).

E. Basic Results (Table 5)

a. To Conclude

Recall that chromosome 5 is upstream with respect to the tipping point HGO (see manuscript Figure 1).. Therefore, by virtue of our "global strategy law for LOH by chromosomes", most LOHs "should" degrade the HGO value: in effect, 37 out of 42 cases degrade HGO.

b. Third analysis: 72 Prostate tumors LOH in Chromosome 16:

Details in supporting information Figures 5 & 6.

F. Basic Data

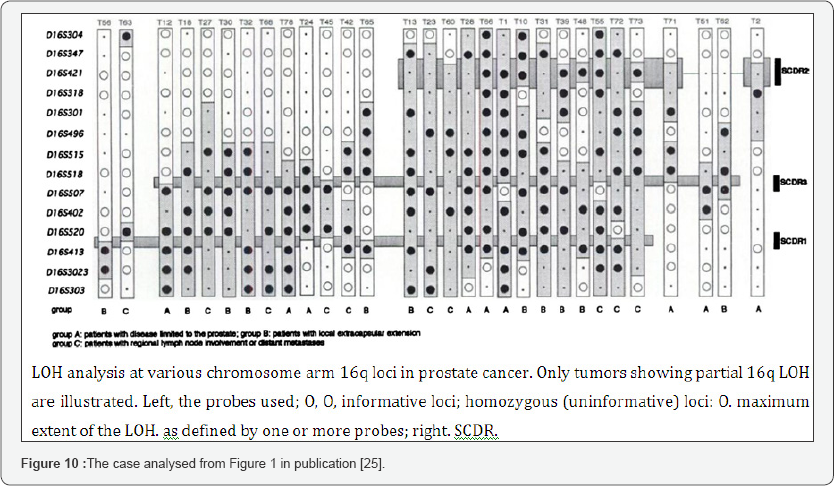
The article supporting our analysis:

Latil A. et al. [25] Loss of heterozygosity at chromosome 16q in prostate adenocarcinoma: identification of three independent regions. , http://cancerres.aacrjournals.org/content/57/6/1058. long.

The chromosome support of our analysis: chr16:1-90,338,345 90,338,345 bp.

https://genome.ucsc.edu/cgi-bin/s?db=hg38&lastVirtModeTy pe=default&lastVirtModeExtraState=&virtModeType=default&vir tMode

=0&nonVirtPosition=&position=chr16%3A1-

90338345&hgsid = 512328625_ KTg3NgwGLbBBObaQAQwxFiLtKd10

The supporting figure of our analysis (Figure 10).

a. Basic Results (Table 6)

i. To Conclude

Recall that chromosome 16 is downstream with respect to the tipping point HGO (see manuscript Figure 1). Therefore, by virtue of our "global LOH strategy law by chromosomes", most LOHs "should" improve the HGO value: in fact, 66 cases out of 72 increase the HGO in the case of a Genome (XX) but 71 out of 72 cases increase HGO in the case of a male genome (XY).

Discussion

I. First analysis: 40 Breast tumors LOH in Chromosome

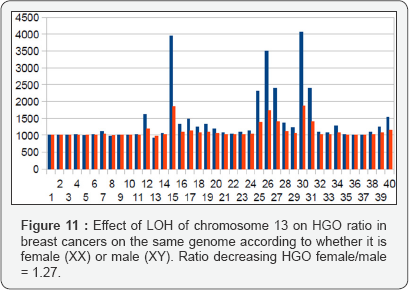
(Figure 10) Effect of LOH of chromosome 13 on HGO ratio in breast cancers on the same genome according to whether it is female (XX) or male (XY). Ratio decreasing HGO female/male = 1.27. In the analysis from publication (20), we show that HGO conforms to the above law in 36 of 40 cases (chromosome 13 is in the region upstream of the HGO point, Figure 1). In Figure 10, it is interesting to note that the effect on a female genome (XX) is greater than the effect on this same male genome (XY), which is in agreement with the fact that this cancer is almost exclusively feminine. A rapid analysis of the degradations of HGO - for the same LOH - depending on whether the genome is XY (masculine) or XX (feminine), will show that these expected degradations are 1.27 times higher in the case of a female genome (XX). This would reinforce the fact that the female genome is more sensitive to these LOH deletions than the male genome (Figure 11).

II. Second Analysis: 42 Breast tumors LOH in Chromosome 5:

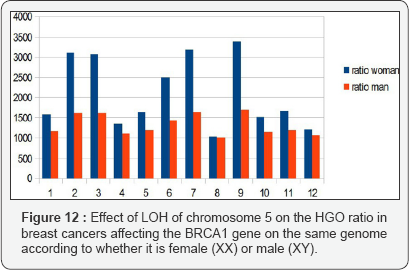
In the analysis from publication [21], we show (Figure 3) that the HGO conforms to the above-mentioned law in 37 cases out of 42 (chromosome 5 is located in the region upstream of the HGO point, (Figure 1). The analysis below concerns cases of LOH affecting BRCA1 mutations. It is interesting to observe - even if only visually - that the effect on a female genome (XX) is greater than the effect on the same male genome (XY), which is in agreement with the fact that this cancer is almost exclusively feminine (Figure 12).

III. Third analysis: 72 Prostate tumors LOH in Chromosome 16:

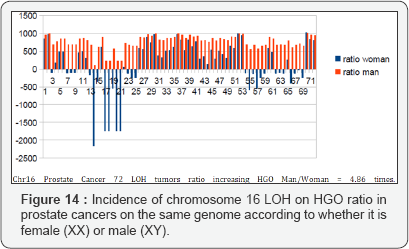
Of 72 cases analyzed from article [25], 71 cases IMPROVED HGO while only one did not (Chromosome 16 is located in the region downstream of the HGO point, Figure 1). The evaluation below analyzes the evolution of the HGO according to the 3 grades of pathogenicity of the tumors studied:

i.Grade A: patients with disease limited to the prostate.

ii. Grade B: patients with local extracapsular extension.

iii. Grade C: patients with regional lymph node involvement or distant metastases.

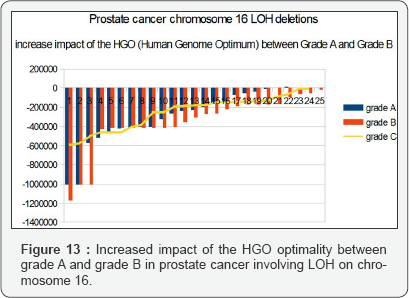
iv. Between Grade A and Grade B, an average HGO improvement of 4.88% was observed [26-29].

The graph below (Figure 13) illustrates this optimization. The HGO of grade C is of the same order as that of Grade A, which may be explained by the fact that the LOHs of grades A and B are generally monochromosomes whereas the LOHs of grade C are multichromosomes [30-36]. There are therefore more complexes to be demonstrated in monochromosome studies. It is interesting to note that the effect on a female genome (XX) is 4.86 times lower than the effect on the same male genome (XY), which is in agreement with the fact that this cancer is exclusively male (Figures 13 & 14).

Conclusion

It is remarkable to discover this strong correlation between the pathogenicity and the aggressiveness of tumors on the one hand, and the categorization and hierarchization of mutations LOH of the mutant genomes at the origin of tumors [37-42]. The law discovered here is universal, common to all types of cancers and to all chromosomes. Its nature is mathematical, proceeding only from the DNA information of the genomes. The method is exhaustive, systematic, and predictive, making it possible to anticipate the knowledge of the pathogenicity of an existing tumor or even of a mutation before the tumor disappears.

The mutant genome thus constitutes a kind of signature, virtual and numerical image of the tumor. Thus it is remarkable to discover that the LOH genome of a breast tumor, a cancer that is exclusively feminine by its nature, will lead to an overall HGO genomic degradation much greater than the same mutation affecting a male genome [43-48]. Conversely, it will be the same, but in the opposite way for a cancer of the prostate which, it is, exclusively masculine. Finally, in this same prostate cancer, the impact on HGO between grade A and grade B is significant: recall:

i. Grade A: patients with disease limited to the prostate.

ii. Grade B: patients with local extracapsular extension.

iii. Grade C: patients with regional lymph node involvement or distant metastases.

iv. Between Grade A and Grade B, an average HGO improvement of 4.88% was observed.

To conclude, the most important fact is the universal character ofthis HGO law, presented here for both breast and prostate cancers, the universal character of this law has been widely generalized experimentally on a large number of cancers differences affecting most chromosomes, this generalization will be described in. "The Human Genome Optimum" (HGO): Towards a Universal Law Controlling All Human Cancer Chromosome LOH Deletion (Loss of Heterozygosity) accepted for publication in the Global Journal of Medical Research [49].

a. We still have a lot to discover on this fascinating CODE that is DNA...

b. To conclude, it is difficult to fully understand the extent of this discovery:

c. -At the theoretical level it seems fascinating that there exists this perfect digital fit of the whole genome around this sort of digital attractor

d. At the theoretical level again, one will note the universality of the HGO law, which applies to ALL the cancers.

At the applied level, the correlation between this law and the increasing degrees of pathogenicity of the tumors is remarkable. It is thus well understood that the mechanism of invasive pathogenicity of a tumor is because its genome is more optimal than that of a healthy cell. Its immediate application is the prioritization of tumor pathogenicity stages. In this study we have just raised a new corner of sail on DNA and the human genome. A jump was the discovery of the fractal nature of DNA [2,28] or certain structures of the brain [29]. Thus, mathematics has become imbedded in genetics. Other mathematical approaches to genomes, which are equally original, are to be noted with approaches to matrix [30] or mathematical topology [31]. Then it is frankly a hypothetical « quantum theory of DNA information» that invites itself into DNA [32]. And, of course, there is the famous golden ratio and its Fibonacci numerical patterns. They're not only found in the rhythms of the heart and in the arborescence of our arteries [33], but also in the RNA [34] or in quantum physics [35].

Finally, like these different researchers, we have just demonstrated how the "CODES" [36] are at the heart of the mechanisms of Nature."Codes" real today ... "Codes" artificial tomorrow [37]. As demonstrated in [38], a substantial fraction of mutations in human cancer are attributable to random errors occurring during DNA replication. Therefore, we think that our « long range human genome law » controling cancer mutations are probably important... In [15, 39, 40-42,44-48] we will present other "hidden mathematical codes" that organize the DNA sequences of the human genome.

However, the major conclusion seems to be the following:

All the human genetic heritage is concentrated in 2 genomes: the nuclear genome and its 23 pairs of chromosomes on the one hand, and the small mitochondrial genome mtDNA, on the other hand. The majority of mutations associated with genetic diseases as well as all cancers most often lead to deletions affecting each of these 2 genomes [50-52]. Then, in the article "Sapiens mtDNA circular long-range numerical meta-structures are highly correlated with mtDNA diseases mutations" [39], as in the present article, we demonstrate that all these mutations unbalance, for both genomes, a kind of optimum of each of these genomes. This is probably the major result that we will have to continue to reflect on and experiment with. Finally, our approach may be related to these hundreds of unpredictable mutations resulting from manipulation of genomes by CRISPR revolutionary technology [43]. Effectively in their 2017 article, authors.

Note that « .../...They found that the technique had successfully corrected a gene that causes blindness in the mice, but the two mice that had undergone CRISPR gene-editing had sustained more than 1,500 unintended single-nucleotide mutations, and more than 100 larger deletions and insertions.../...».

Acknowledgement

We especially thank Dr. Robert Friedman M.D. practiced nutritional and preventive medicine in Santa Fe, New Mexico, woldwide expert on Golden ratio Life applications (https://www.amazon. com/Golden-Ratio-Lifestyle- Diet-Potential/dp/0975280252). We also thank the mathematician Pr. Diego Lucio Rapoport (Buenos aires), the french biologist Pr. Francois Gros (Pasteur institute, co-discoverer of RNA messenger with James Watson and Walter Gilbert ) and Pr. Luc Montagnier, medicine Nobel prizewinner for their interest in my research of biomathematical laws of genomes.