Abstract

To continue with a previous publication, constrained evolutionary algorithms for IN-VITRO-BED-LQ model (Linear Quadratic Biological Effective Dose Model) in prostate cancer Hyperfractionation radiotherapy TPO were optimized with Pareto-Multiobjective (PMO) methods. This study improves for IN-VIVO-BED-LQ that research with a further comparative between in vitro and in vivo results optimization followed by a precision-refinement with Interior Optimization (IO) methods. Complex software is developed based on hyperfractionation constraints, but within vivo main parameters dataset, and IO programming. Results with software design algorithmic method take in handle subroutines functions and matrix-algebra method for setting constraints and 3D IO surfaces. Results with 3D Interior Optimization by using the Genetic Algorithms (GA) previous numbers show that they get very good precision with new invention of isodoselines sharp determination. Solutions dataset is short compared with previous in vitro study. Findings prove comparative PMO 2D imaging charts and numerical values of PMO prostate cancer hyperfractionated TPO parameters. Applications for prostate tumors radiotherapy planning, especially with new Surfactal-Isodoselines, brain prostate metastases and stereotactic radiosurgery treatments are briefed.

Keywords: Pareto-Multiobjective Optimization (PMO); Mathematical Methods (MM); Biological Models (BM); Radiation Therapy (RT); Initial Tumor Clonogenes Number Population ( N0 ); Effective Tumor Population Clonogenes Number ( NEffective ); Linear Quadratic Model (LQM); Integral Equation (IE); Tumor Control Probability (TCP); Normal Tissue Complications Probability (NTCP); Biological Effective model (BED); Tumor Control Cumulative Probability (TCCP); Radiation Photon-Dose (RPD); Nonlinear Optimization; Interior Optimization (IO); Radiotherapy Treatment Planning Optimization (TPO); Nonlinear Optimization; Treatment Planning Optimization (TPO); Artificial Intelligence (AI); Pareto-Multiobjective Optimization (PMO); Genetic Algorithms (GA)

Introduction And Objectives

From a previous publication, [98,100], the objective of this contribution is applying Constrained Genetic Algorithms and 3D Interior Optimization on radiotherapy BED-LQ model for prostate tumors [1-24,87-94] with vivo dataset for a hyper fractionated schedule. The BED-LQ model [1-24,40,74-79,87-94], is useful for low dose fractions, while LQL and PTL ones are more appropriate for high dose delivery RT treatment schedules, namely, hypo fractionated treatment [94]. The numerical difference between in vitro LQ parameters for prostate LQ model can be considered important [1-24,40,74-79,87-100]. It is not subject of this article any discussion about hyper fractionation versus hypofractionation dose delivery. Prostate cancer epidemiology statistics-figures are within the group of highest incidence-prevalence cancers, but lower than lung and breast tumors, [99]. Therefore, the objective of the study is to carry out a double optimization process. Firstly, 2D GA optimization with vivo data for LQ models. Secondly, making the most of the first GA obtained results, to get an improved refinement by using 3D Interior Optimization methods. Numerically, TPot magnitude difference in vivo values, prostate cancer, are about 28 days in vivo and [2,19] in vitro ones are lower. In general, both in vitro and in vivo TPot parameters for prostate tumors are greater than other types of cancer [20- 25]. This fact implies a longer survival time with several proper characteristics related to different treatment stages. Namely, surgical, RT, radio surgical, chemotherapy, immunotherapy, hormonal therapy, combinations of all of them. Today, biomarkers are playing an important role in order to predict the survival time, optimal chemotherapy, and both characteristics at the same time [95]. Table 1.1 shows biomarkers classification into P-Biomarkers (Biomarkers for Prognosis, [96]), T-Biomarkers (Biomarkers for Optimal Treatment), and H-Biomarkers (Hybrid Biomarkers Group), [Author’s proposal].

Prostate Cancer Bed Model Parameters For In Vitro And In Vivo Optimization

The parameters differences between both simulations are set in Table 1, A (in vitro) and B (in vivo). Note that these numerical disparities yield towards different optimization results for propagation of increments along the computational optimization. Table 1-B.-IN VIVO Software implemented dataset for GA programming with source references [38,43-45]. Note the intervals for pareto objectives differences. The programming design has two parts: Nonlinear GA-PMO engineering software with matrix algebra constraints, similar to the previous publication in codes/patterns for PMO-BED models. The second part is rather more difficult. That is, 3D Interior Optimization with the new useful-practical finding of isodose lines for radiotherapy planning hyper fractionated schedule. Those new Isodose lines along the Interior Optimization surface constitute a TPO advance and innovation of this contribution. Results comprise Graphical and Numerical TPO hyper fractionated RT treatment planning. 2D GA graphics are presented in several formats, for 100, 150, and 250 generations. 3D Interior Optimization charts are illustrated with Isodoselines, optimal areas, and numerical data inset. Numerical results show first GA figures and Interior Optimization refined values. Therefore, the novelty of this article, based on the previous evolutionary optimization paper, [98], is its GA algorithms and computational optimization with in vivo parameters, 3D Interior Optimization improvements, and the practical definition of 3D Isodoselines for RT planning hyperfractionated schedule. It is objective, according to the precision of numbers obtained, that the mathematical and software developed is considered appropriate. Grosso modo, a double constrained optimization based on previous Nonlinear Pareto-Multiobjective GA optimization was developed with the addition of 3D Interior Optimization refinement and the new-practical Isodoselines definition. Applications for radiotherapy hyperfractionated BED-TPO planning are presented. Numerical Analysis precision results are gonna be promising for improvements of the method.

Mathematical And Computational Methods

Following previous studies, mainly the prostate cancer one [98], and publications for Breast, Head-Neck cancer, here the Pareto-Mult objective Optimization Fowler-foundation BED Effective model was programmed, [1-24,40,68,74-79,87- 94,98,99]. Alpha, Betha, and rest of parameters intervals are detailed in Table 2. Algorithms 1-5 set the 2D GA and 3D IO formulas and constraints [85-88]. Radiobiological parameters Alpha and Betha are implemented independently, not in quotient [alpha/beta] because of the programming pattern’s purpose. This low-dose LQ-BED model constitutes the foundations for hyper fractionated radiotherapy TPO, though there are dissimilarities among authors [20-25]. Therefore, the Pareto-Mult objective [Algorithm 1] that was set, with Chebyshev L1 norm, [Algorithms 2-4] is presented firstly. The IO method is explained secondly.

Evolutionary Algorithms Mathematical Method

The GA algorithms used are approximately the same than in previous prostate cancer publication, [98]. The sequence of the formula’s development is as follows,

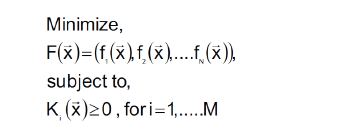
(Algorithm 1)
where
F(x): Main function to be optimized.
fi (x): Every function of same variables (x).
Ki (x): Constraints functions such as in general N ≠ M.

BED nonlinear-quadratic model has been adapted for in vivo parameter TPot magnitude. Then, PMO in Prostate, [24,88,89,98] tumors simplest BED model reads,

(Algorithm 2)
where,
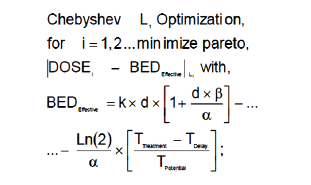
BED: The basic algorithm for Biological Effective Dose initially developed by Fowler et Al. [22-25, 89-94,98].
k: Optimal Number of fractions for hyperfractionated TPO. Optimization parameter [22-25,89-94,98].
d: Optimal Dose magnitude for every fraction. Optimization Parameter [Gy]. [22-25, 89-94].
α: The basic algorithm constant for Biological Effective Dose models. Radiobiological experimental parameter in vivo. [Gy-1]. [22-25, 89-94].
β: The basic algorithm constant for Biological Effective Dose models in vivo. Radiobiological experimental parameter. [Gy-2]. Note that it is very usual to set in biological models [ α / β in Gy].
TTreatment: The overall TPO time. This parameter varies according to authors’ and institutions/hospitals criteria. [22-25, 89-94,98].
TDelay: The overall TPO time delay for clonogens re-activation. This parameter varies according to authors’ experimental research.
TPotential: The potential time delay for tumor cell duplication. This parameter varies according to authors’ experimentaltheoretical research.
DOSE: The dose magnitudes for lung cancer simulation algorithm for Biological Effective Dose [22-25, 89-94,98 ]. Software patterns were calculated around intervals prostate DOSE ϵ [70,78] Gy.

Algorithm 1 [Fowler mainly, modified by Casesnoves, [98]. Prostate PMO algorithm [1-25,85-90] implemented in software. Table 2 shows these intervals for optimization parameters details. Programming was developed in Matlab® system. At programming trials, it was found that precision was increased related to in vitro parameters [98]. The constraints algebraic algorithm developed for Pareto-Multiobjective problem, [Algorithms-3-5, Casesnoves 2023] reads,

(Algorithm 3)
where
SLOWER: Summatory of all lower constraints for parameters [K, d, T].
SUPPER: Summatory of all upper constraints for parameters [K, d, T].
Ki: Dose fraction number parameter for [i = 1, 2].
di: Dose fraction magnitude parameter for [ i = 1, 2].
TTREATMENT: Treatment time magnitude parameter for [i = 1, 2].

The subroutines programming strategy, as in [98], which are implemented reads,

(Algorithm 4)
where,
SK,d,T: Upper (maximum) and Lower boundaries for parameters [K, d, T], according to Algorithms 1-2.

Algorithm (5)
where all the parameters description are at Algorithms 1-4.

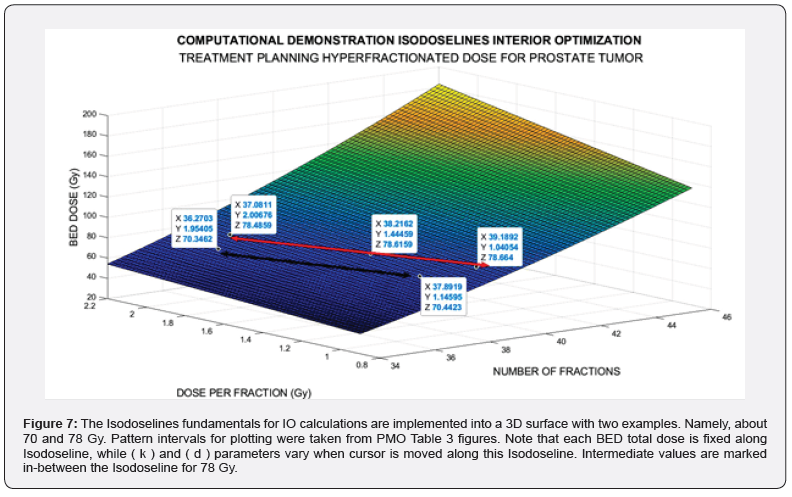
An image processing showing the utility for PTO of this IO with several Isodoselines is presented, Figure 7. Note that Algorithm 5 is converted when running software in a nonlinear-quadratic system of equations.As it is quadratic, the rationale of the precise results is justified.

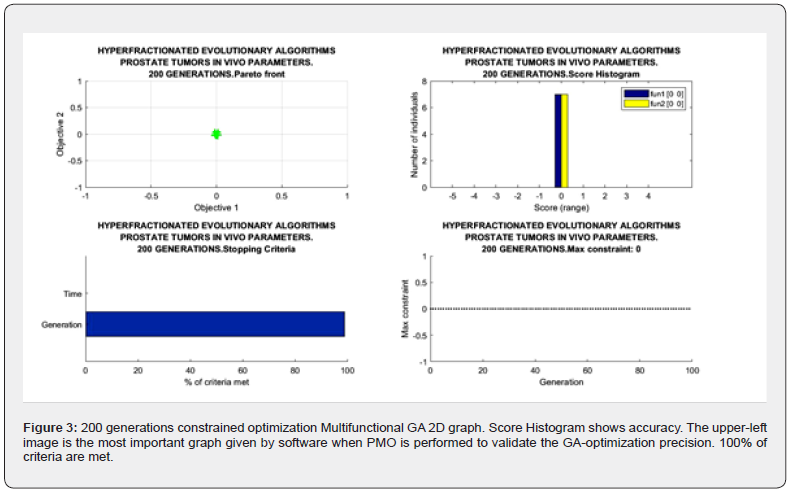
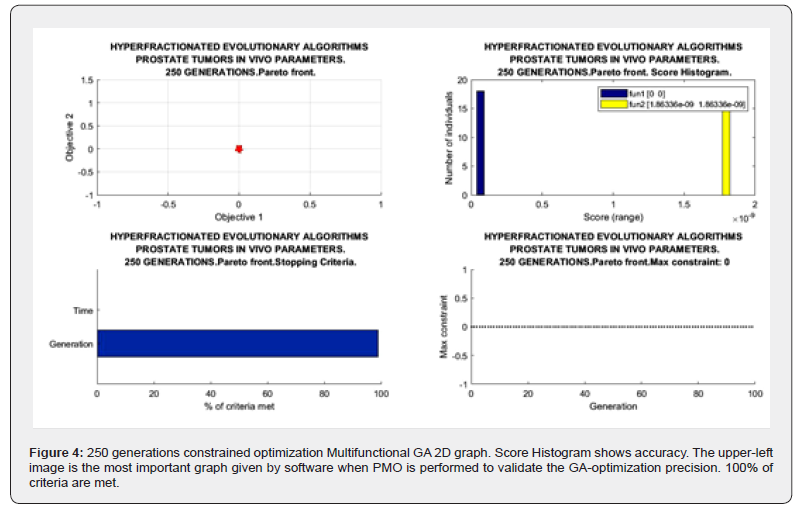
Sofware used for this study continues previous algorithms papers [1-20,24,68,74,88,89,98] with modifications, and addition of IO programs. For GA-PMO modeling, Equation 1 and Algorithms 1-4 are implemented on 2D programs, with application of Algorithm 5 basic model formula. Algorithm 2 was programmed with Algorithm 3 matrix constraints subroutines-functions. Table 2 shows Constrained GA Optimization in vivo parameters, different from [98], implemented in Algorithms 1-5. From Table 3 results, after IO implementation, 3D IO dataset for Table 4 is got. From all these numbers, 3D IO and 2D Genetic Algorithms Graphical Optimization imaging-processing charts, error determinations, pareto-distance, get precise approximations for hyperfractionated PMO-BED model. In general, the precision obtained is more than expected Tables 3-4.

Interior Optimization Computational Method

3D Interior and Graphical Optimization methods are used to confirm and refine the in vivo precision of the GA results from [98]. This is an advance as it was found that by using Interior Optimization the precision is increased and Isodoselines can be set for TPO. The method and software developed is a potential new application for accurate TPO.

Programming Dataset

Table 2 shows Matlab Constrained GA optimization dataset is detailed, for first optimization stage. As in [98], constraints matrix algebra is implemented through [Algorithms 3-5]. All these simulation techniques come from [20-25,68,74,75,80,81,85- 94,98]. The in vivo TPotential in prostate cancer for setting data is TPotential ϵ [26,30] days. The reason to use vivo dataset in this second prostate study is that, although currently the vivo radiobiological differences differ in literature, more realistic results are gonna get.

2d Evolutionary Algorithms Optimization Results

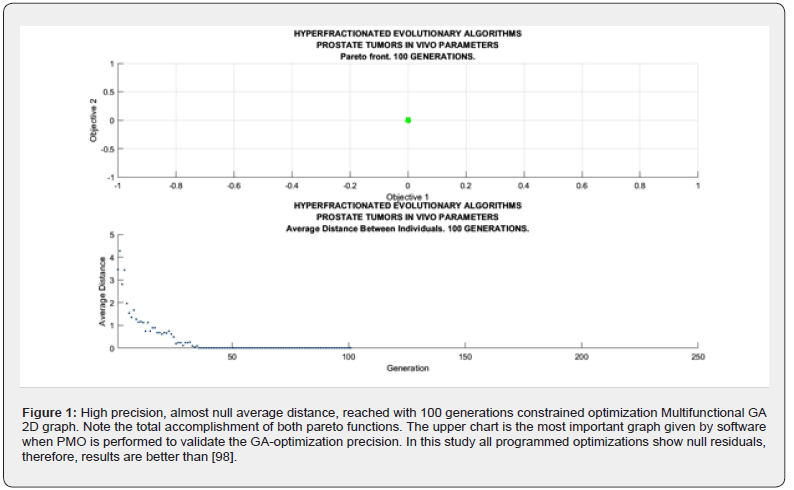
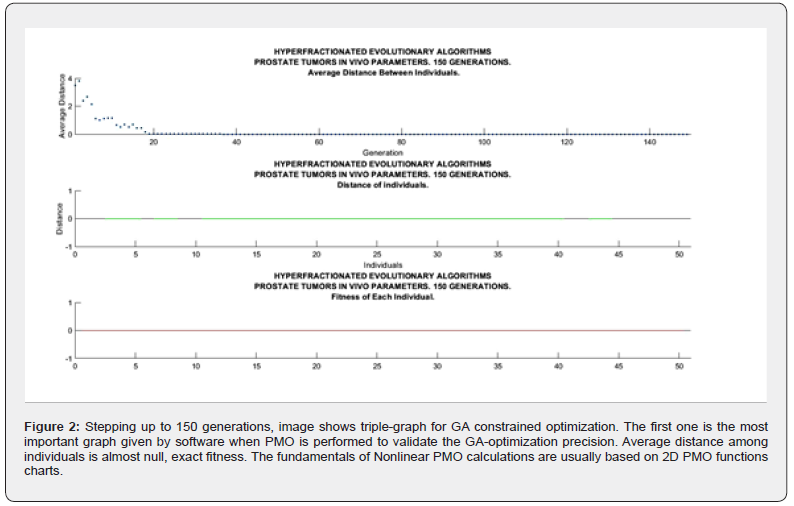
2D GA Graphical results are shown in Figures 1-4. The constrained optimization results are presented sharply in 2D multifunctional charts. This constrained optimization with in vivo parameters, [Algorithms 1-5] gets better results than in vitro one in the previous prostate cancer study [98].

3D Interior Optimization Results

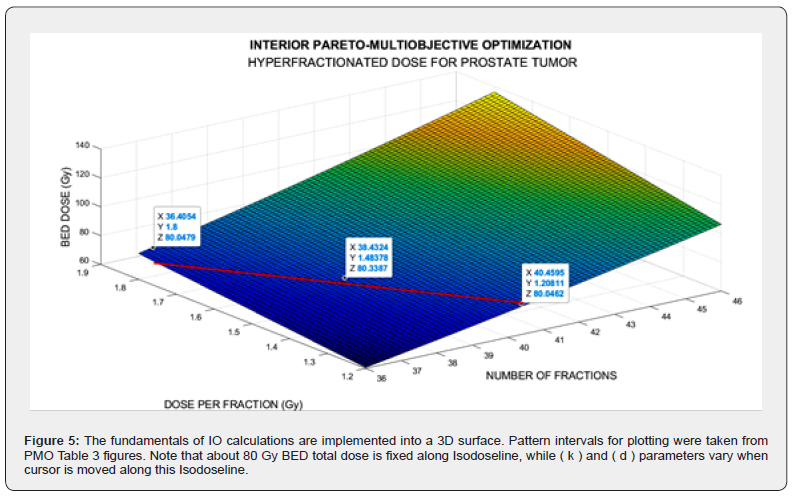
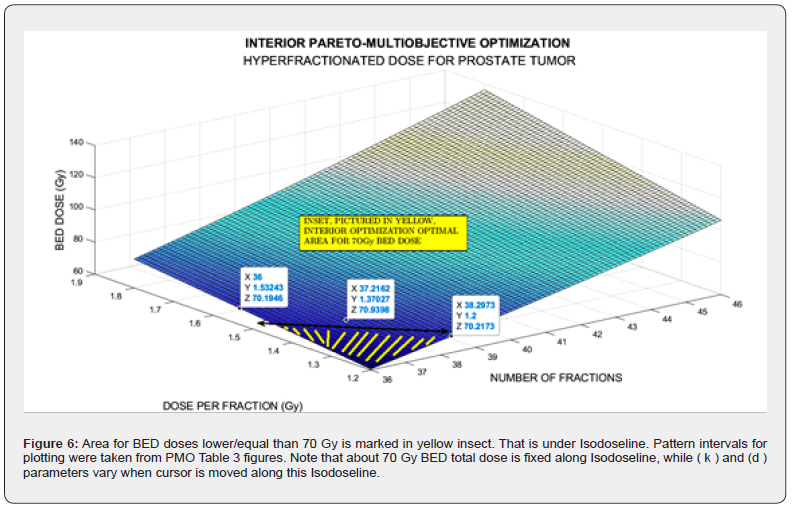
The imaging process software shows the results got with 3D Interior Optimization, Figures 5-7. Results are very acceptable. Isodoselines are marked inset every image. The radiotherapy planner gets multiple choices by using this 3D IO method.

Invention of Interior Optimization Isodoselines

When performing the 3D Interior Optimization refinement, it was found that Isodoselines can be feasible and useful. Figure 7 can be considered a definite demonstration. It shows several selected Isodoselines for several TPO-dose magnitudes to prove the new utility found. For IO, the algorithm to be set on program patterns reads.

Numerical Results

Numerical results can be divided into two parts. First one is the GA numerical figures, Table 3. Secondly IO results briefly based on Figure 7 mainly. In Figure 7 Isodoselines demonstrate their efficacy for TPO choice. That is, once fixed total dose, e.g., 70 or 78 Gy, any planner can select the desired number of fractions, and the convenient figure of fraction-dose along a Isodoseline, Figure 7 proof.

Genetic Algorithm Optimization Numerical Results

Figures for constrained PMO-GA optimization numerical data are presented shown in Table 3. As occurred in [98], constrained optimization displays acceptable numbers within numerical intervals [1-24,40,68,74-79,87-94,98].

Interior Optimization Optimization Numerical Results.

Table 4 shows the accurate numerical results received with IO refinement method. Example-dataset included comes from Isodoselines of Figure 7.

Radiotherapy Treatment Planning Applications

Table 5 presents details and applications of both optimization techniques. Radiotherapy hyper fractionated treatment planning applications for prostate tumors are specified. Medical Physics principal applications for radiotherapy research emerge from the data.

Discussion And Conclusions

The objective of the study was to apply firstly constrained 2D GA Optimization for prostate cancer hyperfractionated RT treatment with BED-LQ model and in vivo parameters. Secondly to get precise numbers by using 3D Interior Optimization methods. Constrained PMO-Multiobjective method was programmed with subroutines. A rather difficult software for 3D Interior Optimization to determine optimal surfaces and Isodoselines was designed. In general, for the first stage, the previous publication algorithms were set. The first part of the results comprises a group of 2D GA plots and numerical dataset. Constrained Optimization with Algorithms 1-5 got to get a Pareto Distance almost exact, null, with 250 generations. Interior Optimization application in second stages resulted in the invention of Isodoselines along the optimal surface, also with accuracy, Figure 7. These Isodose lines give many alternatives in terms of number of fractions and magnitude of fractions keeping the same total BED dose. It is considered a practical invention for RT planning with BED models. When the number of generations increases from 100, the running time of the constrained programs rises to approximately 1-3 minutes. As a rule, numerical and graphical results are better than expected. One of the reasons why GA-in vivo parameters method gonna get such precision, is the parameter magnitude of TPot in vivo. The second part of BED equation becomes lower, and the model results almost become a quadratic nonlinear equation with k and d variables. As a result, GA Optimization is simpler for computation and reaches more computational precision. The method can be considered somehow laborious, but the precision gained results are justified. Inconvenient is the increase of running time when using GA in direct proportion to the increment of generations number. The software to construct precise 3D Interior Surfaces and Isodoses has to be checked and done carefully. Grosso modo, a prostate cancer constrained RT-BED hyperfractionation model with GA and in vivo data was performed with Pareto-Optimization and refined with 3D Interior Optimization. Isodoselines constitute a practical result for BED RT accurate planning. Applications for prostate tumors and radiation therapy in general optimal TPO emerge from all the study.

Author’s Biography

Dr Francisco Casesnoves earned the Engineering and Natural Sciences PhD by Talllinn University of Technology (started thesis in 2016, thesis Defence/PhD earned in December 2018, official graduate Diploma 2019). He works as independent research scientist in computational-engineering/physics, and actually is Director of Independent Bioengineering Laboratory. Dr Casesnoves earned MSc-BSc, Physics/Applied-Mathematics (Public Eastern- Finland-University, MSc Thesis in Radiotherapy Treatment Planning Optimization, which was developed after graduation in a series of Radiation Therapy Optimization-Modelling publications [2007-present]). Dr Casesnoves earned Graduate-with-MPhil, in Medicine and Surgery [1983] (Madrid University Medicine School, MPhil in Radioprotection Low Energies Dosimetry [1985]). Casesnoves resigned to his original nationality in 2020 for ideological reasons, anti-monarchy-corruption, democraticrepublican ideology, and ethical-professional reasons, and does not belong to Spain Kingdom anymore. His constant service to the International Scientific Community and Estonia Republic technological progress involves about 100 DOI articles, more than 120 total publications, and about 4 books. Recent advances published are Superconductors Mathematical Modelling and Radiotherapy Brain Neurobiological Models, 3D-AI Isodosezones and Isodoselines. Among Dr. Casesnoves inventions and scientific creations are:
1. Numerical Reuleaux Method.
2. Radiotherapy Omega Factor correction for AAA model wedge filters dose delivery.
3. Integral-Differential materials erosion model.
4. Graphical Optimization.
5. Interior Optimization Methods.
6. Superconductors Molecular Effect Model.
7. Superconductors Multifunctional Transmission Line.
8. BED radiotherapy model GA and Graphical Optimization Isodoselines and Isodosezones.

Scientific Ethic Standards

Formulas applied/included are from previous prostate article with in vitro data. Model is a modification from several authors, based also on [20,24,25,83,88,89] techniques. Mathematical Algorithms 1-4 formulas are modificated from previous publications [20,24,25,83,88,89,100]. RT applications methods for these publications were created by Dr Casesnoves in 2021- 2. Methods from [20,87,88,100] were created by Dr Francisco Casesnoves in 3rd November 2016, and Interior Optimization Methods in 2019. BED model setting in Algorithms and programming were developed by Dr Casesnoves from previously published BED models. This article has previous papers’ information, from [1-21], whose inclusion is essential to make the contribution understandable. This study was carried out, and their contents are done according to the International Scientific Community and European Union Technology and Science Ethics [38,43-45]. References [38,43,44,45]: European Textbook on Ethics in Research’. European Commission, Directorate-General for Research. Unit L3. Governance and Ethics. European Research Area. Science and Society. EUR 24452 EN. And based on ‘The European Code of Conduct for Research Integrity’. Revised Edition. ALLEA. 2017. This research was completely done by the author, the computational software, calculations, images, mathematical propositions and statements, reference citations, and text is original for the author. When a mathematical statement, algorithm, proposition or theorem is presented, demonstration is always included. When a formula is presented, all parameters are detailed or referred. If any results inconsistency is found after publication, it is clarified in subsequent contributions When a citation such as [ Casesnoves, ‘year’] is set, it is exclusively to clarify intellectual property at current times, without intention to brag. The article is exclusively scientific, without any commercial, institutional, academic, religious, religious-similar, non-scientific theories, personal opinions, political ideas, or economical influences. When anything is taken from a source, it is adequately recognized. Ideas and some text expressions/sentences from previous publications were emphasized due to a clarification aim [38, 43-45,100].

References

1. Casesnoves F (2022) Radiotherapy Wedge Filter AAA Model 18 Mev- Dose Delivery 3D Simulations with Several Software Systems for Medical Physics Applications. Applications. Biomed J Sci & Tech Res 40(5).
2. Casesnoves F (2016) Mathematical Exact 3D Integral Equation Determination for Radiotherapy Wedge Filter Convolution Factor with Algorithms and Numerical Simulations.Journal of Numerical Analysis and Applied Mathematics 1(2): 39-59.
3. Casesnoves F (2015) Radiotherapy Conformal Wedge Computational Simulations,Optimization Algorithms, and Exact Limit Angle Approach. International Journal of Scientific Research in Science, Engineering and Technology (IJSRSET) 1(2): 353-362.
4. Casesnoves F (2019) Improvements in Simulations for Radiotherapy Wedge Filter dose and AAA-Convolution Factor Algorithms. International Journal of Scientific Research in Science, Engineering and Technology (IJSRSET) 6(4): 194-219.
5. Casesnoves F (2011) Exact/Approximated Geometrical Determinations of IMRT Photon Pencil-Beam Path Through Alloy Static Wedges in Radiotherapy Using Anisothropic Analytic Algorithm (AAA). Peer-reviewed ASME Conference Paper. ASME 2011 International Mechanical Eng Congress. Denver. USA. IMECE2011-65435.
6. Casesnoves F (2012) Geometrical Determinations of Limit angle (LA) related to maximum Pencil-Beam Divergence Angle in Radiotherapy Wedges. Peer-reviewed ASME Conference Paper. ASME 2012 International Mechanical Eng Congress. Houston. USA. IMECE2012-86638.
7. Casesnoves F (2013) A Conformal Radiotherapy Wedge Filter Design. Computational and Mathematical Model/Simulation’. Peer-Reviewed Poster IEEE (Institute for Electrical and Electronics Engineers), Northeast Bioengineering Conference. Syracuse New York, USA. April 6th, 2013. Peer-Reviewed Poster Session on 6th April 2013. Sessions 1 and 3 with Poster Number 35. Page 15 of Conference Booklet Printed.
8. Casesnoves F (2014) Mathematical and Geometrical Formulation/Analysis for Beam Limit Divergence Angle in Radiotherapy Wedges. Peer-Reviewed International Engineering Article. International Journal of Engineering and Innovative Technology (IJEIT) 3(7).
9. Casesnoves F (2014) Geometrical determinations of IMRT photon pencil-beam path in radiotherapy wedges and limit divergence angles with the Anisotropic Analytic Algorithm (AAA) Casesnoves, F. Peer- Reviewed scientific paper, both Print and online. International Journal of Cancer Therapy and Oncology 2(3): 02031.
10. Casesnoves F (2014) Radiotherapy Conformal Wedge Computational Simulations and Nonlinear Optimization Algorithms. Peer-reviewed Article, Special Double-Blind Peer-reviewed paper by International Scientific Board with contributed talk. Official Proceedings of Bio- and Medical Informatics and Cybernetics: BMIC 2014 in the context of the 18th Multi-conference on Systemics, Cybernetics and Informatics: WMSCI 2014 July 15 - 18, 2014, Orlando, Florida, USA.
11. Casesnoves F (2007) Large-Scale Matlab Optimization Toolbox (MOT) Computing Methods in Radiotherapy Inverse Treatment Planning’. High Performance Computing Meeting. Nottingham University. Conference Poster. 11(9).
12. Casesnoves F (2008) A Computational Radiotherapy Optimization Method for Inverse Planning with Static Wedges. High Performance Computing Conference. Nottingham University. Conference Poster.
13. Casesnoves F (2015) Radiotherapy Conformal Wedge Computational Simulations, Optimization Algorithms, and Exact Limit Angle Approach. International Journal of Scientific Research in Science, Engineering and Technology 1(2).
14. Casesnoves F (2015) Radiotherapy Standard/Conformal Wedge IMRT-Beamlet Divergence Angle Limit Exact Method, Mathematical Formulation, and Bioengineering Applications. International Article-Poster. Published in Proceedings of Conference. 41st Annual Northeast Bioengineering Conference. Rensselaer Polytechnic Institute. Troy, New York USA. P: 17-19.
15. Casesnoves F (2015) Radiotherapy Standard/Conformal Wedge IMRT-Beamlet Divergence Angle Limit Exact Method, Mathematical Formulation, and Bioengineering Applications. IEEE (Institute for Electrical and Electronics Engineers).
16. Casesnoves F (2015) Abstract-Journal. ‘Radiotherapy Standard/ Conformal Wedge IMRT-Beamlet Divergence Angle Limit Exact Method, Mathematical Formulation. International Conference on Significant Advances in Biomedical Engineering. 252nd OMICS International Conference 5(1). Francisco Casesnoves, J Bioengineer & Biomedical Sci 5: 1.
17. Casesnoves F (2001) Determination of absorbed doses in common radio diagnostic explorations. 5th National Meeting of Medical Physics. Madrid, Spain. September 1985. treatment Planning’ 11(9).
18. Casesnoves F (2001) Master Thesis in Medical Physics. Eastern Finland University. Radiotherapy Department of Kuopio University Hospital and Radiotherapy Physics Grouversity-Kuopio. Defense approved in 2001. Library of Eastern finland University. Finland.
19. Casesnoves F (2013) A Conformal Radiotherapy Wedge Filter Design. Computational and Mathematical Model/Simulation’. Peer-Reviewed Poster IEEE (Institute for Electrical and Electronics Engineers), Northeast Bioengineering Conference. Syracuse New York, USA. Presented in the Peer-Reviewed Poster Session on 6th April 2013. Sessions 1 and 3 with Poster Number 35. Page 15 of Conference Booklet.
20. Casesnoves F (2022) Radiotherapy Biological Tumor Control Probability Integral Equation Model with Analytic Determination. International Journal of Mathematics and Computer Research 10(8): 2840-2846.
21. Casesnoves F (2022) Radiotherapy Wedge Filter AAA Model 3D Simulations For 18 Mev 5 cm-Depth Dose with Medical Physics Applications”, International Journal of Scientific Research in Computer Science, Engineering and Information Technology (IJSRCSEIT) 8(1): 261-274.
22. Walsh S (2011) Radiobiological modelling in Radiation Oncology. PhD Thesis. School of Physics. National University of Galway.
23. Chapman D, Nahum A (2015) Radiotherapy Treatment Planning, Linear- Quadratic Radiobiology. CRC Press.
24. Mayles W, Nahum A (2015) Rosenwald, J. Editors. Handbook of Radiotherapy Physics. Second Edition. CRC Press.
25. Nahum A, Webb S (1993) A model for calculating tumour control probability in radiotherapy including the effects of inhomogeneous distributions of dose and clonogenic cell density. Physics in Medicine and Biology 38(6):653-666.
26. Haydaroglu A, Ozyigit G (2013) Principles and Practice of Modern Radiotherapy Techniques in Breast Cancer. Springer.
27. Casesnoves F (2019-20) Die numerische Reuleaux-Methode Rechnerische und dynamische Grundlagen mit Anwendungen (Erster Teil).
28. Ulmer W, Harder, D (1997) Corrected Tables of the Area Integral I(z) for the Triple Gaussian Pencil Beam Model. Z Med Phys 7(3): 192-193.
29. Ulmer W, Harder D (1995) A triple Gaussian pencil beam model for photon beam treatment planning. Med Phys 5(1): 25-30.
30. Ulmer W, Harder D (1996) Applications of a triple Gaussian pencil beam model for photon beam treatment planning. Med Phys 6(2): 68-74.
31. Ma C, Lomax T (2013) Proton and Carbon Ion Therapy. CRC Press.
32. Censor Y, Zenios S (1997) Parallel Optimization: Theory, Algorithms and Applications’. UOP.
33. Ulmer W, Pyyry J, Kaissl W (2005) A 3D photon superposition/ convolution algorithm and its foundation on results of Monte Carlo calculations. Phys Med Biol 50(8): 1767-1790.
34. Ulmer W, Harder D (1997) Applications of the triple Gaussian Photon Pencil Beam Model to irregular Fields, dynamical Collimators and circular Fields. Phys Med Biol 6: 68-74.
35. Haddad K, Anjak O, Yousef B (2019) Neutron and high energy photon fluence estimation in CLINAC using gold activation foils. Reports of practical oncology and radiotherapy 24(1): 41-46.
36. Sievinen J, Waldemar U, Kaissl W () AAA Photon Dose Calculation Model in Eclipse™. Varian Medical Systems Report. Rad #7170A.  
37. Vagena E, Stoulos S, Manolopoulou M (2016) GEANT4 Simulations on Medical LINAC operation at 18MV: experimental validation based on activation foils. Radiation Physics and Chemistry 120: 89-97.
38. Ethics for Researchers (2013) EU Commission. Directorate-General for Research and Innovation. Science in society/Capacities FP7.
39. Casesnoves F (1981) Surgical Pathology I course class notes and clinical practice of Surgical Pathology Madrid Clinical Hospital [ Professor Surgeon Dr Santiago Tamames Escobar ]. 4th academic year course for graduation in Medicine and Surgery. Lessons and practice Breast Cancer Surgical and Medical Treatment. 1980-1981. Madrid Complutense University 9(2).
40. Tamames Escobar S (2000) Cirugia/ Surgery: Aparato Digestivo. Aparato Circulatorio. Aparato Respiratorio/ Digestive System. Circulatory System. Respiratory System (Spanish Edition).
41. Formenti S, Sandra Demaria S (2013) Combining Radiotherapy and Cancer Immunotherapy: A Paradigm Shift Silvia C. Formenti, Sandra Demaria. J Natl Cancer Inst 105(4): 256-265.
42. Numrich R (2010) The computational energy spectrum of a program as it executes. Journal of Supercomputing 52: 119-134.
43. European Commission, Directorate-General for Research (2021) Unit L3. Governance and Ethics. European Research Area. Science and Society.
44. ALLEA (2017) The European Code of Conduct for Research Integrity, Revised Edn.; ALLEA: Berlin Barndenburg Academy of Sciences.
45. Good Research Practice (2017) Swedish Research Council.
46. Ulmer W, Schaffner B (2011) Foundation of an analytical proton beamlet model for inclusion in a general proton dose calculation system. Radiation Physics and Chemistry 80(3): 378-389.
47. Sharma S (2008) Beam Modification Devices in Radiotherapy. Lecture at Radiotherapy Department, PGIMER. India.
48. Barrett A, Colls (2009) Practical Radiotherapy Planning. Fourth Edition. Hodder Arnold.
49. Ahnesjö A, Saxner M, A Trepp (1992) A pencil beam model for photon dose calculations. Med Phys 19(2): 263- 273.
50. Brahime A (2000) Development of Radiation Therapy Optimization. Acta Oncologica 39(5): 579-595.
51. Bortfeld T, Hong T, Craft D, Carlsson F (2008) Multicriteria Optimization in Intensity-Modulated Radiation Therapy Treatment Planning for Locally Advanced Cancer of the Pancreatic Head. International Journal of Radiation Oncology and Biology Physics 72(4): 1208-1214.
52. Brown B, cols (2014) Clinician-led improvement in cancer care (CLICC) - testing a multifaceted implementation strategy to increase evidence-based prostate cancer care: phased randomised controlled trial - study protocol. Implementation Science 9: 64.
53. Bortifield T (2006) IMRT: a review and preview. Phys Med Biol 51(13): R363-R379.
54. Censor Y (1996) Mathematical Optimization for the Inverse problem of Intensity-Modulated Radiation Therapy. Laboratory Report, Department of Mathematics, University of Haifa, Israel.
55. Capizzello A, Tsekeris PG, Pakos EE, Papathanasopoulou V, Pitouli EJ (2006) ‘Adjuvant Chemo-Radiotherapy in Patients with Gastric Cancer. Indian Journal of Cancer 43(4): 174-179.
56. Tamer Dawod, EM Abdelrazek, Mostafa Elnaggar, Rehab Omar (2014) Dose Validation of Physical Wedged symmetric Fields in Artiste Linear Accelerator. International Journal of Medical Physics, Clinical Engineering and Radiation Oncology 3(4): 201-209.
57. Do SY, David A, Bush Jerry D Slater (2010) Comorbidity-Adjusted Survival in Early-Stage Lung Cancer Patients Treated with Hypofractioned Proton Therapy. Journal of Oncology 2010: 251208.
58. Ehrgott M, Burjony M (1999) Radiation Therapy Planning by Multicriteria Optimization. Department of Engineering Science. University of Auckland. New Zealand. Conference Paper.
59. Ezzel G (1996) Genetic and geometric optimization of three-dimensional radiation therapy treatment planning. Med Phys 23(3): 293- 305.
60. Effective Health Care (2008) Number 13. Comparative Efectiveness of Therapies for Clinically Localized Prostate cancer. Bookshelf ID: NBK554842.
61. Hansen P (1998) Rank-deficient and discrete ill-posed problems: numerical aspects of linear inversion’. SIAM monographs on mathematical modelling and computation.
62. Hashemiparast S, Fallahgoul H (2011) Modified Gauss quadrature for ill-posed integral transform. International Journal of Mathematics and Computation 13(11).
63. Isa N (2014) Evidence based radiation oncology with existing technology. Reports of practical oncology and radiotherapy 19(4): 259-266.
64. Johansson KA, Mattsson S, Brahme A, Turesson I (2003) Radiation Therapy Dose Delivery’. Acta Oncologica 42(2): 2003.
65. Khanna P, Blais N, Gaudreau PO, Corrales-Rodriguez L (2016) Immunotherapy Comes of Age in Lung Cancer, Clinical Lung Cancer 18(1): 13-22.
66. Kufer KH, Hamacher HW, Bortfeld T (2000) A multicriteria optimisation approach for inverse radiotherapy planning. University of Kaiserslautern, Germany.
67. Kirsch A (1996) An introduction to the Mathematical Theory of Inverse Problems. Springer Applied Mathematical Sciences 120.
68. Luenberger D (1989) Linear and Nonlinear Programming (2nd Edn.). Addison-Wesley.
69. Moczko, J, Roszak A (2006) Application of Mathematical Modeling in Survival Time Prediction for Females with Advanced Cervical cancer treated Radio-chemotherapy. Computational Methods in science and Technology 12(2): 143-147.
70. Ragaz, J, Ivo A Olivotto, John J Spinelli, Norman Phillips, Stewart M Jackson, et al. (2005) Regional Radiation Therapy in Patients with High-risk Breast Cancer Receiving Adjuvant Chemotherapy: 20-Year Results of the Columbia Randomized Trial’. Journal of National Cancer Institute 97(2): 116-126.
71. Steuer R (1986) Multiple Criteria Optimization: Theory, Computation and Application. Wiley.
72. Spirou SV, Chui CS (1998) A gradient inverse planning algorithm with dose-volume constraints. Med Phys 25(3): 321-323.
73. IJ Das, CW Cheng, DA Fein, B Fowble (1997) Patterns of dose variability in radiation prescription of breast cancer. Radiotherapy and Oncology 44(1): 83-89.
74. Casesnoves F (2018) Practical Radiotherapy TPO course and practice with Cyberknife. Robotic simulations for breathing movements during radiotherapy treatment. Sigulda Radiotherapy Cyberknife Center. Latvia. Riga National Health Oncology Hospital Varian LINACs TPO practice/lessons several Varian LINACs. Riga Technical University Bioengineering Training-Course Nonlinear Life 11(4).
75. Casesnoves F (2022) Radiotherapy Linear Quadratic Bio Model 3D Wedge Filter Dose Simulations for AAA Photon-Model [18 Mev, Z= 5,15 cm] with Mathematical Method System. Biomed J Sci & Tech Res 46(2): 2022.
76. Casesnoves F (1985) Master in Philosophy Thesis at Medical Physics Department. Protection of the Patient in Routinary Radiological Explorations. Experimental Low Energies RX Dosimetry. Medicine Faculty. Madrid Complutense University 51(2): 1984-1985.
77. Casesnoves F (1983-5) Ionization Chamber Low Energies Experimental Measurements for M-640 General Electric RX Tube with Radcheck ionization camera, Radcheck Beam Kilovoltimeter and TLD dosimeters. Radiology Department practice and measurements. Madrid Central Defense Hospital. Medical Physics Department. Master in Philosophy Thesis. Medicine Faculty. Complutense University. Madrid 11(4).
78. Casesnoves F (1985) Determination of Absorbed Doses in Routinary Radiological Explorations. Medical Physics Conference organized by Medical Physics Society Proceedings Printed. San Lorenzo del Escorial. Madrid.
79. Greening J (1985) Fundamentals of Radiation Dosimetry. Taylor and Francis. Second Edition.
80. International Commission of Radiation Protection (1977) Bulletin 26th. The International Commission on Radiological Protection. Recommendations of the International Commission on Radiological Protection. Pergamon Press. Copyright © 1977 The International Commission on Radiological Protection.
81. Stanton P, Colls (1996) Cell kinetics in vivo of human breast cancer. British Journal of Surgery 83(1): 98-102.
82. Hedman M, Bjork-Eriksson T, Brodin O, Toma-Dasu I (2013) Predictive value of modelled tumour control probability based on individual measurements of in vitro radiosensitivity and potential doubling time. Br J Radiol 86(1025): 20130015.
83. Fowler J (2010) 21 years of Biologically Effective Dose.The British Journal of Radiology 83(991): 554-568.
84. Loredana G. Marcu, Iuliana Toma-Dasu, Alexandru Dasu, Claes Mercke (2018) Radiotherapy and Clinical Radiobiology of Head and Neck Cancer. Series in Medical Physics and Biomedical Engineering. CRC Press.
85. Casesnoves F (2022) Radiotherapy 3D Isodose Simulations for Wedge Filter 18 Mev-Dose [ z = 5,15 cm ] with AAA Model with Breast Cancer Applications. International Journal on Research Methodologies in Physics and Chemistry (IJRPC) 9(2).
86. Garden A, Beadle B, Gunn G (2018) Radiotherapy for Head and Neck Cancers. Fifth Edition. Wolters Kluwer.
87. Casesnoves F (2023) Radiotherapy Genetic Algorithm Pareto-Multiobjective Optimization of Biological Efective Dose and Clonogens Models for Head and Neck Tumor Advanced Treatment. International Journal of Mathematics and Computer Research 11(1): 3156-3177.
88. Casesnoves F (2023) Radiotherapy effective clonogens model graphical optimization approaching linear quadratic method for head and neck tumors. International Journal of Molecular Biology and Biochemistry 5(1): 33-40.
89. Casesnoves F (2023) Training course Stereotactic Radiotherapy and Radiosurgery in Management of Metastatic Brain Tumors. Sigulda Stereotactic, Radiosurgery and Cyberknife Hospital. International Society of Radiosurgey. Sigulda, Latvia.
90. Joiner M, Kogel A (2019) Basic Clinical Radiobiology. CRC Press.
91. Cher M, Raz A (2002) Prostate Cancer: New Horizons in Research and Treatment. Kluwer Academic Publishers.
92. Sureka C, Armpilia C (2017) Radiation Biology for Medical Physicists. (Hardback). CRC Press.
93. Ramon J, Denis L (2007) Prostate Cancer. Springer-Verlag Berlin Heidelberg.
94. B Andisheh, M Edgren, Dž Belkić, P Mavroidis, A Brahme, BK Lind (2013) A Comparative Analysis of Radiobiological Models for Cell Surviving Fractions at High Doses. Technology in Cancer Research and Treatment 12(2): 183-192.
95. Casesnoves F (2018) Training work. Nonlinear Life Biomedical Training-Course. Riga Technical University and Riga Oncology Hospital.
96. Carini H, Fidock M, Van Gooland A (2019) Handbook of Biomarkers and Precision Medicine. CRC Press.
97. Joiner M, Kogel A (2019) Basic Clinical Radiobiology. CRC Press.
98. Casesnoves F (2023) Radiotherapy BED Model 2D Pareto- Multiobjective Evolutionary Optimization for Prostate Cancer Hyperfractionated Treatment. Biomed J Sci & Tech Res 51(2).
99. Chen A, Vijayakumar S (2011) Prostate Cancer. Radiation Medicine Rounds. Volune 2, Issue 1. Demos Medical.
100. Casesnoves F (2025) Research Based Book Chapter. 2D-3D-Numerical computational intelligence radiotherapy optimization for hyperfractionated radiation treatment planning with biological effective dose models.