Lakshmi N Sridhar*

doi:10.19080/CTBEB.2025.23.556109

Research Article

Bifurcation Analysis and Multiobjective Nonlinear Model Predictive Control of Drug Addiction Models

Lakshmi N Sridhar*

Department of Chemical Engineering, University of Puerto Rico, Mayaguez

Submission:October 07, 2024;Published:January 20, 2025

*Corresponding author:Lakshmi N Sridhar, Department of Chemical Engineering, University of Puerto Rico, Mayaguez

How to cite this article:Lakshmi N S. Bifurcation Analysis and Multiobjective Nonlinear Model Predictive Control of Drug Addiction Models. Curr Trends Biomedical Eng & Biosci. 2025; 23(2): 556109.DOI:10.19080/CTBEB.2024.23.556109

Abstract

Introduction

Bifurcation analysis and Nonlinear model predictive control were performed on drug addiction models. Rigorous proof showing the existence of bifurcation (branch) points is presented along with computational validation.

Materials and Methods

Bifurcation analysis was performed using the MATLAB software MATCONT while the multi-objective nonlinear model predictive control was performed by using the optimization language PYOMO.

Results

It is demonstrated (both numerically and analytically) that the presence of the branch points was instrumental in obtaining the Utopia solution when the multiobjective nonlinear model prediction calculations were performed.

Discussion

Branch points are singularities which are beneficial in obtaining optimal configurations without compromising other requirements.

Conclusions

Branch points leading to two separate branches were exhibited when bifurcation analysis was performed on the two drug addiction models considered in this paper. Rigorous analysis demonstrated that the presence of the branch points would result in the MNLMPC calculations..

Keywords: Drug; Addiction; Bifurcation; Optimal control

Introduction

Mental health has become a significant focus for researchers and medical doctors in the last decade. Ironically, drug addiction is both cause and effect for the existence of mental health problems. People with mental health issues resort to drugs and drugs in turn lead to mental health problems. Additionally, drug addiction has led to a considerable amount of poverty and crime. It is therefore important to develop strategies to curb drug addiction. The problem of drug addiction has led to computational research to develop reliable techniques to be able to control drug addiction. This work aims to perform bifurcation analysis in conjunction with multiobjective nonlinear model predictive control (MNLMPC) calculations on models involving drug addiction. This paper is organized as follows. First, the background section with the literature review is presented. The bifurcation analysis techniques and the multiobjective nonlinear model predictive control strategies are presented followed by a description of how the presence of singular points affects the MNLMPC calculations. Two drug addiction example problems where MNLMPC calculations are performed in conjunction with bifurcation analysis are presented. It is numerically demonstrated that the presence of bifurcation points in the drug addiction models enables the MNLMPC calculations to converge to the Utopia solution.

Background

Bae (2014) [1] studied the dynamics of tobacco addiction models. Mushayabasa, and co-workers (2011, 2015a, 2015b) [2-4] performed dynamic and optimal control studies of drug addiction models. Hasan et al (2013) [5] investigated the effect of having drug rehabilitation centers to combat drug addiction. Islam et al, (2017. 2020)[6] developed a mathematical analysis of some dynamic Models of drug addiction, while Lavi et al (2012) [7] studied the dynamics of drug resistance. Nyabadza et al (2013) and White et al (2007) [8,9] modeled the dynamics of crystal meth abuse and heroin epidemics. Rwat and co-workers (2024) [11] examined the effect of recycling the recovered individuals back into the population while Donoghoe (1996)[12] studied the effect of drugs on global health. Murray et al (2007) [13] studied the effect of cannabis on mental health Pluddemann, (2008) [14] investigated the use of strategies to monitor alcohol and substance abuse. Akanni et al (2021) Abidemi et al (2022) and Olaniyi et al (2023) [15-17] studied dynamic models involving illicit drug use.

All the optimal control work done so far involves single objective minimization. In this work, multiobjective

Nonlinear model predictive control calculations are performed on drug addiction models in conjunction with bifurcation analysis. It is numerically demonstrated for two problems involving drug addiction that the presence of bifurcation points enables the MNLMPC calculations to converge to the Utopia solution. The bifurcation analysis, the MNLPMC methods, and an explanation of why the presence of bifurcation points leads to the MNLMPC calculations converging to the Utopia solution are presented in an appendix at the end of this paper. This result is beneficial for developing strategies to minimize drug abuse while at the same time maximizing the number of individuals who do not take drugs. This is demonstrated in the first problem. In the second problem, it is shown that simultaneously minimizing the number of heavy and light drug users is as effective as the individual minimization of these two variables. The numerical results are now presented.

Results and Discussion

In this section, the results of bifurcation analysis and MNLMPC calculations for two problems involving drug addiction are presented. The models used are described in Islam et al (2020) and Mushayabasa et al (2015b)[]. The equations for each problem are presented followed by the bifurcation analysis and MNLMPC results.

Problem 1 Islam et al (2020) [] Equations representing Problem 1

• represents individuals who are not drug users, but at a high risk of taking drugs
• L(t) represents light drug users
• H(t) represents heavy drug users
• represents drug users under treatment in rehabilitation
• Q(t) represents individuals who will never take drugs

The equations are

The model parameters are

u₁,u₂,u₃ are the control variables where
• r represents the recruitment rate of the population
• μ is the natural mortality rate
• α is the interaction rate among the susceptible and light drug users
• β is the effective rate at which light users convert into heavy drug users
• δ the removal rate from addiction without treatment
• γ is the rate at which heavy addicts are being sent to rehabilitation for treatment
• u₁ is the awareness and educational programs
• u₂ is the family-based care
• u₃ represents the effectiveness of rehabilitation centers

Bifurcation analysis for Problem 1

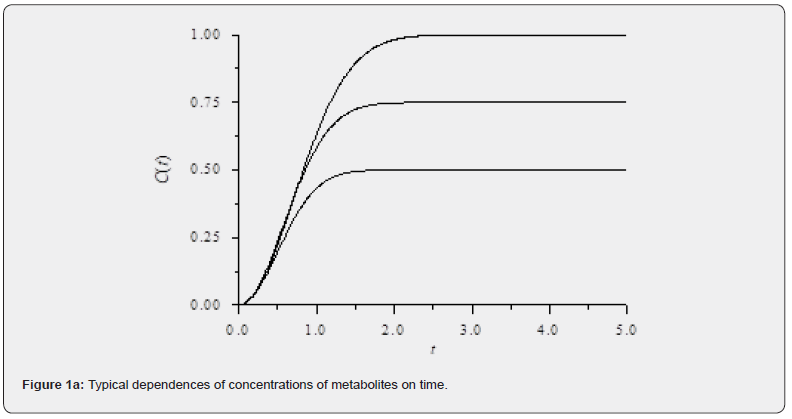
When bifurcation analysis with being the bifurcation parameter was performed on the equations representing problem 1, a branch point was found at values of (782.26, 0.0, 0, 0,0, 0.005433). Figure 1a shows the bifurcation diagram with this branch point.

MLNMPC for problem 1

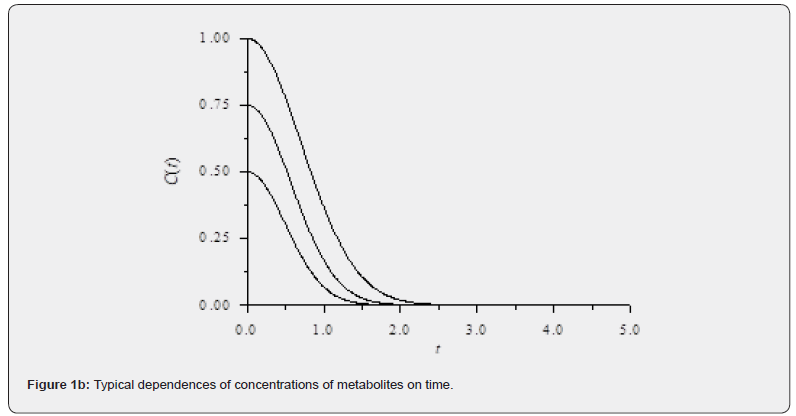
For the MNLMPC of problem 1, was maximized and resulted in a value of 2000; while was minimized and resulted in a value of 0. The multiobjective optimal control problem involved the minimization of subject to the dynamic equation set representing this problem. This resulted in the Utopia point of 0 and the MNLMPC values of the the control variables obtained were = [0.0004, 0.0405, 0.5362]. The MNLMPC profiles are shown in figures 1a-1i.

Problem 2 Mushayabasa et al (2015b) Equations representing Problem 2

In this problem, the time-dependent variables are
• S_v(t) susceptible individuals
• light or occasional drug users
• I_av(t) heavy drug users
• M_v(t) mentally ill population and (individuals who suffer mental illness due to drug use,
• R_v(t) detected illicit drug users

The equations that represent the drug addiction problem are

and the parameter values are
u_c,v_c are the control variables.
• α represents the rate at which light drug users become heavy drug users
• γ ,ε ,ρ the rates of detection and rehabilitation of individuals in classes
• σ ,φ the rates at which light and heavy illicit drug users develop mental illness
• ψ , d the permanent exit rates of light and heavy users
• δ mentally ill individuals who permanently exit the model because of death
• ω the rate at which individuals recover as a result of rehabilitation
• β the strength of interactions between susceptible individuals and illicit drug users
• u_c represents the reduction of the intensity of “social influence”
•v_c models the effort on the detection of illicit drug users

Bifurcation analysis for Problem 2

When bifurcation analysis with as the bifurcation parameter was performed on the equations representing problem 2, a branch point was found at = [ 1.0, 0.0, 0.0, 0.0, 0.0, 0.430112]. The bifurcation diagram is shown in Figure 2a.

MLNMPC for problem 2

For the MNLMPC of problem 2, ΣI_v(t) and ΣI_av( t) wereminimized individually and both the minimizations resulted in a value of 0. The multiobjective optimal control problem involved the minimization of subject to the dynamic equation set representing this problem. This resulted in the Utopia point of 0 and the MNLMPC values of the the control variables obtained were [u₁ ,u₂ ,u₃ ] = [0.0004, 0.0405, 0.5362]. The various MNLMPC profiles are shown in Figures 2b-2h. Two problems involving drug addiction models have been shown to exhibit branch points leading to two different solution branches. In both cases, it is computationally shown that the MNLMPC calculations would converge to the Utopia solution as the theoretical analysis predicts. These results demonstrate that the multiobjective nonlinear model predictive control strategy (MNPMPC) will obtain the best possible solution where 2 variables can be simultaneously optimized in drug abuse models. Hence the use of the MNMPC strategy will be very effective in minimizing the number of drug addictions.

Conclusions and future work

Branch points leading to two separate branches were exhibited when bifurcation analysis was performed on the two drug addiction models considered in this paper. Rigorous analysis demonstrated that the presence of the branch points would result in the MNLMPC calculations. This fact was also computationally validated. Future work would involve using drug addiction models with time delay.

Data Availability Statement

All data used is presented in the paper

Conflict of interest

The author, Dr. Lakshmi N Sridhar has no conflict of interest

Appendix (Details of MNLMPC and Bifurcation Analysis) Bifurcation analysis/

The existence of multiple steady-states (caused by limit and branch point singularities) and oscillatory behavior caused by Hopf bifurcation points) in chemical processes has led to a lot of computational work to explain the causes of these nonlinear phenomena.

MATCONT, (Dhooge and co-workers (2003,2004) [18,19] is a commonly used software to find limit points, branch points, and Hopf bifurcation points. Consider an ODE system

The tangent plane at any point x is

. Define matrix A given by

With the bifurcation parameter. The matrix A can be written in a compact form as

The tangent surface must satisfy

For both limit and branch points the matrix B must be singular. For a limit point (LP) the n+1^th component of the tangent vector v_n+1= 0 and for a branch point (BP) the matrix [A_v^T] must be singular., The function should be zero for a Hopf bifurcation point. indicates the bialternate product while I_n is the n-square identity matrix. A detailed derivation can be found in Kuznetsov (1998,2009) [20,21] and Govaerts (2000) [22]. Sridhar (2011) [23] used Matcont to perform bifurcation analysis on chemical engineering problems.

MNLMPC (Multiobjective Nonlinear Model predictive control) method

The multiobjective nonlinear model predictive control (MNLMPC) method was first proposed by Flores Tlacuahuaz et al (2012) [24] and used by Sridhar (2019) [25]. This method is rigorous, and it does not involve the use of weighting functions do not do it impose additional parameters or additional constraints on the problem unlike the weighted function or the epsilon correction method (Miettinen; (1999) [26]. For a problem that is posed as

The MNLMPC method first solves dynamic optimization problems independently minimizing/maximizing each x_i individually. The minimization/maximization of x_i will lead to the values x*_i . Then the optimization problem that will be solved is

This will provide the control values for various times. The first obtained control value is implemented and the remaining discarded. This procedure is repeated until the implemented and the first obtained control value are the same. The optimization package in Python, Pyomo (Hart et al (2017) [27] where the differential equations are automatically converted to a Nonlinear Program (NLP) using the orthogonal collocation method (Biegler, (2007) [28] is commonly used for these calculations. The state of the art solvers like IPOPT (Wachter and Biegler, (2006) and BARON (Tawaralmani and Sahinidis; (2005)[29,30] are normally used in conjunction with PYOMO.

Effect of singularities (Limit Point (LP) and Branch Point (BP)) on MNLMPC

Let the minimization be of the variables p₁ , p₂ l result in the values M₁ and M₂ . This The multiobjective objective function to be minimized will be

The Euler Lagrange equation (also known as costate equations will be

is the lagrangian multiplier. Taking the derivative of the objective function, we get

The co-state equation in optimal control is

λ_i is the lagrangian multiplier. The first term in this equation is 0 and hence

If the set of ODES has a limit or a branch point, is singular.

This implies that there are two different vectors-values for [λ_i] where and . In between there is a vector were. This coupled with the boundary condition λ_i(t_f =0 will lead to [λ_i]= 0 which will make the problem an unconstrained optimization problem. The only solution for the unconstrained problem is the Utopia solution.