Opinion

Metrology for 3D Quantitative Phase Imaging Instrumentation

Malgorzata Kujawinska* and Michal Ziemczonok

Institute of Micromechanics and Photonics, Warsaw University of Technology, Poland

Submission:December 12, 2023; Published:March 18, 2024

*Corresponding author:Institute of Micromechanics and Photonics, Warsaw University of Technology, 8 Sw. Andrzeja Boboli St., 02-252 Warsaw, Poland

How to cite this article:Malgorzata K, Michal Z. Metrology for 3D Quantitative Phase Imaging Instrumentation. Curr Trends Biomedical Eng & Biosci. 2024; 22(3): 556092. DOI:10.19080/CTBEB.2024.22.556092

Keywords:3D quantitative phase imaging; Biomedical applications; 3D refractive index; Metrology, Cell phantom; Digital twin; Two-photon polymerization; Anthropomorphic; Phantoms; Tomographic

Opinion

Three-dimensional quantitative phase imaging (3D QPI) delivers volumetric information about the refractive index (RI) distribution within microobjects and offers new solutions to outstanding challenges in cell biology and pathology [1-3]. Such imaging and measurement capabilities are of great interest to study the biophysical properties of biological microstructures such as single cells, cell aggregates, tissues or even small organisms, especially as they are complemented by high spatial resolution and label free sample preparation. Therefore, along with the development of multiplicity of research 3D QPI systems, the commercial devices using either spatial light interference (Phi Optics, Inc) or holographic tomography (TomoCube, Inc and NanoLive, Ltd) entered the market, readily tailored for microbiological applications. Despite of commercialization of these 3D QPI systems, their performance have not been fully quantified experimentally. The metrological and comparative stage is especially important in the case of techniques that intrinsically exhibit anisotropic spatial resolution i.e. all phase tomography techniques which capture data from a limited projection angle (LA) and therefore suffers so called “missing cone” problem [4]. Such architectures are most often used in biomedical applications. Quantitative 3D techniques have an additional layer of complexity - accuracy and uncertainty of the measurand - which in 3D is often intertwined with geometrical errors and there is no universal solution for their metrology. Additionally, due to the reliance on the diffraction of light, the reconstruction process involves solving heavily underdetermined inverse problem which allows numerous types of errors to appear in the reconstruction, often on a case-by-case basis [5]. Also one of the modern challenges in 3D QPI is to measure scattering samples with high resolution [6]. This is attributed to the facts that digital phase 3D histopathology requires investigation of tissue samples with increasing thickness, while complex biological structures, such as spheroids or organoids with significant scattering, tend to be more relevant models than 2D cell cultures e.g. for drug discovery. This demand stimulates the development of new methods [6,7], however it is difficult to select an appropriate one based on the scattering strength of the analysed sample [8]. Since, for all problems mentioned above there are no guidelines on how to report or address them, reconstruction errors related with them are often overlooked or just estimated, which undermines the confidence in the results.

For all these reasons it is necessary to introduce standardized methods for testing and reporting true metrological performance of 3D QPI systems. Current practise in 3D QPI is to selectively comment on major sources of errors, that are attributed to system parameters, acquired projections and reconstruction procedures (methods , approximations). This approach is relevant, but not sufficient to predict final reconstruction quality, as most of these components can be described qualitatively and error varies greatly depending on the particular method and features of interest. Ascertaining the reconstruction quality should be quantitative and practical, which requires suitable calibration objects and easily reproducible protocol.

Recent advancements in 3D nanoprinting, namely two-photon polymerization method TPP [9], have enabled development of a range of geometrical and anthropomorphic phantoms focused on recreating challenging aspects of real volumetric experiments. Fine-tuning the printing trajectory and the exposure dose allows simultaneous control over geometry and the refractive index in submicrometer and three-dimensional manner. The geometry and contrast of the 3D RI in the physical phantom proposed by Ziemczonok et al. [10] closely resembles real biological cells and recreates challenges related to their 3D reconstruction. In addition this cell phantom can be embedded inside a scattering cube made out of quasi-randomly distributed rods (see the first box in Fig.1). By adjusting the parameters of the scattering region (rod size, cube height, Ri contrast) or by adjusting the immersion liquid around the phantom it is possible to control the scattering strength [8]. The physical cell phantom can be measured using multiple reference techniques, most notably scanning electron microscopy, digital holographic microscopy and white light interferometry [10]. Based on the reference measurements, the numerical representation of the RI(x,y,z) of the cell phantom – its Digital Twin - is created. The phantoms’ parameters determined on its digital twin are considered ground truth for numerical simulations and reference values for experimental results (Figure1) [11].

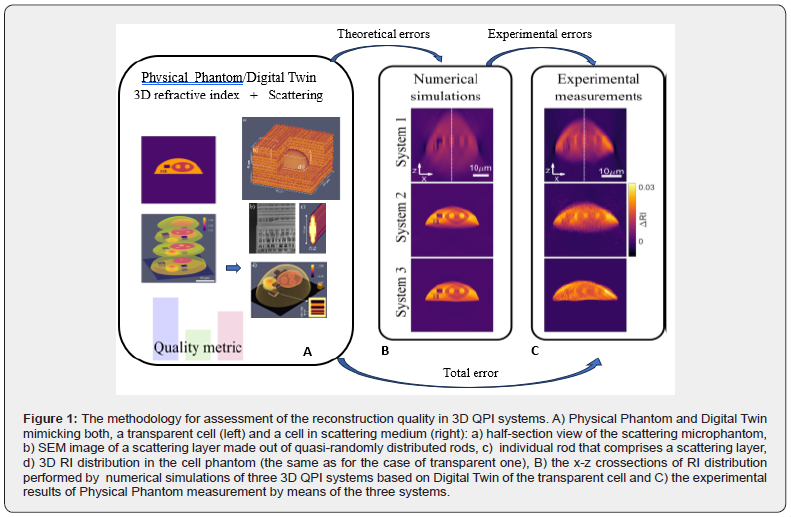
When reporting the result of measurement, it is obligatory to establish a quality metric, so the result reliability can be assessed [12]. The proposed metric consists of a range parameters related to cells’ physiology, that are often used to infer biomedical processes [11]. It includes both geometric/ volumetric features, as well as RI-related quantities which are reported in one of three ways: (1) RI is analyzed in the single 2D lateral slice only (similarly to the maximal intensity projection [13]), (2) RI is analyzed in the 3D segmented volume and (3) as dry mass, where RI is segmented in 3D and converted to dry mass using the refractive index increment that related dry mass density to the DRI value. In addition to the feature -based metric, two popular global metrics are considered: mean square error and structural similarity index. In practise, global quality metrics are widely used in 3D QPI, as they are usually objective and much easier to calculate and utilize. As a trade-off, however, they do not always correlate with the local RI accuracy and may mislead conclusions [11]. The methodology for assessment of the reconstruction quality using physical phantom, digital twin and the metrics explained above is schematically shown in Figure1. It can be implemented for a variety of QPI systems, type of a measured microobject (transmissive or scattering) and at arbitrary stage of QPI system development or final assessment of measurements. At the numerical simulation stage, the digital twin of the cell phantom is used in forward model in order to generate a set of projections – amplitude and phase maps. These projections are then used for investigation of tomographic reconstructions against four key parameters: regularization method, numerical aperture, number of projections and the object-immersion RI-contrast and finally the quantitative analysis of their contribution to different types of theoretical errors are evaluated. Knowing the theoretical errors calculated for the physical system parameters and the results of physical phantom measurements, the errors introduced by the experiment itself (including systematic errors introduced by hardware, the influence of the environmental conditions etc.) can be estimated and minimized. Finally the total error composed of the theoretical and experimental ones can be determined in the form of the quality metrics supported by the detail visualization in the form of selected 2D and 1D cross sections including comparison with the model and digital twin RI distribution.

Both developers and users of 3D QPI measurement devices benefit from the proper determination of accuracy and precision of instruments and uncertainty of measurements. The errors in the proposed methodology are quantified and the applicability of 3D QPI methods and systems for various measurement goals - from visualizing micrometre-scale features to full cell statistics – can be confirmed, providing reference point for past and future research. The proper metrology is crucial for cross-referencing a range of physical properties of cells, organoids and tissues with other laboratories and for further developments of biomedical applications in 3D QPI including remote diagnosis and drug discovery. Therefore the joint effort of the international metrology community and National Metrology Institutions (NMIs) together with the QPI instrumentation producers and users should be undertaken in order to agree on and disseminate the best practices for determination of accuracy, precision and uncertainty of 3D QPI systems, followed by introducing of standardized procedures. The proposed above phantoms and methodology may be considered as the first step in this important process.

References

1. Park Y, Depeursinge C, Popescu G (2018) Quantitative phase imaging in biomedicine, Nature Photonics 12(10): 578-589.
2. Balasubramani V, Kujawinska M, Allier C, Anand V, Cheng CJ, et al. (2021) Ziemczonok Roadmap on Digital Holography-Based Quantitative Phase Imaging. Journal of Imaging 7(12): 252.
3. Gul B, Ashraf S, Khan S, Nisar H, Ahmad I (2021) Cell refractive index: Models, insights, applications and future perspectives, Photodiagnosis and Photodynamic Therapy 33: 102096.
4. Balasubramani V, Kus A, Tu HY, Cheng CJ, Baczewska M, et al. (2021) Holographic tomography: techniques and biomedical applications [Invited], Applied Optics 60(10): B65.
5. Kus A, Krauze W, Makowski PL, Kujawinska M (2019) Holographic tomography: hardware and software solutions for 3D quantitative biomedical imaging, ETRI Journal 41(1): 61-72.
6. Yoon S, Kim M, Jang M, Choi Y, Choi W, et al., (2020) Deep optical imaging within complex scattering media. Nature Rev. Phys 2: 141-158
7. Rios AC, Clevers H (2018) Imaging organoids; A bright future ahead. Nature Methods 15: 24-26
8. Krauze W, Kuś A, Ziemczonok M, Haimowitz M, Chowdhury S, et al. (2022) 3D scattering microphantom sample to assess quantitative accuracy in tomographic phase microscopy techniques. Scientific Reports 12(19586): 1-9
9. Anscombe N (2010) Direct laser writing, Nature Photonics 4: 22-23
10. Ziemczonok M, Kus A, Wasylczyk P, Kujawinska M (2019) 3D-printed biological cell phantom for testing 3D quantitative phase imaging systems, Scientific Reports 9(1): 18872.
11. Ziemczonok M, Kus A, Kujawinska M (2022) Optical diffraction tomography meets metrology—Measurement accuracy on cellular and subcellular level, Measurement 195: 111106
12. JGGM 100: 2008 (GUM 1995 with minor corrections) evaluation of measurement data-guide to the expression of uncertainty of measurement, Joint Comm. Guides Metrol 19.
13. Fishman EK, Ney DR, Heath DG, Corl FM, Horton KM, et al. (2006) Volume rendering versus maximum intensity projection in CT angiography: What works best, when and why, RadioGraphics 26(3): 905-922