Review Article

Application of (Bio-) Chemical Engineering Concepts and Rules in Bioinformatics. Review of a CCM-Based Modular and Hybrid Kinetic Model Used to Simulate and Optimize a Bioreactor with Genetically Modified Cells

Gheorghe Maria^13*, Cristina Maria²and Laura Renea¹

¹1Department of Chemical and Biochemical Engineering, Politehnica University of Bucharest, Romania

²2National Institute for Research and Development in Environmental Protection, Bucharest, Romania

³Romanian Academy, Chemical Sciences Section, Romania

Submission: February 07, 2022; Published:February 21, 2022

*Corresponding author:Gheorghe Maria, Department of Chemical and Biochemical Engineering, Politehnica University of Bucharest, Polizu Str. 1-7, 011061, Bucharest, Romania

How to cite this article:Gheorghe Maria. Application of (Bio-) Chemical Engineering Concepts and Rules in Bioinformatics. Review of a CCM-Based Modular and Hybrid Kinetic Model Used to Simulate and Optimize a Bioreactor with Genetically Modified Cells. Curr Trends Biomedical Eng & Biosci. 2022; 20(3): 556039. DOI:10.19080/CTBEB.2022.20.556039

Abstract

This work briefly reviews the main concepts and principles used to solve difficult biochemical engineering, or bioengineering problems, by using extended structured cell kinetic models (including nano-scale state variables) linked in hybrid models to the biological reactor dynamic models (including macro-scale state variables). Exemplification is made for the case of the numerical methodology used by [Maria, 2021] to derive a structured hybrid modular kinetic model able to simulate the dynamics of a Fed-batch bioreactor (FBR), at both cell and bulk-phase species levels. The approached FBR includes a genetically modified E. coli culture used for the tryptophan (TRP) production. Eventually this complex hybrid dynamic model was used by [Maria and Renea, 2021] to derived the FBR optimal operating policy leading to the TRP production maximization.

Keywords: Biochemical engineering concepts; Principles and rules; Fed-batch bioreactor; Hybrid structured kinetic models; Tryptophan production

Introduction

As proved in the literature, the in-silico (math/kinetic model-based) numerical analysis of biochemical or biological processes are proved to be not only an essential but also an extremely beneficial tool for engineering evaluations aiming to determine the optimal operating policies of complex multi-enzymatic reactors [1-5], or bioreactors [6,7].

As reported over the last years, the use of structured cell models (based on the Central Carbon Metabolism - CCM) in the engineering evaluations “(to solve model-based design, optimization and control problems of industrial biological reactors) instead of the classical (default) unstructured models of Monod type (for cell culture bioreactors), or of Michaelis-Menten type (if only enzymatic reactions are retained) that ignores detailed representations of cell processes, presents a large number of advantages [8]. Thus, by accounting for only key process variables (biomass, substrate and product concentrations), these unstructured models do not properly reflect the metabolic changes, being unsuitable to accurately predict the cell response to environmental perturbations by means of (self-) regulation of the cell metabolism [9,10]. The alternative use of structured models (based on the cell reaction pathways), by accounting for cell metabolic reactions and component dynamics, leading to a considerable improvement in the predictive power, with the expense of incorporating a larger number of species mass balances with parameters difficult to be estimated from often incomplete data and, consequently, difficult to be used for industrial scale purposes. An alternative compromise is to use hybrid models that combine unstructured with structured process characteristics to generate more precise predictions [8]. Basically, hybrid models use a two-level hierarchy: the bioreactor macroscopic state variables linked with the nano-scale variables describing the cell metabolic processes of interest. Even if such a complex/extended model requires more experimental and computational efforts to be built-up, the resulted hybrid (bi-level) dynamic model presents a several advantages, as followings:

i. The extended model allows further in-silico (modelbased) engineering developments (bioreactor design, and its offline optimization) of a higher accuracy compared to unstructured models. For instance, the model could better predict the optimal time stepwise feeding policy of a Fed-batch reactor (FBR) to increase the Tryptophan (TRP) production (this paper example) [7,8].

ii. It can be used for bioinformatics purposes, by evaluating the influence of the bioreactor operating conditions (control macro-variables) on the dynamics of cell nano-scale keyintermediates and fluxes involved in the metabolite synthesis of interest (that is those belonging to glycolysis, ATP-recovery system, and TRP-operon expression in the present case), thus directing the design of genetically modified cells with desirable ‘motifs’ [8].

iii. It can be used to obtain lumped dynamic models for rapid engineering calculations, by employing specific model reduction rules and kinetic data valid in the local operating domains. See general models [11,12], or linear models [13,14]. Because of such an approach, the bioprocess complexity may be described by a succession of local reduced models enfolded on the real process. The local / reduced models include only some metabolic pathways to obtain relevant (of interest) process state predictions.

iv. The structured cell models are also useful for understanding the cellular bioprocess in direct connection to the bioreactor-operating mode. For instance, in such a way can be determined, by means of numerical techniques, conditions of occurrence of oscillations for the glycolysis [15], or oscillations in the TRP-operon expression [9,16], or those leading to a balanced cell growth (quasi-steady-state QSS, i.e. homeostasis) [17].

v. As proved in the present case study, such hybrid bilevel models allow more robust extrapolations of the bioprocess behaviour in the case of TRP production optimization in a FBR [7]. Some other case studies with using hybrid models to describe the dynamics of bioreactors and cell bioprocesses are given by: Maria and Luta to optimize the mercury uptake by modified E. coli cells in a FBR [10]; Maria et al. to optimize the succinate production by E. coli in a batch mode [18]; reviews of Maria [6]; Dorka on FBR optimization for the monoclonal antibodies (mAbs) production, etc. [6,19].

Generally, modelling the dynamics (and regulation) of the bacteria CCM is a subject of very high interest, allowing in silico design of modified cells with desirable characteristics of various applications in the biosynthesis industry, civil engineering, and other fields [20,21]. The interest for such a subject is even higher as long as most of the glycolysis intermediates are starting nodes for the internal production of lot of cell metabolites (e.g., amino-acids, succinate, citrate, etc. [16,18]). As documented by Maria, to overcome the cell process dynamics complexity, the metabolic pathway representation with continuous and/or stochastic variables remains the most adequate and preferred representation of cell processes, the adaptable-size and structure of the lumped model (species and/or reactions) depending on available information and the utilization scope [20,21].

As underlined by Maria, the main advantages of deterministic/ continuous variable kinetic models are coming from the use of experience, concepts, math representation, rules, and algorithms of the biochemical reaction engineering [20-22]. The reaction rate expressions in the deterministic models are the usual ones of biochemical reaction engineering that is of Michaelis-Menten or Hill type (see fig. 47 of Maria [21]). A large number of CCM kinetic models have been reported in the literature, such as those of [23-25]. A short discussion is given by Maria [8,26]. Such a CCMbased kinetic model (Figure 1) was used by to optimize a FBR [7,8]. In fact, the glycolysis together with the phosphotransferase (PTS)-system, or an equivalent one for GLC-uptake, and with the pentose-phosphate pathway (PPP), and the tricarboxylic acid cycle (TCA), all these are part of the so-called central carbon metabolism (CCM) (Figure 1)[18].

The parameters (rate constants) of deterministic dynamic models are estimated using the common (bio)chemical engineering rules of (Figures 2 & 3) [11,20,21], by using either dynamic (kinetic) data obtained in a chemostat under transient regime (e.g. pulse-like perturbations in the bioreactor influent [25], or using steady-state data (metabolites concentrations) obtained at homeostasis (i.e. balanced cell growth [20,27]), by solving the math model stationary algebraic set dCj/dt = 0 (where “j” indexes the cell species taken individually or lumped; C= species concentrations; t = time). Parameter estimate must fulfill physico-chemical meaning constraints related to metabolic reaction stoichiometry. Besides, the rate constants must be limited by the diffusional processes, and in agreement with the thermodynamic equilibrium steps. Additionally, due to the optimized metabolic cell process, when modelling individual Gene Expression Regulation (GERM), or Genetic Regulation Circuits (GRC) in living cells, under a whole-cell approach [20,27,28], cell models must fulfil some optimality constraints, that is: reaction rates must be maximal, but with rate constants limited by the diffusional processes; the total enzyme (proteine) content of the cell is limited by the isotonicity condition; also the total cell energy (ATP) and reducing agent (NADH) resources are limited; the reaction intermediate levels must be minimum; the cell model at homeostasis must be stable, that is will reach the steady-state after termination of a perturbation [29]; the keyspecies concentrations must be constant at homeostasis. Most of the mentioned aspects are discussed and exemplified by Maria [20,21,27,28,30].

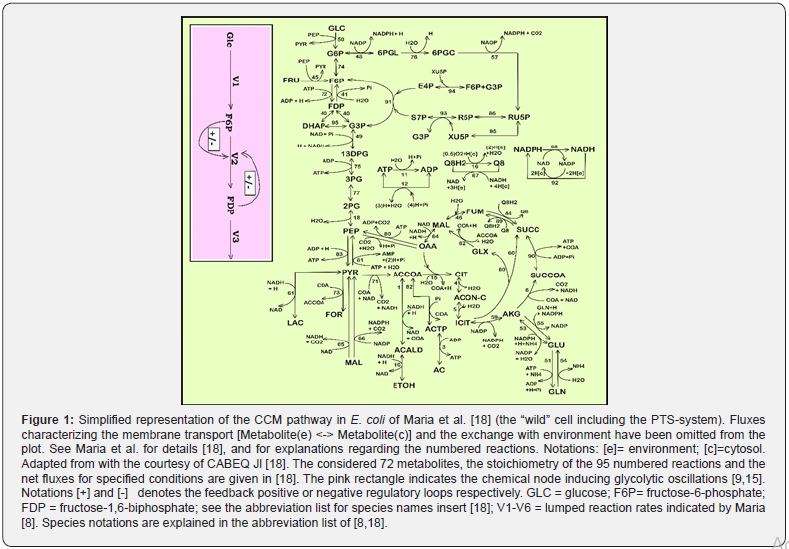
Even if complicated and, often over-parameterized, the continuous variable dynamic deterministic ODE (ordinary differential equations) models of the CCM metabolic pathways, or of GRC-s present a significant number of advantages, being able to reproduce in detail molecular interactions, the cell slow or fast continuous response to exo/ando-geneous continuous perturbations [31,32]. Besides, the use of ODE kinetic models presents the advantage of being computationally tractable, flexible, easily expandable, and suitable to be characterized using the tools of the nonlinear system theory [29], by accounting for the regulatory system properties, that is: dynamics, feedback / feedforward, and optimality. And, most important, such ODE kinetic modelling approach allows using the strong tools of the classical (bio-)chemical engineering modelling concepts summarized in (Figures 2 & 3). The most important ones are the followings [20,21,27,28]:

i. Molecular species conservation law (stoichiometry analysis; species differential mass balance set).

ii. atomic species conservation law ( atomic species mass balance).

iii. thermodynamic analysis of reactions (that is quantitative assignment of reaction directionality) [33].

iv. set equilibrium reactions; Gibbs free energy balance analysis; set cyclic reactions; find species at quasi-steady-state; improved evaluation of steady-state flux distributions that provide important information for metabolic engineering [34], allowing application of ODE model species and/or reaction lumping rules [11].

A discussion of the (bio-) chemical engineering concepts, principles, and tools is given by [35,36].

This paper is aiming to review the numerical methodology used by Maria and by Maria and Renea to derive a structured hybrid model able to simulate the dynamics of a FBR including a genetically modified E. coli culture used for the TRP production [7,8]. Eventually this complex modular structured and hybrid dynamic model was used to derive the optimal FBR operating policy leading to the TRP production maximization [7].

Short Review of a Case Study

The structured hybrid model

To exemplify a methodology to develop a structured CCMbased kinetic model linked to a classical macro-level dynamic model of a FBR, the case study of Maria was approached here [8].

The approached case study refers to the tryptophan (TRP) synthesis in modified E. coli cells (i.e. T5 strain of Chen et al. [37]). The required experimental data were collected from a labscale FBR by Chen [38]. The developed structured kinetic model includes several inter-connected reaction pathway (modules) able to simulate the dynamics of glycolysis, TRP-operon expression, ATP-recovery system, all belonging to the CCM. Experiments were carried out by using an E. coli strain (T5) modified to replace the PTS-system with a more efficient one to uptake the glucose (GLC) from the environment. By linking the FBR macroscopic state variables with the nano-scale variables describing the cell metabolic processes of interest, the resulted hybrid dynamic model presents a large number of advantages. Thus, the model allows further in-silico (model-based) more accurate engineering developments of practical interest for the biosynthesis industry related to TRP production maximization in a FBR using optimal feeding policies to be determined in a separate numerical analysis. Beside, such a hybrid structured model can be used for bioinformatics purposes, by evaluating the influence of the FBR operating conditions on the dynamics of key-intermediates involved in the cell (TRP) synthesis, thus directing the design of modified cells with desirable ‘motifs’ of practical interest

The metabolic flux analysis of Chen [38]; Chen [39]; Chen & Zeng [40] suggests that replacement of the wild PTS glucose uptake system with the galactose permease/glucokinase (galp/ glk) uptake system can theoretically double the TRP yield from glucose [38-40]. Finally, a promising strain T5 was obtained and fed-batch fermentations showed an increase of TRP specific production rate by 52.93% (25.3mg/gDW biomass /h) [37]. The cell flux analysis of Chen [39], and Chen [38] indicated the doubling of fluxes responsive with the TRP synthesis [7,38,39].

Basically, the structured CCM-based kinetic model of Maria includes four linked modules, that is (Figure 4-Left) [8]:

Module [X]: The biomass growth kinetic model (in the FBR bulk-phase). The rate constants of [X] module have been estimated by evaluating every time the biomass model with using the experimentally recorded species dynamic trajectories (i.e. X, and GLC here) instead of the required simulated data coming from the (missing at this stage) kinetic modules of (FBR-dynamics, and glycolysis).

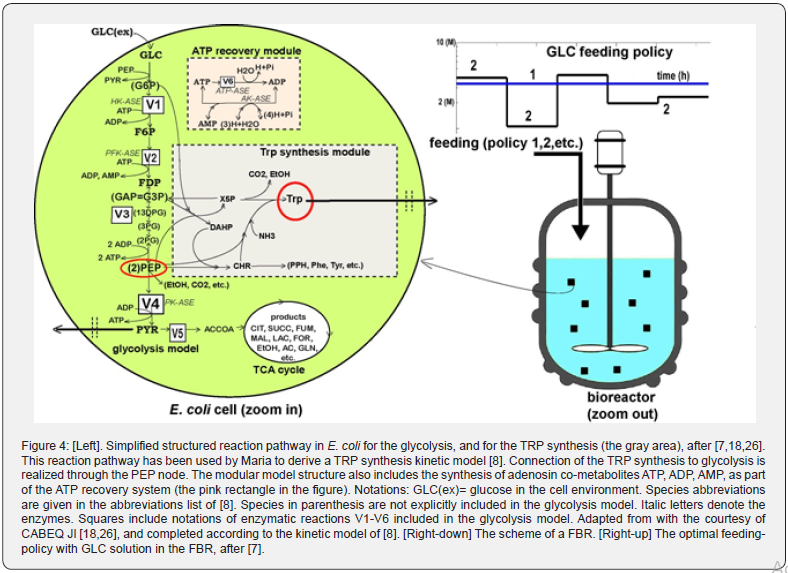
Module [a]: Glycolysis kinetic model (cell level). Starting from the extended reaction pathway of (Figure 1), and from the CCM model of Chassagnole et al. and of Maria et al. and by applying chemical engineering lumping techniques [18,25], Maria proposed a valuable reduced dynamic model of glycolysis (denoted by MGM) 26], by accounting only for 9 key-species in 7 lumped reactions, with including 17 easily identifiable rate constants belonging to V1-V6 metabolic fluxes (Figure 4-Left). The MGM rate constants have been identified by Maria with using the kinetic experimental kinetic data of Chassagnole et al. and Visser et al. obtained from FBR including a “wild” E.coli culture [25,26,41]. When using the modified E.coli in the FBR, Maria adjusted the MGM rate constants by using the GLC, (excreted) PYR, X experimental kinetic curves recorded over the FBR batch [8].

The MGM model has been proved to adequately reproduce the cell glycolysis under steady state, oscillatory, or transient conditions according to: i) the defined glucose concentration level/dynamics in the bioreactor, ii) the total A(MDT)P cell energy resources; iii) the cell phenotype characteristics (related to the activity of enzymes involved in the ATP utilization and recovery system) [9,15,16]. Here A(MDT)P denotes the lump of the following species: ATP = Adenosin-triphosphate; ADP = Adenosin-diphosphate; AMP = Adenosin-monophosphate. This is why, the FBR and the MGM glycolysis dynamic models are to be considered together when simulating the dynamics of the [GLC] in the FBR bulk-phase [8], and of the cell metabolites of interest {F6P(fructose-6-phosphate), FDP(fructose-1,6-biphosphate), PEP(phosphoenolpyruvate), PYR(Pyruvate), ATP} into the cell. The adopted rate expressions for the glycolysis main metabolic fluxes V1-V6 are those of the basic MGM model.

Module [b]: ATP recovery system (cell level, the pink rectangle in Figure 4). The adopted model for ATP-ADP-AMP dynamics (V6, and equilibrium relationships) in (Figure 4 - the pink square) imported from Maria was proved to fairly represent the dynamics and the thermodynamics of such an important internal module [9,26]. Rate constants were identified concomitantly with those of module [a], in the same way. As an observation, the two modules [a-b] are inter-connected by sharing the ATP species, while the module [a], and [X] are inter-connected by sharing {X, and GLC} species. Thus, the dynamics of species belonging to the three inter-connected modules {[a], [b], and [X]} can be simulated concomitantly, according to the reduced reaction pathway of (Figure 4).

Module [c]: TRP-synthesis (cell level, Figure 4). The kinetic models from the literature trying to reproduce the TRP-operon expression self-regulation are too extended for our purposes [42,43]. This is why, in the present analysis, simulations of the TRP synthesis were performed by using the reduced kinetic model of Maria et al. [9,16,17], and of Bhartiya et al. [44]. The rate constants estimation rule is repeated by also considering the module [c] of TRP-synthesis. First, one simulates the dynamics of this module individually, by using the rate constants and the reaction rate expressions from literature, as an initial guess. Because, the TRPmodule [c] includes the species (PEP) shared with the glycolysis module [a], simulations have been used the (PEP) time-trajectory transferred from the concomitant simulations of the (now available) three inter-connected modules {[a], [b], and [X]}. The necessary TRP time-trajectory was taken the experimental one (if necessary, interpolated with the cubic splines “INTERP1” facility of Matlab^™ package). Because the adopted TRP-inhibition model of Bhartiya et al. [44] does not fit properly the experimental data of Chen [38], another inhibition model has been proved to satisfactorily represent the experimental TRP data.

All the above described four kinetic model modules are integrated in the FBR dynamic model. To not complicate the numerical simulations, the FBR model adopted by Maria is a classical one [8], developed with the following main hypotheses: i) the operation is isothermal, iso-pH, and iso-DO; ii) it is selfunderstood that nutrients (that is, compounds playing roles of sources of carbon, nitrogen, and phosphorus) are added initially and during the FBR operation, in recommended quantities, and of an optimal C/N/P ratio [38], together with an excess of aeration for ensuring an optimally biomass maintenance, and any growth limitation due to such factors; iii) the volume of the perfectly mixed liquid phase (with no concentration gradients) increases according to the liquid feed flow-rate.

The use of the hybrid model to evaluate the modified E.coli strain efficiency

By using the structured hybrid model, Maria was able to simulate the (non-optimal) FBR performances when employing a “wild” E.coli culture, or a modified T5 strain [8]. The results indicated the superiority of the modified T5 E. coli strain in maximizing the TRP productivity under similar operating conditions, that is: i) a 100x higher flux (at the initial FBR conditions) of the imported GLC into the cell, leading to ca. 50% higher TRP-productivity of the FBR even if its operation is not the optimal one.

The use of the hybrid model to derive the optimal FBR operating policy

structured cell metabolic processes to the dynamics of macroscopic variables of the bioreactor, are more and more used in engineering evaluations to derive more precise predictions of the process dynamics under variable operating conditions. Depending on the cell model complexity, such a math tool can be used to evaluate the metabolic fluxes in relation to the bioreactor operating conditions, thus suggesting ways to genetically modify the microorganism purposes. Even if development of such an extended dynamic model requires more experimental and computational efforts, its use is advantageous [7].

The approached probative example refers to the four modules model described above successfully used to simulate the dynamics of some key-species from several pathways of the CCM of a modified E. coli cells, linked to the macroscopic state variables of a FBR used for the tryptophan (TRP) production. The used E. coli strain was modified to replace the PTS system for glucose (GLC) uptake with a more efficient one. In this chapter, one review the way by which Maria and Renea used this complex hybrid model to solve a difficult engineering problem [7], that is off-line determination of the optimal feeding policy of a FBR (Figure 4 [Right-down]). The difficulty of the optimization problem comes from several sources, that is: (i) the highly nonlinear hybrid model of the process-reactor; (ii) highly nonlinear constraints defining a non-convex domain; (iii) possible existence of multiple solutions of the optimization problem.

To solve this problem, (i) the batch time (48h. here) is divided in N_div “time-arcs” of equal lengths, and (ii) the control variables are kept constant only over every “time-arc” at optimal values for each time-arc determined from solving an optimization problem (i.e., maximization of the TRP production in this case). The time intervals of equal lengths Δt = t_f /N_div are obtained by dividing the batch time t_f into N_div parts t_j-1 ≤ t ≤ t_j, where t_j = jΔt are switching points (where the reactor input is continuous and differentiable). For the present case study, a value of N_div = 10 was adopted. A finer division of the batch time (that is for larger N_div) is not desirable because the necessary computational effort grows significantly (due to a considerable increase in the number of searching variables), thus hindering the quick (real-time) implementation of the derived FBR operating policy. Additionally, multiple optimal operating policies can exist for the resulting over-parameterized constrained optimization problem of a high nonlinearity, thus increasing the difficulty in quickly locating a feasible globally optimal solution of the FBR optimization problem. Additionally, as N_div increases, the derived operating policy is more difficult to implement, since the optimal feeding policy requires a larger number of stocks with feeding substrate solutions of different concentrations, separately prepared to be fed for every time-arc of the FBR operation (an overly expensive alternative) [7].

The chosen control variables are the followings:

a) The GLC substrate concentration in the feeding solution for every N_div time-arc.

b) The liquid feed flow rate for every N_div time-arc.

c) In total, there are N_div × 2 = 10 unknowns to be determined.

The objective function (Ω) used to solve the optimization problem must ensure maximization of the TRP production, that is:

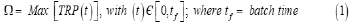
variables to be determined. By applying a very effective solver (that is the MMA algorithm of Maria [45]), the optimal time stepwise continuously feeding policy of the FBR was obtained (Figure 4 [Right-up]). As proved, this optimal FBR is able to increase the TRP production with 75% from which 50% is due to the used modified E. coli instead of the „wild” one, while 25% is coming from the time variable optimal feeding of the FBR.

Conclusion

The extended bi-level (hybrid) kinetic model reviewed in this paper was proven to adequately represent the dynamics of an experimentally studied FBR under a nominal (uniform feeding) operating policy, for both macroscopic state variables and for the cell key species of the CCM reaction modules related to the TRP production in the FBR, i.e. [a] glycolysis, [b] ATP recovery system, [c] TRP operon expression, and biomass [X] growth. The hybrid structured model, linking the macro state variables to the nano cell-scale variables, was validated using the recorded data from the lab-scale FBR over a long batch time (63h).

The paper exemplifies how the use of a moderate-size CCMbased hybrid kinetic model, of modular construction, including the inter-connected complex metabolic pathways of interest, is a continuously challenging subject when developing structured cell simulators for various engineering applications, such as (a) metabolic flux analysis under variable operating conditions; (b) target metabolite synthesis optimization by optimizing the bioreactor operation, and/or by modifying the cell strain; (c) in silico reprogramming of the cell metabolism to design GMOs (Genetically Modified Organisms); (d) a quick analysis of the cell metabolism, leading to an evaluation of substrate utilization, oscillation occurrence, and reactor Quasi-Steady- State (QSS) operating conditions, or structured interpretations of the metabolic changes in modified cells or in direct connection to the bioreactor operation mode; (e) bioreactor/bioprocess optimization (the present study); (f) to derive simple lumped models, locally valid (in the operating parameters domain); (g) to allow more robust extrapolations of the bioprocess behavior; (h) to determine operating conditions leading to minimization of the substrate consumption over the batch time, by keeping a high TRP-yield [7].

The use of the main concepts, principles, and rules of the (bio) chemical engineering were proved to be beneficial when developing extended structured cell kinetic models used to solve difficult biochemical engineering, or bioengineering problems [46].

References

1. Maria G (2012) Enzymatic reactor selection and derivation of the optimal operation policy, by using a model-based modular simulation platform. Comput Chem Eng 36: 325-341.
2. Maria G, Crisan M (2017) Operation of a mechanically agitated semi-continuous multi-enzymatic reactor by using the Pareto-optimal multiple front method. J Process Control 53: 95-105.
3. Maria G (2020) Model-based optimisation of a batch reactor with a coupled bi-enzymatic process for mannitol production. Comput Chem Engg 133: 106628-106635.
4. Maria G, Peptanaru IM (2021) Model-based optimization of mannitol production by using a sequence of batch reactors for a coupled bi-enzymatic process-A dynamic approach. Dynamics-Basel 1(1): 134-154.
5. Straathof AJ, Adlercreutz P (2005) Applied biocatalysis, Harwood Academic Publ Amsterdam, 2005.
6. Maria G (2020) Model-based optimization of a fed-batch bioreactor for mAb production using a hybridoma cell culture. Molecules-Basel 25(23): 5648-5674.
7. Maria G, Renea L (2021) Tryptophan production maximization in a fed-batch bioreactor with modified coli cells, by optimizing its operating policy based on an extended structured cell kinetic model. Bioengineering-Basel 8(12): 210-247.
8. Maria G (2021) A CCM-based modular and hybrid kinetic model to simulate the tryptophan synthesis in a fed-batch bioreactor using modified coli cells. Comput Chem Engg 153: 107450-107466.
9. Maria G (2020) In-silico determination of some conditions leading to glycolytic oscillations and their interference with some other processes in coli cells. Front Chem 8: 526679-526693.
10. Maria G, Luta I (2013) Structured cell simulator coupled with a fluidized bed bioreactor model to predict the adaptive mercury uptake by coli cells. Comput Chem Engg 58: 98-115.
11. Maria G (2004) A review of algorithms and trends in kinetic model identification for chemical and biochemical systems. Chem Biochem Engg Quarterly 18(3): 195-222.
12. Edwards K, Edgar TF, Manousiouthakis VI (1998) Kinetic model reduction using genetic algorithms. Comp Chem Engg 22(1-2): 239-246.
13. Martinez EC, Beltramini LJ (1990) Lumping upon time-scales: modeling upon topological factors. Chem Eng Sci 45(8): 2103-2108.
14. Maria G (2005) Relations between apparent and intrinsic kinetics of programmable drug release in human plasma. Chem Engg Sci 60(6): 1709-1723.
15. Maria G, Mihalachi M, Gijiu CL (2018) Model-based identification of some conditions leading to glycolytic oscillations in coli cells. Chem Biochem Engg Quarterly 32(4): 523-533.
16. Maria G, Gijiu, CL, Maria C, Tociu C (2018) Interference of the oscillating glycolysis with the oscillating tryptophan synthesis in the coli cells. Comp Chem Engg 108: 395-407.
17. Maria G, Mihalachi M, Gijiu CL (2018) In silico optimization of a bioreactor with an coli culture for tryptophan production by using a structured model coupling the oscillating glycolysis and tryptophan synthesis. Chem Eng Res Design 135: 207-221.
18. Maria G, Xu Z, Sun J (2011) Multi-objective MINLP optimization used to identify theoretical gene knockout strategies for coli cell. Chem Biochem Engg Quarterly 25: 403-424.
19. Dorka P (2007) Modelling batch and fed-batch mammalian cell cultures for optimizing MAb productivity. MSc diss University of Waterloo, Canada.
20. Maria G (2017) Deterministic modelling approach of metabolic processes in living cells-a still powerful tool for representing the metabolic process dynamics. Juniper Publishers Inc., USA, pp. 1-17.
21. Maria G (2018) In-silico design of Genetic Modified Micro-organisms (GMO) of industrial use, by using Systems Biology and (Bio) Chemical Engineering tools. Juniper Publishers Inc., USA, pp. 1-95.
22. Maria G (2017) Application of (bio) chemical engineering principles and lumping analysis in modelling the living systems. Curr Trends in Biomed Engg Bioscienc 1(4): 1-9.
23. Miskovic L, Tokic M, Fengos G, Hatzimanikatis V (2015) Rites of passage: requirements and standards for building kinetic models of metabolic phenotypes. Curr Opin Biotechnol 36: 146-153.
24. Kurata H, Sugimoto Y (2017) Improved kinetic model of Escherichia coli central carbon metabolism in batch and continuous cultures. J Biosci Bioeng 125(2): 251-257.
25. Chassagnole C, Noisommit Rizzi N, Schmid JW, Mauch K, Reuss M (2002) Dynamic modeling of the central carbon metabolism of Escherichia coli. Biotechnol Bioeng 79(1): 53-73.
26. Maria G (2014) In-silico derivation of a reduced kinetic model for stationary or oscillating glycolysis in Escherichia coli Chem Biochem Engg Quarterly 28(4): 509-529.
27. Maria G (2017) A review of some novel concepts applied to modular modelling of genetic regulatory circuits. Juniper Publishers Inc., USA, pp. 1-37.
28. Maria G, Gijiu CL, Maria C, Tociu C, Mihalachi M (2018) Importance of considering the isotonic system hypothesis when modelling the self-control of gene expression regulatory modules in living cells. Curr Trends Biomed Engg Bioscienc 12(2): 1-20.
29. Heinrich R, Schuster S (1996) The regulation of cellular systems. Springer, USA, pp. 1-138.
30. Maria G, Maria C, Tociu C (2017) Comments on two novel review ebooks in the area of deterministic modelling of metabolic processes and of genetic regulatory circuits in living cells. UPB Bull Sci Series B 79(3): 1-19.
31. Maria G (2005) Modular-based modelling of protein synthesis regulation. Chem Biocheml Engg Quarterly 19(3): 213-233.
32. Styczynski MP, Stephanopoulos G (2005) Overview of computational methods for the inference of gene regulatory networks. Comp Chem Eng 29: 519-534.
33. Haraldsdottir HS, Thiele I, Fleming RM (2012) Quantitative assignment of reaction directionality in a multicompartmental human metabolic reconstruction. Biophys J 102(8): 1703-1711.
34. Zhu Y, Song J, Xu Z, Sun J, Zhang Y, et al. (2013) Development of thermodynamic optimum searching (TOS) to improve the prediction accuracy of flux balance analysis. Biotechnol Bioeng 110(3): 914-923.
35. Woinaroschy A (2016) A paradigm-based evolution of chemical engineering. Chinese J Chem Engg 24(5): 553-557.
36. Gani R, Bałdyga J, Biscans B, Brunazzi E, Charpentier JC, et al. (2020) A multi-layered view of chemical and biochemical engineering. Chem Engg Res Design 155: A133-A145.
37. Minliang C, Chengwei M, Lin C, Zeng AP (2021) Integrated laboratory evolution and rational engineering of GalP/Glk-dependent Escherichia coli for higher yield and productivity of L-tryptophan biosynthesis. Metab Eng Commun 12: e00167.
38. Minliang C (2020) Novel approaches for in vivo evolution, screening and characterization of enzymes for metabolic engineering of Escherichia coli as hyper L-tryptophan producer. PhD thesis, TU Hamburg, pp. 1-156.
39. Chen L (2016) Rational metabolic engineering and systematic analysis of Escherichia coli for L-tryptophan bio production, PhD thesis, TU Hamburg.
40. Chen L, Zeng AP (2017) Rational design and metabolic analysis of Escherichia coli for effective production of L-tryptophan at high concentration. Appl Microbiol Biotechnol 101(2): 559-568.
41. Visser D, Schmid JW, Mauch K, Reuss M, Heijnen JJ (2004) Optimal re-design of primary metabolism in Escherichia coli using linlog kinetics. Metab Eng 6(4): 378-390.
42. Xiu ZL, Zeng AP, Deckwer WD (1997) Model analysis concerning the effects of growth rate and intracellular tryptophan level on the stability and dynamics of tryptophan biosynthesis in bacteria. J Biotechnol 58: 125-140.
43. Xiu ZL, Chang ZY, Zeng AP (2002) Nonlinear dynamics of regulation of bacterial trp operon: model analysis of integrated effects of repression, feedback inhibition, and attenuation. Biotechnol Prog 18(4): 686-693.
44. Bhartiya S, Chaudhary N, Venkatesh KV, Doyle FJ (2006) Multiple feedback loop design in the tryptophan regulatory network of coli suggests a paradigm for robust regulation of processes in series. J R Soc Interface 3(8): 383-391.
45. Maria G (2003) ARS combination with an evolutionary algorithm for solving MINLP optimization problems. In: Modelling, Identification and Control. IASTED/ACTA Press: Anaheim, CA, USA, pp. 112-117.
46. Shuler ML (1989) Chemical engineering problems in biotechnology. American Institute of Chemical Engineers, New York, USA.