Research Article

Ab Initio Analysis of Keratin (C6H12N2O4S2): A Density Functional Approach

Nirbhay Kumar Singh^1,2*

¹Department of Applied Physics, Krishna Engineering College, India

²Department of Physics, Krishna Public School International, India

Submission:January 19, 2022;Published:February 09, 2022

*Corresponding author:Nirbhay Kumar Singh, Department of Applied Physics, Krishna Engineering College, Bhilai (C.G) and Department of Physics, Krishna Public School International, Naya Raipur (C.G), India

How to cite this article: ANirbhay K S. Ab Initio Analysis of Keratin (C6H12N2O4S2): A Density Functional Approach. Curr Trends Biomedical Eng & Biosci. 2022; 20(3): 556037. DOI:10.19080/CTBEB.2022.20.556037

Abstract

Keratin is a protein constituting high-sulfur content and form the bulk of epidermal appendages such as hair, nails, claws, turtle scutes, horns, whale baleen, beaks, and feathers, it also help to regulate the size of cells, allow cells to move, grow, and divide heal wounds. It is also a building block of the human body and help in make-up of the tissues in the skin, hair, and nails. Keratin wastes mostly produced from the poultry farms, slaughterhouses, and leather industries. It is also dumped, buried, used for landfilling, or incinerated; all these actions increase the threats of environmental hazards, pollution, negatively influence the public health, and increase greenhouse gases concentration. Present paper is SIESTA based study on structural and physical properties of keratin by Density Function Theory (DFT). Here we use Molecular Electrostatic Potential (MEP) surface, Charge density analysis and Partial Density of State (PDoS) and Density of State types (DoS) analysis were performed to analyzed contribution of total energy states, and each atomic orbitals in molecules. Bond length, bond angle, molecular surface were analyzed by xcrysden and Jmol programme.

Keywords: Molecular electrostatics potential surface; Projected density of state; Density of states; Density function theory

Introduction

Keratin is a compound produce inside of cells and regenerative layer of skin and it is main component of mammal’s nails, hairs, hooves and outer layer of skin. It is a protective protein, which protect from scratching or tearing, it can be derived from the feathers, horns, and wool of different animals and used as an ingredient in hair cosmetics. Keratin treatment and supplements strength our hair and make it to look healthier [1,2]. Smoothness of hair depends on nature of thickness and types of keratin treatment. It is absorbed by hair cuticle of hair cell due to which it looks full and glossy. It can also make curly hair less frizzy, easier to style, and straighter in appearance. Since keratin is a protein, it is important to eat protein-rich foods i.e. Eggs, onion, salmon, sweet potato which produce keratin. Certain nutrients like sweet potatoes are high in vitamin A, sunflower seeds, mango, garlic, kale etc. help the body produce keratin and may help improve the health of the skin, hair, nails, and other tissues [3,4].

Here we use density function theory to investigate electronic structure, charge distribution, types of bond formation, bond length, bond strength, site of chemical reactivity, physical and chemical properties of Keratin [5]. This theory is based on calculation of behavior of materials and their properties on the basis of quantum mechanical considerations [6-8]. Number of states occupied by electron and forbidden energy gap between highly occupied molecular orbital (HOMO) in valence band and lowest unoccupied molecular orbital (LUMO) of conduction band determined by Density of States (DOS) using Spanish Initiative for Electronic Simulations with Thousands of Atoms (SIESTA) [9,10], a computer programing method used for electronic structure calculations and ab initio molecular dynamics simulations [11,12]. It uses atomic orbital as a basic set and Kohn-Sham self-consistent method in Local Density Approximations (LDA) and Generalized Gradient Approximations (GGA) [13]. Each atom acquire equilibrium positions by the forces per atom smaller than 0.01eV/Å. Molecular electrostatic potentials are calculated from partial charge data present in file by crystalline and molecular structure visualization program i.e. Xcrysden and Jmol. Jmol is useful if the set of orbitals is relatively small and if the user needs to display one at a time. It read data for a whole set of orbitals, and then calculate surfaces or contours for one or more of them. Xcrysden programme able to display crystalline structure, densities, isosurfaces, contours and able to possesses some tools for analysis of various properties.

Structural analysis of material predicted by Molecular Electrostatics Potential (MEP) surface. This surface able to predict molecules reactivity toward positive or negative charge reactants. It also represents total effect of electrostatic field produce by negative charge electrons in orbit and positive charge proton present in nucleus. Relative polarity of molecule due to total charge distribution with dipole moments, partial charges, electronegativity and site of chemical reactivity also analyzed by molecular electrostatics potential surface [14-17]. In present research we will study properties of keratin on the basis of DFT i.e. their conductivity, distribution of charges around different atoms, bond strength, bond length and site of reactivity. We will able to discuss the main cause of hair fall, hair structure, fingernail, skin, hooves and their protection. It is can be advise that the keratin can be extracted from hooves, wool, and feathers, can be used for supplements, treatments, and to help in their growth and strength.

Methodology

In this study we apply density-functional theory as in SIESTA which is abbreviation of a computational programming Spanish Initiative for Electronic Simulations with Thousands of Atoms [18]. Generalized Gradient Approximation (GGA) is used for determination of exchange and correlation potential [19]. The molecule is designed by an advanced molecule editor and visualizer designed platform use in computational chemistry called Avogadro. To obtain the exchange-correlation energy accurately norm-conserving pseudo potential and a Double- Zeta Polarized basis set (DZP) is used because they are capable of describing the scattering properties of an ion in a variety of atomic environments [20-23]. The electrons explicitly included in the calculations for each atom are the 1s¹ electron of hydrogen, 2s²2p² electrons (4 electrons) of carbon, 2s²2p>³ electrons (5 electrons) of nitrogen. 2s²2p⁴ electrons (6 electrons) of oxygen and 3s²3p⁴ electrons (6 electrons) of sulfur. The core electrons are replaced by the Projector Augmented Wave (PAW) and pseudopotential approach. Whole system is relaxed until the forces in all components of each atom are smaller than 0.01 eV/Å. The relaxed structures of polymer systems are given in Figure 1a & 1b.

Procedure of Optimization

For structural optimization we follow three step optimization processes i.e. mesh cut-off, k-points and lattice constant. Then by putting values obtain by above optimization process use of final optimizaiton of structure. In present experiment convergence test is performed in the range of 50 to 450Ry. The value of mesh cutoff which corresponds to the fineness of the real-space grid was found to be 200 Ry [24,25]. More the value of mesh cut-off shows finer real-space grid and better accuracy. In next step for the calculation of electronic structure of an infinite system directly and to take into account the effect of neighboring unit cells in periodic calculations we sample k-space in range of 2-12 and its value corresponds to lowest energy found to be 5. By the optimized values of mesh-cutoff and k-points; the cell size is optimized in the range of 6.0-12.0 Å. According to minimum energy, optimized values of cell size are 1.5 Å. Using above values we finally optimize the cell for structural characterization.

Result and Discussion

Structural optimization

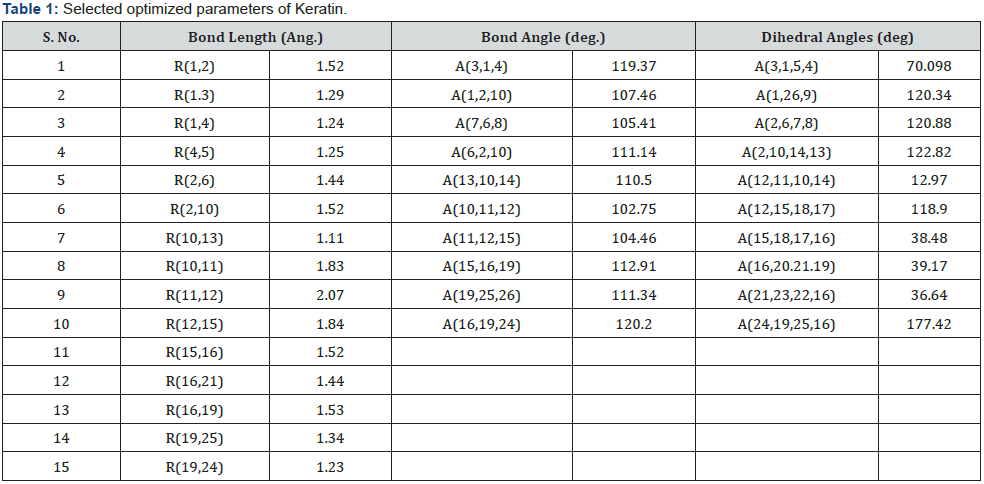
The optimized structure of keratin is shown in Figure 1a & 1b. Bond length of system affected by size of atom, orbital hybridization and electronic and steric behavior of atoms. In Keratin it is seen that all atoms are bounded by single bond it means all carbon atoms are sp³ hybdrized. Bond length, bond angle and dihedral angle between different atoms analyze by Jmol and Xcrysden represented in Table 1. Longer bond length between sulphur atoms represents that there is weaker attraction force between sulphur hence when keratin is stretched beyond a limit this bond will break and two mirror image structure of keratin is obtain. Each mirror image called Cysteine which contain sulfur-containing thiol (-SH) groups, where each sulfur atom bounded to other by cystine bond also known as disulfide bond which we draw as (-S-S-). Disilfide bond is quite stronger in nature but longer value of bond length as compare to other bond in keratin compound represent that it is comparatively weaker than other bond among other atom present here. This bond is also responsible for change the shape of hair from curly to straight.

Analysis of molecular electrostatic potential

Molecular Electrostatics Potential (MEP) method is more effective for analysis of various molecular properties, such as atomic charge distribution, electrostatic potential, hydrophobicity, polarizability, total charge distribution with dipole moment, electronegativity, partial charge distribution, site of chemical reactivity of a molecules and interaction of one molecules with another [26,27]. It also provides a visual method to understand the relative polarity of a molecule from which we can easily explain nature of hydrogen bonding, reactivity and structural relationship of molecules.

The projections of Molecular Electrostatics Potential (MESP) of keratin using Xcrysden and Jmol are given in Figure 2a-2d. Molecular surface around keratin using Xcrysded and Jmol represented in Figure 2a & 2b. Different color on the surface of molecule corresponds to different values of electrostatic potential. Most negative potential surface around oxygen are shown by red color and most electropositive electrostatics potential around hydrogen are represented by blue color represents, the molecular surface which having moderate value around sulfur are shown by yellow color and the zero potential surface around carbon shown by green colour [28-30]. Thus proton having affinity toward red colour surface and negative charge species having affinity toward blue color surface. Figure 2c is Van der Waal’s surface represented by ball and stick model, here sulfur (yellow), hydrogen (white) and oxygen is red it shows that total electron density around keratin is uniform distributed which also confirm by molecular electrostatics surface represent by Figure 2d [31-34].

Analysis of charge density

The XSF file obtains by SIESTA output use to analyze nature of chemical bonds and molecular surface by charge density analysis using Xcrysden. Figure 3a-3d shows charge density distribution of keratin at different resolutions [35,36]. It is observed from the figure that there is overlapping of charge density around C-C and C-H bond which indicate are covalent bond formation, while separation of charge density in C-O bond indicate that it is partially convent and partially ionic but charge around S-S bond are circularly distributed and isolated shows ionic nature which leads to localized wave functions shown by concentric spheres centered at atoms with a smaller degree of overlap. The charge density distributions in the systems are higher in the inner-most region (magenta), and lower in the outer most regions (red). Higher charge density around oxygen and sulphur is due to higher value of ionization energy or electronegativity than other atoms present in compound. The concentric circle around oxygen and sulphur atoms represents ionic bond while distortion in circles between carbon and oxygen is an indication of a partial covalent and partial ionics. The overlaping lobe between carbon nitrogen represent the bond is covalent.

Analysis of DoS and PDoS

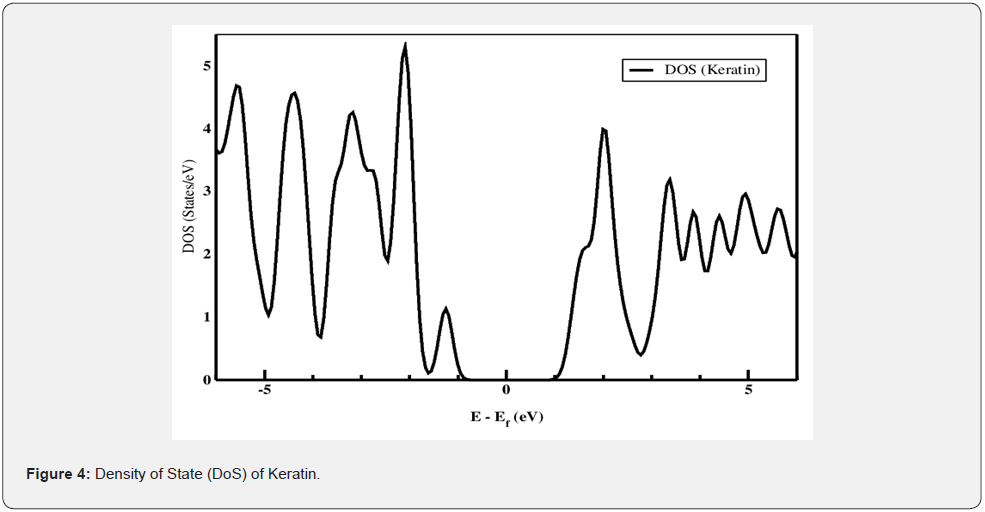
Density of States (DoS) represents number of different states at a particular energy level that are occupied by electrons in molecule. Relative contribution of a particular orbital of an atom in DOS analyzed by projected or partial density of states (PDoS) [37,38]. It also provides qualitative analysis of the electronic structure of material. Figure 4 & 5 represent experimental outcome of Density States (DOS) of and Projected Density of States (PDOS) of different atoms of keratin obtain by Siesta output are analyzed by Xmgrace programme.

From density of states analysis as shown in Figure 4 we can calculate contribution of frontier molecular orbitals i.e Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO) in chemical composition. The HOMO is the outermost (highest energy) orbital containing electrons that could act as an electron donor while LUMO is the innermost (lowest energy) orbital that has room to accept electrons and can act as the electron acceptor. It shows that the Highest Occupied Orbitals (HOMO) of one molecule and the Lowest Unoccupied Orbitals (LUMO) of the other interact with each other causing attraction [39-41]. The energy value corresponding to HOMO and LUMO are found to be -1.24 eV and 1.56 eV respectively, thus forbidden energy gap between valence and conduction band is about 3.8 eV which shows keratin is electrically insulator in nature. Below HOMO at energy level -3.2 eV and -4.20 eV some more peak are obtain which represent valence band completely filled by electron of different atoms similarly above HOMO the peaks represent electrons of atoms present in conduction band.

Contribution of different atoms in conduction band, valence band analyzed by Partial Density of States (PDOS), which is shown in Figure 5. This figure represent that wave function of 2p orbitals of C, O, N and S and 2s orbital of N and O corresponding to energy valued 1.24 eV overlap and form Lowest Unoccupied Molecular Orbital (LUMO). Highest Occupied Molecular Orbital (HOMO) form by overlapping of 2p orbital of N and O and 2s orbital of oxygen at energy level 1.56 eV. It is also seen that in conduction band electrons of H (1s orbital) and O (2p orbital) play main role but in valence band electrons of C (2p orbital) and N (2p orbital) electrons are primary contributors.

Conclusion

From overall analysis it is concluded that Keratin is capable to recover and/or improve the mechanical properties of hair. It is present in our skin, hair, and nails where they help to make these tissues strong and flexible. From DFT analysis of keratin it is concluded that larger value of band gap between HOMO and LUMO (3.8 eV) corresponds to insulating nature i.e. it is bad conductor of heat and electricity. Molecular surface analysis shows that there is no active site thus due to insulating nature and lacking of active site keratin protects our hair, skin and nails to react from outer atmospheric contamination or pollutant. Ionic nature of bond and longest bond length between S-S atoms shows that there is weak attraction between them. Thus this bond is mainly contributed in smoothness and curling nature of hair. Finally it can be seen that S-S bond play main role in keratin for their strength. Thus for stronger and healthy hair S-S bond must be protected therefore for the strength of keratinocyte protein it should be advice to use sulfur rich oil or food which can be obtain from animal and plant based protein as well as other types of compounds such as sulfates, allicin, and sulfides, thiamin (vitamin B-1) and biotin (vitamin H). This paper is helpful for further study for the researcher working in the field of bioengineering and diseases or problems related to the hair and scalp, as well as their treatments.

Acknowledgment

Authors are grateful to Dr. M L Verma (HOD, SSGI Bhilai), Dr. B Keshev Rao (Professor SSGI, Bhilai) and to the management of Shri Shankaracharya Technical Campus-SSGI for providing lab facility to their campus and special guidance to lean SIESTA. I also thank to Mr. Anand Tripathi (Chairman KEC, Bhilai), Mr. Abhishek Tripathi (Director KPSI, Raipur), Ms. Vinita Mairal (Principal KPSI Raipur) and Ms. Sumangla Sundri (Vice Principal KPSI Raipur) for providing overall support to complete this research work.

References

1. Acda MN (2010) Waste chicken feather as reinforcement in cement-bonded composites. Philippine J Sci 139(2): 161-166.
2. Agrahari S, Wadhwa N (2010) Degradation of chicken feather a poultry waste product by keratinolytic bacteria isolated from dumping site at Ghazipur poultry processing plant. Int J Poult Sci 9(5): 482-489.
3. Alsarra IA (2009) Chitosan topical gel formulation in the management of burn wounds. Int J Biol Macromol 45(1): 16-21.
4. Aluigi A, Sotgiu G, Ferroni C, Duchi S, Lucarelli E, et al. (2016) Chlorin e6 keratin nanoparticles for photodynamic anticancer therapy. RSC Adv 6(40): 33910-33918.
5. Soler MJ, Artacho E, Gale JD, Garcia A, Junquera J, et al. (2002) The SIESTA method for ab Initio Order-N materials simulation. J Phy: Condens Matt 14(11): 2745-2779.
6. Bassani F, Liedl GL, Wyder P (2005) Encyclopedia of Condensed Matter Physics Reference Work. Academic Press, pp. 1-76.
7. Michael V, Hartmut L , Raphael W (2020) Classical dynamical density functional theory: from fundamentals applications. Adv in Phy 69 (2): 121-247.
8. Evans R, Oettel M, Roth R, Kahl G (2016) New developments in classical density functional theory. J Phy: Condens Matt 28(1-6): 240401.
9. Martin RM (2004) Electronic structure: basic theory and practical methods. Cambridge University Press.
10. Artacho E, Sanchez Portal D, Ordejon P, Garcia A, Soler JM (1999) Linear-scaling ab-initio calculations for large and complex system. Phys Stat Sol (b) 215(1): 809-817.
11. Ordejon P, Artacho E, Soler JM (1996) Self-consistent order-N density-functional calculations for very large systems. Phys Rev B Condens Matter 53(16): 10441-10444.
12. Kang HT, Hwang ES (2006) 2-Deoxyglucose: an anticancer and antiviral therapeutic, but not any more a low glucose mimetic. Life Sci 78(12): 1392-1399.
13. Bharatam PV, Patel DS, Iqbal P (2005) Pharmacophoric features of biguanide Derivatives: an electronic structure study. J Med Chem 48(24): 7615-7622.
14. Bharatam PV, Sundriyal S (2006) Molecular electrostatic potentials in the design of dendrimers for the delivery of glitazones. J Nanosci Nanotechnol 6(9-10): 3277-3282.
15. Roy DK, Balanarayan P, Gadre SR (2009) Signatures of molecular recognition from the topography of electrostatic potential. J Chem Sci 121: 815-821.
16. Rastelli G, Pacchioni S, Sirawaraporn W, Sirawaraporn R, Parenti MD, et al. (2003) Docking and database screening reveal new classes of Plasmodium falciparum dihydrofolate reductase inhibitors. J Med Chem 46(14): 2834-2845.
17. Cankurtaran BO, Gale JD, Ford MJ (2008) First principles calculations using density matrix divide-and-conquer within the SIESTA methodology. J Phy: Condens Matt 20(29): 1-12.
18. Jaffe JE, Snyder JA, Lin Z , Hess AC (2000) LDA and GGA calculations for high-pressure phase transitions in ZnO and MgO. Phys Rev B 62: 1660.
19. Perdew JP, Burke K, Ernzerhof M (1997) Generalized gradient approximation made simple. Phys Rev Lett 77: 3865.
20. Trouillier N, Martins JL (1991) Efficient pseudopotentials for plane-wave calculations. Phys Rev B Condens Matter 43(3): 1993-2006.
21. Shen C, Wang J, Tang Z, Wang H, Lian H, et al. (2009) Physicochemical properties of poly(ethylene oxide)-based composite polymer electrolytes with a silane-modified mesoporous silica SBA-15. Electrochim Acta 54(12): 3490-3494.
22. Hohenberg P, Kohn W (1964) Inhomogeneous electron gas. Phy Rev 136(3B): 864.
23. Joshi BD, Chaudhary PN (2013) Molecular Structure MESP, HOMO-LUMO and vibrational analysis of β-asarone using density functional theory. Kathmandu Univ J Sci Engg Tech 9(2): 1-14.
24. Joshi BD, Srivastava A, Gupta V, Tandon P, Jain S (2013) Spectroscopic and quantum chemical study of an alkaloid aristolochic acid I. Spectrochim. Acta A Mol Biomol Spectrosc 116: 258-269.
25. Politzer P, Truhlar DG (1981) Chemical applications of atomic and molecular electrostatic potentials, reactivity, structure, scattering, and energetics of organic, inorganic, and biological systems. Springer, p. 472.
26. Pingale SS (2011) Molecular electrostatic potentials concepts and applications. Phys Chem 13: 15158.
27. Politzer P, Grice ME, Murray JS, Seminario JM (1993) Anomalous stabilizing and destabilizing effects in some cyclic π-electron systems. Can J Chem 71: 1123-1127.
28. Suresh CH, Alexander P, Vijayalakshmi KP, Sajith PK, Gadre SR (2008) Use of molecular electrostatic potential for quantitative assessment of inductive effect. Phys Chem Chem Phy 10(43): 6492-6499.
29. Balnarayan P, Gadre SR (2003) Topography of molecular scalar fields. I. Algorithm and Poincare-Hopf relation. J Chem Phys 119(10): 5037.
30. Rocha AR, Garcia Suarez VM, Bailey SW, Lambert CJ, Ferrer J, et al. (2005) Towards molecular spintronics. Nat Mater 4(4): 335-339.
31. Huzinaga S, Andzelm J, Radzio Andzelm E, Sakai Y, Tatewaki H, et al. (1984) Gaussian basis sets for molecular calculations. In: Huzinaga S (Ed.), Physical science data, Elsevier B.V, USA, 16: 1-426.
32. Jollet F, Torrent M, Holzwarth N (2014) Generation of projector augmented-wave atomic data: A 71 element validated table in the XML format. Computer Phys Commun 185: 1246-1254.
33. Kuehman CJ, Olson GB (2009) Computational materials design and engineering. Material Sci Technol 25(4): 472-478.
34. Panchal JH, Kalidindi SR, Mc Dowell DL (2013) Key computational modeling issues in integrated computational materials engineering. Computer-Aided Design 45(1): 4-25.
35. Verma OP, Meshram MR, Mishra AK, Verma ML, Rao BK (2020) Structural electronic and optical properties of In₂O₃: a density functional study. Optical Quant Electronics 52(5).
36. Verma ML (2019) Structure and properties of biopolymer chitosan: a first principle study. I- manager’s J Mat Sci 7(3): 19-32.
37. Rangel T, Rignanese GM, Olevano V (2015) Can molecular projected density of states (PDoS) be systematically used in electronic conductance analysis. Beilstein J Nanotechnol 6: 1247-1259.
38. Kaliginedi V, Moreno Garcia P, Valkenier H, Hong W, García Suárez VM, et al. (2012) Correlations between molecular structure and single-junction conductance: a case study with Oligo(phenylene-ethynylene)-Type Wires. J Am Chem Soc 134(11): 5262-5275.
39. Perrin ML, Frisenda R, Koole M, Seldenthuis JS, Celis Gil JA, et al. (2014) Large negative differential conductance in single-molecule break junctions. Nat Nanotechnol 9(10): 830-834.
40. Strange M, Thygesen KS (2011) Towards quantitative accuracy in first principle transport calculations: The GW method applied to alkane/gold junctions. Beilstein J Nanotechnol 2: 746-754.
41. Ning J, Li R, Shen X, Qian Z, Hou S, et al. (2007) First-principles calculation on the zero-bias conductance of a gold/1,4-diaminobenzene/gold molecular junction. Nanotechnol 18: 345203.