Xi Wei, Pinjing Wen and Yuan Lin

doi:10.19080/CTBEB.2019.19.556005

Mini Review

Continuum-Level Simulations of Biopolymer Networks: A Minireview

Xi Wei, Pinjing Wen and Yuan Lin*

Department of Mechanical Engineering, The University of Hong Kong, China

Submission: March 19, 2019; Published: April 18, 2019

*Corresponding author: Yuan Lin, Department of Mechanical Engineering, The University of Hong Kong, Hong Kong, China

How to cite this article: Xi W, Pinjing W, Yuan L. Continuum-Level Simulations of Biopolymer Networks: A Minireview. Curr Trends Biomedical Eng & Biosci. 2019; 19(1): 556005. DOI: 10.19080/CTBEB.2019.19.556005

Abstract

The mechanical properties of living cells are governed by the cytoskeleton, a network consisting of many different biopolymers together with transient linker proteins [1]. Biopolymers, especially those composed of globular proteins, are known to be semiflexible, that is the persistence length of these filaments is often comparable to their contour length, leading to small, yet significant, thermal fluctuations around a straight conformation and ultimately resulting in mechanical properties far from those exhibited by synthetic materials made of highly flexible polymers [2]. Theoretically, it remains a great challenge to understand/predict how a semiflexible filament network behave because of its many-body nature as well as the coupled elastic and entropic effects involved. For this reason, there has been a growing interest in the direct simulation on computer-generated networks in recent years. Here, we briefly review various continuum-level simulation approaches that have been developed in the past few decades.

Mini Review

Mikado model

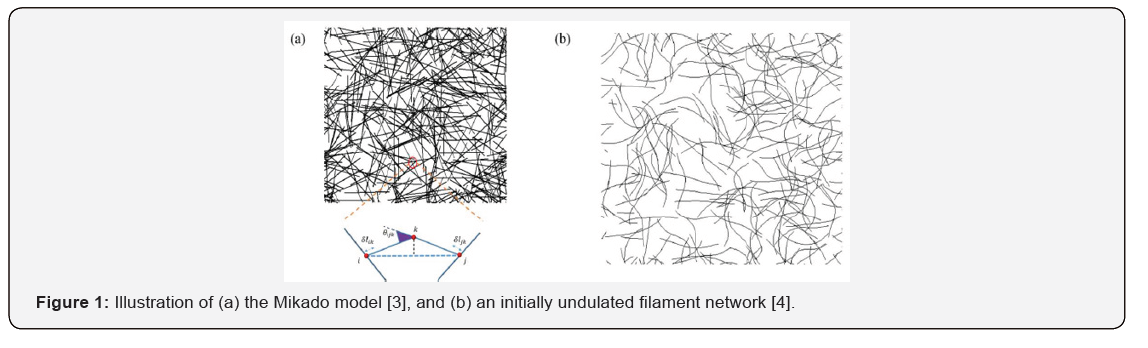
One of the simplest methods for analyzing the response of a biopolymer network is the Mikado model [2,3]. Basically, a Mikado network is constructed by randomly depositing certain number of filaments of length l inside a two-dimensional square of size w*w and with periodic boundary condition, as shown in Figure 1(a). Different filaments are assumed to be permanently cross-linked together at intersection points between them. Under such circumstance, the strain energy stored in the system is expressed as

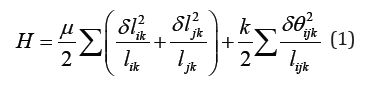
in which i and j correspond to two intersecting points while krepresents the midpoint between them. ikl and jkl stand for the length of segment ik and ,jk respectively, with glik and gljk being their elongation. ()12ijkikjklll=+ is the average length of the two segments and ijkδθ represents the angle change between segment ik and .jk Essentially, this model treats the filaments as elastic rods with respect to stretching and bending, withμandkrepresenting the corresponding stretching and bending stiffness. Interestingly, simulations from such an approach revealed that the network deformation is non-affine at small strains due to significant bending of individual biopolymers.

Combined FEM-Langevin dynamics approach

It is worthy to point out that thermal fluctuations of semiflexible biopolymers have not really been captured in the aforementioned continuum level simulations. The only attempt to address this was made by Onck et al. [4] and Huisman et al. [6], where an undulated shape (Figure 1 b) was assigned to each filament only at the beginning to account for the thermal excitations. Nevertheless, such treatment is not very realistic as filaments should undergo fluctuations dynamically and continuously. To solve this issue, Lin et al. [11] developed a Langevin dynamics-based formulation to describe the shape undulations of biopolymers. In particular, according to Langevin [12], the effect of collisions of medium molecules on the biofilament can be represented by two terms: a viscous force ςV acting on the biopolymer with ζ being the viscous coefficient per unit length and V corresponding to the local velocity of the moving biopolymer; and a random force f distributed along the filament (Figure 2a). This formulation was then implemented in the FEM simulations [11], where the transverse load 1 , j j t t+   as shown in Figure 2 a, was generated randomly from a Gaussian distribution with zero mean and a variance of 2 , B ζ kT ΔxΔt with Δx and Δt being the element length and the size of the time step, respectively. Using this method, simulations showed that the response of randomly cross-linked Factin networks undergoes transitions from being entropy governed to directed by filament bending and then, to eventually dominated by filament stretching as deformation progresses [11].

Given that a wide variety of crosslinking proteins, with distinct physical properties, are involved in constructing the cytoskeleton of cells [13], the model developed in [11], has also been extended recently to examine how the deformability of cross-linkers regulates the bulk mechanical response and failure of biopolymer networks [14]. In that study, as shown in Figure 2(b), the crosslinking molecule was modeled as a combination of linear and angular springs that resist both the separation and rotation of two filaments.

In addition, the cross-linker was assumed to break once the strain energy stored inside is over a critical level. Interestingly, it was observed that the stress-strain curve of biofilament networks often shows transitions from linear increasing, to strain hardening, to stress serration and eventually to total fracture because of the interplay between the bending and stretching of individual filaments as well as the deformation and breakage of cross-linkers. Furthermore, the network fracture energy was found to reach its minimum at intermediate rotational compliance of crosslinking molecules, reflecting the fact that the imposed deformation tends to be evenly distributed among soft crosslinkers (with high rotational compliance) while most strain energy will be stored in the distorted filaments with rigid crosslinking proteins [14].

Conclusion

In this minireview we discussed some of the main continuumlevel simulation approaches that have been developed to study the response of semiflexible biopolymer networks in the last few decades. It must be pointed out that, besides these methods, constitutive modeling [8,15,16], and Brownian dynamics-based simulations [17-19], have also been widely used in this area, refer to [20,21], for a more comprehensive discussion. With help from the experimental side, it is conceivable that more biological features can be incorporated into different continuumlevel computational platforms in the future, allowing us to systematically examine important issues like the motility [22,23], volume regulation [24,25], and shape transformation [26,27], of cells where cytoskeleton dynamics is known to play a key role. In addition, these simulation tools can also provide insights for the development of active biomimetic materials [28,29] in the future.

CTBEB.MS.ID.556005

Our Media Partner

CTBEB Menu

Useful Links

Downloads