Stochastic Mechanism of Formation of Mutational Protein Nanoparticles and Mesoobjects
Emil Edypovich Lin*
Russian Federal Nuclear Center – All-Russia Research Institute of Experimental Physics, Institute of Physics of Explosion, Russia
Submission: February 06, 2019; Published: Febrauary 19, 2019
*Corresponding author: Emil Edypovich Lin, Research Associate, Russian Federal Nuclear Center – All-Russia Research Institute of Experimental Physics, Sarov, Russia
How to cite this article: Emil E L. Stochastic Mechanism of Formation of Mutational Protein Nanoparticles and Mesoobjects. Curr Trends Biomedical Eng & Biosci. 2019; 18(3): 555986. DOI: 10.19080/CTBEB.2019.18.555986
Abstract
We consider briefly a possible stochastic mechanism of formation of mutational protein nanoparticles and mesoobjects (cells and organelles). Results based on the uncertainty relation “coordinate – momentum” in the space of object (molecular cluster) sizes are indicative of the fact that in the system of amino acid molecules accidental formation of quasi-crystalline nanoparticles and mesoobjects corresponding in their sizes to essential proteins and cells is possible without of the preliminary formation of polypeptide nanochains. The developed kinetic approach and calculated results can be useful for laboratory investigation of a behavior of biological systems at different environments.
Keywords: Protein nanoparticles; Cells; Organelles; Mutations; Stochastic mechanism; Kinetic approach
Introduction
One of topical trends of nanoscience and nanotechnology consists in the creation and the study of biological materials, in particular, the study of physical mechanisms of protein biosynthesis [1,2]. In accordance with the results of the investigations the commonly accepted scheme of proteins construction is presented in such a manner that a volumetric-packed nanoparticle that represents an aperiodic crystal, is formed from nanochains with the C-N peptide bonds (primary structures) as a result of the twisting and the mutual arrangement of various polypeptides in the presence of nucleic acid molecules. At the same time, in works [3,4], there is another scheme of arrangement of biological nanoparticles, in which as a result of rotational-vibrational interaction of amino acid molecules, their direct volumetric polycondensation can occur. The seeding centers of polycondensation can be the molecules of nucleic acids, around which amino acid molecules are grouped. They are grouped in a certain order given by preferable formation of C-N bonds as the most short and strong bonds as compared to C-C and C-O bonds. In the proposed way of considering the corresponding mechanism of protein nanoparticle synthesis, the principle of uncertainty assumes the possibility of mutation of biological objects at a molecular level. In this work we specify and extend model ideas about stochastic kinetics cluster mechanism of formation of mutational protein nanoparticles as well as mesoobjects - cells and organelles.
Methodology
We will describe the process of the irreversible aggregation of objects using the concept of distribution density wave φ(a,t) in the space of cluster sizes a. The wave propagates with the time t toward an increase in the cluster size. Such one-dimensional approach allows one not to take into account deviation of a geometric shape of the object from the ideal one. On the assumption of the above the universal relation Δa⋅Δk≥1/4π [5] (kis wave number) for a wave packet half-width and a spectral line half-width for coherent processes one can write down the following uncertainty relation for a coordinate and a momentum in the space of cluster sizes:
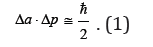
Here, Δp∼p=mΔa/Δt is momentum uncertainty, m=αρa3≅m0 (a/a0)is cluster mass, α is geometric factor, ρ is the density of cluster matter, m0a0 are the mass and size of germ, is reduced Planck constant. Momentum uncertainty is equal to the momentum itself in the order of magnitude, i.e., interaction of objects either occurs or does not occur. Physical meaning of relation (1) is in the fact that during the time interval tΔ of elementary (single) act of interaction between objects the exact cluster size cannot be determined until this interaction is finished either through capture of one object by another or their partial or complete disruption, or elastic scattering. It is connected with the fact that unless the elementary act is finished, it is impossible to determine to which object each of the interacting surface elements is assigned. In ours case such elements are amino acid molecules - the germs of biological objects. This means that uncertainty principle admits mutations of biological objects at a molecular level.
An evolution of distribution density function φ(a,t) during a stochastic process of aggregation can be described in diffusion approximation using FokkerPlanck equation written for the space of cluster sizes:

Here ν = da dt, η = (da)2 dt = 2m are the average rate of kinematic transport of φ and diffusion coefficient in the space a , respectively. A linearization of equation (2) allows us to establish basic characteristics of distribution density and to deduce the expressions for asymptotic growth laws of large clusters mean sizes ( 0 a >> a ) with the time. The obtained in [4] solution of linearized Eq. (2) with the help of Ventzel-Kramers-Brillouin method gives the following formula for relative distribution density of objects in sizes:

Here 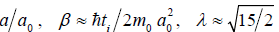 (this value was obtained
by sewing together solution for small clusters with the size
of germ), i t is characteristic time scale of elementary act of objects
interaction. Space factor of the function φ was normalized on the
“amplitude” (β 2)1 4 (1 λ )1 2 for germ. Formula (3) indicates on the
existence of discrete set of most probable cluster sizes:
(this value was obtained
by sewing together solution for small clusters with the size
of germ), i t is characteristic time scale of elementary act of objects
interaction. Space factor of the function φ was normalized on the
“amplitude” (β 2)1 4 (1 λ )1 2 for germ. Formula (3) indicates on the
existence of discrete set of most probable cluster sizes:
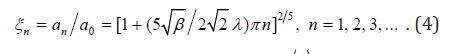
General growth law of mean size (a) has the following form:
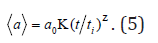
Here, Κ, Ζ are constants determined by the mode of cluster aggregation. At the first step we consider two limiting growth modes:
1) small flux of germs, when each germ has time to occupy its energy advantageous place on cluster surface before interaction with the following seed begins;
2) large flux of germs, when they affect the cluster almost simultaneously which is equivalent to cluster collision. In the first case ti parameter does not depend on a cluster size and the growth law can be written as
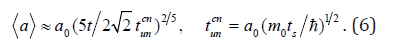
Here, cn un t is the time unit in the mode of small flux of germs, s t is the time of germ capture by surface of cluster. In case of germ large flux we accept the i t parameter equal to the perturbation back-and-forth travel time in a cluster:Δt ≡ ti =2(a)/c0, where 0 c is velocity of perturbation spread in cluster substance (sonic velocity). Then the law of growth can be written as
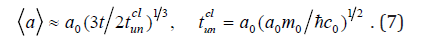
Here cl tun is the time unit in the germs large flux mode (cluster collision).
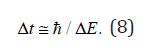
In number of problems connected with investigations of high-intensive processes with high energy (for example, at high temperatures T of crystal objects) it is reasonable to determine the value of Δt time interval of elementary interaction act based on the “energy-time” uncertainty relation (Heisenberg rule): Δt ≅ / ΔE. (8) Here ΔE is energy level width of an isolated excited state of a quantum mechanical system. Substituting expression (8) in relation (1) rewritten for the mean size, and taking into account that the mean size is changed with the time by uninterrupted manner, one can write the following differential relation:
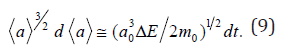
Here value is determined by nature of objects and a process mode and can be depends from the mean size a of the excited field. Having solved differential relation (9) in quadratures one can find approximate laws of mean size a growth with time in high-intensive processes of object aggregation. On the basis of the relation (1) and the condition of mass conservation ρ3a3+pa0 = ρ( a + Δa)3 during single act of interaction between cluster and germ one can deduce the following expression for maximal object size:
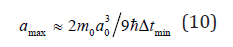
Here min i Δt ≡ t is minimal time interval of an elementary act of object interaction determined by physical nature of the process.
In the case of long and thin nanostructures (nanofibers) one
can deduct from the relation (1) and the condition of mass conservation
during single act of germ connection to vacant nanofiber
end 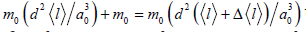 the following expressions
for determining characteristic values of thickness d and
length l of continuous nanofiber:
the following expressions
for determining characteristic values of thickness d and
length l of continuous nanofiber:
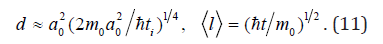
In the case of hollow nanofiber (nanotube) the diameter is determined by analogy with single-wall carbon nanotube [6] with the help of following formula:
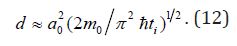
Calculated Results and Discussion
We consider the molecules of glycine (m0 = 1.25·10–25kg, a0 = 0.42nm), alanine (m0 = 1.49·10–25kg, a0 = 0.47nm), valine (m0 = 1.95·10–25 kg, a0 = 0.54 nm) and tryptophan (m0 = 3.7·10–25kg, a0 = 0.67nm) [1] as the germs. For the basic level ( j 1) r E = of the rotary binding energies C–C, C–O, and C–N, we have:
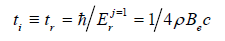
Here e B is a rotary constant [7]. For the given bonds the values of the rotary constant are within the small range (1.817–1.93)∙102 m–1, therefore, to determine the time unit, the average value e B = 1.88∙102 m–1 was taken, hence, r i t≡ t ≈ 1.4∙10–12 s. . For the ground level of the oscillating binding energies C–C, C–O and C–N we have:
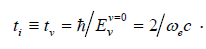
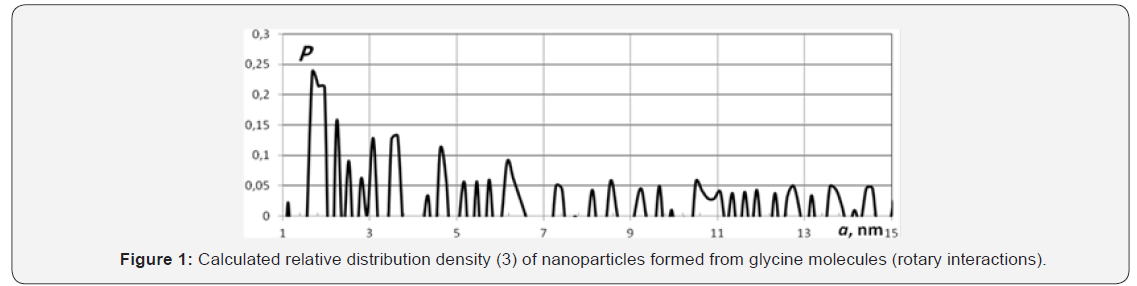
Here e ω is a wave number of characteristic oscillations which for the given bonds is equal approximately to 2·105 m–1 [7]. From here we have i v t ≡ t ≈ 3.3·10–14 s. Figure 1 presents the example of relative distribution density (3) and demonstrates the existence of discrete set of sizes of nanoparticles formed from germs. Set of calculations performed with the help of formulae (3), (4) for all mentioned germs at above time i r t ≡ t , corresponding to basic rotational level, allows one to single out the following typical neighborhood and “magic” sizes: r mag a = (1.4–1.7), (2.2–2.5), (2.7–2.9– 3.3), (4–4.6–4.7), (5–5.5–5.6), (6–6.7–7), (8–8.5), 9, 10, 11, 12, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23nm. These sizes correspond to proteins [1,2,8].
Let us consider the expressions for mean sizes of protein nanoparticles and mesoobjects. At Debye approximation one can rewrite the formulae (6), (7) by following manner:
i. for small flux of germs
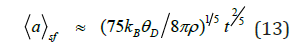
ii. for large flux of germs
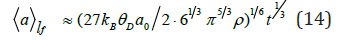
It has been supposed that Debye parameter D θ corresponds approximately to average characteristic temperature v θ ≈ 1500 K [9] of extension vibration of bonds C–C, C–O, C–N. Using expression (9) for high intensive processes one can write the growth laws by following manner:
iii. for small flux of germs

iv. for tangent interaction (shear mechanism)
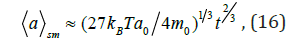
v. for simultaneous excitation of the system)

Dependences (13), (14) as well as dependence (15) at T = 310 K in time range t≈10 10 10 7 − − ≈ of conformational motion [2] envelop characteristic sizes [1,2] of protein nanoparticles from ≈2nm to ≈60nm. Tangent interaction between amino acid molecules at shear processes resulting from mechanical action to system leads to significant magnification of sizes of biological objects under consideration to 800nm at t ≈10-7 s); and simultaneous excitation of the system at absorption of energy of emanation having different nature leads to formation of low density lipoproteins (≈20nm at s) and leucocytes (≈20μm at t ≈10-7 s).
With the typical parameter [9] 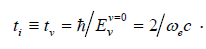 corresponding
to rotational molecule isomerism (b is a number of crystal-
forming bonds, R θ is the typical rotational bond temperature
(≈2.6 K), T is ambient temperature), we derive from the formula
(11) that for the germs like glycine and tryptophan at T ≅ 310 K,
the diameters d of nanofibres are equal to 1.27nm and 2.35nm.
These values approximately correspond to the thicknesses of collagen
protein (~1 nm [1]) and myosin protein (2.5nm [2]). If we
assume that to form the nanofibre thickness, it is sufficient to have
a single oscillation of a “last bond” of the longest molecule of tryptophan
and i t ≈ 3·10–14 s , then from the formula (11) we get d ≅ 12
m . This approximately corresponds to the thickness of a continuous
neurofibril of a human, neurofilament, approximately equal
to 10nm [10]. If we consider alanine molecule as the germ, then
in case of vibrational interaction we get from the formula (12) d
≈ 20 nm. This approximately corresponds to the diameter of human
hollow neurofibril, approximately equal to 20-25 nm [10].
Calculation shows that to form a neurofilament 300nm long, one
requires approximately 100 μs.
corresponding
to rotational molecule isomerism (b is a number of crystal-
forming bonds, R θ is the typical rotational bond temperature
(≈2.6 K), T is ambient temperature), we derive from the formula
(11) that for the germs like glycine and tryptophan at T ≅ 310 K,
the diameters d of nanofibres are equal to 1.27nm and 2.35nm.
These values approximately correspond to the thicknesses of collagen
protein (~1 nm [1]) and myosin protein (2.5nm [2]). If we
assume that to form the nanofibre thickness, it is sufficient to have
a single oscillation of a “last bond” of the longest molecule of tryptophan
and i t ≈ 3·10–14 s , then from the formula (11) we get d ≅ 12
m . This approximately corresponds to the thickness of a continuous
neurofibril of a human, neurofilament, approximately equal
to 10nm [10]. If we consider alanine molecule as the germ, then
in case of vibrational interaction we get from the formula (12) d
≈ 20 nm. This approximately corresponds to the diameter of human
hollow neurofibril, approximately equal to 20-25 nm [10].
Calculation shows that to form a neurofilament 300nm long, one
requires approximately 100 μs.

The calculated dependences (10) of maximal sizes of biological nanoparticles and mesoobjects from germ sizes at basic state and at first excited of rotatory and oscillating levels are given in Figure 2. When molecules move from the first rotary level (j = 1) to the second level (j = 2) or from the “zero” oscillating level (v = 0) to the first level (v = 1), the maximum sizes will increase a factor of 3, since the energy of rotations is quantized ( 1) 2 , 1, 2, 3, ... R e E = j j + B π c j = as and the energy of oscillation is quantized approximately as v ( 12 ) e , 0,1, 2, 3, ... E = v + ω c v = (for the bonds under consideration inharmoniousness factors are small [7]). Formally this means that with rotary motions when germs are glycine molecules (a0 = 0.42nm) a size of about 40nm corresponding to a ribosome of eukaryotes is reached. If germs are tryptophane molecules (a0 = 0.67nm), a size of about 450 nm is reached which corresponds to nanoarcheot [11]. At oscillating motions in case of alanine as the germ (a0 = 0.47nm) a size of 3μm is reached which corresponds to a thrombocyte [1]; in case of tryptophan seed a size of 20μm is reached. The latter means that in the system there can be formed leucocytes whose sizes are within the range from 8 to 15μm [1]. At the second level of oscillations (v = 2) sizes of leucocytes can be reached if germs are valine molecules (a0 = 0.54nm). This fact does not contradict to the known medical facts of formation of mutations and tumors or development of atherosclerosis and leukemia under the effect of ray penetration into an organism.
Thereby, the results from the uncertainty relationship “coordinate- momentum” in the space of object sizes are indicative of the fact that in the system of amino acid molecules, accidental formation of quasi-crystalline nanoparticles and mesoobjects corresponding in their sizes to essential proteins and cells is possible. These “incorrect” (mutational) objects can grow on these or those crystallization centers without formation of polypeptide bonds, i.e., without formation of “correct” biological code. At the same time formation and growth of such nanoparticles and mesoobjects is possible on fragments of damaged proteins and cells as on the centers of crystallization. All this is in compliance with the generally known concepts concerning mutations of biological structures at a molecular level.
It is necessary to note that the above formulae deduced from the uncertainty relations in the space of object sizes correspond to condition of mass conservation during elementary act of interaction between a germ and an object. These formulae are not tied together with the condition of mass conservation in the whole system. A system can be unclosed in accordance with a general nature of biological processes [1,2,8]. Organic-silicon mesoobjects have been considered also in [12]. The basis of these meso objects is siloxane sceleton – the chain of alternate Si and O atoms. Elementary portion of such polymer chain consists of two adjacent atoms Si and attached atoms C, H, O. Replacement of some H atoms by N, P, S, and Fe atoms results in analogy with biological polypeptide nanochains [1, 2]. Such analogy expands a range of questions related to the study of life as a nanoscale phenomenon [8]. Based on the well-known data [7] on atomic radii and the lengths of interatomic bonds, the characteristic sizes of globular organic-silicon nanocrystals have been evaluated in [12]. The obtained sizes 60nm and 4μm correspond to the sizes of biological equivalents (ribosomes) and to biological mesoobjects [1]. The issue of existence of such hypothetical biological structures, containing silicon, remains open. It looks reasonable to search for the mentioned structures in places, where rubber-bearing plants grow. The developed kinetic approach and calculated results can be useful for laboratory investigation of a behavior of biological systems at different environments.
Abstract
Keywords:
Acknowledgement
The author is grateful to Dr. Evgeniya Petrovna Lobkaeva for the support of this work.
References
- Pool CP, Owens FJ (2003) Introduction to Nanotechnology. A John Wiley & Sons, Inc.: London, UK.
- Suzdalev IP (2006) Nanotechnology: Physics-Chemistry of Nanoparticles, Nanostructures and Nanomaterials. Synergetics: From the Past to Future, Komkniga, Moscow.
- Lin EE (2016) Cluster Mechanism of Formation of Biological Nanoobjects and Mesoobjects. Physical Science International Journal 11(2): 1-5.
- Lin EE (2017) Kinetics for Formation of Objects Based on Carbon Nanostructures. Lambert Academic Publishing, Germany.
- Persico E (1963) Fundamentals of Quantum Mechanics. Prentice-Hall.
- Lin EE (2003) On the Growth Kinetics of a Single-Wall Carbon Nanotube. Doklady Physics 48(4): 180-181.
- Ravdel AA, Ponomareva AM (1983) Handbook of Physical-Chemical Values. Leningrad: Khimia.
- Mann S (2008) Life as a Nanoscale Phenomenon. Angewadte Chemie International Edition 47: 5306-5320.
- Syue-sen T (1965) Physical Mechanics. Mir, Moscow.
- Neurofibriles (1974) Big Soviet Encyclopaedia, Soviet Encyclopaedia. Moscow, Russian 17: 1244.
- Huber H, Hohn MJ, Rachel R, Fuchs T, Wimmer VC, et al. (2002) A new Phylum of Archaea represented by a nanosized symbiont. Nature 417(6884): 63-67.
- Lin EE (2018) Revealing the Uncertainty and Absolute Certainty Principles in the Kinetics of Objects Formation. World Journal of Mechanics 8(4): 82-93.






























