Research Article

Computational Tool for Calculation of Tissue Air Ratio and Tissue Maximum Ratio in Radiation Dosimetry

Atia Atiq*, Maria Atiq and Saeed Ahmad Buzdar

Department of Physics, The Islamia University of Bahawalpur, Pakistan

Submission: November 27, 2018;Published: January 03, 2019

*Corresponding author: Atia Atiq, Department of Physics, The Islamia University of Bahawalpur, Pakistan

How to cite this article: Added Atia A, Maria A, Saeed A B. Computational Tool for Calculation of Tissue Air Ratio and Tissue Maximum Ratio in Radiation Dosimetry. Curr Trends Biomedical Eng & Biosci. 2019; 17(4): 555966. DOI:10.19080/CTBEB.2019.17.555966.

Abstract

The radiation therapy field is advancing continuously to achieve higher degrees of accuracy and efficiency. The purpose of this work is to enhance the efficiency of radiotherapy machine commissioning by applying computational tools to interpolate dosimetric quantities Tissue Air Ratio (TAR) and Tissue Maximum Ratio (TMR). Newton Divided Difference interpolation method was used to interpolate data between tabulated values. In order to shorten the commissioning time, technique of interpolation was used; in which calculation of dosimetric quantities were made for certain depths and field sizes with reasonable step size and remaining values at different depths and field sizes were obtained by interpolation. It was found that interpolated results considerably agree with the measured data and so this method could be used efficiently for interpolation of above mentioned dosimetric quantities. The data obtained by this technique is highly reliable and can fill the discrete set of tabulated data to make it continuous. The results obtained in this technique were in agreement with measured data and hence could be used as input data in radiotherapy treatment planning process. The interpolated results were well within accuracy limits and this method can significantly improve the efficiency of machine commissioning and resultantly improve treatment planning process.

Keywords: Radiotherapy; Interpolation; Tissue maximum ratio; Tissue air ratio; Commissioning

Abbrevations: PDD: Percentage Depth Dose; TMR: Tissue Maximum Ratio; TAR: Tissue Air Ratio; SSD: Source to Surface Distance; BJR: British Journal of Radiology

Introduction

In radiation therapy, it is essential to calculate the dosimetric quantities such as Percentage Depth Dose (PDD), Tissue Air Ratio (TAR), and Tissue Maximum Ratio (TMR). The basic depth dose data was determined by dosimetric measurements taken in dummy patients (phantoms), which have density nearly equal to human body tissues, with ionization chamber placed in them [1]. A system for absorbed dose calculations has been developed to foresee the depth dose distribution in patients going to be treated. The radiation dose deposited by ionizing radiations within the patient or medium varies with the varying depth. This variation is due to different parameters like depth, beam energy, field size, Source to Surface Distance (SSD). While calculating absorbed doses, greater considerations must be given to these parameters as they cause changes to depth dose distributions [2]. Plenty of radiotherapy units, such as linac and cobalt-60 units, accomplish the treatment of cancerous parts. To treat cancerous tissues, cobalt 60 gamma ray beam is used for more than fifty years in radiotherapy [3].

Nowadays these units are used in conjunction with computer-controlled devices [4]. Determination of dosimetric characteristics of all radiation beams is important so that most appropriate set of treatment planning parameters is chosen. Dosimetry is vital element of treatment using radiation as all the treatment planning is based on data obtained during dosimetry [5]. To ensure that malignant part get the prescribed dose, it is essential to perform dose calculation by managing radiation beams which are characterized by various parameters in the treatment machine. This process of delivering radiations is called treatment planning. In advanced radiation techniques, treatment planning is generally performed with computing software’s. These software’s are used for identifying and locating anatomy of patients and the machine parameters to simulate the actual treatment [6]. We intended to increase the efficiency of the radiation therapy by applying mathematical and computational tools not only to verify the measured dosimetric data but also to aid in rapid machine commissioning.

Material and Method

In the process of treatment planning many methods have been adopted to calculate variation of dose in the patients. Percentage Depth Dose (PDD) and Tissue Phantom Ratio (TPR) are among the two methods used for photon beams. First method devised for the calculation of dose was PDD but it has restriction that it depends on Source to Surface Distance (SSD) and this limitation was overcome by introducing a simpler quantity TPR [7]. Although dependence of PDD on Source to Surface Distance can be overcome by the use of quantity Tissue Air Ratio (TAR) but its usefulness is only for beams having low X-ray energies i.e. in gamma beam radiotherapy, so this quantity was in use when high-energy beams were not common.

The quantity TAR can be defined as the quotient of absorbed dose with a certain depth in phantom to the absorbed dose at the same depth in free space [8].

Where D_b is the absorbed dose at certain point d in phantom and D_fs is the absorbed dose in free space at the same point. The limitation of TAR for megavoltage units is because of the fact that at high beam energies it becomes cumbersome to make measurements in air [9]. With high energy beams it become difficult to make measurements in air so we can say that Tissue Phantom Ratio TPR and Tissue Maximum Ratio TMR are the alteration of Tissue Air Ratio, which makes them acceptable to be used for high energies. Tissue Phantom Ratio is defined as the quotient of absorbed dose at a given depth d to the absorbed dose at fixed reference depth in water phantoms [10,11].

Where t0 is taken to be the reference depth. Although TPR can be normalized to any reference depth but for most clinical purposes, 5cm is taken to be the reference depth. TMR is the special case of TPR in which reference depth is taken to be the depth of maximum dose D_{d max} [12].

Because of insensitivity of TMR on SSD, it has been found useful for isocentric treatments whereas for any variation in SSD inverse square correction must be applied for dose calculation by PDD [13]. TAR and TMR should be measured with great care as they vary with varying field sizes and increasing depths. This entire commissioning process must be performed methodically and steadily which may require several months. Dosimetric data is obtained for certain depths and field sizes in phantom. However, it is time consuming to generate dosimetric values for all depths and field sizes. As it is desirable to save time and improve the efficiency of radiotherapy process, so values of TAR and TMR are calculated for some field sizes and depths with discrete step size and the rest of data is obtained by interpolation. This work aimed at enhancing the efficiency of treatment plan and for this purpose Newton Divided Difference Interpolation method had been used to calculate absorbed doses at various depths first by keeping field size constant and then at various field sizes by keeping depth constant. Newton divided difference method is the polynomial interpolation technique used for obtaining intermediate values and is based on difference tables [14,15]. This method was preferable because it finds no difficulty in calculating interpolated values for those data points that neither are in definite sequence nor are equally spaced. Important characteristics of this method are as follows.

i. In interpolation, the values of x may or may not be equally spaced.

ii. The x values used in interpolation can be randomly selected i.e. increasing suffix of x does not mean that values of x are also increasing.

For pictorial understanding of this method, table for five data points is shown in Table 1. This work aimed at calculating, interpolating, and analyzing Tissue Air Ratio for Cobalt-60 Gamma ray beams and Tissue Maximum Ratio for 4 MV and 6 MV photon beams at different depths and field sizes.

Results and Discussion

One of the most important factors in the process of treatment using radiation beams was to determine dose characteristics such as TAR and TMR. Interest was to determine these characteristics mainly because aim of this work was to use this data in treatment planning process and also to study physics behind radiation beams. The main objective of this work was to evaluate, measure and calculate dosimetric characteristics using Newton Divided Difference interpolation technique.

Calculation of TAR and TMR at Constant Field Size and Varying Depths

The data presented in this work was of Tissue Air Ratio for Cobalt-60 Gamma ray beams. Tables 2 & 3 represented values of TAR and TMR at constant field size and varying depth respectively. Tables were drawn with depths varying from 1 cm to 26 cm. Step size was taken from 1 cm to 20 cm depths and after that only even numbered depths are taken i.e. 22 cm, 24 cm and 26 cm. The depth of 1 cm had been assigned depth of maximum dose i.e. dm [16]. With increasing depth, values of TAR decreased as was clearly depicted in Table 2. For the purpose of interpolation, separation was chosen to be 5 cm. In Table 2, depths were varied keeping field sizes constant. Field sizes were selected from 4 x 4-cm² to 75 x 75-cm2, and field size represented in Table 2 was 7 x 7-cm².

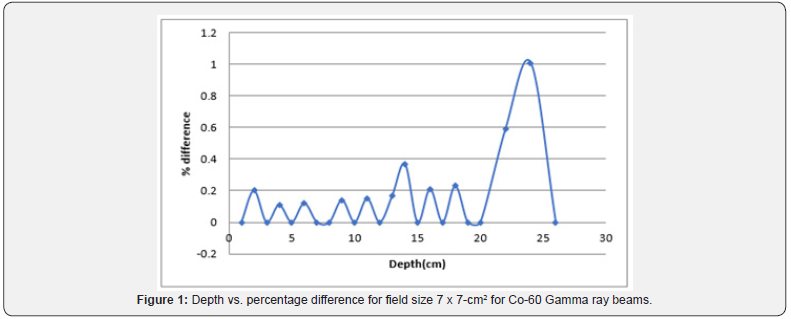
In Table 2, Tissue Air Ratio was interpolated at certain depth. The calculated TAR data showed the same trend as the measured data. Similar results were observed for TMR, as represented in Tables 3 & 4, proving that it is possible to interpolate any value between given measured values. Minor variation was observed in measured and interpolated values of TAR and TMR. Percentage difference between interpolated and measured values of two basic dosimetric quantities were calculated. Interpolation was done using Newton Divided Difference Method and measured values were taken from British Journal of Radiology (BJR) supplement 25, and calculated results was found to be within limits of accuracy i.e. percentage difference was less than 2%. So interpolated TAR values were consistent when compared with standard data. It was to be noted that there was no general rule in the variation of percentage difference of calculated Tissue Air Ratio. They varied randomly at different depths but remain within the boundaries of accuracy. The results between percentage difference and depth for TAR values were also presented graphically in Figure 1. The figure was plotted between depth on x-axis and percentage difference on y-axis.

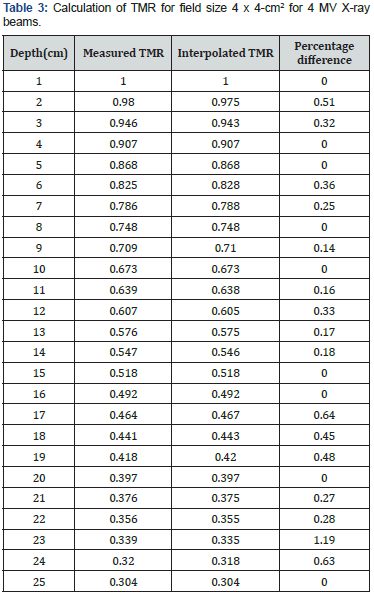
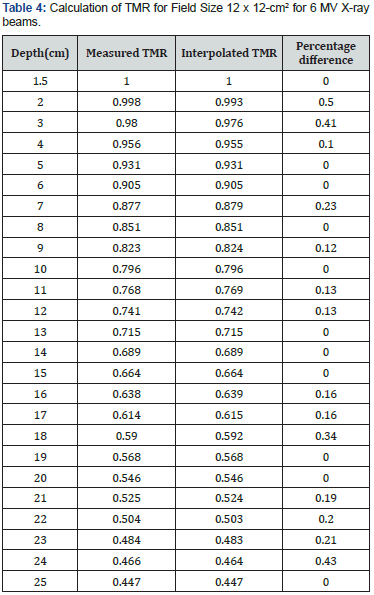
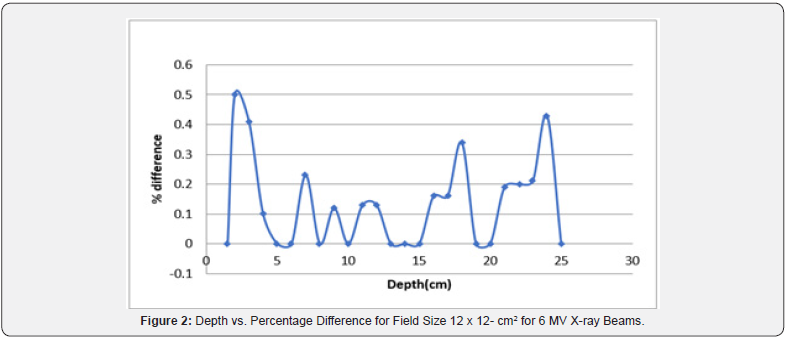
For carrying out interpolation of TMR values, 4 MV & 6 MV photon beams were used. In Table 4, TMR values were calculated for field size of 12 x 12-cm2 while varying the depth from 1 cm to 25 cm. Calculations were carried out at depths with 5 cm separation and divided difference method was used to calculate TMR in between these depths. The field sizes were set from 4 x 4-cm² to 40 x 40-cm². It was further observed that for 4 MV X-ray beams, the calculated results were in close agreement with the measured data. Considering Table 3, by keeping the separation to be 5 cm, the interpolation of TMR data was performed for 6 MV X-ray beams. The calculated data was then compared with measured data and percentage difference between interpolated and measured data was found. Percentage differences of interpolated TMR from measured TMR were almost 2% or even less, which is the limit of accuracy requirement. The results between percentage difference and depth for TMR values were also presented graphically in Figure 2. These results can further be extended by applying interpolation method for varying field sizes and constant depths to prove the robustness of this technique.

Calculation of TAR and TMR at Constant Depth and Varying Field Size

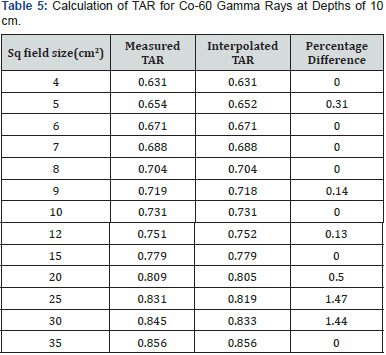
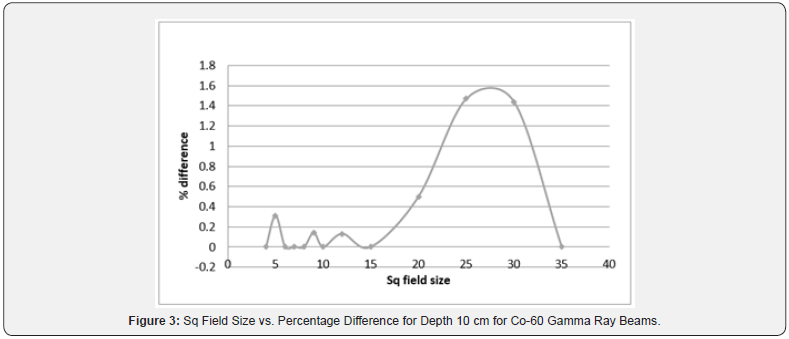
For TAR, depths were kept constant at 5 cm and 10 cm while field sizes varied from 4 x 4-cm2 to 35 x 35-cm2. Interpolation points were kept at field sizes 4 x 4-cm2, 8 x 8-cm2, 15 x 15-cm2 and 35 x 35-cm2. The maximum percentage difference in Table 5 was 1.47% at the field size of 25 x 25-cm2. There was no percentage difference at the field sizes 6 x 6-cm2, 7 x 7-cm2 and 10 x 10- cm2. Results were also graphically plotted in Figure 3 taking field size at x-axis and percentage difference at y-axis.

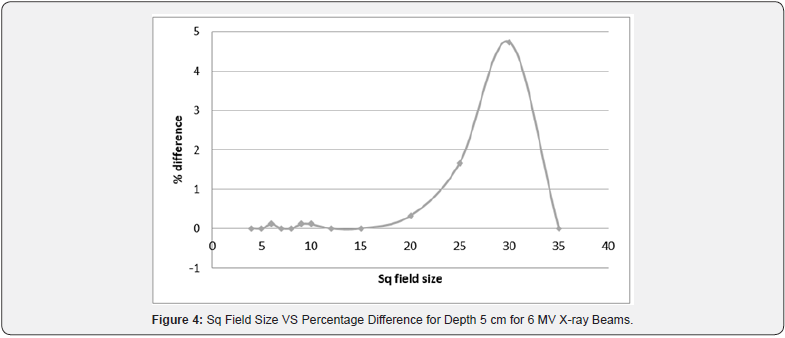
For TMR, the variation for field sizes from 4 x 4-cm2 to 35 x 35- cm2. The points of interpolation were set at field sizes 4 x 4-cm2, 8 x 8-cm2, 15 x 15-cm2, and 35 x 35-cm2. Table 6 represented TMR values for 6 MV X-ray beams at constant depth of 5cm and the interpolated results were observed to be quite satisfactory. Percentage difference was zero for field sizes 5 x 5-cm2, 7 x 7-cm2 and 12 x 12-cm2. The differences were close to zero for field sizes 6 x 6-cm2, 9 x 9-cm2 and 12 x 12-cm2. The maximum percentage difference was noted at the field sizes of 30 x 30-cm2 and it was found to be 4.74%. Results were also graphically plotted in Figure 4 taking field size at x-axis and percentage difference at y-axis.

By analyzing the results thoroughly it was established that Newton Divided Difference method could be used as an efficient method for interpolating accurate values both for varying depths and varying field sizes and also data calculated using this method was accurate enough to be used as an input data in the process of radiotherapy, thus increasing the effectiveness of radiotherapy process while reducing time period.

Conclusion

This work mainly focused on finding the ways to improve the treatment planning process. This work suggested an efficient numerical method to calculate dosimetric parameters Tissue Air Ratio TAR and Tissue Maximum Ratio TMR that could be useful for medical physicists in increasing the accuracy of radiotherapy treatment practice. The Divided Difference method was applied in this work to calculate TAR and TMR at different depths and field sizes with the reasonable step size and remaining values were interpolated to obtain continuous data set. The results obtained in this technique were in agreement with measured data and hence could be used as input data in radiotherapy treatment planning process. To facilitate the radiotherapy treatment planning process, further it was recommended to interpolate different dosimetric quantities by using different methods of numerical analysis and to compare those results. Additionally, different interpolation techniques could be explored to find the best one, which will be helpful in reducing the error.

Conflict of Interest

Authors declared that there is no conflict of interest.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional research committee Shaukat Khanum Memorial Cancer Hospital and Research Centre.

Informed Consent

For this type of study, formal consent is not required.

References

1. Abdul Haneefa K, Cyriac TS, Musthafa MM, Ganapathi Raman R, Hridya VT, et al. (2014) FLUKA Monte Carlo for Basic Dosimetric Studies of Dual Energy Medical Linear Accelerator. Journal of Radiotherapy. p. 7.
2. Podgorsak EB (2005) Radiation oncology physics. A handbook for teachers and students. Br J Cancer 98(5): 1020.
3. Khan FM (2003) Physics of Radiation Therapy. Lippincott, Williams & Wilkins, USA, 2003.
4. Van Dyk J, Battista JJ (1996) Cobalt-60: An old modality, a renewed challenge. Curr Oncol 3: 8-17.
5. Xhafa B, Mulaj T, Hodolli G (2014) Dose Distribution of Photon Beam by Siemens Linear Accelerator. International Journal of Medical Physics Clinical Engineering and Radiation Oncology 3: 67-70.
6. Lanchun L (2013) Dose Calculation Algorithms in External Beam Photon Therapy. International Journal of Cancer Therapy and Oncology 1(2): 01025.
7. Dyke L (1997) Development of a Clinical MRI Dosimeter (Master of Science thesis). Edmonton, Alberta: University of Alberta 1997.
8. Suresh K Agarwal, Ronald V, Scheele, Wakley J (1971) Tissue Maximum- Dose Ratio for 8 MV X-rays. Charlottesville, Virgina 112(4): 797-802.
9. Bruce G, Haffty, Lynn D Wilson (2008) Handbook of Radiation Oncology: Basic Principles and Clinical Protocols. Ontario, Jones and Bartlett Publishers.
10. Jayaraman SH, Lanzl L (2004) Clinical Radiotherapy Physics, Berlin, Springer-Verlag.
11. Ding G, Krauss R (2013) An Empirical Formula to Obtain Tissue Phantom Ratios from Percentage Depth Dose Curves for Small Fields. Phys Med Biol 58(14): 4781-4789.
12. Sen A, West MK (2009) Commissioning Experience and Quality Assurance of Helical Tomotherapy Machine. J Med 34(4): 194-199.
13. Buzdar S, Shamsi Q, Afzal M (2013) Verification of Absorbed Radiation Dose for X-rays through Langrange’s Interpolation Method. Pakistan Academy of Sciences 50(4): 309-314.
14. Melvin J, Maron (1982) Numerical Analysis: A Practical Approach, New York, Macmillan Publishing Co. Inc.
15. Buzdar S (2008) Optimization of Accuracy Concepts in Treatment Planning for Conformal Radiotherapy (Ph.D thesis), The Islamia University of Bahawalpur, Department of Physics.
16. Burns J (1996) Megavoltage X-RAY beams: 2-50 MV. BJR Suppl 25: 62- 109.