The Associated Factors of Direct Bilirubin for Liver Patients
Rabindra Nath Das*
Department of Statistics, The University of Burdwan, Burdwan, India
Submission: April 20, 2018; Published: June 11, 2018
*Corresponding author: Rabindra Nath Das, Department of Statistics, The University of Burdwan, Burdwan, West Bengal, India, Email: rabin.bwn@gmail.com
How to cite this article: Rabindra N D. The Associated Factors of Direct Bilirubin for Liver Patients. Curr Trends Biomedical Eng & Biosci. 2018; 15(3): 555913. DOI:10.19080/CTBEB.2018.15.555913.
Abstract
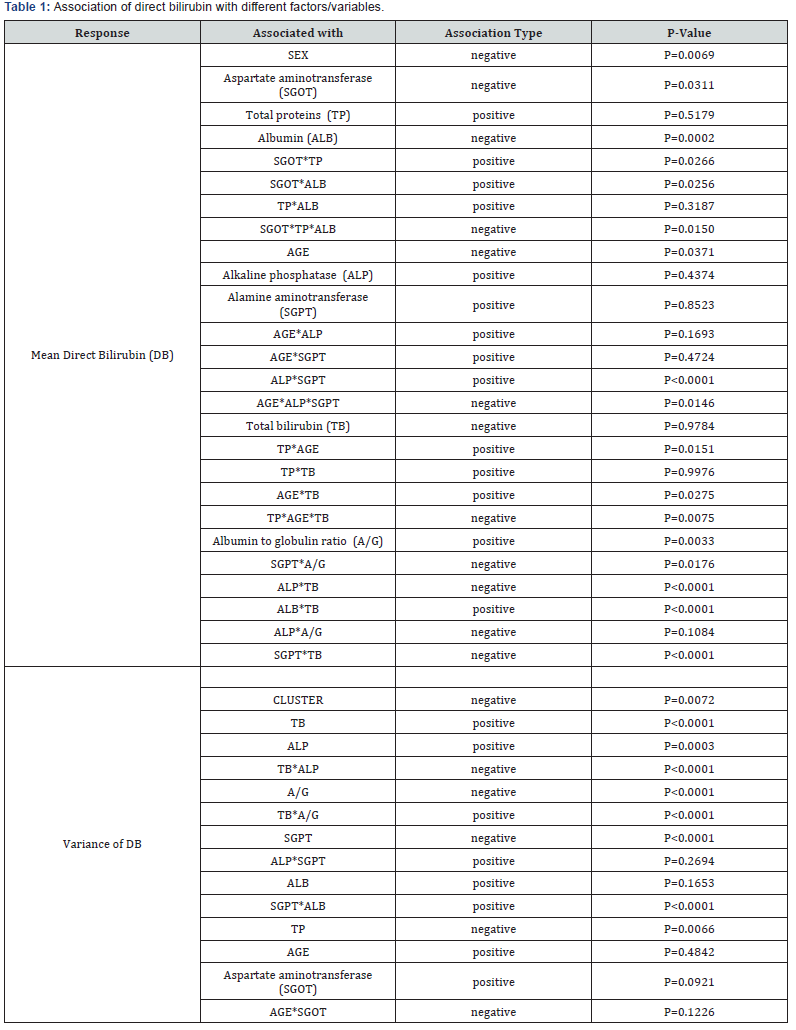
Direct bilirubin (DB) is a liver disease marker which is highly correlated with total bilirubin (TB), aspartate aminotransferase (SGOT), albumin (ALB), and many second and third-order interaction effects. It has a very complicated functional relationship with the other liver disease markers, total protein (TP), albumin (ALB), albumin & globulin ratio (A/G), age and sex. Three factor interaction effects such as SGOT*TP*ALB (P=0.0150), AGE*alkaline phosphatase (ALP)* alamine aminotransferase (SGPT) (P=0.0146) and AGE*TB*TP (P=0.0075) are significantly associated with the direct bilirubin. Consequently, their many second-order and marginal effects are significantly associated with the direct bilirubin.
Direct Bilirubin’s Explanatory Factors for Liver Patients
Bilirubin is a product of heme catabolism that may have potent cytoprotective and antioxidant properties [1,2]. Our body generally breaks down old red blood cells, consequently a substance is produced, which is known as bilirubin. It is also a part of bile, that is used by our liver to digest our eaten food. A small quantity of bilirubin in our blood is normal (0.22-1mg/dl), but a large amount may be an indication of liver disease. So, it is considered as a liver disease marker. The bilirubin which is bound to a certain albumin (protein) in the blood is called indirect or unconjugated bilirubin. Direct or conjugated bilirubin travels from the liver into the small intestine. A little quantity of bilirubin passes into our kidneys and is excreted in our urine. Due to this bilirubin, the urine gets its distinctive yellow color. Earlier research articles have shown that the liver patients with higher bilirubin levels are inversely associated with the insulin levels, the prevalence of coronary heart disease and diabetes mellitus [3-5]. The report aims to identify the associated factors of direct bilirubin for some liver and non-liver patients. The considered hypotheses are: What are the associated factors of direct bilirubin? How are the factors associated with the direct bilirubin? These hypotheses are evaluated with the help of a real data set given in [6,7].
The data set can be found in http://archive.ics.uci.edu/ml/machine-learning-databases/00225/”. It was collected from the North-East of Andhra Pradesh, India. The considered data set contains 579 subjects with 9 continuous variables such as age, direct bilirubin (DB), total bilirubin (TB), alamine aminotransferase (SGPT), alkaline phosphatase (ALP), aspartate aminotransferase (SGOT), albumin (ALB), total proteins (TP), and albumin to globulin ratio (A/G), and two attribute characters such as sex (male=0, female=1), types of patients (liver patient=1, non-liver patient=2) (CLUSTER). In the study, there are 28.5% non-liver, and 71.5% liver patients. Note that male subjects are 75.82%, while females are 24.18%. The mean, standard deviations, and the normal ranges of the above 9 continuous variables are displayed in [8], (Table 1). For the same data set, the determinants of alkaline phosphatase are derived in [8], using both the joint generalized linear Log-normal and Gamma models [9-12]. The response direct bilirubin is continuous, positive and heteroscedastic, so it has been analyzed both by the joint Log-normal and Gamma models, and it is found that joint Log-normal models fit gives better results than joint Gamma models fit. The current reported results in the article have been derived from the joint Log-normal models fit.
The study contains 11 explanatory factors/variables on 579 subjects of non-liver & liver patients. It is aimed in the report to examine the associated factors/variables of direct bilirubin. Therefore, the direct bilirubin (DB) is considered as the response variable, and the remaining other factors/ variables are considered as the explanatory variables. From the fitted joint generalized linear Log-normal models of the direct bilirubin, the following results are reported.
The fitted joint generalized linear Log-normal models of the direct bilirubin is very complicated, as it contains three 3-factor interaction effects such as SGOT*TP*ALB (P=0.0150), AGE* ALP*SGPT (P=0.0146) and AGE*TB*TP (P=0.0075) which are significantly associated with the direct bilirubin. Consequently, all their marginal and 2-factor interaction effects are included in the model due to the marginality rule given by Nelder [13]. Note that all the included effects in the joint Log-normal fitted models are not significant always [13,14].
In the joint Log-normal fitted mean model of direct bilirubin, the 3-factor interaction effect SGOT*TP*ALB (P=0.0150) is negatively associated with the DB. Its marginal effects SGOT (P=0.0311) and ALB (P=0.0002) are also negatively associated with the DB, while the marginal effect TP is insignificant (P=0.5179). Therefore, the marginal effects of SGOT, ALB, and the 3-factor interaction effect SGOT*TP*ALB have the same association with the DB, indicating that as their effects increase, direct bilirubin decreases. The three 2-factor join interaction effects of SGOT, TP and ALB are SGOT*TP (P=0.0266), SGOT*ALB (P=0.0256) and TP*ALB (P=0.3167) which are positively associated with the direct bilirubin. Note that first two 2-factor interaction effects are significantly associated with the DB, while the third one is partially associated. For these three 2-factors, if their effects increase, DB also increases. It is observed herein that that the marginal effects (of SGOT, TP and ALB), and the 3-factor interaction effects are negatively associated with the DB, while their three 2-factor interaction effects are positively associated with the DB.
In the fitted mean model of direct bilirubin, the 3-factor interaction effect AGE*ALP*SGPT (P=0.0146) is negatively associated with the DB. Only the marginal effect AGE (P=0.0371) is negatively associated with DB, while the marginal effects ALP (P=0.4374) and SGPT (P=0.8523) are insignificant. Therefore, as age or the 3-factor interaction effect increases, DB decreases. The three 2-factor join interaction effects of AGE, ALP and SGPT are AGE*ALP (P=0.1693), AGE*SGPT (P=0.4724) and ALP*SGPT (P<0.0001) which are positively associated with the direct bilirubin. Note that first 2-factor interaction effect is partially, the third one is significantly associated with the DB, while the second one is insignificant. It shows that if the 2-factor interaction effects increase, DB also increases. Here also, the marginal and the 3-factor interaction effects are negatively associated with the DB, but all the three 2-factors effects are positively associated with the DB.
In the fitted mean model of direct bilirubin, the 3-factor interaction effect AGE*TB*TP (P=0.0075) is negatively associated with the DB. Note that the marginal effect AGE (P=0.0371) is negatively associated with DB, while TB (P=0.9784) and TP (P=0.5179) are insignificant. Therefore, as age or the 3-factor interaction effect increases, DB decreases. The three 2-factor join interaction effects of AGE, TB and TP are AGE*TB (P=0.0275), AGE*TP (P=0.0151) and TB*TP (P=0.9476) which are positively associated with the direct bilirubin. Note that first two 2-factor interaction effects are significantly associated with the DB, while the third one is insignificant. It shows that if the 2-factor interaction effects increase, DB also increases. As in the above two cases, the same scenario is observed herein.
For the fitted mean model of direct bilirubin, the 2-factor interaction effect AGE*A/G (P=0.0176) is negatively associated with the DB. It implies that as the interaction effect (AGE*A/G) increases, DB decreases. Note that the marginal effect AGE (P=0.0371) is negatively, while A/G (P=0.0033) is positively associated with DB. Also the 2-factor interaction effects TB*ALP (P<0.0001), TB*SGPT (P<0.0001), ALP*A/G (P=0.1084) are negatively associated with the DB. It implies that as the above interaction effects increase, DB decreases. Note that the three marginal effects TB (P=0.9784), ALP (P=0.4374) and SGPT (P=0.8523) are insignificant, while A/G (P=0.0033) is positively associated with DB. Again, the 2-factor interaction effect TB*ALB (P<0.0001) is positively associated with the DB. Also the sex (male=0, female=1) is negatively associated with the mean direct bilirubin. It shows that DB is higher for male than female liver patients.
For the fitted variance model of direct bilirubin, types of patients (liver patient=1, non-liver patient=2) (CLUSTER) (P=0.0072) is negatively associated with DB variance, indicating that DB variance is higher for liver patients than non-liver patients. Also TP (P=0.0066) and A/G (P<0.0001) are negatively associated with the DB variance, indicating that DB variance increases as TP or A/G decreases. Again 2-factor interaction effects TB*ALP (P<0.0001) and AGE*SGOT (P=0.1226) are negatively associated with DB variance, indicating that DB variance increases as the joint effect of TB*ALP or AGE*SGOT decreases. Also 2-factor interaction effects TB*A/G (P<0.0001), ALP*SGPT (P=0.2694), and SGPT* ALB (P<0.0001) are positively associated with DB variance, indicating that DB variance increases as the joint effect of TB*A/G, or ALP*SGPT, or SGPT*ALB increases. Note that their marginal effects TB (P<0.0001), ALP (P=0.0003), SGPT (P<0.0001), SGOT (P=0.0921) and ALB (P=0.1653) are significantly associated with DB variance. All the above summarized relationships of the associated factors/ variables with direct bilirubin are shown in (Table 1).
The relationship of direct bilirubin with the other dependent variables and liver disease biochemical markers are displayed above (Table 1). The relationship of DB is very complicated, as the model contains many 2-factor and 3-factor interaction effects. To confirm that a patient is liver disease, all liver disease markers to be tested. Medical experts need to understand the role of different order of interaction effects of liver disease markers. Liver patients should be serious for the liver disease, as it is a very complicated.
References
- Stocker R, Yamamoto Y, McDonagh AF, Glazer AN, Ames BN (1987) Bilirubin is an antioxidant of possible physiological importance. Science 235(4792): 1043-1046.
- Baranano DE, Rao M, Ferris CD, Snyder SH (2002) Biliverdin reductase: a major physiologic cytoprotectant. Proc Natl Acad Sci USA 99(25): 16093-16098.
- Lin LY, Kuo HK, Hwang JJ, Lai LP, Chiang FT, et al. (2009) Serum bilirubin is inversely associated with insulin resistance and metabolic syndrome among children and adolescents. Atherosclerosis 203(2): 563-568.
- Tanaka M, Fukui M, Tomiyasu K, Akabame S, Nakano K, et al. (2009) Low serum bilirubin concentration is associated with coronary artery calcification (CAC). Atherosclerosis 206(1): 287-291.
- Cheriyath P, Gorrepati VS, Peters I, Nookala V, Murphy ME, et al. (2010) High total bilirubin as a protective factor for diabetes mellitus: an analysis of NHANES data from 1999-2006. J Clin Med Res 2(5): 201- 206.
- Ramana BV, Babu MSP, Venkateswarlu NB (2011) A critical study of selected classification algorithms for liver disease diagnosis. IJDMS 3(2): 101-114.
- Ramana BV, Babu MSP (2012) Liver classification using modified rotation forest. IJERD 1(6): 17-24.
- Das RN, Mukherjee S, Sharma I (2018) Alkaline Phosphatase determinants of liver patients. J Pancreas 19(1): 18-23.
- Lee Y, Nelder JA, Pawitan Y (2006) Generalized linear models with random effects (Unified Analysis via H-likelihood), Chapman & Hall, London, UK.
- Das RN, Lee Y (2009) Log normal versus gamma models for analyzing data from quality-improvement experiments. Quality Engineering 21(1): 79-87.
- Das RN, Park JS (2012) Discrepancy in regression estimates between Log-normal and Gamma: Some case studies. J Applied Statistics 39(1): 97-111.
- Das RN (2014) Robust response surfaces, regression, and positive data analyses. Chapman & Hall, London, UK.
- Nelder JA (1994) The statistics of linear models: back to basics. Statistics and Computing 4(4): 221-234.
- Das RN (2012) Discrepancy in fitting between log-normal and gamma models: An illustration. Model Assisted Statistics and Applications 7(1): 23-32.






























