Inferences on Treatment and Carryover Effects in Two-Period Two-Sequence Crossover Designs
Vladimir Geneus1, Chunming Li1, Sam Weerahandi1*, Ed Whalen1 and Ching Ray Yu2
1Department of Statistics, Florida State University, USA
2Department of Statistics, Pfizer Inc., USA
Submission: January 13, 2018; Published: February 01, 2018
*Corresponding author: Sam Weerahandi, Department of Statistics, Florida State University, 23 Chestnut St, Edison, NJ 08817, USA, Email: sweeraha@hotmail.com
How to cite this article: Vladimir G, Chunming L, S Weerahandi, E Whalen, Ching R Y. Inferences on Treatment and Carryover Effects in Two-Period Two-Sequence Crossover Designs. Curr Trends Biomedical Eng & Biosci. 2018; 11(5): 555821. DOI: 10.19080/CTBEB.2018.11.555821.
Abstract
It is well known that, in the absence of 4 sequences or a long washout period, it is not possible for classical methods to separate out the treatment effects and carryover effects of a crossover design involving two treatments. Motivated by self-contradictory, visually clear results from a standard mixed effects model repeated measures (MMRM) type analysis of a 2X2 crossover, we develop a method to take advantage of repeated measures in each period to make inferences on treatments and carryover effects. The proposed model applied to our data rectified the anomaly in our application. Results from a simulation study are also included to demonstrate the advantage of the proposed approach over the regular MMRM approach.
Introduction
The problem undertaken in this article was motivated by a real 2X2 crossover clinical trial of ours, in which classical analysis lead to counter intuitive results (see Figure 1), where the results before the crossover clearly shows that Treatment has performed better than the Placebo. Yet due to the absence of a long wash-out period or a four sequence, the crossover design has done more harm than good, when analyzed by classical methods. This is a situation that statisticians run into when clinicians conducting clinical studies frequently recommend crossover designs but due to inadequate funding they go ahead with the 2X2 design, leaving statisticians to figure things out. Having seen the issues from the post-crossover results that one can see from the figure, and having seen the widely used MMRM method failing to sort things out, in this article we propose how one can separate out the treatment effects and carryover effects by taking advantage the repeated measures. In fact, the proposed method can be applied even if there is no washout period.
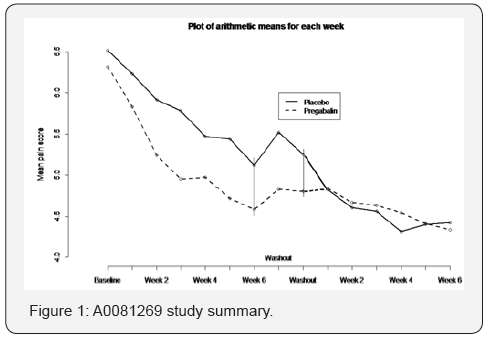
The underlying reason why the insignificant difference between the Treatment and Placebo suggested by MMRM was due to long carryover effect that did not adequately diminish during the washout period thus failing pain metrics to return to pre-trial levels. The application is discussed in greater detail in the following section.
Fleiss [1] describes in simple terms the well-known confounding of carryover and period effects in the two sequence, two treatments, two period crossover design (2X2 crossover). In this article we consider the case of the 2X2 crossover [2] when the dependent variable has repeated measures in each period. Weerahandi [3], Chapter 9, outlined the analysis of the 2X2 crossover and discussed the difficulties in trying to determine carryover effects, unless there is a fairly large washout period or if the carryover effects due to the two treatments are equal. In typical applications such assumptions are not reasonable, especially when a treatment is compared against a placebo. Moreover, long washout periods are not feasible prohibitive in type of application we discuss in the next section. The widely used approach to overcome such difficulties is to use four sequences to capture different carryover effects. Instead of the typical two sequences, say AB and BA, we can add two more sequences; say AA and BB, that have the same treatment in both periods (one sequence for each of the two treatments).
In some applications, as was the case in our application, it may be too expensive to have data from four sequences, or not considered acceptable at the design stage by non-statisticians, as was the case in our application. Some authors in this context argue that it is not possible separate out th carry over effects from treatment effects unless there are four sequence. This is not an acceptable answer when a study has been conducted using 2X2 crossover design at a large cost, and statisticians are asked to analyze the available data. In fact, the failure of classical methods to separate out confounding effects is not a fundamental flaw of the design, but rather it is a repercussion of inadequate modelling to take advantage of full information available from the data. The point is that, if the study involves repeated measures taken before and after the crossover, as usually the case, the data should allow us to compare treatments without the assumption of equal carryover effects, regardless whether or not there is a washout period. The literature provides [3] only ad hoc methods to model and analyze such repeated measures, and so the purpose of this article is to provide more formal development of a simple a model and develop inferences.
Since classical approaches to analyze 2X2 designs do not take full advantage of repeated measurements during each period, here we use the availability of within period repeated measures to model and estimate carryover effects by taking into account the active effect during each period. By expanding the model to handle both period and carryover effects, we can analyze data in which both effects exist and may differ between sequences and treatments. The reader is referred to Senn [4,5] and Jones & Kenward [6] for detailed discussions of underlying notions and available classical solutions in crossover designs.
Motivating example
The model and analysis developed in this article is motivated by a study of pain associated with diabetic peripheral neuropathy (pDPN). In the study, patients are randomized to one of two sequences and treated for six weeks in each of two treatment periods. Patients also go through a two week washout period between the two periods. Patients record their daily pain scores (an 11-point numeric rating scale from 0=no pain to 10=worst imaginable pain) which get combined into a weekly average pain score for each study week, including the washout weeks.
Figure 1 below displays the observed pain measures over the 14 weeks. Clearly the superiority of treatment (Pregabalin) over the Placebo in reducing the pain is clear from the first 6 weeks of data; while there is a high placebo effect as well, the separation of the two curves have increased over the weeks, except for noise. At the end of week 6 (period one) the difference has remained, roughly constant. But the crossover design seem to have done more harm than good, because during the two weeks of washout period of two weeks with no treatment, patients’ pain level has not gone back up to the baseline pain level. It is evident from evident from Figure 1; the two week washout period has not been long enough to allow the pain return to baseline pain level as demonstrated by the gap between the treatments at the end of the second washout week. The data observed after the washout period seem to be highly contaminated due to treatment effect confounding with the carryover effects.
In general, if an active treatment has modified the underlying pain mechanism for a subset of subjects, then no washout period will be long enough. In the traditional crossover literature, the crossover design is recommended. This provides no help when a study has been conducted to explore a new treatment for which any modifying effects are undiscovered prior to conducting the study.
Note however that the study yields repeated measurements throughout the 14 study weeks which can use to estimate of carryover effects in a manner different from the classical methods using individual measures from each period. Since the two sequences did not return to a common pain level at the end of the washout period, the traditional 2X2 crossover analyses run into difficulty. The sequence of active treatment followed by placebo (AB) has no appreciable return of pain and the placebo to active treatment (BA) sequence shows an initial slight return of pain but upon initiation of treatment continues a trend of pain improvement to the point where, for most of the second period, the two sequences show similar pain levels despite different treatments.
The rest of the article is organized as follows. Section 2 introduces the notation and the proposed new model to take advantage of repeated measures taken at each week. Section 3 shows results for the motivating study. Section 4 covers how to handle inferences. Section 5 applies the model and standard models to the example data. Section 6 presents the results of simulation studies. Section 7 discusses the implications of the model and further development opportunities. The authors have developed R programs for the proposed model, which are available upon request.
Two Sequence Crossover Design with Multiple Observations
Consider a two sequence crossover design with multiple observations, with a washout period as well. Let AB and BA be the two sequences (sometimes referred to as groups), say A is a treatment and B is the placebo.
2) At time periods t = T1+1, ..., T1+T, which is considered as the washout period, no treatment is administered.
3) At time periods t = T1 + τ + 1, ..., T1 + T2 + τ the observations are taken after crossover following the washout period while treating the patients with B and A, respectively at each time period.
For example, in our application T1 = T2 = 6 weeks and τ = 2 weeks. Assume that the mean effect of the treatment does not change over time. The treatment as well as the placebo each has a diminishing carryover, which is also known as decaying effect. Hence, when patients are treated in a given week, the carryover effects from prior week’s needs to be taken into account.
Proposed model
The literature on crossover designs does not provide a model to take ad- vantage of such repeated measures to separate out the treatment effects and carryover effects. Therefore, in this section we develop a simple model having some desirable properties, including the most desirable property that when a patient has been on therapy for a while, then he/she will get the full effect of the treatment in a period (e.g. day, week), regardless of the extent of accumulated carryover effects. This property will be further described below. We accomplish this by capturing the carryover effects from prior periods and the effect of the latest treatment. To describe how to capture carryover effects, suppose one therapy of a treatment has a full mean effect of magnitude δ when the patient has been on constant therapy for a while until full effect of the treatment is realized. It should be emphasized that is not an assumption, but rather a well defined quantity that is used in analyses not involving crossover designs as well. When the patients are treated number of times (eg. daily), ρ represents the mean pain reduction over the period when the patient has been on recommended therapy and dosage. Suppose, when a patient get started on the therapy the effective fraction of δ, in the first period is ρ and the fraction of its carryover for future periods is 1- ρ, where 0 < ρ < 1. This means that active treatment effects of one therapy at periods t= 1, 2, 3, ... are δ1 = ρδ, δ2 = (1- ρ)ρδ, δ3 = (1- ρ)2ρδ..., which all add up exactly to δ, a well known property of the geometric series, thus implying that δ is indeed the total effect from one therapy if the patient had been on therapy for a long time. It should be noted that the assumption of additivity of effects is the same as the one used in traditional crossover models with four sequences, and so only new assumptions here are that the rate at which active effect diminishes over time is multiplicative and that the ρ parameter is constant over time.
Noting that δt= (1-ρ)δt-1, if a patient has been continuously undergoing the same treatment for n periods, then the full effect of current treatment and all carryover effects at time n, say μn, can be computed explicitly as

again using the geometric series summation formula. Formula (2) implies three important and highly desirable properties of the model, namely, if a patient keeps taking the treatment every period, then
1) The active effect at period n, namely μn is an increasing function of n,
2) μn never exceeds the full effect of one therapy, δ
3) As n → ∞, μn → δ, a highly desirable conditions that few models can provide, because it implies that after the patient has been continuously under therapy, the patient will tend to get the full effect of one therapy within the period.
Another useful property that follows from (1) is that the full effect of current treatment and all carryover effects, μn can simply be expressed in terms of the effect of current treatment and the full effect during the previous treatment; i.e.
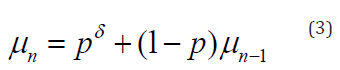
Where (1−ρ)μn−1 is the accumulated carryover effects from prior periods.
Now we are in a position to express active mean effects throughout the crossover experiment. To do so, let the total mean effect when all decaying effects are accounted for be denoted as

Where c is the treatment given to a certain patient, which depends on time t.
Let ρA and ρB be the decay rates of the two treatments A and B, respectively.
Using t1 notation to denote lagged effects at period (t−1) and letting s to denote lagged effect at (t−T1+τ), now we can express mean effect of AB group at any time period t, including the washout period, as
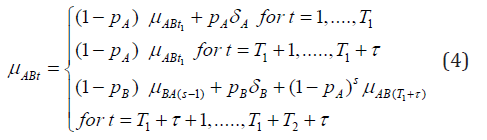
Similarly for the BA group, we can express the mean effect at any time period as
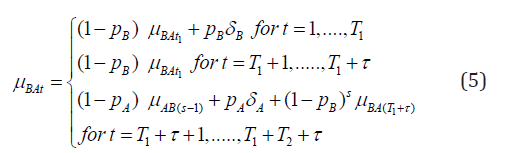
Equations (4) and (5) allow us to express all mean effects in terms of the four parameters δA, δB, ρA, ρB as we will further clarify in the next section. Let Yijt denote the response of ith subject of jth sequence taken at time period t. Then assuming a linear model, we get
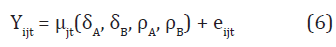
Where j = AB, BA; i = 1, ..., I; t = 1..., 2T + τ and eijt are the residuals, which we assume to be normally distributed. Since we are dealing with situation of repeated measures, depending on whether or not there are a large number of subjects, the covariance structure of the residual error terms is best handled by an unstructured covariance matrix, or by a compound symmetric covariance structure with two variance components representing the among subject and within subject variance.
Reduced Model as Used in Application
Equations (4) and (5) involve recursive formulas, which is not very convenient in practice. It is desirable to express the mean function in terms of the four unknown parameters involving no recursive formula, which vary only with the sequence and the period. Indeed, it is possible to express the mean function without recursive formulas. To see this let us first consider our application, where T1 = T2 = 6 and τ = 2, first note that it follows from (4) that

Moreover, it also follows from (??) that

and that

It is now clear that, in general for any number of repeated measures, we can express (4) as
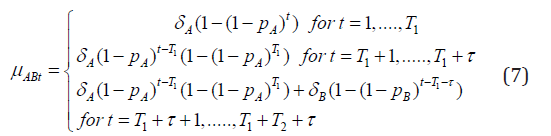
Similarly we can express μBAt as a non-linear function of the four unknown parameters by changing the role of A and B. The model established in this manner will be referred to as the “Rho Model”.
Inference
Note that the above model is linear in all parameters of interest, but is non-linear with respect to the nuisance parameters ρA and ρB. Since we are dealing with repeated measures, one should be able to make inferences about all parameters in a nonlinear mixed model setting with compound symmetric structure, which is adequate in typical applications. Then, the parameter estimation and other inferences such as testing can be carried out using widely used software solutions such as SAS nlmixed or R nlme.
The estimated model allows us to compare overall effect of each treatment or at the end of each phase of the study. For example in our application, the contrast of interest is δA−δB for the former. More importantly, inferences on differences in means effects at end points can be based on formulas

and

The problem of making inferences on model parameters can also be accomplished by iterative linear mixed model applications. This is possible because the model is linear in parameters of interest, and is non-linear only with respect to the nuisance parameters ρA and ρB. This is accomplished in the following steps:
1) Start with some initial values of ρA and ρB, such as 0.5 each,
2) When the nuisance parameters are specified, carry out the analysis of the model in a single linear mixed model setting,
3) Obtain the error sum of squares,
4) Repeat above steps in an iterative manner until the error sum of square is minimized,
5) Obtain the values of ρA and ρB that achieve the minimum error sum of squares, and run the final linear mixed model to perform inferences on parameters of interest.
Results from the Proposed Model and Comparison to Standard Models
Diabetic peripheral neuropathy (DPN) is one of the most common complications affecting patients with diabetes. DPN is often asymptomatic, but when symptoms do appear, they include numbness, weakness, tingling, or pain. Painful DPN can impact patients’ ability to walk or perform daily activities.
The study from the motivating example in Section 1 was a randomized, double-blind, placebo-controlled, multi center, 2x2 crossover study and con- ducted at 36 centers in the United States, Czech Republic, South Africa, and Sweden (Clinical Trials gov: NCT01474772). Patients aged 18 or older were randomized to one of the two treatment sequences: pregabalin followed by placebo, or placebo followed by pregabalin, respectively. Within each sequence, there were two double-blind periods of 6 weeks each, and between the two periods, there was a 2-week washout period. Results of the study are published elsewhere by Huffman et al. [7].
A total of 205 patients with painful DPN were randomized and assigned to a treatment sequence. Two patients were randomized but discontinued before receiving study medication. Of the 203 patients that were treated, 101 patients were assigned to the pregabalin→placebo treatment sequence and 102 patients to the placebo→pregabalin treatment sequence. Among those treated, 77 (76.2%) completed treatment required by protocol in the pregabalin→placebo sequence while 87 (85.3%) completed in the other sequence. The demographic and baseline clinical characteristics were comparable between the 2 treatment sequences.
In the pre-specified analysis plan, the endpoint DPN pain was analyzed using a linear mixed-effects model, including baseline pain, sequence, period, center, and treatment as fixed effect factors, and subject within sequence and within-subject error as random factors. The treatment difference (pregabalinplacebo) was tested using within-subject variability as the error term. Analysis was implemented using SAS Proc Mixed to handle the repeated measures. Based on the pre-specified analysis, the treatment difference was not statistically significant at 0.05 alpha levels. However, there was evidence that a carryover and/ or a treatment-by-period interaction effect were significant (p < 0.05). As also shown, the second baseline prior to the second period was different between the two sequences while it did not return to the original baseline in either sequence.
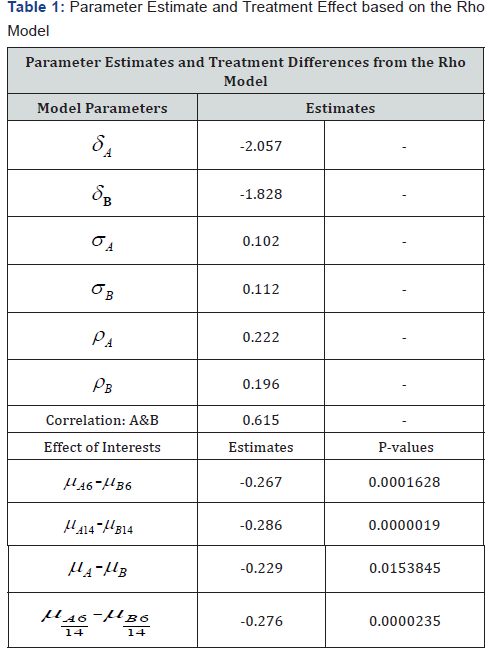
The following Tables 1 & 2 display results for the proposed Rho model and the MMRM model. The primary interest is in the combined end of period treatment estimates and their comparison (i.e. Week 6/14 in the tables).
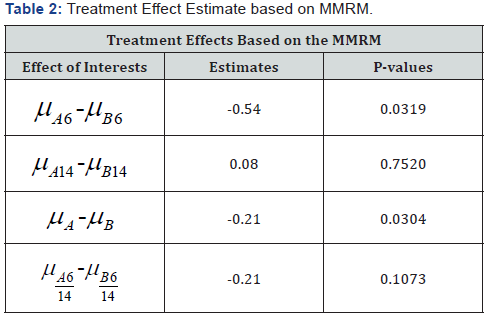
Table 2 displays the results from the MMRM model for comparison with the Rho model in Table 1. Estimated treatment differences for the combined week 6/14 time-point show a smaller difference with MMRM. The Rho model has a larger difference. With respect to statistical significance, the Rho model has a p-value p < 0.0001 compared with a non-significance for the MMRM model.
The preceding results suggests that the Rho model has greater power than the traditional MMRM and a standard one measure period result such as in the primary analysis of the study. To further understand the power performance we compared the competing models using simulated data sets. The key parameters for the simulated data sets are the correlation structure and the mean pain vectors for each treatment. We simulated these assuming a multivariate normal (MVN) distribution of dimension 14, one for each study week. The MVN parameters used in the simulation studies were based on the observed ones from the example study.
Simulation Study
Since competing procedures do not assume the same model, the purpose of this simulation is not a proof that the proposed model is superior, but rather to provide some idea about at what level of carryover effects, we can use the simple MMRM and when to use alternative models such as the proposed model.We carried out the simulation study to compare the bias and the mean square error(MSE) of the proposed model against regular MMRM approach, under scenarios of the treatment effects δA and δB and nuisance parameters ρA and ρB and sample size nAB and nBA. The case of equal sample size set at 50 is mostly studied, and the case of nAB is larger is briefly studied to understand the results when more emphasis is placed on the pre-washout period. In our study of performance of proposed method compared with the widely used MMRM method (by practitioners) is carried out by generating data as follows:
1) We assumed T1 = 6, τ = 2 and T2 = 6 with total 14 weeks of the evaluation duration.
2) Given pre-specified overall effect δA, δB and the nuisance parameters carryover effect ρA, ρB, from (5) and (6), the treatment effect μABt and μBAt at week t, t = 1, . . . , 14 can be calculated.
3) For each week t, nAB, nBA data points were generated from normally distributed with mean μABt + ν AB and μBAt + ν BA and standard deviation σE= 0.5, where νAB, νBA were normally distributed with mean 0 and standard deviation σAB, σBA, respectively.
Parameter estimation
1) For each Monte Carlo (MC) iteration, data points were generated and both MMRM and new model were applied to get the estimates of δA and δB.
2) From the equation (5), we got μAB6 and μBA6 from outputs of both model.
3) The bias and MSE were calculated for MC = 1000.
Findings
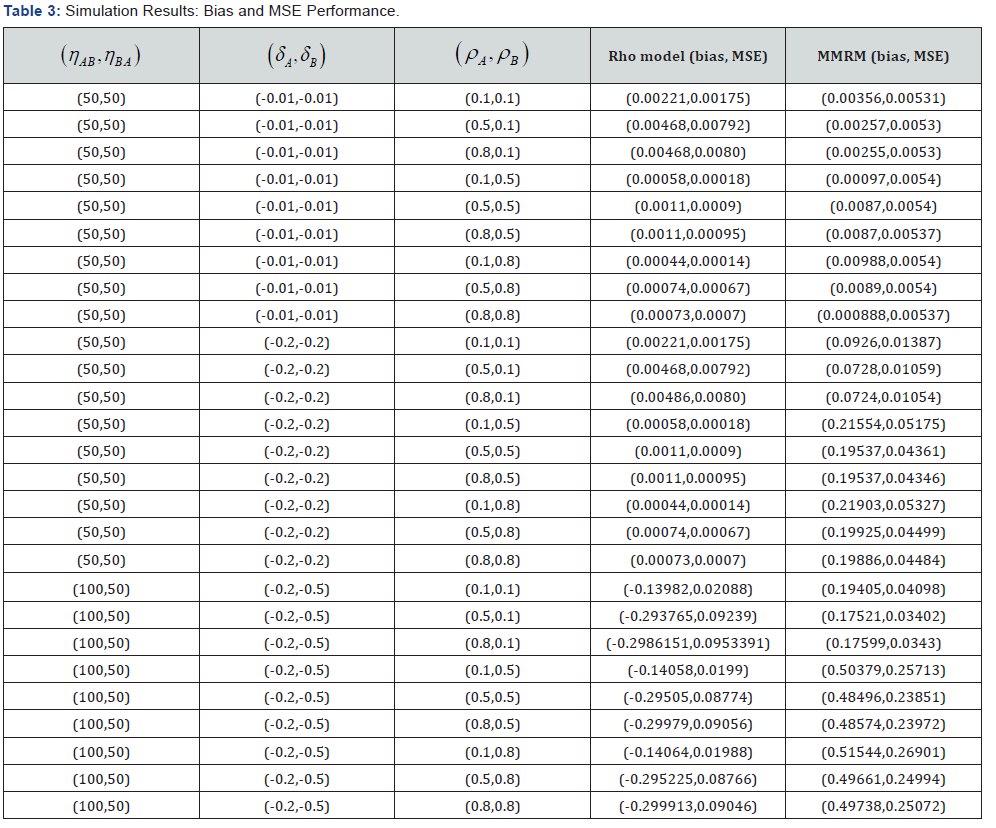
The results of the simulated study are displayed in the Table 3. The table shows the bias and the MSE (mean squared error) due to MMRM and the proposed model. It is evident from Table 3 that the proposed model has led to estimates with smaller absolute bias as well as MSE. When ρA and ρB are large, the improvement was found to be substantial. When δ values are large the MSE of each method tend to go up, as expected.
Discussion
In this article we have established that in the absence of four sequences we can quantify the carryover effects by modelling the active treatment mean and carryover effects, under the simple assumption that the decay factors remain roughly constant over time. In our application the assumption yielded reasonable results when we studied results before the crossover and the washout period. Further research is encouraged to extend results under alternative assumptions.
In general, not only the carryover effects, but also decay factors may vary overtime. This is a problem beyond the scope of this article, so we encourage further research in this direction. Decay effects that may diminish or increases over time might be of particular interest.
In this article introducing a satisfactory solution to two sequence crossover designs, we have not developed inference methods for the ρ parameters, be- yond the point estimation. This is also an area requiring further research.
One may also take non-parametric approach to tackle the carryover effects. While such an approach has the advantage of being based on fewer assumptions, it may tend to yield less power in detecting truly significant results of experiments.
One may also take non-parametric approach to tackle the carryover effects. While such an approach has the advantage of being based on fewer assumptions, it may tend to yield less power in detecting truly significant results of experiments.
In our application, the week 14 treatment difference estimate for the Rho model is -0.29 versus 0.08 for MMRM. Estimates of the week 6/14 (end of period) treatment difference also tended to be smaller for the MMRM com- pared to the other two models. The results on statistical significance suggest that the Rho model may have advantages over the other two models. The decay factor alleviates the tendency of models such as the traditional single measure per period and MMRM analyses to diminish the estimated differences in later periods as a result of their inflexible assumptions on carryover effects.
In our application we used the REML method to estimate parameters in a Mixed Model setting. It is well known that MLE based methods, such as REML and ML, available from widely used software packages are based on asymptotic methods. When the sample size is small one may take the generalized inference [9] approach to tackle the model parameters.
References
- Fleiss JL (1989) A critique of recent research on the two-treatment crossover design. Control Clin Trials 10(3): 237-243.
- Balaam LN (1968) Two-period design with t2 experimental units. Biometrics 24(1): 61-73.
- Weerahandi S (2004) Generalized inference in repeated measures: exact methods in MANOVA and mixed models. Wiley, Hoboken, New Jersey, USA.
- Senn SJ (2002) Cross-over trials in clinical research. (2nd edn), Wiley, Chichester, England, UK.
- Senn SJ (2006) Cross-over trials in statistics in medicine: the first ‘25’ years. Stat Med 25(20): 3430-3442.
- Jones B, Kenward MG (2014) Design and analysis of cross-over trials. (3rd edn), CRC Press, Boca Raton, Florida, USA.
- Huffman C, Stacey BR, Tuchman M, Burbridge C, Li C, et al. (2015) Efficacy and safety of pregabalin in the treatment of patients with painful diabetic peripheral neuropathy and pain on walking. Clin J Pain 31(11): 946-958.
- Kenward MG, Roger JH (1997) Small sample inference for fixed effects from restricted maximum likelihood. Biometrics 53(3): 983-997.
- Tsui K, Weerahandi S (1989) Generalized p-values in significance testing of hypotheses in the presence of nuisance parameters. JSTOR 84(406): 602-607.






























