Unraveling the Collective Dynamics of Complex Adaptive Biomedical Systems
D Dylan Johnson Restrepo and Neil F Johnson*
Physics Department, University of Miami, USA
Submission: May 02, 2017; Published: September 07, 2017
*Corresponding author: Neil F Johnson, Physics Department, University of Miami, USA, Email; neiljohnson@miami.edu
How to cite this article: D Dylan J Restrepo, N F Johnson. Unraveling the Collective Dynamics of Complex Adaptive Biomedical Systems. Curr Trends Biomedical Eng & Biosci. 2017; 8(5): 555749. DOI: 10.19080/CTBEB.2017.08.555749
Abstract
Many systems in Biomedical Engineering and across the Biosciences involve collections of semi-autonomous objects which may be naturally occurring or artificial (e.g, nanostructures or nanomachines). Such collections of objects do not typically have any central controller, and yet respond to the same global cues in terms of feedback of information from the environment. They also typically will not be inert or identical. Instead they are heterogenous and may respond differently to a given piece of external information or system history according to the particular state that they are in, meaning that have effectively have a limited set of simple strategies. In this mini-review, we outline an approach to tackling the general challenge of understanding how collections of such heterogeneous, adaptive systems behave dynamically. These issues are important for understanding the inherent risks involved in the collective behavior of next-generation systems of objects ('agents') across the spectrum of biomedical engineering applications.
Introduction
Whether natural or artificially made, biomedical systems involving large collections of semi-autonomous objects cannot easily be controlled in a centralized way because of the large overhead of required resources, as well as the risk of losing that central control to an outside attacker. There is therefore a pressing need in the biomedical sciences held to understand the fluctuations of such systems at the global level, in order to guide the design of next-generation collections of natural, artificial or hybrid objects in the setting of biomedical engineering and bioscience systems.
A common feature of such systems is that they involve collections of objects with the following features:
a) Many interacting agents: The system contains many components or participants, known as 'agents, which interact in possibly time-dependent ways. Their individual behavior will respond to the feedback of information, which is possibly limited, from the system as a whole and/ or from other agents. Since these agents may effectively be competing to win, it is unlikely that there is any such thing as a 'typical agent.
b) Evolution: The en-tire multi-agent population evolves, driven by an ecology of agents who interact and adapt under the influence of feedback. The system typically remains far from equilibrium and hence can exhibit extreme behavior.
c) Single realization: The system under study is a single realization, implying that standard techniques whereby aver-ages over time are equated to averages over ensembles, may not work.
d) Open system: The system is coupled to the environment, hence it is hard to distinguish between exogenous (i.e. outside) and endogenous (i.e. internal, selfgenerated) effects.
e) Feedback: The nature of the feedback can change with time {for example, becoming positive one moment and negative the next. They may also change in magnitude and importance. It may also operate at the macroscopic or microscopic level, or both. The presence of feedback implies that on some level, buried in the details of the dynamics, the system re-members its past and responding to it, albeit in a highly non-trivial way.
f) Non-stationarity: We cannot assume that the dynamical or statistical properties observed in the systems past, will remain unchanged in the systems future.
g) Adaptation: An agent can adapt its behavior in the hope of improving its performance.
In this short paper, we outline an approach to understanding the behavior of such systems and their likely dynamical behaviors. Our focus is on understanding how their heterogeneity and limited decision-making ability (i.e. limited number of simple effective strategies) combine with their access to common global information, to generate system fluctuations. Such fluctuations may create harm for the system and so it is important to under-stand how they are generated, their typical size, and how they depend on the system parameters.
Complex systems background
Complex Systems, which exhibit dynamical behavior known as Complexity, pervade much of the natural, social and technological world [1-8]. There is no unique, all-encompassing definition of a Complex Sys-tem, so they are better thought of in terms of the list of their common features: feedback and adaptation at the macroscopic and/or microscopic level, many (but not too many) interacting parts, non-stationarity, evolution, coupling with the environment, and observed dynamics which depend upon the particular realization of the system. Complex Systems have the ability to produce large macroscopic changes which appear spontaneously but have long-lasting consequences, which can be referred to as 'punctuated equilibria' depending on the context [9]. The particular trajectory taken by a Complex Sys-tem can be thought of as exhibiting 'frozen accidents' [9,10]. John Casti pointed out on p. 213 of Ref. [4], a decent mathematical formalism to describe and analyze the [so-called] El Farol Problem would go a long way toward the creation of a viable theory of complex, adaptive systems'. The rationale behind this statement is that the El Farol Problem, which was originally pro-posed by Brian Arthur [11] to demonstrate the essence of complexity in financial markets, incorporates the key features of a complex system in a readily understandable setting. The El Farol Problem concerns the collective decision-making of a group of potential bar-goers, who repeatedly try to predict whether they should attend a potentially overcrowded bar on a given night each week. They have no information about the others predictions. Indeed the only information available to each agent is global, comprising a string of outcomes ('overcrowded' or 'undercrowded') for a limited number of previous occasions. Hence they end up having to predict the predictions of others. No 'typical' agent exists, since all such typical agents would then make the same decision, hence rendering their common prediction scheme useless. This simple yet intriguing problem has inspired a huge amount of interest in the physics community over the past few years [12], which was the rst work on the full El Farol Problem in the physics community, identified a minimum in the volatility of attendance at the bar with increasing adaptivity of the agents. With the exception of [12], the physics literature has instead focused on a simplified binary form of the El Farol Problem as introduced by Challet & Zhang [13]. This so-called Minority Game (MG) is discussed in detail in Refs. [14-41] and [42]. The Minority Game concerns a population of N heterogeneous agents with limited capabilities and information, who repeatedly compete to be in the minor-ity group. The agents (e.g. people, cells, data-packets) are adaptive, but only have access to global information about the game's progress. In both the El Farol Problem and the Minority Game, the time-averaged fluctuations in the system’s global output are of particular importance { for example, the time-averaged fluctuations in attendance can be used to assess the wastage of the underlying global resource (i.e. bar seating).
Before progressing to understand this model, we acknowledge that of course the El Farol Problem (and the Minority Game in particular) has the following shortfalls: First, the reward structure is simultaneously too restrictive and specific. Agents in the Minority Game, for example, can only win if they instantaneously choose the minority group at a particular time step: yet this is not what investors in a financial market, for example, would call 'winning' [43]. Second, agents only have access to global information. In the natural world, most if not all biological and social systems have at least some degree of underlying connectivity between the agents, allowing for local exchange of information or physical goods [44]. In fact it is this interplay of network structure, agent het-erogeneity, and the resulting functionality of the overall system, which is likely to be of prime interest across disciplines in the Complex Systems.
Crowd-anticrowd framework
We here outline a crowd-based approach describing the dynamics of a complex multi-agent system, which incorporates accurately the correlations in strategies followed by the agents. The Crowd-Anti crowd analysis breaks the N-agent population down into groups of agents, accord-ing to the correlations between these agents' strategies. Each group G contains a crowd of agents using strategies which are positively-correlated, and a complementary anti crowd using strategies which are strongly negatively-correlated to the crowd. Hence a given group G might contain nR[t] agents who are all using strategy R and hence act as a crowd (e.g. by attending the bar en masse in the El Farol Problem) together with nR[t] agents who are all using the opposite strategy R and hence act as an anticrowd (e.g. by staying away from the bar en masse). Most importantly, the anti crowd nR[t] will always take the opposite decisions to the crowd nR[t] regardless of the current circumstances in the game, since the strategies R and R imply the opposite action in all situations. Note that this collective action may be entirely involuntary in the sense that typical games will be competitive, and there may be very limited (if any) communication between agents. Since all the strong correlations have been accounted for within each group, these individual groups {G} = G1 G2, . . . ,Gn. will then act in an uncorrelated way with respect to each other, and hence can be treated as n uncorrelated stochastic processes. The global dynamics of the system is then given by the sum of the n uncorrelated stochastic processes generated by the groups {G} = G1 , G2 , . . . ,Gn . There have been various alternative theories proposed to describe the MG’s dynamics [15-19,21,37,38,40,41]. Although elegant and sophisticated, such theories have however not been able to reproduce the original numerical results of Ref. [23] over the full range of parameter space. What is missing from such theories is an accurate description of the correlations between agents' strategies: in essence, these correlations produce a highly-correlated form of decision noise which cannot easily be averaged over or added in. By contrast these strong correlations take center-stage in the Crowd-Anticrowd theory, in a similar way to particle-particle correlations taking centerstage in many-body physics.
B-A-R (Binary Agent Resource) systems
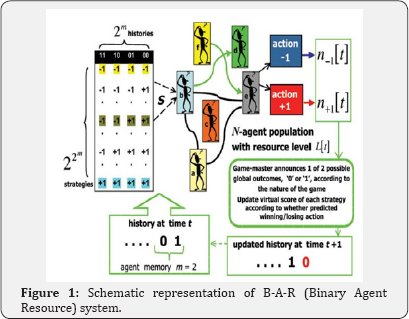
Figure 1 summarizes the generic form of the B-A-R (Binary Agent Resource) system under consideration. At time step t, each agent (e.g. a bar customer, a commuter, or a market agent) decides whether to enter a game where the choices are action +1 (e.g. attend the bar, take route A, or buy) and action 1 (e.g. go home, take route B, or sell). We will denote the number of agents choosing 1 as n-1[t], and the number choosing +1 as n+1[t]. For simplicity, we will assume here that all the agents participate in the game at each time step, although this is not a necessary restriction. We can de ne an 'excess demand' as
D[t] = n+1[t]-n-1[t]: (1)
As suggested in Figure 1, the agents may have connections between them: these connections may be temporary or permanent, and their functionality may be conditional on some other features in the problem. The global information available to the agents is a common memory of the recent history, i.e. the most recent m global out-comes. For example for m=2, the possible forms are: ...00,...01,...10 or ."11 which we denote simply as 00, 01, 10 or 11. Hence at each time step, the recent history constitutes a particular bit-string of length m. For general m, there will be P =2m possible history bit-strings. These history bit-strings can alternatively be represented in decimal form: μ= {0,1,...,P-1} where μ=0 corresponds to 00, μ=1 corresponds to 01 etc. A strategy consists of a predicted action, 1 or +1, for each possible history bit-string. Hence there are 2P possible strategies. For m =2 for example, there are therefore 16 possible strategies. In order to mimic the heterogeneity in the system, a typical game setup would have each agent randomly picking S strategies at the outset of the game. In the Minority Game, these strategies are then fixed for all time -however a more general setup would allow the strategies held, and hence the heterogeneity in the population, to change with time. The agents then update the scores of their strategies after each time step with +1 (or 1) as the pay-o for predicting the action which won (or lost). This binary representation of histories and strategies is due to Challet & Zhang [14].
The dynamics are determined by the rules of the game. The particular rules chosen will depend on the practical system under consideration. It is an open question as to how best to abstract an appropriate 'game' from a real-world Complex System [43,44], we discuss multi-agent games which are relevant to financial markets. Elsewhere we plan to discuss possible choices of game for the specific case of for aging fungal colonies [45]. The foraging mechanism adopted within such net-works might well be active in other biological systems, and may also prove relevant to social/economic networks. Insight into network functionality may even prove useful in designing and controlling arrays of imperfect nano structures, microchips, nano-bio components, and other 'systems on a chip' [46].
The following rules need to be specified in order to fully de ne the dynamics of a multi-agent game: Figure 1. Schematic representation of B-A-R (Binary Agent Resource) system. At time step t, each agent decides between action 1 and action +1 based on the predictions of the S strategies that he possesses. A total of n-1[t] agents choose 1 and n+1[t] choose +1. In the simplified case that each gent's confidence threshold for entry into the game is very small, Figthenl n-1[t] + n+1[t] = N (i.e. all agents play at every time step). Agents may be subject to some underlying net-work structure which may be static or evolving, and ordered or disordered. The strategy allocation, and hence heterogeneity in the population, provides a further source of disorder which may be static (i.e. quenched) or evolving. The algorithm for deciding the global outcome, and hence which action was winning/losing, lies in the hands of a ficticious 'Game-master'. This Game-master aggregates the agents' actions and then announces the global outcome. All strategies are then rewarded/penalized according to whether they had predicted the winning/losing action.
How is the global outcome, and hence the winning action, to be decided at each time step t? In a general game, the global outcome may be an arbitrary function of the values of n-1[t'≤t], n+1[t'≤t], and L[t'≤t] for any t’. Consider the specific case of the El Farol Problem: we can de ne the action +1 (1) to be attend (stay away) with L[t] representing the bar capacity. If n+1[t] <L[t], the bar will be under crowded and hence can be assigned the global outcome 0. Hence the winning action is +1 (i.e. attend). Likewise if n+1[t] > L[t], the bar will be overcrowded and can be assigned the global outcome 1. The winning action is then 1 (i.e. stay away). However more generally, the global out-come and hence winning action may be any function of present or past system data. Furthermore, the resource level L[t] may be endogenously produced (e.g. a specific function of past values of n-1[t], n+1[t]) or exogenously produced (e.g. deter-mined by external environmental concerns). Figure 1 denotes the global outcome (and hence winning action) algorithm as lying in the hands of a fictitious 'Game-master’, who aggregates the information in the game such as n+1[t], n-1[t] and L[t], and then announces the global outcome. We note that in principle, the agents themselves do not actually need to know what game they are playing. Instead they are just fed with the global outcome: each of their S strategies are then rewarded/penalized ac-cording to whether the strategy predicted the winning/losing action. One typical setup has agents adding/deducting one virtual point from strategies that would have suggested the winning/losing action.
How do agents decide which strategy to use? Typically one might expect agents to play their highest scoring strategy, as in the original El Farol Problem and Minority Game. However agents may in-stead adopt a stochastic method for choosing which strategy to use at each time step. There may even be 'dumb' agents, who use their worst strategy at each time step. Of course, it is not obvious that such agents would then necessarily lose, i.e. whether such a method is actually dumb will depend on the decisions of the other agents.
What happens in a strategy tie-break situation? Suppose agents are programmed to always use their highest-scoring strategy. If an agent were then to hold two or more strategies that are tied for the position of highest-scoring strategy, then a rule must be invoked for breaking this tie. One example would be for the agent to toss a fair coin in order to decide which of his tied strategies to use at that turn of the game. Alternatively, an agent may prefer to stick with the strategy which was higher on the previous time step.
What are the rules governing the connections between agents? In terms of structure, the connections may be hard-wired or temporary, random or ordered or partially ordered (e.g. scalefree network or small-world network). In terms of functionality, there is also an endless set of possible choices of rules. For example, any two connected agents might compare the scores of their highest scoring strategies, and hence adopt the predicted action of whichever strategy is overall the highest-scoring. Just as above, a tie-break rule will then have to be imposed for the case where two connected agents have equal-scoring highest strategies - for example a coin-toss might be invoked, or a 'selfish' rule may be used whereby an agent sticks with his own strategy in the event of such a tie. The connections themselves may have directionality, e.g. perhaps agent b can influence agent d but not vice-versa. Or maybe the connection (e.g. between b and a) is inactive unless a certain criterion is met. Hence it may turn out that agent b follows d even though agent d is actually following agent a.
Do agents have to play at each time step? For simplicity in the present paper, we will consider that this is the case. This rule is easily generalized by introducing a confidence level: if the agent doesn't hold any strategies with sufficiently high success rate, then the agent does not participate at that time step. This in turn implies that the number of agents participating at each time step fluctuates. We do not pursue this generalization here, but note that its effect is to systematically prevent the playing of low-scoring strategies which are anti-correlated to the high- scoring strategies. For financial markets, for example, this extra property of confidence level is a crucial ingredient for building a realistic market model, since it leads to fluctuations in the 'volume' of active agents [35,43].
We emphasize that the set-up in Figure 1 does not make any assumptions about the actual game being played, nor how the winning decision is to be decided. Instead, one hopes to obtain a fairly general description of the type of dynamics which are possible without having to specify the exact details of the game. On the other hand, situations can arise where the precise details of the strategy tie-break mechanism, for example, have a fundamental impact on the type of dynamics exhibited by the system and hence its overall performance in terms of achieving some particular goal. We refer to [43-47] for an explicit example of this, for the case of network-based multi-agent systems.
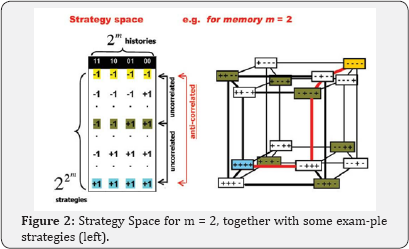
Figure 2 shows in more detail the m=2 example strategy space from Figure 1. A strategy is a set of instructions to describe what an agent should do in any given situation, i.e. given any particular history μ, the strategy then decides what action the agent should take. The strategy space is the set of strategies from which agents are allocated their strategies. If this strategy allocation is fixed randomly at the outset, then this acts as a source of quenched disorder. Alternatively, the strategy allocation may be allowed to evolve in response to the system’s dynamics. In the case that the initial strategy allocation is fixed, it is clear that the agents playing the game are limited, and hence may become 'frustrated', by this quenched disorder. The strategy space shown is known as the Full Strategy Space FSS, and contains all possible permutations of the actions 1 and +1 for each history. As such there are 22m strategies in this space. The 2m dimensional hypercube shows all 22m strategies from the FSS at its vertices. Of course, there are many additional strategies that could be thought of, but which aren’t present within the FSS. For example, the simple strategies of persistence and anti-persistence are not present in the FSS. The advantage however of using the FSS is that the strategies form a complete set, and as such the FSS displays no bias towards any particular action for a given history. To include any additional strategies like persistence and anti-persistence would mean opening up the strategy space, hence losing the simplicity of the B-A-R structure and returning to the complexity of Arthur's original El Farol Problem [11,12].
Figure 2 Strategy Space for m=2, together with some example strategies (left). The strategy space shown is known as the Full Strategy Space FSS, and contains all possible permutations of the actions 1 and +1 for each history. There are 22m strategies in the FSS. The 2m dimensional hypercube (right) shows all 22m strategies from the FSS at its vertices. The shaded strategies form a Reduced Strategy Space RSS. There are 2.2m = 2m+1 strategies in the RSS. The red shaded line connects two strategies with a Hamming distance separation of 4 [43].
It can be observed from the FSS, that one can choose a subset of strategies [14] such that any pair within this subset has one of the following characteristics: anti-correlated, e.g. -1 -1 -1 -1 and +1+1+1+1, or +1 +1 + 1 + 1 and +1 + 1 +1 +1. For example, any two agents using the (m =2) strategies +1 +1 + 1 + 1 and +1 + 1 +1 +1 respectively, would take the opposite action irrespective of the sequence of previous outcomes and hence the history. Hence one agent will always do the opposite of the other agent. For example, if one agent chooses +1 at a given time step, the other agent will choose 1. Their net effect on the demand D[t] therefore cancels out at each time step, regardless of the history. Hence they will not contribute to fluctuations in D[t]. uncorrelated, e.g. -1 -1 -1 -1 and 1 1 + 1 + 1. For example, any two agents using the strategies -1 -1 -1 -1 and +1 +1 + 1 + 1 respectively, would take the opposite action for two of the four histories, while they would take the same action for the remaining two histories. If the m =2 histories occur equally often, the actions of the two agents will be uncorrelated on average.
A convenient measure of the distance (i.e. closeness) of any two strategies is the Hamming distance which is defined as the number of bits that need to be changed in going from one strategy to another. For example, the Hamming distance between -1-1-11 and +1 + 1 + 1 + 1 is 4, while the Hamming distance between -1-1-1-1 and 1+ 1 + 1 + 1 is just 2. Although there are 2P ≡22m=2 ≡ 16 strategies in the m =2 strategy space, it can be seen that one can choose subsets such that any strategy-pair within this subset is either anti-correlated or uncorrelated. Consider, for example, the two groups

Any two strategies within Um=2 are uncorrelated since they have a Hamming distance of 2. Likewise any two strategies within Um=2 are uncorrelated since they have a relative Hamming distance of 2. However, each strategy in Um=2 has an anti-correlated strategy in Um=2: for example, -1 -1 -1 -1 is anticorrelated to +1+1+1+1, +1 + 1-1 -1 is anticorrelated to +1 +1 +1 +1 etc.
This subset of strategies comprising Um=2 and Um=2, forms a Reduced Strategy Space (RSS) [14]. Since it contains the essential correlations of the Full Strategy Space (FSS), running a given game simulation within the RSS is likely to reproduce the main features obtained using the FSS [14]. The RSS has a smaller number of strategies 2.2m = 2P= 2m+1 than the FSS which has 2P = 22m. For m =2, there are 8 strategies in the RSS compared to 16 in the FSS, whilst for m = 8 there are 1:16 1077 strategies in the FSS but only 512 strategies in the RSS. We note that the choice of the RSS is not unique, i.e. within a given FSS there are many possible choices for a RSS. In particular, it is possible to create 22m =2m+1 distinct reduced strategy spaces from the FSS. In short, the RSS provides a minimal set of strategies which 'span' the FSS and are hence representative of its full structure.
The history μ of recent outcomes changes in time, i.e. it is a dynamical variable. The history dynamics can be represented on a directed graph (a so-called digraph). The particular form of directed graph is called a de Bruijn graph. Figure 3 shows some examples of the de Bruijn graph for m = 1, 2, and 3. The probability that the out-come at time t + 1 will be a 1 (or 0) depends on the state at time t. Hence it will depend on the previous m outcomes, i.e. it depends on the particular state of the history bit-string. The dependence on earlier time steps means that the game is not Markovian. However, modifying the game such that there is a nite time-horizon for scoring strategies, may then allow the resulting game to be viewed as a high-dimensional Markov process [32,33] for the case of the Minority Game.

The dynamics for a particular run of the B-A-R sys-tem will depend upon the strategies that the agents hold, and the random process used to decide tie-breaks. The particular dynamics which emerge also depend upon the initial score-vector of the strategies and the initial history used to seed the start of the game. If the initial strategy score-vector is not 'typical', then a bias can be introduced into the game which never disappears. In short, the sys-tem never recovers from this bias. It will be assumed that no such initial bias exists. In practice this is achieved, for example, by setting all the initial scores to zero. The initial choice of history is not considered to be an important effect. It is assumed that any transient effects resulting from the particular history seed will have disappeared, i.e. the initial history seed does not introduce any long-term bias.
The strategy allocation among agents can be described in terms of a tensor Ω [34]. This tensor Ω describes the distribution of strategies among the N individual agents. If this strategy allocation is fixed from the beginning of the game, then it acts as a quenched disorder in the system. The rank of the tensor Ω is given by the number of strategies S that each agent holds. For example, for S =3 the element Ωi,j,k gives the number of agents as-signed strategy i, then strategy j, and then strategy k, in that order. Hence
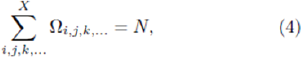

where the value of X represents the number of distinct strategies that exist within the strategy space chosen: X = 22m in the FSS, and X = 2.2m in the RSS. Figure 4 shows an example distribution H for N =101 agents in the case of m =2 and S =2, in the reduced strategy space RSS. We note that a single Ω 'macrostate’ corresponds to many possible 'microstates’ describing the speci c partitions of strategies among the agents. For ex-ample, consider an N = 2 agent system with S = 1: the microstate (R, R’) in which agent 1 has strategy R while agent 2has strategy R’, belongs to the same macrostate Ω as (R’, R) in which agent 1 has strategy R’ while agent 2 has strategy R. Hence the present Crowd-Anticrowd theory retained at the level of a given Ω, describes the set of all games which belong to that same macrostate. We also note that although Ω is not symmetric, it can be made so since the agents will typically not distinguish between the order in which the two strategies are picked. Given this, we will henceforth focus on S = 2 and consider the symmetrized version of the strategy allocation matrix given by Ψ = 1/2 ( Ω+ ΩT). In general, Ψ would be allowed to change in time, possibly evolving under some pre-de ned selection criteria. Changes in Ψ can in principle be invoked in order to control the future evolution of the multi-agent game: this corresponds to a change in heterogeneity in the agent population, and could represent the physical situation where individual agents (e.g.robots) could be re-wired, re-programmed, or replaced in order to invoke a change in the system's future evolution, or to avoid certain future scenarios or trajectories for the system as a whole.
In addition to the excess demand D[t] in such B-A-R systems, one is typically also interested in higher order-moments of this quantity for example, the standard deviation of D[t] (or 'volatility' in a financial context). This gives a measure of the fluctuations in the system, and hence can be used as a measure of 'risk' in the sys-tem. In particular the standard deviation gives an idea of the size of typical fluctuations in the system. However in the case that D[t] has a power-law distribution, the standard deviation may be a misleading representation of such risk because of the 'heavy tails' associated with the power- law [43]. Practical risk is arguably better associated with the probability of the system hitting a certain critical value (Dcrit), in a similar way to the methodology of financial Value-at-Risk [43]. However a note of caution is worthwhile: if there are high-order correlations in the system and hence in the time-series D[t] itself, any risk assessment based on Probability Distribution Functions over a fixed time-scale (e.g. single timestep) may be misleading. Instead, it may be the cumulative effects of a string of large negative values of D[t] which constitute the true risk, since these may take the system into dangerous territory. The possibility of designing a Collective in order to build in some form of immunization/resistance to such large cumulative changes or endogenous 'extreme events', or alternatively the possibility of performing 'on-line' soft control in an evolving system, is a fascinating topic. For simplicity, we will focus here on developing a description of D[t] and its standard deviation, noting that the same analytic approach would work equally well for other statistical functions of D[t].
Crowd-Anticrowd Formalism
Here we focus on developing a description of D[t] and its standard deviation. Similar analysis can be carried out for any function of D[t]. For example, the function f[D[t]]=[D[t] -<D[t]]α with α > 2, places more weighting on large deviations of D[t] from the mean. Alternatively, one may consider a function of past values {D[t’<t]}, such as the cumulative value P[t] =∑iD[ti < t], or any function of the constituent processes n+1[t] and n-1[t].
Consider an arbitrary timestep t during a run of the game, at which the particular realization of the strategy allocation matrix is given by Ψ. We will assume that is effectively constant over the time-window during which we will calculate the statistical properties of D[t]. There is a current score-vector S[t] and a current history μ[t] which de ne the state of the game. The excess demand D[t] = D [S[t], μ[t]] is given by Equation 1. The standard deviation of D[t] for this given run, corresponds to a time-average for a given realization of and a given set of initial conditions. It may turn out that we are only interested in ensemble-averaged quantities: consequently the standard deviation will then need to be averaged over many runs, and hence averaged over all realizations of and all sets of initial conditions.
Equation 1 can be rewritten by summing over the RSS as follows:
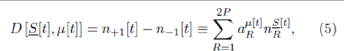
where P =2m. The quantity αμ[t]R=±1 is the response of strategy R to the history bit-string μat time t. The quantity 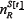 is the number of agents using strategy R at time t. The superscript
is the number of agents using strategy R at time t. The superscript 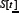 is a reminder that this number of agents will depend on the strategy score at time t. The calculation of the average demand D[t] will now be shown, where the average is over time for a given realization of the strategy allocation Ψ. We use the notation ⟨X[t]⟩t it to denote a time-average over the variable X[t] for a given Ψ. Hence
is a reminder that this number of agents will depend on the strategy score at time t. The calculation of the average demand D[t] will now be shown, where the average is over time for a given realization of the strategy allocation Ψ. We use the notation ⟨X[t]⟩t it to denote a time-average over the variable X[t] for a given Ψ. Hence
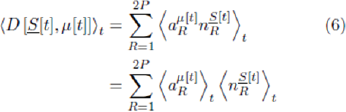
where we have used the property that 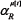 and
and 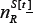 are uncorrelated. We now consider the special case in which all histories are visited equally on average: this may arise as the result of a periodic cycling through the history space (e.g. a Eulerian trail around the de Bruijn graph) or if the histories are visited randomly. Even if this situation does not hold for a specific Ψ, it may indeed hold once the averaging over Ψ has also been taken. For example, in the Minority Game all histories are visited equally at small m and a given Ψ: however the same is only true for large m if we take the additional average over all Ψ. Under the property of equal histories, we can write
are uncorrelated. We now consider the special case in which all histories are visited equally on average: this may arise as the result of a periodic cycling through the history space (e.g. a Eulerian trail around the de Bruijn graph) or if the histories are visited randomly. Even if this situation does not hold for a specific Ψ, it may indeed hold once the averaging over Ψ has also been taken. For example, in the Minority Game all histories are visited equally at small m and a given Ψ: however the same is only true for large m if we take the additional average over all Ψ. Under the property of equal histories, we can write
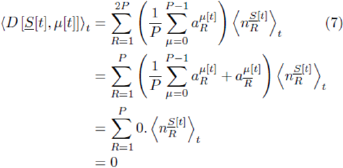
where we have used the exact result that αμ[t]R = 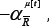 ,and the approximation
,and the approximation 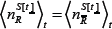 . strategy is approximately equal and hence
. strategy is approximately equal and hence 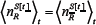 . In the event that all histories are not equally visited over time, even after averaging over all Ψ, it may still happen that the system's dynamics is restricted to equal visits to some subset of histories. An example of this would arise for m = 3, for example, for a repetitive sequence of outcomes ...00110011001 in which case the system repeatedly performs the 4-cycle...→ 001 → 011 → 110 → 100 → 001 +... In this case one can then carry out the averaging in Equation 7over this subspace of four histories, implying that there are now strategies that are effectively identical (i.e. they have the same response for these four histories, even though they differ in their response for one or more of the remaining four histories 000, 010, 101, 111 which are not visited). More generally, such sub-cycles within the de Bruijn graph may lead to a bias towards 1's or 0's in the global outcome sequence. We note that such a biased series of outcomes can also be generated by biasing the initial strategy pool.
. In the event that all histories are not equally visited over time, even after averaging over all Ψ, it may still happen that the system's dynamics is restricted to equal visits to some subset of histories. An example of this would arise for m = 3, for example, for a repetitive sequence of outcomes ...00110011001 in which case the system repeatedly performs the 4-cycle...→ 001 → 011 → 110 → 100 → 001 +... In this case one can then carry out the averaging in Equation 7over this subspace of four histories, implying that there are now strategies that are effectively identical (i.e. they have the same response for these four histories, even though they differ in their response for one or more of the remaining four histories 000, 010, 101, 111 which are not visited). More generally, such sub-cycles within the de Bruijn graph may lead to a bias towards 1's or 0's in the global outcome sequence. We note that such a biased series of outcomes can also be generated by biasing the initial strategy pool.
We will focus now on the fluctuations of D[t] about its average value. The variance of D[t], which is the square of the standard deviation, is given by
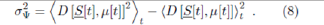
For simplicity, we will assume the game output is unbiased and hence we can set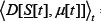 = 0 . As mentioned above,this might arise in a given system for a given Ψ, or after additional averaging over all possible configurations {Ψ}. We stress that this approximation does not have to be made -one can simply continue subtracting
= 0 . As mentioned above,this might arise in a given system for a given Ψ, or after additional averaging over all possible configurations {Ψ}. We stress that this approximation does not have to be made -one can simply continue subtracting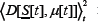 from the right hand side of the expression for σ2Ψ Hence
from the right hand side of the expression for σ2Ψ Hence
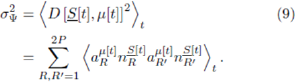
In the case that the system visits all possible histories equally, the double sum can usefully be broken down into three parts,based on the correlations between the strategies: 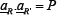 (fully correlated), (fully anti-correlated), and
(fully correlated), (fully anti-correlated), and 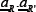 .cr,=-P (fully uncorrelated) where
.cr,=-P (fully uncorrelated) where 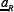 is a vector of dimension P with R'th component
is a vector of dimension P with R'th component 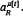 . This decomposition is exact in the RSS in which we are working. Again we note that if all histories are not equally visited, yet some subsets are, then this averaging can be carried out over the restricted subspace of histories. The equal-histories case yields
. This decomposition is exact in the RSS in which we are working. Again we note that if all histories are not equally visited, yet some subsets are, then this averaging can be carried out over the restricted subspace of histories. The equal-histories case yields
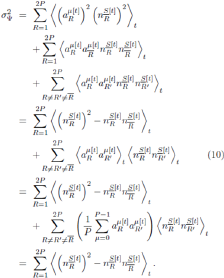
This sum over 2P terms can be written equivalently as a sum over P terms,
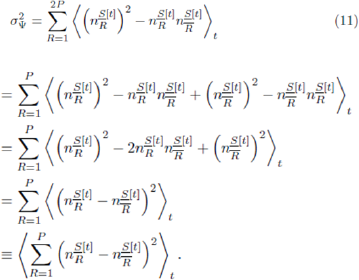
The values of 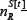 and
and 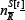 J for each R will depend on the precise form of Ψ. We now proceed to consider the ensembleaverage over all possible realizations of the strategy allocation matrix Ψ. The ensemble-average is denoted as ⟨...⟩Ψ, and for simplicity the notation
J for each R will depend on the precise form of Ψ. We now proceed to consider the ensembleaverage over all possible realizations of the strategy allocation matrix Ψ. The ensemble-average is denoted as ⟨...⟩Ψ, and for simplicity the notation 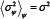 is defined. This ensembleaverage is performed on either side of Equation 11,
is defined. This ensembleaverage is performed on either side of Equation 11,
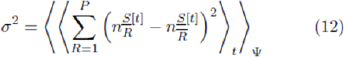
yielding the variance in the excess demand D[t]. Equation 12 is an important intermediary result for the Crowd-Anticrowd theory. It is straightforward to obtain analogous expressions for the variances in n+1[t] and n-1[t].
Equation 12 provides us with an expression for the time- averaged fluctuations. Some form of approximation must be introduced in order to reduce Equation 12 to explicit analytic expressions. It turns out that Equation 12 can be manipulated in a variety of ways, depending on the level of approximation that one is prepared to make. The precise form of any resulting analytic expression will depend on the details of the approximations made.
We now turn to the problem of evaluating Equation 12 analytically. A key first step is to relabel the strategies. Specifically, the sum in Equation 12 is re-written to be over a virtual-point ranking K and not the decimal form R. Consider the variation in points for a given strategy, as a function of time for a given realization of The ranking (i.e. label) of a given strategy in terms of virtual points score will typically change in time since the individual strategies have a variation in virtual-points which also varies in time. For the Minority Game, this variation is quite rapid in the low m regime since there are many more agents than available strategies -hence any strategy emerging as the instantaneously highest-scoring, will immediately get played by many agents and therefore be likely to lose on the next time-step. More general games involving competition within a multi-agent population will typically generate a similar ecology of strategy- scores with no all-time winner. [N.B. If this weren’t the case, then there would by definition be an absolute best, second-best etc. strategy. Hence any agent observing the game from the outside would be able to choose such a strategy and win consistently. Such a system is not sufficiently competitive, and is hence not the type of system we have in mind]. This implies that the specific identity of the ‘K’th highest-scoring strategy’ changes frequently in time. It also implies that varies considerably in time. Therefore in order to proceed, we shift the focus onto the time-evolution of the highest-scoring strategy, second highest- scoring strategy etc. This should have a much smoother timeevolution than the time-evolution for a given strategy. In short, the focus is shifted from the time-evolution of the virtual points of a given strategy (i.e. from SR[t]) to the time-evolution of the virtual points of the K’th highest scoring strategy (i.e. to SK[t]).
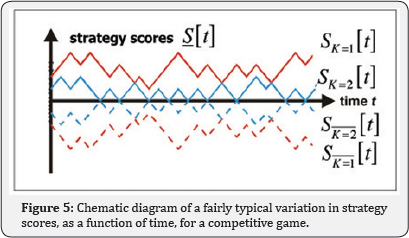
Figure 5 shows a schematic representation of how the scores of the two top scoring strategies might vary, using the new virtual-point ranking scheme. Also shown are the lowest- scoring two strategies, which at every timestep are obviously just the anticorrelated partners of the instantaneously highest- scoring two strategies. In the case of that the strategies all start off with zero points, these anticorrelated strategies appear as the mirror-image, i.e. SK [t] = . The label K is used to denote the rank in terms of strategy score, i.e. K = 1 is the highest scoring strategy position, K = 2 is the second highest-scoring strategy position etc. with
SK=1 > SK=2 > SK=3 > SK=4 > . . .(13)
assuming no strategy-ties. (Whenever strategy ties occur, this ranking gains a 'degeneracy' in that SK = SK+1 for a given K). A given strategy, e.g. -1- 1- 1- 1, may at a given timestep have label K = 1, while a few time step time steps later have label K = 5. Given that SR = - . (i.e. all strategy scores start o at zero), then we know that SK =- . Equation 12 can hence be rewritten exactly as
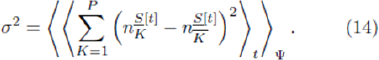
Now we make another important observation. Since in the systems of interest the agents are typically playing their highest- scoring strategies, then the relevant quantity in determining how many agents will instantaneously play a given strategy, is a knowledge of its relative ranking -not the actual value of its virtual points score. This suggests that the quantities 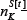 and
and 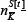 will fluctuate relatively little in time, and that we should now develop the problem in terms of time-averaged values.
will fluctuate relatively little in time, and that we should now develop the problem in terms of time-averaged values.
The actual number of agents 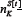 playing the K’th ranked strategy at timestep t, can be determined from knowledge of the strategy allocation matrix and the strategy scores S[t], in order to calculate how many agents hold the K'th ranked strategy but do not hold another strategy with higher-ranking. The heterogeneity in the population represented by Ψ, combined with the strategy scores S[t], determines
playing the K’th ranked strategy at timestep t, can be determined from knowledge of the strategy allocation matrix and the strategy scores S[t], in order to calculate how many agents hold the K'th ranked strategy but do not hold another strategy with higher-ranking. The heterogeneity in the population represented by Ψ, combined with the strategy scores S[t], determines 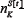 for each K and hence the standard deviation in D[t]. We can rewrite the number of agents playing the strategy in position K at any timestep t, in terms of some constant value nK plus a fluctuating term:
for each K and hence the standard deviation in D[t]. We can rewrite the number of agents playing the strategy in position K at any timestep t, in terms of some constant value nK plus a fluctuating term:
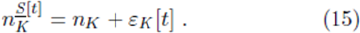
Consider a given timestep t in the game's evolution. Some strategies may be tied in virtual-points (i.e. they
are ‘degenerate’) while others are not (i.e. 'non-degenerate'). Depending on the rules of the game, such degeneracy may imply one of the following:
a) An agent must throw a coin to break a tie between any two de-generate strategies in his possession. In this case, any two agents holding the same pair of degenerate strategies may then disagree as to the ranking of the two strategies following the tie-break coin toss.
b) The Game-master must throw a master coin in order to produce a non-degenerate ranking. In this case, all agents will then agree on a unique virtual-point ranking of strategies.
c) An agent must preserve the ranking from the most recent timestep at which the two strategies weren’t degenerate.
Depending on the exact microscopic rule adopted, the global dynamics may differ. We will generally assume that rule:
a) Holds, since rule.
b) Might introduce large random fluctuations while rule.
c) Could favor deterministic cyclic behavior.
Suppose that an agent holds two strategies R and R’, and that they are non-degenerate at timestep t. suppose that they occupy ranks K and K + 1 respectively. Let the number of agents playing strategy R, the K'th ranked strategy, be nK at timestep t. Similarly the number of agents playing strategy R’, the (K + 1)'th ranked strategy, is nK+1 at timestep t. Hence εK[t] = 0 and εK+1[t] = 0 for this timestep, and indeed for all subsequent t until the next strategy-tie. Suppose that the two strategies R and R0 now become degenerate at timestep t+1. In a game where each agent resolves strategy tie-breaks using a coin-toss, then both R and R0 have probability 1=2 of being assigned the rank K at this timestep. This means that any agent holding strategies R and R’, will play R or R’ with probability 1=2. Hence such degeneracy acts to add disorder into the number of agents playing the K'th highest-scoring strategy. In particular, such coin-tosses at a given timestep t' will tend to reduce the number of agents playing higher- scoring strategies at that timestep (i.e. εK[t’] < 0 for small K) but will increase the number of agents playing lower-scoring strategies (i.e. εK[t’] > 0 for large K). Therefore if we were to completely ignore coin-tosses, we would tend to overestimate the number of people playing strategies which are higher- ranking (i.e. small K) and underestimate the number playing strategies which are lower-ranking (i.e. large K). This means that we will overestimate the size of Crowds, and underestimate the size of Anticrowds. Hence we will overestimate the value of the standard deviation of demand. [For this reason, the analytic expression adelta f that we will derive, slightly overestimates the actual value, and hence can be regarded as an approximate upper- bound.]. Accounting for the correct fraction of degenerate vs. non-degenerate timesteps, will yield a more accurate calculation of the time-average ⟨...⟩t in Equation 14. We will adopt this latter approach elsewhere for the network B-A-R system [47], thereby obtaining accurate analytic expressions which are in excellent quantitative agreement with numerical simulations.
Since our focus in this paper is more general, let us for the moment assume that we can choose a suitable constant nK such that the fluctuation εK[t] represents a small noise term. Hence,
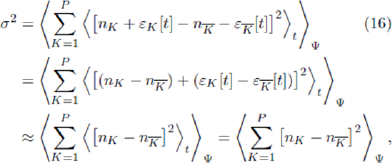
since the latter two terms involving noise will average out to be small. The resulting expression in Equation 16 involves no time dependence. The averaging over ¥ can then be taken inside the sum. The individual terms in the sum, i.e. 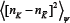 , are just an expectation value of a function of two variables nK and
, are just an expectation value of a function of two variables nK and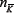 . Each term can therefore be rewritten exactly using the joint probability distribution for nK and , which we shall call P(nK,
. Each term can therefore be rewritten exactly using the joint probability distribution for nK and , which we shall call P(nK,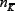 ). Hence
). Hence

where the standard probability result involving functions of two variables has been used.
In the event that Equation 17 is a reasonable approximation for the system under study, the question then arises as to how to evaluate it. In general, its value will depend on the detailed form
of the joint probability function P (nK , 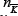 ) which in turn will depend on the ensemble of quenched disorders {Ψ} which are being averaged over. We start off by looking at Equation 17 in the limiting case where the averaging over the quenched disorder matrix is dominated by matrices Ψ which are nearly at. This will be a good approximation in the 'crowded’ limit of small m in which there are many more agents than available strategies, since the standard deviation of an element in (i.e. the standard deviation in bin-size) is then much smaller than the mean bin- size. [N.B. If is approximately at, then so is Ψ]. In this limiting case, there are several nice features:
) which in turn will depend on the ensemble of quenched disorders {Ψ} which are being averaged over. We start off by looking at Equation 17 in the limiting case where the averaging over the quenched disorder matrix is dominated by matrices Ψ which are nearly at. This will be a good approximation in the 'crowded’ limit of small m in which there are many more agents than available strategies, since the standard deviation of an element in (i.e. the standard deviation in bin-size) is then much smaller than the mean bin- size. [N.B. If is approximately at, then so is Ψ]. In this limiting case, there are several nice features:
Given the ranking in terms of virtual-points, i.e. SK=1 > SK=2 > Sk=3 > SK=4 > . . . which holds by de nition of the labels {K} if we neglect tie-breaks, we will also have
nK=1 > nK=2 > nK=3 > nK=4 > . . . (18)
Hence the rankings in terms of highest virtual-points and popularity are identical. By contrast, the ordering in terms of the labels {R} would not be sequential, i.e. it is not true that nR=1 > nR=2 > nR=3 > nR=4 >...
a) The strategy , which is anticorrelated to strategy K, occupies position = 2P +1-k in this popularity-ranked list.
b) The probability distribution P (nK, 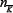 ) will be sharply
peaked around the nK and
) will be sharply
peaked around the nK and 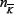 values given by the mean values for a at quenched-disorder matrix ¥ We will label these mean
values as
values given by the mean values for a at quenched-disorder matrix ¥ We will label these mean
values as 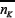 and
and 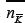 .
.
The last point implies that 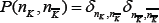 and so
and so
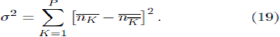
We note that there is a very simple interpretation of Equation 19. It represents the sum of the variances for each Crowd-Anticrowd pair. For a given strategy K there is an
anticorrelated strategy K. The 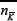 agents using strategy K are
doing the
agents using strategy K are
doing the 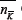 opposite of the agents strategy irrespective of the history bit-string. Hence the effective group-size for each Crowd-
Anticrowd pair is
opposite of the agents strategy irrespective of the history bit-string. Hence the effective group-size for each Crowd-
Anticrowd pair is 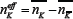 : this represents the net step-size d of the Crowd-Anticrowd pair in a random-walk contribu-tion to the total variance. Hence, the net contribution by this Crowd- Anticrowd pair to the variance is given by
: this represents the net step-size d of the Crowd-Anticrowd pair in a random-walk contribu-tion to the total variance. Hence, the net contribution by this Crowd- Anticrowd pair to the variance is given by
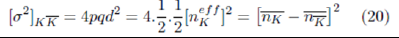
Where p =q=1/2 for a random walk. Since all the strong correlations have been removed (i.e. anticorrelations) it can therefore be assumed that the separate Crowd-Anticrowd pairs execute random walks which are uncorrelated with respect to each other. [Recall the properties of the RSS-all the remaining strategies are uncorrelated.]. Hence the total variance is given by the sum of the individual variances,
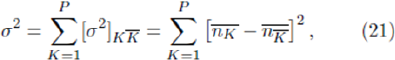
which corresponds exactly to Equation 19. If strategy- ties occur frequently, then one has to be more careful about evaluating 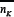 since its value may be affected by the tie- breaking rule. We will show elsewhere that this becomes quite important in the case of very small m in the presence of network connections - this is because very small m naturally leads to crowding in strategy space and hence mean-reverting virtual scores for strategies. This mean-reversion is amplified further by the presence of network connections which increases the crowding, thereby increasing the chance of strategy ties.
since its value may be affected by the tie- breaking rule. We will show elsewhere that this becomes quite important in the case of very small m in the presence of network connections - this is because very small m naturally leads to crowding in strategy space and hence mean-reverting virtual scores for strategies. This mean-reversion is amplified further by the presence of network connections which increases the crowding, thereby increasing the chance of strategy ties.
Implementation of Crowd-Anticrowd Theory
In this section we will consider the application of the Crowd- Anticrowd theory in some limiting cases. As suggested by the previous discussion, we will break the implementation of the Crowd-Anticrowd theory down into two separate regimes: small m, corresponding to many more agents than available strategies, and large m corresponding to the opposite case. Hence these two regimes are defined by the ratio of the number of strategies to agents being much less/greater than unity, and hence the strategy allocation matrix Ψ being densely/sparsely.
Flat quenched disorder matrix, small m
Each element of Ψ has a mean of N/(2P)S agents per ‘bin’. In the case of small m and hence densely-filled Ψ, the fluctuations in the number of agents per bin will be small compared to this mean value. For the case S = 2, the mean number of agents whose highest scoring strategy is the strategy occupying position K at timestep t, will therefore be given by summing the appropriate rows and columns of this quenched disorder matrix Ψ. Provides a schematic representation of Ψ with m=2, s=2, in the RSS. If the matrix Ψ is at, then any reordering due to changes in the strategy ranking has no effect on the form of the matrix. Therefore the number of agents playing the K’th highest-scoring strategy, will always be proportional to the number of shaded bins at that K (for K = 3). The shaded elements in Figure 5 therefore represent those agents who hold a strategy that is ranked third highest in score, i.e. K=3. In games where the agents use their highest scoring strategy, any agent using the strategy in position K=3 cannot have any strategy with a higher position. Hence the agents using the strategy in position K=3 must lie in one of the shaded bins. Since it is assumed that the coverage of the bins is uniform, the mean number of agents using the strategy in position K=3 is given by [48-50]:
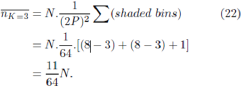
For more general m and s values this becomes
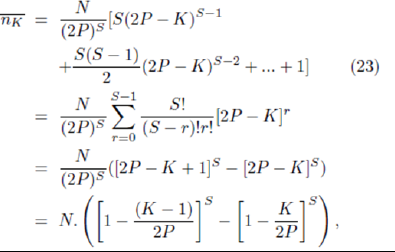
with P=2m. In the case where each agent holds two strategies, S = 2 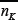 , can be simplified to
, can be simplified to
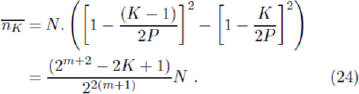
Similarly for 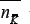 the simplification is as follows:
the simplification is as follows:
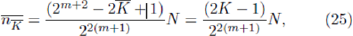
where the relation = 2P-K + 1=2m+1-K + 1 has been used. It is emphasized that these results depend on the assumption that the averages are dominated by the effects of at distributions of the quenched disorder matrix ¥, and hence will only be quantitatively valid for low m. Using Equations 24 and 25 in Equation 19 gives
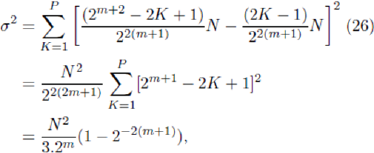
and hence
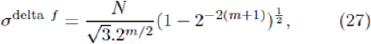
which is valid for small m. (The rationale behind the choice of superscript 'delta f will become apparent shortly.) This derivation has assumed that there are no strategy ties -more precisely, we have assumed that the game rules governing strategy ties do not upset the identical forms of the rankings in terms of highest virtual points and popularity. As discussed earlier, this tends to overestimate the size of the Crowds using high-ranking strategies, and underestimate the size of the Anticrowds using low-ranking strategies. Hence the Crowd- Anticrowd cancellation is underestimated, and consequently adelta f will overestimate the actual σ value.
Non-flat quenched disorder matrix Ψ, small m
The appearance of a significant number of non-flat quenched disorder matrices Ψ in the ensemble implies that the standard deviation for each ‘bin’ is now significant, i.e. non- negligible compared to the mean. This will be increasingly true as m increases. In this case, the general analysis is much more complicated, and should really appeal to the dynamics. However, an approximate theory can still be developed. The features for the case of ensembles containing a significant number of nonflat quenched disorder matrices Ψ become as follows:
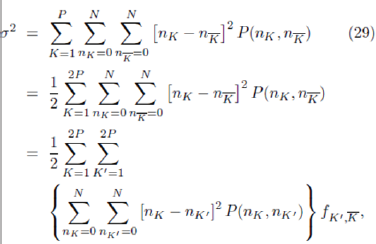
By definition of the labels {K}, the rank-ing in terms of virtual-points is retained, i.e. SK=1 >SK=2 >SK=3 >SK=4 > . . . is still always true in the absence of strategy ties. However the disorder in the matrix Ψ may distort the number of agents playing a given strategy to such an ex-tent, that it is no longer true that nK=1 > nK=2 > nK=3 > nK=4 > . . .Hence the rankings in terms of highest virtual-points and popularity are no longer identical. Another way of saying this is that the disorder in ¥ has introduced a disorder into the popularity ranking, such that it now differs from the virtual-point ranking. [We note that this disordering effect in the popularity ranking arising from the nonflat Ψ, occurs in addition to the disordering effect due to cointoss tie-breaking of strategy degeneracies discussed earlier].
In general we now have that nK' > nK” > nK”’> nK””> . . ., where the label K' need not equal 1, and K” need not equal 2 etc.. It is however possible to introduce a new label {Q} which will rank the strategies in terms of popularity, i.e.
nQ=1 > nQ=2 > nQ=3 > nQ=4 > . . . , (28)
where Q = 1 represents K’, Q = 2 represents K”, etc.
With this in mind, we will return to the original general form for the standard deviation of the excess demand in Equation 17, but rewrite it slightly as follows:
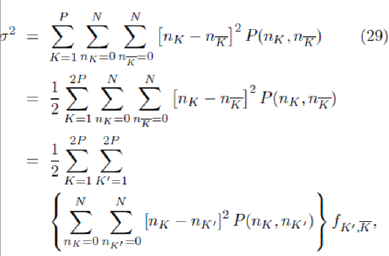
where fK0 ,K is the probability that K0 is the anticor-related
strategy to K (i.e. 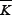 ) and is hence given by
) and is hence given by 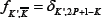 .
This manipulation is exact so far. A switch is now made to the popularity-labels {Q}.After relabelling, we obtain:
.
This manipulation is exact so far. A switch is now made to the popularity-labels {Q}.After relabelling, we obtain:
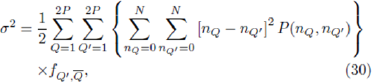
where  is the probability that the strategy with label Q' is anticorrelated to Q. Consider any particular strategy which was labelled previously by K and is now labelled by Q. Unlike the case of the at disorder ma-trix, it is not guaranteed that this strategy's anticorre-lated partner will lie in position Q'= 2P + 1-Q. All that can be said is that the strategy R has changed label from K→Q(K) while the anticorrelated strategy has changed label from
is the probability that the strategy with label Q' is anticorrelated to Q. Consider any particular strategy which was labelled previously by K and is now labelled by Q. Unlike the case of the at disorder ma-trix, it is not guaranteed that this strategy's anticorre-lated partner will lie in position Q'= 2P + 1-Q. All that can be said is that the strategy R has changed label from K→Q(K) while the anticorrelated strategy has changed label from 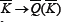 and that in general = 2P + 1-Q. As stated earlier, we have as a result of the relabelling that nQ=1 > nQ=2 > nQ=3 > nQ=4 > . ... It can be assumed that as a zeroth-order approximation the values of nQ=1, nQ=2, nQ=3,... etc. are still sharply peaked around their mean values obtained for the at- matrix case, i.e. it is assumed that the probability distribution P (nQ(K), nQ'(
and that in general = 2P + 1-Q. As stated earlier, we have as a result of the relabelling that nQ=1 > nQ=2 > nQ=3 > nQ=4 > . ... It can be assumed that as a zeroth-order approximation the values of nQ=1, nQ=2, nQ=3,... etc. are still sharply peaked around their mean values obtained for the at- matrix case, i.e. it is assumed that the probability distribution P (nQ(K), nQ'( 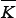 )) will be sharply peaked around the nQ(K) and nQ'(
)) will be sharply peaked around the nQ(K) and nQ'(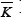 ) values given by the mean values for a flat matrix.As before, we will label these values
) values given by the mean values for a flat matrix.As before, we will label these values 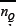 and
and 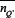 where the intrinsic dependence of Q on K has been dropped. Hence
where the intrinsic dependence of Q on K has been dropped. Hence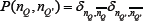 gives
gives
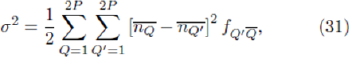
where the function 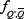 which is the probability that the strategy with label Q' is anticorrelated to strategy Q, still needs to be specified.
which is the probability that the strategy with label Q' is anticorrelated to strategy Q, still needs to be specified.
So what should the form of 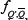 be? In the limit of negligible matrix disorder at small m, as studied in the previous section, it will be a delta-function at Q' = 2P + 1-Q= since in this case the rankings in terms of popularity and virtual-points will once more be identical. Hence we recover the results of the previous section. However, as the relative importance of disorder in ¥ increases, the delta-function form will no longer be appropriate. One approximate solution to this problem is to assume that the resulting disorder in the popularity ranking (as compared to the original virtual-point ranking) is so strong, that the probability that Q' is anticorrelated to Q becomes independent of the label Q' and is hence given by 1/(2P). Hence the anticorre-lated strategy to Q could lie anywhere in the strategy list { Q'} = 1, . . .2P. In this sense, this is the opposite limit to the delta-function case corresponding to the at disorder matrix at small m. Hence instead of being a delta-function at Q' = 2P + 1- Q, it now follows that
be? In the limit of negligible matrix disorder at small m, as studied in the previous section, it will be a delta-function at Q' = 2P + 1-Q= since in this case the rankings in terms of popularity and virtual-points will once more be identical. Hence we recover the results of the previous section. However, as the relative importance of disorder in ¥ increases, the delta-function form will no longer be appropriate. One approximate solution to this problem is to assume that the resulting disorder in the popularity ranking (as compared to the original virtual-point ranking) is so strong, that the probability that Q' is anticorrelated to Q becomes independent of the label Q' and is hence given by 1/(2P). Hence the anticorre-lated strategy to Q could lie anywhere in the strategy list { Q'} = 1, . . .2P. In this sense, this is the opposite limit to the delta-function case corresponding to the at disorder matrix at small m. Hence instead of being a delta-function at Q' = 2P + 1- Q, it now follows that 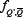 has a 'flat' form given by 1/(2P). In this limiting case we have
has a 'flat' form given by 1/(2P). In this limiting case we have
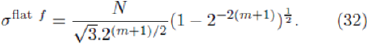
Comparing this with Equation 27 it can be seen that
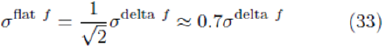
for the case of S = 2. The superscripts ‘flat f’ and ‘delta f’ used in the previous section, therefore can be seen to refer to the form
of the probability function 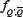 . We emphasize that Equation 27 can be derived from
. We emphasize that Equation 27 can be derived from 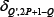 Equation 31 by letting take the delta-function form peaked at Q’= 2P + 1-Q≡
Equation 31 by letting take the delta-function form peaked at Q’= 2P + 1-Q≡ 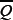 .
.
Non-flat quenched disorder matrix Ψ, large m
For larger m, the standard deviation in the number of agents in a given bin is now similar to the mean value. (By large m it is meant that the number of strategies is greater than N.s, i.e. 2.2m>N.s). Furthermore, there tend to be either 0 or 1 agents in each box (Q,Q’). In this limit, there will tend to be O(N) crowds, with each crowd having O(1) agent. Hence the popularity ordering is highly degenerate since nQ = 0,1 for all Q. Since the
anticorrelated strategy to Q could be anywhere, we have 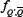 = 1/(2P ). Using Equation 31 then gives
= 1/(2P ). Using Equation 31 then gives
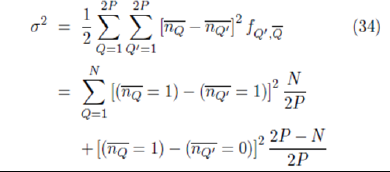
where the sum is now performed over the N strategies with one agent subscribed. Simplifying this expression gives
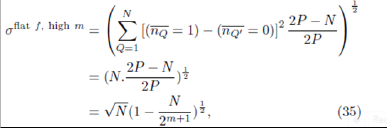
where P=2m has been used. We note in passing that it is quite simple to obtain a slightly more sophisticated approximation for which incorporates the agents’ behavior in picking their most successful strategy. For general S, this then yields
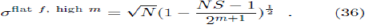
Reduced vs. full strategy space
The general dynamics for a typical game are likely to be similar in character when played in both the FSS and the RSS [14]. Hence the RSS-based Crowd-Anticrowd theory would generally be expected to provide a valid description for games played in the FSS as well. In addition to straightforward numerical demonstration for the particular game of interest, there is a theoretical justification which goes as follows. For a game played in the FSS.
There are 22m/2.2m distinct subsets of strategies. Each subset can be considered as a separate RSS. Note that the strategies that belong to a given RSS are optimally spread out across the corresponding FSS hypercube. Figure 2 shows the distribution of the 16, m=2 strategies across the 4 dimensional hypercube. The positions of the strategies belonging to the RSS are such that no two strategies have a Hamming separation less than 2m/2. The same can be said for any other choice of RSS. Due to the nature of a RSS, and given similar strings of past outcomes over which to score strategies, each strategy within the RSS attains a score in an uncorrelated or anticorrelated manner to any other strategy in the subset. Any other RSS within the FSS will score its strategies in a similar way, although slightly out of phase. For ex-ample for m=3, the rst RSS to be considered could contain the strategy 00001111, and the second RSS con-sidered could contain the strategy 01001111. It is easy to see that on 7 out of 8 occasions these two strategies would score in the same way. Hence it can be seen that these two strategies from two separate RSS, will follow each other during a typical run of an unbiased game. This argument extends across all strategies in all of the 22m/2.2m distinct RSS’s within the FSS. Hence a game using the FSS behaves as if there are 2.2m clusters of strategies and so is similar to a game played in the RSS. These clusters form the Crowds and Anticrowds of the theory, and this clustering allows the use of just one RSS in the theory.
Figure 5 Schematic diagram of a fairly typical variation in strategy scores, as a function of time, for a competitive game. This behavior is particularly relevant for the low m regime where there are many more agents than strategies, and hence strategy rankings change in time due to being overplayed. The strategies at any given time step can be ranked in terms of virtual-point ranking K, with K=1 as the highest-scoring and  1 as the lowest-scoring. The actual identity of the strategy in rank K changes a time progresses, as can be seen. Ignoring accidental ties in score, there is a well de ned ranking of strategies at each time step in terms of their K values [43].
1 as the lowest-scoring. The actual identity of the strategy in rank K changes a time progresses, as can be seen. Ignoring accidental ties in score, there is a well de ned ranking of strategies at each time step in terms of their K values [43].
Conclusion
We have outlined a Crowd-Anticrowd theory in order to understand the uctuations in collections of biomedical systems. Since the theory incorporates details concerning the structure of the strategy space, and its possible coupling to history space, we believe that the Crowd-Anticrowd theory will have applicability for more general multi-agent systems. Hence we believe that the Crowd-Anticrowd concept might serve as a fundamental theoretical concept for more general Complex Systems which mimic competitive multi-agent games. This would be a welcome development, given the lack of general theoretical concepts in the field of Complex Systems as a whole. It is also pleasing from the point of view of physics methodology, since the basic underlying philosophy of accounting correctly for 'interparticle’ correlations is al-ready known to be successful in more conventional areas of many-body physics. This success in turn raises the intriguing possibility that conventional many- body physics might be open to re-interpretation in terms of an appropriate multi-particle 'game': we leave this for future work.
Some properties of multi-agent games cannot be de-scribed using time-and configuration-averaged theories. In particular, an observation of a real-world Complex System which is thought to resemble a multi-agent game, may correspond to a single run which evolves from a specific initial configuration of agents' strategies. This implies a particular ¥, and hence the time- averagings within the Crowd-Anticrowd theory must be carried out for that particular choice of Ψ. However this problem can still be cast in terms of the Crowd-Anticrowd approach, since the averagings are then just carried out over some sub-set of paths in history space, which is conditional on the path along which the Complex System is already heading. We also emphasize that a single 'macrostate’ corresponds to many possible 'microstates’, where each microstate corresponds to one particular partition of strategy allocation among the agents. Hence the Crowd- Anticrowd theory retained at the level of a given specified ¥, is equally valid for the entire set of games which share this same 'macrostate’.
We have been discussing a Complex System based on multi-agent dynamics, in which both deterministic and stochastic processes co-exist, and are indeed inter-twined. Depending on the particular rules of the game, the stochastic element may be associated with any of five areas:
a) Disorder associated with the strategy al-location and hence with the heterogeneity in the population,
b) Disorder in the underlying network. Both (i) and (ii) might typically be fixed from the outset (i.e., quenched disorder) hence it is interesting to see the interplay of (i) and (ii) in terms of the overall performance of the system. The extent to which these two 'hard-wired' disorders might then compensate each other, as for example in the Parrondo effect or stochastic resonance, is an interesting question. Such a compensation effect might be engineered, for example, by altering the rules-of-the-game concerning inter-agent communication on the existing network. Three further possible sources of stochasticity are
c) Tie-breaks in the scores of strategies,
d) A stochastic rule in order for each agent to pick which strategy to use from the available S strategies, as in the Thermal Minority Game,
e) Stochasticity in the global resource level L[t] due to changing external conditions. To a greater or lesser extent, these five stochastic elements will tend to break up any deterministic cycles arising in the game. In the case of (iii), the stochasticity due to tie-breaks, we note that this stochasticity may actually have a physical significance. Suppose a real agent is at a deadlock in terms of which strategy to use at a particular timestep: some additional microscopic factor may then become important in determining the particular strategy that the agent follows (e.g. power level in the case of mechanical agents) hence breaking the tie. In this way, the coin-toss mimics the effect of this additional microscopic characteristic of the individual agents, which had been left out of the original game.
The future therefore looks very interesting for these Bi-nary Agent Resource models. By moving beyond the con-fines of the El Farol Problem and Minority Games for example by introducing underlying network structures and generalized game rules the possibility exists for pursuing a general yet cohesive path through the Complex Systems landscape.
Acknowledgement
We are grateful to Pak Ming Hui, Michael Hart and Paul Je eries for their earlier input to this work, to-gether with Sehyo Charley Choe, Sean Gourley and David Smith.
References
- Odeyemi K, Ogunti E (2014) Performance comparison of multiple input multiple output techniques for high data rate wireless communication system. Journal of Computational Intelligence and Electronic Systems 3(1): 36-43.
- Groumpos PP (2014) Intelligent decision making support systems: issues and challenges. Journal of Computational Intelligence and Electronic Systems 3(2): 122-131.
- Kumar K, Goyal P (2014) A Review on energy minimization techniques in wireless sensor network. Journal of Computational Intelligence and Electronic Systems 3(1): 1-10.
- Casti JL (1997) Would-be Worlds (Wiley, New York, USA).
- Casti JL (1995) Complexi cation (Abacus, London,).
- Sole RV, Goodwin B (2000) Signs of Life: how complexity pervades biology (Basic Books, New York, USA).
- Bossomaier T, Green D (1998) Patterns in the Sand: Computers, Complexity and Life (Allen Unwin, Sydney, USA), 74(4): 458.
- Holland JH (1998) Emergence (Oxford University Press, UK).
- Gell Mann M (1998) The Quark and the Jaguar (Abacus).
- See the works of D Wolpert, K Tumer. Elsewhere in this volume.
- Arthur B (1999) Amer Econ Rev 84: 406 (1994); Science 284, 107 (1999).
- Johnson NF, Jarvis S, Jonson R, Cheung P, Kwong Y, et al. (1998) Physica A 258: 230.
- Challet D, Zhang YC (1997) Physica A 246: 407.
- Challet D, Zhang YC (1998) Physica A 256: 514.
- Marsili M, Challet D (2001) Phys Rev E 64: 056138.
- Challet D, Marsili M (1999) Phys Rev E 60: 6271.
- Challet D, Marsili M, Zecchina R (1999) Phys Rev Lett 82: 2203.
- Challet D, Marsili M, Zhang YC (2001) Physica A 294: 514.
- Marsili M, Challet D (2000) Adv Complex Systems 1: 1.
- Marsili M, Challet D, Zecchina R (2000) Physica A 280: 522.
- Challet D, Marsili M (2000) Phys Rev E 62: 1862.
- Challet D, Marsili M, Zecchina R (2000) Phys Rev Lett 85: 5008.
- Savit R, Manuca R, Riolo R (1999) Phys Rev Lett 82: 2203. Interestingly, we had found a similarly shaped curve for the volatility in the El Farol problem (see Ref. [12]).
- Li Y, Riolo R, Savit R (2000) Physica A 276: 234.
- Li Y, Riolo R, Savit R (2000) Physica A 276: 265.
- Johnson NF, Hart M, Hui PM (1999) Physica A 269: 1.
- Hart M, Jeeries P, Johnson NF, Hui PM (2001) Phys-ica A 298: 537.
- Johnson NF, Hui PM, Dafang Zheng, Hart M (1999) J Phys A: Math Gen 32: L427.
- Hart ML, Jeeries P, Johnson NF, Hui PM (2001) Phys Rev E 63: 017102.
- Jeeries P, Hart M, Johnson NF, Hui PM (2000) J Phys A: Math Gen 33: L409.
- We presented the Grand Canonical Minority Game (GCMG) model at the APFA1 conference in Dublin (1999) and at the rst International Workshop of Ap-plications of Statistical Physics to Financial Analysis in Palermo (September 1998). See also Ref. [35].
- Hart ML, Je eries P, Johnson NF (2002) Physica A 311: 275.
- Hart ML, Lamper D, Johnson NF (2002) Physica A 316: 649.
- Je eries P, Hart ML, Johnson NF (2002) Phys. Rev. E 65, 016105 (2002).
- Johnson NF, Hart M, Hui PM, Zheng D (2000) Int J of Th and Applied Fin 3: 443.
- Johnson NF, Hui PM, Jonson R, Lo TS (1999) Phys Rev Lett 82: 3360.
- Heimel JAF, Coolen ACC (2001) Phys Rev E 63: 056121.
- Heimel JAF, Coolen ACC, Sherrington D (2001) Phys Rev E 65: 016126.
- Cavagna A (1999) Phys Rev E 59: 3783.
- Cavagna A, Garrahan JP, Giardina I, Sherring ton D (2000) Phys Rev Lett 83: 4429; A Cavagna, JP Garrahan, I Giardina, D Sherrington (2000) Phys Rev Lett 85, 5009.
- Garrahan JP, Moro E, Sherrington D (2001) Quant. Fi-nance 1: 246.
- http://www.unifr.ch/econophysics/minority
- Johnson NF, Je eries P, Hui PM (2003) Financial Market Complexity (Oxford University Press), UK.
- Newman MEJ, Barabasi AL, Watts DJ (2003) (2001 The Structure and Dynamics of Networks, (Princeton University Press) USA, SH Strogatz, Nature 410: 268.
- Dorogovtsev SN, Mendes JFF (2003) Evolution of Net-works: From Biological Nets to the Internet and WWW, (Oxford University Press).
- Tlalka M, Hensman D, Darrah PR, Watkinson SC, Fricker MD (2003) New Phytologist 158: 325.
- Challet D, Johnson NF (2002) Phys Rev Lett 89: 028701.
- Choe C, Gourley S, Hui PM, Johnson NF (in preparation).
- The Thermal Minority Game discussed in Ref. [40] de-pends on a parameter T (or equivalently 1=) called a 'temperature'. We could similarly de ne T by set-ting the probability of playing the worst strategy = e =(e + e ). Hence T = 2[ln( 1 1)] 1. T = 0 cor-responds to = 0 while T ! 1 corresponds to ! 1=2, hence we will only consider 01=2.
- Anghel M, Toroczkai Z, Bassler KE, Korniss G (2004) Phys Rev Lett 92: 058 701.






























