A Parametric Study of the Free Undamped Torsional Vibration of One-Dimensional Structural Elements using the Differential Quadrature Method (DQM)
Mohamed ElShabrawy1,2, Engy Abd ElHadi Amin1*, Salah Eldin Besheer1 and Mostafa A. M. Abdeen1
1Department of Engineering Mathematics and Physics, Cairo University, Egypt
2Smart Engineering Systems Research Center (SESC), Nile University, Egypt
Submission: February 16, 2022; Published: May 17, 2022
*Corresponding Author: Engy Abd ElHadi Amin, Department of Engineering Mathematics and Physics, Cairo University, Giza, Egypt
How to cite this article:Mohamed ElShabrawy, Engy Abd ElHadi Amin, Salah Eldin Besheer, Mostafa A. M. Abdeen1. A Parametric Study of the Free Undamped Torsional Vibration of One-Dimensional Structural Elements Using the Differential Quadrature Method (DQM).Civil Eng Res J. 2022; 13(1): 555853. DOI 10.19080/CERJ.2022.13.555853
Abstract
Recently, structures prone to torsional vibration have grabbed the interest of the structural engineering field whose aim has become to design structures with increased torsional stiffness. To the author’s limited knowledge, studies researching this topic couldn’t provide a simplified method to obtain the natural torsional frequencies and the corresponding mode shapes of structures providing ease of use by structural engineers having limited mathematical backgrounds. The purpose of this study is to establish a simplified numerical model of the torsional vibration of rods with non-uniform geometry and material with classical boundary conditions using the differential quadrature method (DQM). To account for geometric and material non- uniformity, any space varying functions in the longitudinal direction of a one- dimensional structural element can be used in the model. The numerical results obtained are compared with previously obtained analytical results in cases of rods with uniform cross sections and linearly non-uniform ones. The comparison proved significant agreement with the analytical results. The illustrated use of the DQM showed efficiency and acceptable accuracy that made it legible to create an alternative to the time-consuming analytical solutions that require a unique solution technique for every type of structural variation where a strong mathematical background of the user is needed.
Keywords: Torsional vibration; Non-uniform rods; Mode shapes; Natural frequencies; Differential quadrature method
List of Symbols
J: Mass Polar Moment of Inertia (mass. length2) I: Area Polar Moment of Inertia (length4)
G: Material Shear Modulus (force. length-2) Mt: Internal torsional moment (force. length)
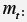 External applied torsional moment (force. length)
External applied torsional moment (force. length)
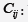 Weighting Coefficients of the Differential Quadrature Method
Weighting Coefficients of the Differential Quadrature Method
Greek Letters
ρ: Material density. (mass/length)
Θ: Cross-sectional twist angle. (rad)
ω: Natural circular frequency (rad/sec)
Introduction
Torsional vibration of structural elements has become a point of interest to the structural engineering field especially after the dreadful failure of the Tacoma Narrows bridge (or the Galloping Gertie) in 1940. Ever since Tacoma’s collapse, structures prone to torsional vibration have grabbed the interest of the structural engineering field whose aim has become to analyze and design structures with increased torsional stiffness to overcome flutter and torsion-based failures [1-3]. In 2014 Andersen et al. [1] proposed a method for non-flutter design by setting the torsional-to-vertical frequency ratio below 1 which made it a must to find a quick way to calculate the dominant torsional frequencies of structures. Obtaining the torsional vibration frequencies and corresponding mode shapes for structural elements having constant sections is an old problem that had been solved long ago as referred to in the literature hereunder, but what if the addressed structural element is subjected to a variation along its length whether it was cross sectional or a material variation or both at the same time? Structural elements natural frequencies and vibration modes are commonly computed by one of the following methods: (i) analytical; (ii) approximation techniques or semi-analytical and (iii) numerical methods [4]. One should bear in mind that it is an accuracy vs time choice. Many researchers used analytical techniques to study the torsional frequencies and vibration modes of rods with classical boundary conditions and variable cross sections. In torsional vibration problems the cross-sectional variation is translated into polar moment of inertia variation along the studied element’s length, while the material variation is translated into a variable shear modulus along the element’s length. These analytical techniques set a requirement to fully define the moment of inertia and shear modulus variation equations that are to be used in the differential equations before digging deep into the solution to be compatible with the mathematical techniques at hand [5-8]. Li QS [6] didn’t only present a solution for rods with variable cross sections with specific equations, he also added to the solution recurrence formulae to obtain the torsional vibration frequencies and vibration modes of a multi-step nonuniform rod carrying an arbitrary number of concentrated elements with classical or nonclassical boundary conditions which made the solution semi-analytical and still couldn’t account for any material changes occurring along the rod’s length.
Bridges were not the only structures that grabbed the researchers’ attention from the point of-view of torsional vibration. With the introduction of high-rise buildings to the modern urban world, accounting for torsional vibrational effects became an inseparable part of the design process. Most of these buildings exhibit non-uniformity whether on each structural element scale or the building as a whole which require largescale prototypes and simulations based on simplified numerical models to ensure better efficiency. In 1982 Basu & Dar [9] were from the first who discretized multi-storey buildings to be modelled as coupled beams. Then in 1996 a new model was proposed by Miranda [10] that solves a multi-storey building as a deformable continuous cantilever beam which was developed again by Miranda & Taghavi [11] to consider the stiffness nonuniformity in the different modelled storeys. In 2001, the same authors created simpler formulae [12] under the “Equivalent Column” concept which could evaluate the natural frequencies of multi-storey buildings in the 3 directions. Starting from 2009 till 2014, approximate solutions were proposed [13-14] to tall buildings taking into consideration the interaction between the vertical and torsional modes. Starting from 2014, Piccardo et al. [15] introduced the equivalent beam model which could simulate the dynamic behaviour of three-dimensional structures modelled as beams and this model has been adopted ever since for studying the aeroelastic instability and nonlinear behaviour of structures [16-18]. In 2020, [19] a beam-like model was proposed that was suitable for buildings with irregularities and unsymmetrical plans that was mainly created to check the seismic performance of already existing structures. This model presented the dominant mode shapes that frequently occurred to specific reinforced concrete structures. Its results were specifically concerned with the 1st two transitional mode shapes and only the 3rd torsional mode shape along with reproducing the time history of a chosen point on the structure. As stated, the research history is full of models and methods that could solve regular structural vibration problems but, to the author’s limited knowledge, none could propose a simple solution method focused on the torsional vibration of non-uniform structures. Noteworthy is that the methods listed in the literature, for sure, have their immanent advantages as well as drawbacks when it comes to the accuracyefficiency relationship. Choosing the conventional analytical methods results in the best possible accuracy but takes up a lot of time and effort unlike the semi-analytical and numerical methods that offer acceptably less accuracy, but significantly less computational time and flexibility given that the rationale upon which the numerical technique is based is correct in the first place. One of the numerical techniques usually used in civil engineering problems is the Differential Quadrature Method or the (DQM). The Differential Quadrature Method (or the DQM) was first proposed by Bellman & Casti [20] as a new technique to solve ordinary and partial differential equations and could bridge the gap between complex mathematics and civil engineering. [20, 21] Returning to the question posed earlier regarding the material variation and cross- sectional variation occurring at the same time, to the best of the author’s limited knowledge, no such closed-form solution has been reported yet which makes the work presented hereunder a tiny new brick in the edifice of knowledge.
Formulation
Mathematical Derivation and Governing Equations
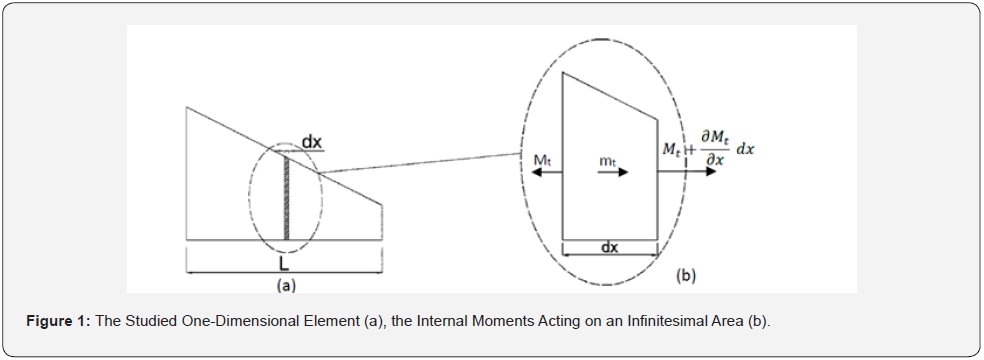
A one-dimensional structural element of length L, mass polar moment of inertia I ( x), area polar moment of inertia J (x) , shear modulus G( x), and density ρ ( x) is modelled as shown in (Figure 1) [22, 23]. Summing the torsional moments about z-axis and apply in Newton’s 2nd law for rotation:
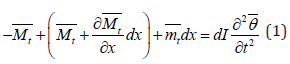
Knowing that 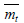 is the external applied torsional moment, dI
is the mass moment of inertia about the z-axis of the infinitesimal
element, and θ is the rotation angle (in radians) of the crosssection;
θ =θ ( z,t ) therefore:
is the external applied torsional moment, dI
is the mass moment of inertia about the z-axis of the infinitesimal
element, and θ is the rotation angle (in radians) of the crosssection;
θ =θ ( z,t ) therefore:
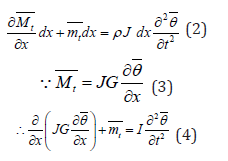
Considering as harmonic functions:
as harmonic functions:
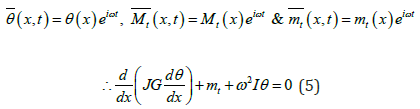
Since we are solving a free vibration problem, 𝑚𝑡 is eliminated from equation (5) as follows:
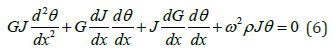
Since a generic analytical solution of equation (6) is hard to reach to account for any cross-sectional or material variation along the one-dimensional element’s length, the DQM is implemented to solve it numerically. The DQM is a handy method that is widely used in structural engineering problems consisting of higher orders differential equations as stated by Rajasekaran S [24]. The DQM implementation to obtain the torsional natural modes of the one-dimensional element described by equation (6) is presented hereunder.
DQM and Solution Procedure
The Differential Quadrature Method was first proposed by Bellman & Casti [20] as a new technique to solve ordinary and partial differential equations and by applying Wilson’s boundary conditions [21] the DQM has been widely used by engineers as it offered a straightforward method that can be easily deployed to detangle the complexity of differential equations. The DQM is appealing for the use in engineering problems due to its simplicity in transforming a complex differential equation into more engineering-friendly equations that need little computational time and effort to be solved. The ethos of the DQM is to get the derivative of a function in the form of the summation of estimated weighted coefficients multiplied by the original function itself at specified locations within the solution domain without digging deep in each derivative equation on its own as shown hereunder [24].
For a function f ( x) , the DQ approximation of the kth derivative at the ith grid point is calculated by:
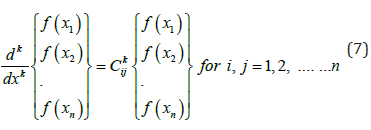
Where n is the number of grid points [21], [24-25].
Numerical Discretization
Since the DQM is, after all, a numerical method, the solution accuracy will eventually be affected by the quantity and quality (the distribution) of the sampling points. Chebyshev–Gauss– Lobatto mesh distribution is usually deployed to structural vibration problems to guarantee full coverage of the structural element with extra focus on the edges to better apply the boundary conditions as shown in (Figure 2) [25].
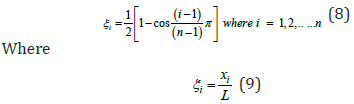
And L is the one-dimensional element’s length but for the ease
of visualization, non-dimensionalization of the whole equation
is made which makes 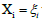 where xi is the distance from the left
edge of the element if it is a horizontal structural element and
is the distance from the bottom if it is a vertical one. Note that if
the column is divided into
where xi is the distance from the left
edge of the element if it is a horizontal structural element and
is the distance from the bottom if it is a vertical one. Note that if
the column is divided into 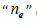 divisions then the sampling points
divisions then the sampling points
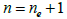 .
.

The weighting coefficients are calculated at each grid point using the following procedure:
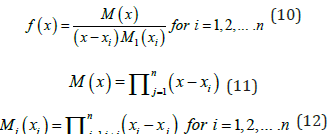
The weighting coefficient matrices’ elements are calculated as follows:
1. The elements of the weighting coefficients’ matrix 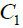 of
the 1st derivative are calculated as follows:
of
the 1st derivative are calculated as follows:
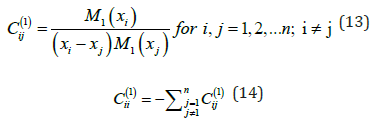
2. The elements of the weighting coefficients’ matrix 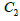 of
the 2nd derivative are calculated as follows:
of
the 2nd derivative are calculated as follows:
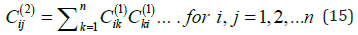
Applying the weighting coefficients’ matrices to equation (6) gives the following final form:
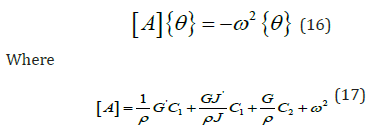
Note that the derivatives of G( x)and J (x) could too be calculated with the same technique (the DQM) in cases of severely complex functions. With proper implementation of the boundary conditions as per Wilson et al. [21], the equation becomes ready to be solved as an eigen value problem to obtain the torsional natural frequencies of the addressed element along with the corresponding torsional mode shapes. The effects of several parameters were studied in this work which are: crosssectional variation (linear and parabolic) along the element’s length (Variable J (x) ), material variation (linear and parabolic) along the element’s length (variable G( x)&ρ ( x) ) and the effect of changing both parameters (linear and parabolic) at the same time while using classical boundary conditions (fixed-fixed, free-free, or fixed- free).
Results, Validation and Discussion
Results and Validation
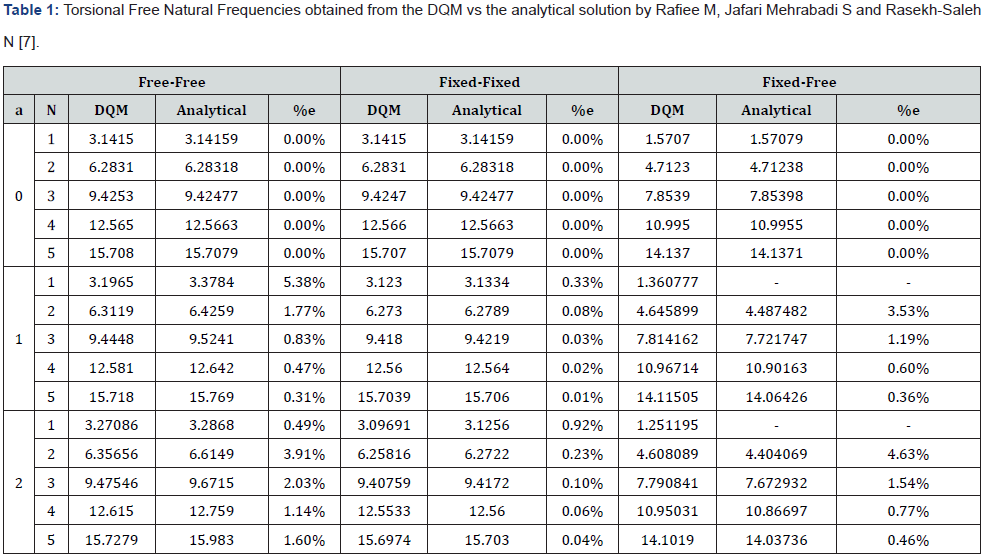
In this section, the computational numerical results of the proposed DQM are presented and compared with the results obtained analytically by Rafiee M, Jafari Mehrabadi S and Rasekh- Saleh N [7]. Then after validation, the effects of several parameters such as end conditions, moment of inertia and material are presented. Rafiee M, Jafari Mehrabadi S and Rasekh-Saleh N [7] derived an analytical solution to equation (6) with a constant shear modulus(G) and with varying inertia according to equation (18).
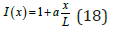
For a constant cross-section: “ a ” is substituted by 0 and for a linearly varying cross-section: “ a ” is substituted once by 1 and once by 2. The same parameters were used, and equation (6) was solved using the DQM. (Table 1) presents the comparison between the numerical results obtained by the DQM and the results obtained analytically by Rafiee M, Jafari Mehrabadi S and Rasekh- Saleh N [7] showing a maximum error of 5.4% in the first linear variation ( a =1) with fixed-free end condition.
Discussion
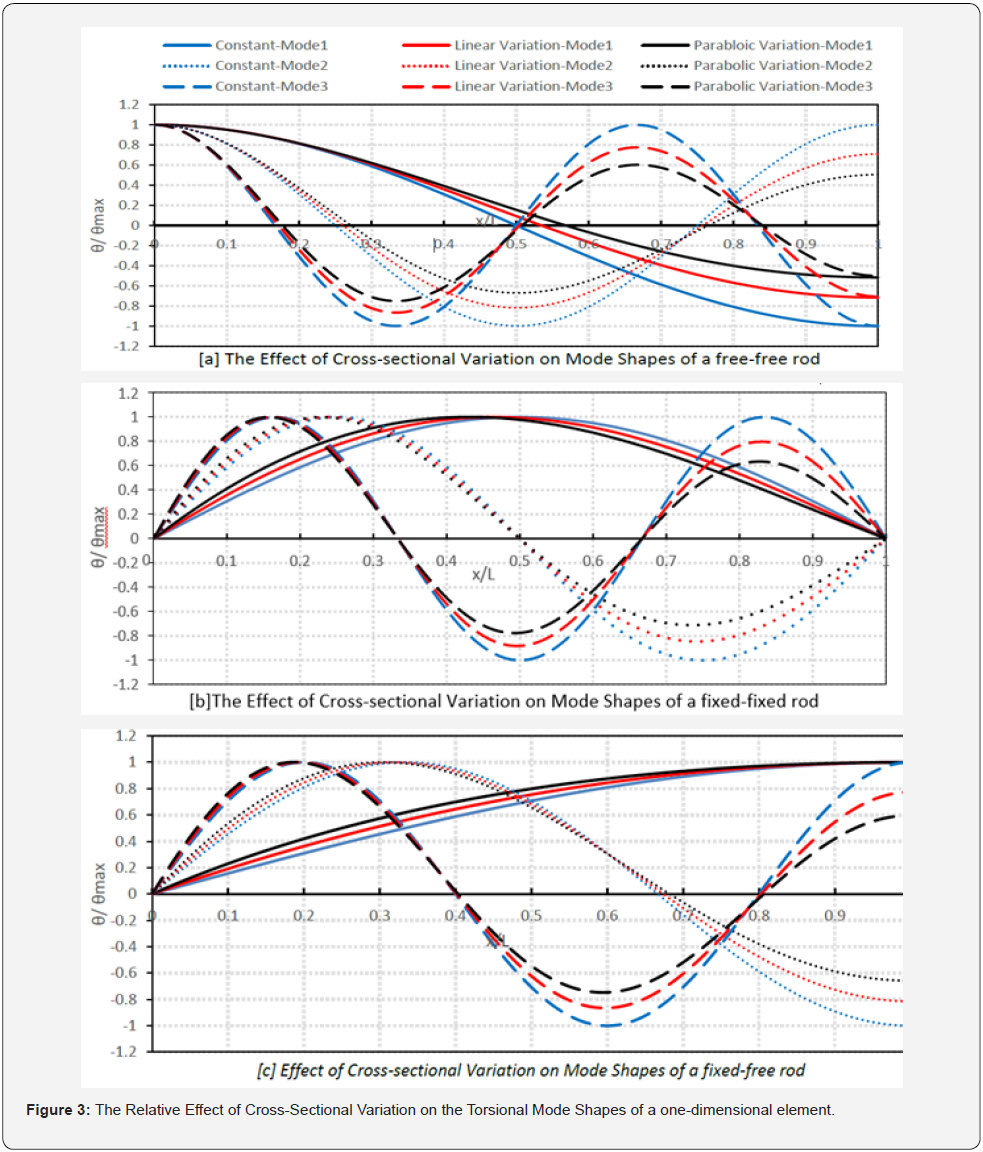
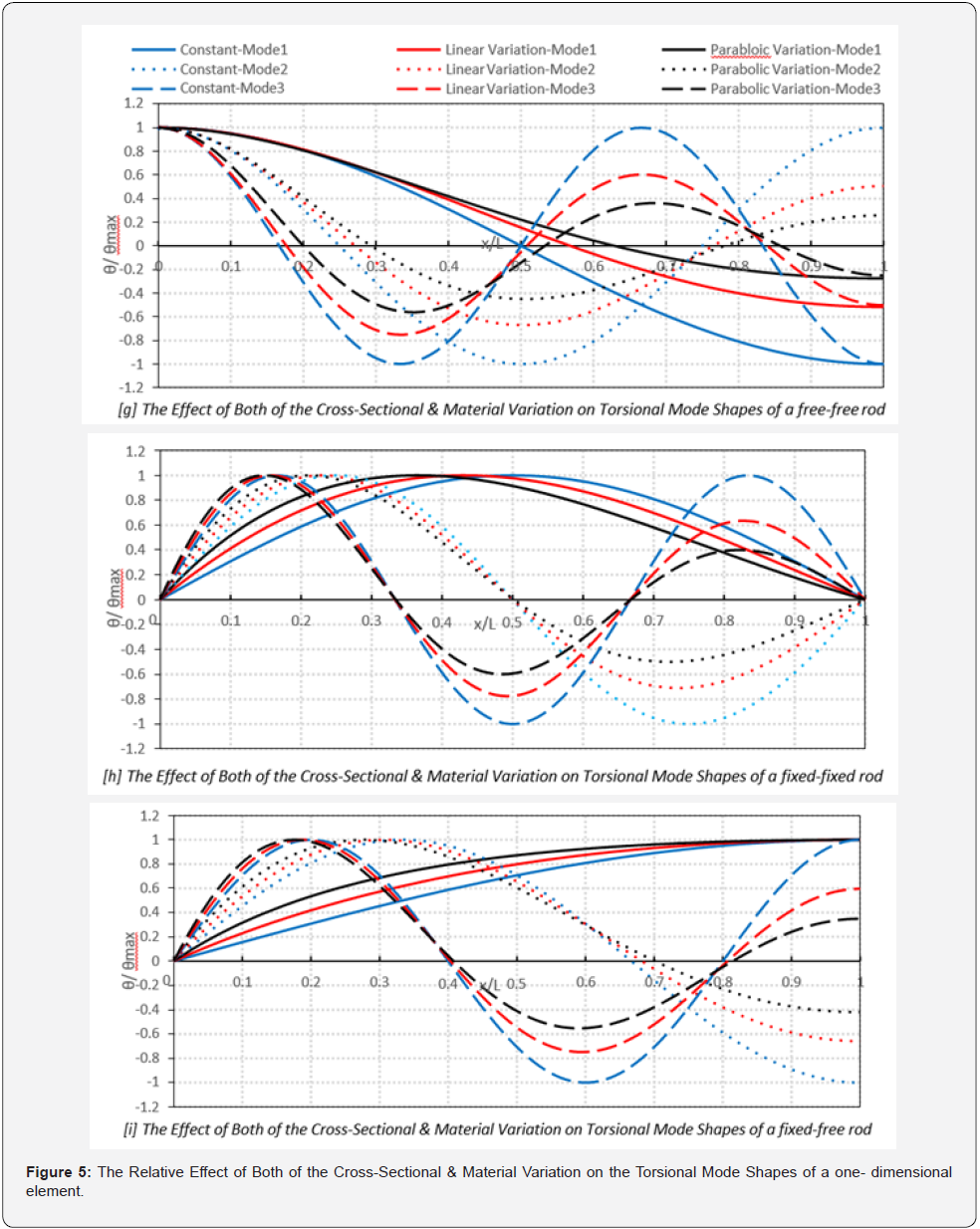
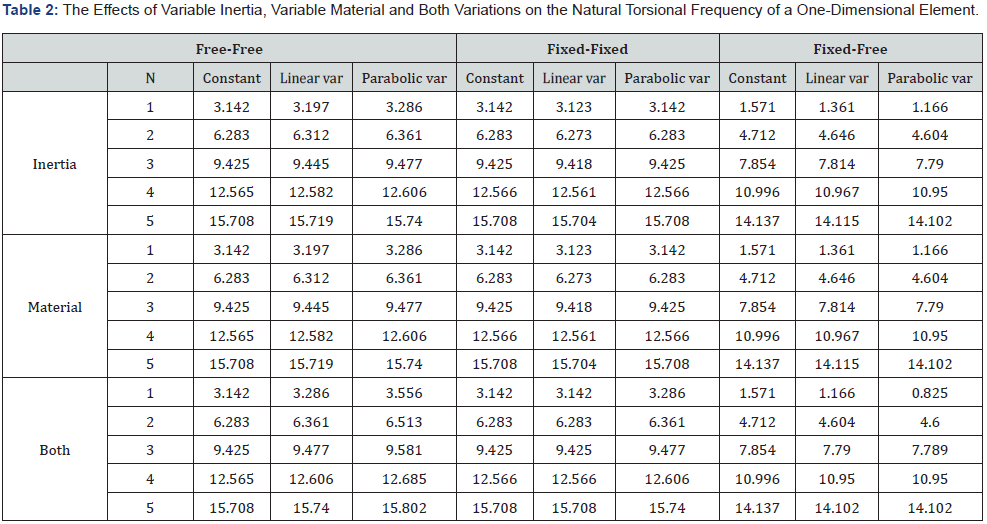
Changing the one-dimensional element’s cross-sectional inertia or material along its length or changing both and applying those to the three basic boundary conditions (free-free, fixed-fixed, and fixed-free) affects the element’s natural torsional frequencies (refer to (Table 1) and (Table 2)) along with its torsional mode shapes refer to (Figure 3, Figure 4, & Figure 5) respectively.

Note that: linear variation means: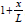 and parabolic variation means:
and parabolic variation means: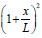
Note that: linear variation means: 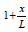 and parabolic variation
means:
and parabolic variation
means: 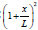
Notice the color significance in (Figure 3, Figure 4, & Figure
5); The blue color represents the results of a one-dimensional element with constant inertia and material ( I =1, G =1, and ρ =1). As for the red color, it represents the results of the onedimensional
element with linear variation in Inertia (Figure 3)
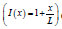
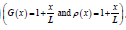 And finally,
the black color represents the results of the one-dimensional element with parabolic variation in Inertia (Figure 3)
And finally,
the black color represents the results of the one-dimensional element with parabolic variation in Inertia (Figure 3) 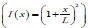 or in material (Figure 4)
or in material (Figure 4) 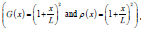 As for the line styles,
the solid line represents the 1 mode shape, the dotted represents
the 2nd mode shape and the dashed represents the 3rd mode
shape. As shown in the (Figures 3, 4 & 5), on increasing the crosssection’s
stiffness, the maximum relative angular deformation
(twist) decreases. It is also observed that the linear variation in
inertia gives approximately the same maximum relative angular
deformation (twist) as that of the material variation and the same
thing can be applied to the parabolic variation.
As for the line styles,
the solid line represents the 1 mode shape, the dotted represents
the 2nd mode shape and the dashed represents the 3rd mode
shape. As shown in the (Figures 3, 4 & 5), on increasing the crosssection’s
stiffness, the maximum relative angular deformation
(twist) decreases. It is also observed that the linear variation in
inertia gives approximately the same maximum relative angular
deformation (twist) as that of the material variation and the same
thing can be applied to the parabolic variation.
Analysing the obtained natural frequencies in (Table 2), it is observed that the linear variation in the cross-sectional inertia gives approximately the same effect as that of the linear change in material. Furthermore, the parabolic variation too gives approximately the same effect on changing the inertia only or the material only while keeping the other parameter constant. The linear variation in both at the same time produces the same effects as those of the parabolic variation of either of them.
Summary and Conclusion
This study illustrated the use of the DQM in torsional vibration problems and validated its reliability in calculating the free undamped torsional natural frequencies & mode shapes of onedimensional elements. In addition to this, a parametric study was successfully carried out depicting the effects of End conditions, cross-sectional variation (Moment of inertia), & material variation (Shear Modulus & density) on the torsional natural frequencies and the corresponding mode shapes. The proposed solution method showed great agreement with the analytical solution of the basic beam torsional vibration problem which made it encouraging to try different parameters and compare the results with our so-called control beam solved analytically. As shown in (Table 1), the natural frequencies increase by increasing the mode number in an end-condition. It is also noted that the linearly varying inertia gave approximately the same results of linearly changing the material and it is the same in case of the parabolic variation. In addition to that, it is noted that making a linear change in both of the material and the inertia gave the same results as those obtained from changing only one of the two parameters linearly.
References
- Adams DE (2010) Mechanical vibrations. pp: 1-131.
- Zhang WM, Wang ZW, Zhang HQ, Lu XF, Liu Z (2020) Analytical study on free vertical and torsional vibrations of two- and three-pylon suspension bridges via d’Alembert’s principle. Structural Engineering and Mechanics 76(3): 293-310.
- Adekanye O, Washington T (2018) Nonstandard finite difference scheme for a Tacoma Narrows Bridge model. Applied Mathematical Modelling 62: 223-236.
- Rao SS (2011) Mechanical vibrations. Prentice Hall.
- Pouyet JM, Lataillade JL (1981) Torsional Vibrations of a shaft with non- uniform cross section.
- Li QS (2003) Torsional vibration of multi-step non-uniform rods with various concentrated elements. Journal of Sound and Vibration 260(4): 637-651.
- Rafiee M, Mehrabadi SJ, Rasekh-Saleh N (2010) Analytical solutions for the torsional vibrations of variable cross-section rods 2(4): 64-71.
- Rezeka SF (1989) Torsional Vibrations and Design Charts for Hollow Shafts with Variable Cross Section.
- Basu AK (1982) Dynamic characteristics of coupled wall-frame systems.
- Miranda E (1999) Approximate seismic lateral deformation demands in multistory buildings.
- Miranda E, Taghavi S (2005) Approximate Floor Acceleration Demands in Multistory Buildings. I: Formulation. Journal of Structural Engineering 131(2): 203-211.
- Taghavi S, Miranda E (2005) Approximate Floor Acceleration Demands in Multistory Buildings. II: Applications. Journal of Structural Engineering 131(2): 212-220.
- Zalka KA (2014) Maximum deflection of asymmetric wall-frame buildings under horizontal load. Periodica Polytechnica Civil Engineering 58(4): 387-396.
- Zalka (2009) A simple method for the deflection analysis of tall wall-frame building structures under horizontal load. Structural Design of Tall and Special Buildings 18(3): 291-311.
- Piccardo G, Tubino F, Luongo A (2015) A shear-shear torsional beam model for nonlinear aeroelastic analysis of tower buildings. Jitscript fur is a mathematician and a physicist 66(4): 1895-1913.
- Annibale DF, Ferretti M, Luongo A (2019) Shear-shear-torsional homogenous beam models for nonlinear periodic beam-like structures. Engineering Structures 184: 115-133.
- Luongo A, Zulli D (2020) Free and forced linear dynamics of a homogeneous model for beam-like structures. Meccanica 55(4): 907-925.
- Piccardo G, Tubino F, Luongo A (2016) Equivalent nonlinear beam model for the 3-D analysis of shear-type buildings: Application to aeroelastic instability. International Journal of Non-Linear Mechanics 80: 52-65.
- Greco A, Fiore I, Occhipinti G, Caddemi S, Spina D et al. (2020) An equivalent non- uniform beam-like model for dynamic analysis of multi-storey irregular buildings. Applied Sciences (Switzerland) Volume 10, Issue 9.
- Bellman R, Casti J (1971) Differential Quadrature and Long-Term Integration.
- Wilson EL Inc (2000) Three dimensional static and dynamic analysis of structures: A physical approach with emphasis on earthquake engineering. Computers and Structures.
- Maher Sabah Abdulmahdi, Sabah Abdulmahdi Al M (2012) Effect of shear moduli and modular ratio (G F /G M) on the natural frequency of fiber reinforced composite rod under torsional free vibration.
- Lopes Gama A, Soares De Oliveira R (2014) An Algorithm for Solving Torsional Vibration Problems Based on the Invariant Imbedding Method.
- Rajasekaran S (2009) Structural Dynamics of Earthquake Engineering Theory and Application using Mathematica and Matlab. Woodhead.
- Shu C (2000) Differential Quadrature and Its Application in Engineering, Differential Quadrature and Its Application in Engineering.






























