Research Article

On Approach of Analysis of Oscillations of a Multilayer Structures

Pankratov EL^1,2*

¹Nizhny Novgorod State University, 23 Gagarin avenue, Nizhny Novgorod, 603950, Russia

²Nizhny Novgorod State Technical University, 24 Minin Street, Nizhny Novgorod, 603950, Russia

Submission: June 23, 2020; Published: January 15, 2021

*Corresponding Author:Pankratov EL, Nizhny Novgorod State University, 23 Gagarin avenue, Nizhny Novgorod, 603950, Russia

How to cite this article: Pankratov EL. On Approach of Analysis of Oscillations of a Multilayer Structures. Civil Eng Res J. 2021; 11(2): 555808. DOI:10.19080/CERJ.2020.11.555808

Abstract

In this paper we analyzed sound influence on a multilayer building structures with increasing sound insulation on the example of oscillations of a multilayer plate. An analytical approach for analyzing the data of oscillations has been introduced.

Keywords:Climatization systems; Sanitary hot water; Energetic certification of buildings

Abbreviations: SHW-Sanitary Hot Water

Introduction

High rates of development of construction equipment create the necessary prereq-uisites for the design and construction of buildings and other structures of elements that have significant strength and stability with low weight and small thickness [1-5]. At the same time, the development of technology leads to the emergence of more powerful machines and to increasing number of vehicles, which leads to increasing of noise in populated areas, civil and industrial buildings. Acoustic improvement of premises becomes an actual problem of each design and construction of each building [6-9]. Framework solving this problem, the problem of the sound-insulating ability of the enclosing and supporting structures is first of all solved. To solve the problem, it is necessary to analyze the sound effect on the structure. Framework the paper, an analysis of this effect has been done, considering the possible multilayered structure. We will analyze this effect using the example of transverse oscillations of a multilayer plate (structure) due to the action of a plane sound wave perpendicular to the interface between the layers of the plate.

Method of solution

The oscillation of the plate is determined by solving the following wave equation

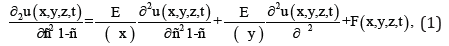
where Eis the modulus of elasticity; ñis the density of the plate materials; σis the Poisson ratio, u(x,y,z,t)is the displacement of the points of the plate when it oscillates; F(x,y,z,t) is the external impact (impact, sound wave, etc.); L_x, L_y and L_z are the dimensions of the plate in the directions indicated in the indices; x, y and z are spatial coordinates; t is time. Let us consider the case when the edges of the plate are rigidly fixed and there is no effect on it at the time of the beginning of its consideration. Then the boundary and initial conditions for equation (1) could be written in the following form

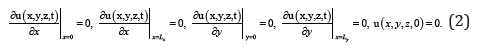
Now we solve the Eq.(1) using the method of averaging functional corrections [10]. In the framework of this method, in order to obtain the first approximation of the desired function u(x,y,z,t) replace it with the unknown average value 1α in the right-hand side of the Eq.(1). Then the equation for the first approximation of the function u(x,y,z,t) takes the form

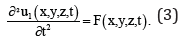
The solution of Eq. (3) is represented in the following form

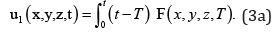
The average value of the function u(x,y,z,t) is determined using the standard relation

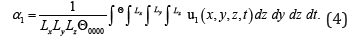
where Θ is the duration of observation of the oscillation of the considered plate. Substitution of the relation (3a) into (4) leads to the following result

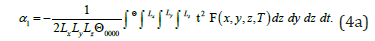
The second-order approximation of the function u (x,y,z,t) is determined by replacing it in the right-hand side of the Eq. (1) by the sum of the approximation of the previous order and the mean value of the desired approximation 2 α , i.e. by the amount α₂ + u₁(x,y,z,t). Then the equation for the second approximation of the function u(x,y,z,t) takes the form

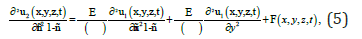
Solution of the Eq. (5) could be written as

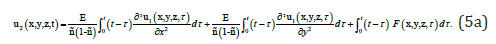
The average value 2 α of the second-order approximation of the function u(x,y,z,t) is determined using the standard relation [10]

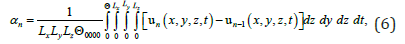
where n is the order of the required approximation. Substitution of relations (3a) and (5a) into (6) leads to the following result

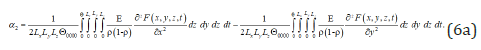
An analysis of the spatiotemporal distribution of the displacement of the plate points during its oscillation has been done analytically framework the second order approximation by the method of averaging the functional corrections. The approximation is usually enough for qualitative analysis and obtaining some quantitative results. The results of the analytical calculations were verified by comparing them with the numerical results.

Discussion

In this section, we will analyze the space-time distribution of the displacement of the points of the plate when it vibrates under the action of a plane wave F(x,y,z,t) = A.exp (k_zz−ωt ), where A is the amplitude of the wave, k_z is the projection of the wave number on the Oz axis, and w is the wave frequency. Figure 1 shows the qualitative spatial distribution of the displacement of the points of the plate as a function of the coordinates x and y at a fixed time. Figure 2 shows the qualitative spatiotemporal distribution of the displacement of the plate points as a function of the coordinate z and time t for fixed values of the x and y coordinates.

Conclusion

In this paper, we propose an analytical approach for analyzing plate vibrations un-der the influence of external action. As an example of such an impact, sound impact is possible. The proposed analytical approach allows us to consider the multilayeredness of the plate under consideration.

References

1. Long L, Kang H, Mo R. KSCE Journal of Civil Engineering. 21(1): 178-183.
2. Xue H, Jian Zhang S. KSCE Journal of Civil Engineering. 21(5): 1606-1613.
3. Pisal AY, Jangid RS International Journal of Advanced Structural Engineering. 8(2): 213-227.
4. Zhang C, Zayed T, Hijazi W, Alkass S Open Journal of Civil Engineering.6(3): 442-461.
5. Gong Z, Zeng B, Han W, Xue S Open Journal of Civil Engineering. 7(2): 303-310.
6. BroujerdianEmail V, Kaveh A, Rahmani M Asian Journal of Civil Engineering.19(6): 693-701.
7. Nayak AN, Satpathy L, Prasant K International Journal of Advanced Structural Engineering10(2): 153-167.
8. Long NV, Quoc TH, Tu TM 8(4); 391-399.
9. Tran MT,Nguyen VL, Trinh AT International Journal of Advanced Structural Engineering. 9(2): 153-164.
10. (1955) YuDSokolov. Applied Mechanics. 1(1): 23.