Review Article

A Set of Shaking Table Model Tests of Seismic Hydrodynamic Pressure on Bridge Pier with Submerged Depth

Hai-ming LIU¹, Xia-xin TAO²*, Zheng-ru TAO³ and Yi-fang QIN³

¹State Key Laboratory of Bridge Engineering Structural Dynamics, China Merchants Chongqing Communication Research & Design Institute Co., Ltd, Chongqing, 400067, China

²School of Civil Engineering, Harbin Institute of Technology, Harbin, 150036, China

³Institute of Engineering Mechanics, CEA, Harbin, Heilonjiang, 150080, China

Submission: November 20, 2020; Published: December 03, 2020

*Corresponding Author:Xia-xin TAO, School of Civil Engineering, Harbin Institute of Technology, Harbin, 150036, China

How to cite this article: Hai-ming L, Xia-xin T, Zheng-ru T, Yi-fang Q. A Set of Shaking Table Model Tests of Seismic Hydrodynamic Pressure on Bridge Pier with Submerged Depth. Civil Eng Res J. 2020; 11(1): 555804. DOI 10.19080/CERJ.2020.11.555804

Abstract

A set of shaking table model tests of hydrodynamic pressures on bridge piers are presented in this paper. Five models made of Perspex and concrete with rectangular, elliptical and variable sections are built, and fixed in a steel tank on shaking table with 0.9 m to 1.6 m water, respectively. The seismic hydrodynamic pressures observed at 4/7/8 submerged depths from two level inputs of ground motions and two direction combinations show that the representative values per unit area increase with submerged depth obviously, the increasing rate is generally faster than those by the two classical assumptions at shallow depth, but slower at deep depth.

Keywords: Seismic hyadrodynamic pressure; Model test; Shaking table; Submerged depth

Introduction

The effect of hydrodynamic pressure on bridge pier is required to combined with those from ground motion, dead load, earth pressure and so on in seismic design, according to the Seismic Design Code of Highway Bridges of China[1], as well in Japanese [2] and European codes [3]. In the last two decades, many bridges have been constructed in deep water worldwide, with water depth even more than 100 m, especially in China. A new pressing issue must be answered by scientists is that if the effect increases with water depth significantly and how fast it may increase. The first classical formula of hydrodynamic pressure during earthquake was presented by Westergaard in 1933 for the case of a straight dam with a vertical upstream face [4]. It was derived by a simplification from Fourier series solution of the wave motion equation with a quadratic parabola for the general shape of the pressure distribution diagram with vertical axis. In the simplification, the curve is satisfied the condition of a horizontal tangent at the water surface, but not satisfied the other one of a vertical tangent at the dam bottom, since the parabola has a sloping tangent at the bottom. In 1965, Goto and Toki presented a formula for the pressure on a cylindrical submerged bridge pier during earthquake [5], a cubic expression was chosen by means of shaking table model experiments with three cylinders and one column with simple harmonic motion inputs. This formula was adopted by Japanese Design Specifications for Highway Bridges [6], and then by Chinese Specifications of Earthquake Resistant Design for Highway Engineering [7]. Therefore, the vertical distribution of hydrodynamic pressure with submerged depth governs the formula in our design code, and it is very important in improvement of the formula, although that distribution of pressure on pier could not be revealed theoretically. At present, there are two ways to improve the understanding of the pressure distribution during earthquake, model test on shaking table and numerical simulation. The former could reveal the dynamic interaction nature between water and pier during ground motion, but is expensive and time consuming, and is limited by the size of the table. The latter is cheap and fast but is limited to the dynamic mechanism adopted in the calculation. A feasible approach is to combine the two. Many results of numerical studies on seismic hydrodynamic pressure on bridge pier have been published in the past two decades, while just few tests were carried out, especially on distribution of the pressure with submerged depth [8-12]. To study the variation of the pressure with submerged depth in deep water, a set of shaking table model tests were carried out recently [13,14]. In this paper, design and details of the tests are reported, and the results from the test are presented. The curves of the seismic hydrodynamic pressure distribution with submerged depth are analyzed and compared with the assumptions of the two classical references respectively.

Bridge pier models and sensor layout in the tests

There are totally five models, one is 1/50 scaled pier of a cable-stayed bridge in south-western region of China with total height of 4.54 m, made of Perspex, consists of the pylon limb and hollow rectangular cross-section with thickness 0.03 m and outer section 0.70 m×0.31 m, another model is for pier of a rigid frame bridge with two limbs also made of Perspex, size of each limb is 0.13~0.20 m× 0.06 m × 1.80 m in length, width and height, and the other three are concrete pier models with sections of rectangular, elliptic and variable rectangular (in brief variable, below) respectively, all made of C50 concrete and HRB 400 rebar. The size of rectangular pier model is 0.50 m × 0.30 m × 2.89 m in length, width and height; that of elliptic section model is 0.48 m × 0.31 m × 2.87 m in major axis, minor axis and height; the width and height of the variable section pier model are 0.30 m and 3.19 m, and the length is from 0.31 m at the top to 0.62 m at the bottom. The Perspex model is built with Young’s modulus of 3.11GPa, tensile strength reaching 78.3Mpa and density of 1200kg/m3. The elastic modulus, Poisson’s ratio, and mass density are 34.5 GPa, 0.2 and 2500 kg/m3 for C50 concrete, and 210 GPa, 0.2 and 7850 kg/m3 for the rebar, respectively

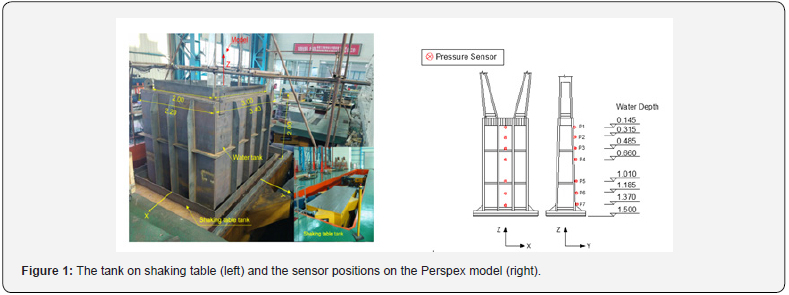
The technical parameters of the shaking table and the similarity ratios of the models for the tests are listed in Table 1 and Table 2. Each of the pier models is fixed in a rectangular steel tank with a dimension of 2 m×3 m×2 m in the test, in water with depth of 1.1 m and 1.6 m for concrete model, and 0.9 m and 1.5 m for the Perspex one, as shown in Figure 1 (left). Some wave absorbing stuff are put on the four lateral inner walls of the tank to reduce reflected wave. CY202 micro hydrodynamic pressure sensors are fixed at seven/eight heights along the vertical central line of upstream face of the pier model, as an example, the sensors layout on the Perspex model is shown in Figure 1 (right). The measurement range is 0 to 100 kPa with precision ±0.1% and sampling rate 100 per second. RS485-20 smart data acquisition system is adopted to record water pressure time histories at those depths in each test.

Inputs and observed pressures in the tests

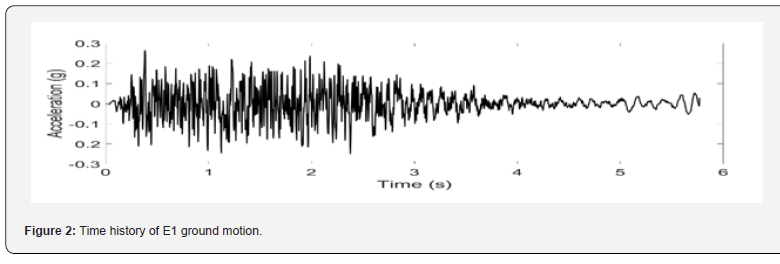
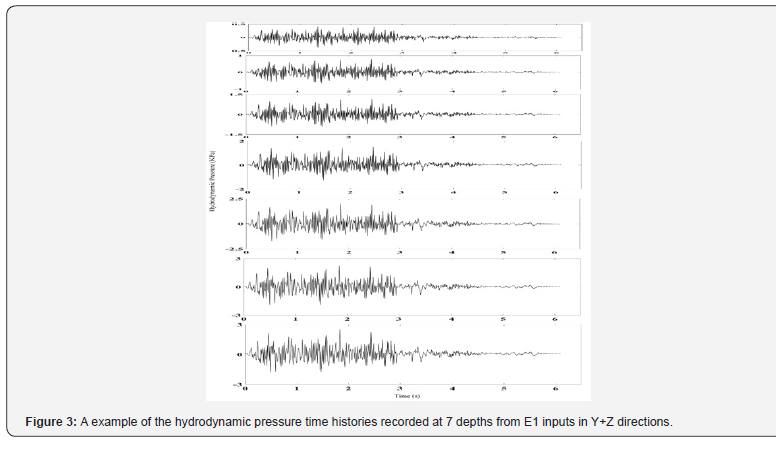
The hydrodynamic pressures at 4 sensors emerged in 1.1m and 7 sensors in 1.5 m water are recorded from E1 and E2 inputs of ground motion time histories up to 6 seconds with horizontal peak acceleration 0.265g and 0.51g in longitudinal and half of them in vertical directions (X+Z, in brief), and in transverse and vertical directions (Y+Z) respectively, and at the all 8 sensors in 1.6m water are recorded only from E1 input. As an example, time history of E1 motion is shown in Figure 2.

Distribution of hydrodynamic pressure with submerged depth from the tests

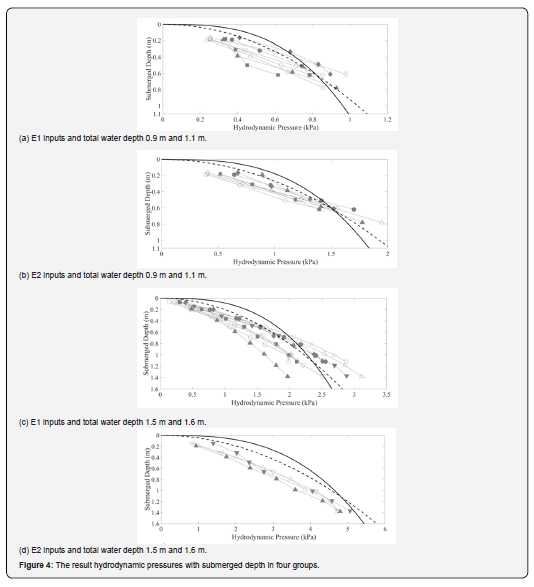
A preliminary comparison between the pressures from tests with different total water depths, inputs, and pier models show that the pressures increase with submerged depth with a similar rate for all pier models, input direction combinations [11]. The pressures from stronger input are always lager, and similarly from the total water depths. Therefore, the result hydrodynamic pressures are analyzed in four groups, two from E1 input and two from E2 input, with total water depth 0.9 m to 1.1m and 1.5 m to 1.6 m respectively. The curves of the In the figures, the symbols of small square, circle, diamond are for the pressures on the concrete pier models with rectangular, elliptical, variable sections, and regular and inverted triangles are for those on the Perspex pier models with hollow rectangular and two limbs sections, respectively. The symbols stuffed in dark grey are for the pressures from X+Z input direction combinations, and the hollow are from Y+Z inputs. All symbols of the pressure in each test are linked with thin grey lines and compared with the black curves from the assumptions in above mentioned two classical references. The solid curve is from the cubic expression, while the broken curve is from the quadratic parabola. One can see from the Figure 4 that the increasing rate of pressures with the submerged depth is generally faster than those by the classical assumptions in [5,4] at shallow depth, but slower at deep depth.

Conclusion

A set of shaking table tests of hydrodynamic pressures on five pier models made of Perspex and concrete with rectangular, elliptic and variable sections, in 0.9 m to 1.1 m and 1.5 m to 1.6 m water respectively are presented. The observed results from inputs of two leverl ground motion time histories and two direction combinations show that the representative values of hydrodynamic pressure per unit area increase with submerged depth obviously, the increasing rate is generally faster than those by the two classical assumptions at shallow depth, but slower at deep depth. The result arouse the authors to study the situation at very deep depth by numerical simulation approach. Of course, the unit depth hydrodynamic pressure or whole pressure on the upstream face of pier stipulated in seismic design code can be studied by integrated horizontally from the distribution of this per unit area pressure, and then by secondary integral vertically.

Acknowledgements

The authors sincerely appreciate Dr. Geng for his hosting of the tests in State Key Laboratory of Bridge Engineering Structural Dynamics, China Merchants Chongqing Communication Research & Design Institute Co., Ltd.

Funding

This study is financially supported by 201701 of open funds of State Key Laboratory of Bridge Engineering Structural Dynamics and Key Laboratory of Bridge Earthquake Resistance Technology, Ministry of Communications, PRC, and grants of 51678540 and 51778197 of National Nature Science Foundation of China.

References

1. Ministry of Transport of the Peoples Republic of China. Guidelines for seismic design of highway bridges (JTG/T B02-01-2008).
2. (2012) Japan Road Association. Design Specifications for Highway Bridges, Part V Seismic Design.
3. (2011) Technical Committee CEN/TC250. Euro code 8: Design of structures for earthquake resistance –Part 2: Bridges.
4. Westergaard HM (1933) Water pressures on dams during earthquakes. Trans Asce 98(2): 418- 433.
5. Goto H, Toki K (1965) Vibrational characteristics and aseismic design of submerged bridge piers. Pro. of the 3rd World Conference on Earthquake Engineering. New Zealand.
6. (1980) Japan Road Association. Design specifications for highway Bridges, Part V Seismic Design.
7. (1989) Ministry of Transport of the People's Republic of China. Specifications of earthquake resistant design for highway engineering (JTJ 004-89).
8. Lai L et al (2006) The shaking table test for submerged bridge pier. Earthquake Engineering and Engineering Vibration, 26(4): 164-171.
9. Song B, Zhang G (2010) Shaking table test of pier-water interaction. Journal of University of Science and Technology Beijing, 32(3): 403-408.
10. Liu C, Zhang J, Zhang S (2016) Model test on the underwater shaking table for the tower of deep-water cable-stayed bridge. Journal of Water Resources and Architectural Engineering.
11. Ding Y, Ma R, Shi YD, Li ZX (2017) Underwater shaking table tests on bridge pier under combined earthquake and wave-current action. Marine Structures 58: 301-320.
12. Zhi Z, Xiaojun Li, Riqing L, Chenning S (2018) Shaking table tests and numerical simulations of a small radius curved bridge considering SSI effect. Soil Dynamics and Earthquake Engineering 118(12): 1-18.
13. Liu H, Tao X, Tao Z, Qin Y (2019) Preliminary result of seismic hydrodynamic pressure on bridge pier with depth in water from a shaking table test. Earth and Environment Science 453:288-293.
14. Liu H, Tao X, Tao Z, Qin F (2020) Seismic hydrodynamic pressure on concrete bridge pier with submerged depth from a set of shaking table model tests. Journal of Physics: Conference Series 1624: 022019.