Research Article

Buckling Analysis of Guyed Composite Transmission Poles

Sriram Kalaga¹*, Prema Kumar WP², Supreeth AR³ and Mahendra Kumar P⁴

¹Consulting Structural Engineer, Glen Burnie, USA

²School of Civil Engineering, Reva University, India

³Department of Civil Engineering, Global Academy of Technology, India

⁴Royota Engineering, Pvt Ltd., India

Submission: September 30, 2019; Published: October 22, 2019

*Corresponding Author:Sriram Kalaga, Consulting Structural Engineer, Glen Burnie, USA

How to cite this article: Sriram Kalaga, Prema Kumar WP, Supreeth AR, Mahendra Kumar P. Buckling Analysis of Guyed Composite Transmission Poles. Civil Eng Res J. 2019; 9(3): 555762. DOI: 10.19080/CERJ.2019.09.555762

Abstract

The buckling loads of guyed modular composite (FRP) transmission poles of various heights and classes are computed using the Gere and Carter Method (GCM) and Linear Buckling Analysis using ANSYS finite element software. Four (4) specific end conditions are investigated: fixed-free, fixed-pinned, pinned-pinned and fixed-fixed ends. To simplify calculations, average values of elastic modulus E and tube thickness t are employed. The buckling loads obtained by the two methods are compared. Given the approximations used in the modelling process, it is observed that there is reasonable agreement between the values for buckling loads obtained by two approaches for all the end conditions, the maximum average discrepancy being about 24.3%. Suggestions for further studies include modelling each pole module explicitly with its specific properties and conducting full-scale lab testing to validate all studies.

Keywords: Buckling, Convergence, End conditions, Finite element, Guyed, Pole, Transmission, Composite

Notation: d = diameter; da = diameter at point of guy attachment ; dg = diameter at ground line; de = diameter at pole butt; fb = failure stress of pole module; k = effective length factor; De = depth of embedment; E = modulus of elasticity; Eave = average modulus of elasticity (Table 3); I = moment of inertia; IA = moment of inertia at A; L = length of pole or column; LAG = height of pole above ground; P* = multiplier in Equation (2); PA = critical load for a uniform column of diameter d; Pcr = critical buckling load; PE = Euler buckling load; t = wall thickness; tave = average wall thickness (Tables 1); α = exponent in Equation (3)

Introduction

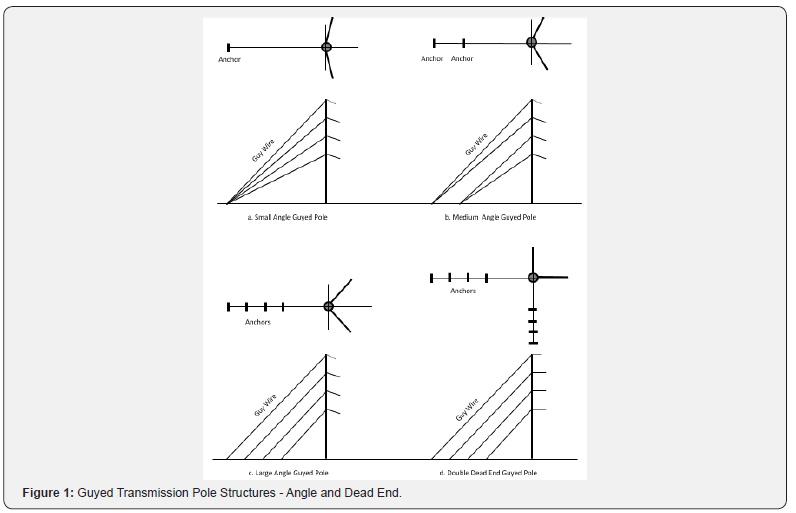
Guyed transmission poles are commonly used in transmission lines at turning angle locations and at dead ends (Figure 1). Although guying is routinely employed in wood pole systems owing to a lack of bending strength of wood, it is also occasionally used for poles of other materials too such as steel, concrete, laminated wood and composite or FRP [1]. As can be seen from Figure 1, the purpose of the guy wires is to back up the wire tension resultants from the conductors and the ground wires and transmit them to the anchors. Figure (1a) shows a single anchor associated with all four guy wires; but (1b) and (1c) show multiple anchors. Bending moments in the pole are generally minimal since each guy location acts as a partial lateral support, restraining movement in a specific direction. A single set of guy wires can be adequate for small line angles depending on the imposed wire tensions. But a 90o dead end shown in Figure (1d) requires guys and anchors in both orthogonal directions. The most common slope for a guy wire is 45 degrees. One result of the guy wire tensions is the ver tical load component at each guy location and this component – cumulative for multiple guy wires – acts as an axial load on the pole column. For 90o dead ends the axial loads come from both directions. Therefore, design involves check for pole buckling [2]. From analysis perspectives, a transmission pole is basically a beam-column with constantly varying cross section from base to top. Design of guyed poles in USA is governed by various codes and standards [3, 16]. Since composites are not a bio-degradable material and rather stable in physical and other properties, there is no need to impose any strength reduction factor in design, unlike wood while computing load capacities [3].

Past research included several landmark studies on guyed poles, including the Finite Element Method (FEM). Non-linear stiffness matrices were developed for various shapes; but little effort was made to systematically analyze guyed poles of different structural materials. In addition to round wood, guyed transmission poles currently include tubular steel, pre-stressed concrete, laminated wood and fiber-reinforced polymer (composite) poles. This study is part of an undertaking towards that larger goal which comprises several papers on guyed transmission poles. The aim of this paper is to investigate the buckling behavior of guyed composite transmission poles employing the FEM and verify the values of the buckling loads with theoretical estimates. A set of 15 composite poles representing the most common sizes and classes of poles utilized in guying situations, together with four kinds of end conditions, were considered. Only linear elastic buckling is studied. Although initial out-of-straightness is often important in buckling patterns, it is not considered here. This paper is intended to be the last part of a series of papers on guyed poles; others are on round wood, tubular steel, pre-stressed concrete, and laminated wood poles.

Literature Review

Theoretically, a transmission pole of any material is a tapered beam-column with constantly varying cross section from base to top. As such, analytical modelling involves the challenge of incorporating stiffness matrices into analysis algorithms. A significant amount of work had been directed therefore towards formulating finite element stiffness matrices to handle tapered beam-columns [4-11] and buckling of FRP poles [12,13]. The earliest study on tapered beam-columns is contained in the classic 1968 paper by Gere and Carter [14] where expressions were derived for the buckling strength of various steel beam-columns for different end conditions. This study provided the foundation for estimating the buckling capacity of poles.

Peabody and Wekezer [15] investigated the buckling strength of transmission and distribution poles using the FEM. Buckling capacities were determined with an Eigenvalue approach using elastic and geometric stiffness matrices of beam elements. One important conclusion drawn in this study is that assuming the unbraced length of the beam-column as the distance from the lowest guy to the ground can lead to a dangerous overestimation of the buckling strength. This implies that a more rational approach would be to consider the entire pole above the ground as a candidate for buckling. The ASCE Manual 91 [16] is another design reference for guyed transmission structures. This Manual also refers to the Gere-Carter Method and discusses the difficulties associated with real-life boundary conditions. Idealized end conditions rarely exist in real poles. An important point made in the Manual is that most theoretical methods, including the Gere-Carter Method, lead to large errors in situations where the capacity of the pole is controlled by bending stresses amplified by large compressive loads (i.e.) a true nonlinear beam-column behavior. Based on a nonlinear finite element analysis of a guyed pole, including guy wires modelled as cable elements, it is shown that theoretical estimates are ½ to 2½ times that predicted by the FEM. It is therefore left to the design engineer to adopt a reasonable factor of safety in using theoretical procedures. The RUS Bulletin 153 [20] also contains another procedure to compute elastic buckling loads of wood poles. It is based on the approach used in timber construction which suggests that the critical section for a guyed wood pole is located at 2/3 the distance of from the ground to the bottom- most guy attachment. It also recommends a minimum factor of safety of 1.50 to be applied to the computed loads. Subsequent studies suggested that the RUS procedure is more conservative than the Gere-Carter Method (GCM).

Commercial computer programs such as PLS-Pole [22] include both the GCM and RUS options for users.

despite a number of theoretical and analytical investigations, no full-scale tests were performed to confirm and generalize the observations from those studies. There is also little evidence that modular poles composed of segments of different moduli of elasticity ‘E’ were studied with reference to buckling

End Conditions of Guyed Poles

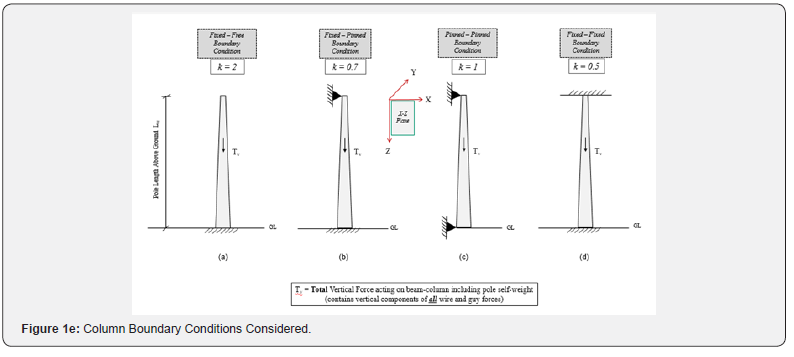
IEEE 751 [21] discusses the issue in detail. The end restraints in guyed poles are difficult to evaluate. Poles with bi-sector guys, as seen in Figure 1a, 1b and 1c, approximate a condition of being pinned at the point of guy attachment and fixed at the base, in plane of the guy wire. However, at 90 degrees to this plane, the pole is basically a free cantilever. Also, it is generally believed that the conductors also offer some kind of restraint. Therefore, the overall effective boundary conditions may be between the fixedfree (k = 2) and fixed-pinned (k = 0.7). For a 90o degree guyed dead end shown in Figure 1d, the fixed-pinned condition occurs in both planes (k = 0.7). Some engineers question whether the guy wires restrain lateral motion sufficiently to justify a k value of 0.7. Due to this, routine designs assume k = 1 although a value of 0.80 is often suggested. (Figure (1e) for configuration of various boundary conditions).

Euler’s Elastic Buckling Theory

A column is considered stable only if the critical elastic buckling load (or Euler load) is not exceeded. The elastic buckling load of a column is defined as the axial load that is just enough to keep an initially straight, perfectly elastic bar in a slightly bent form. This load is usually taken as the ultimate load that the column can support, assuming the column is relatively slender and buckling occurs in the elastic range. The Euler’s critical buckling load for long slender columns of uniform section is given by:

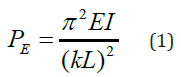
where

PE = critical buckling load

k = effective length factor

L = actual length of column

E = modulus of elasticity of column material

I = least moment of inertia of the column cross-section

Equation (1) is obviously applicable only to uniform-section, homogenous columns where the axial load is concentrically applied at the end of the column. This assumption is not valid for a guyed tapered pole: constantly varying cross section aside, a typical guyed transmission pole has axial loads from guy wires are applied intermittently at various heights along the pole. Hence Euler theory cannot be directly used for such poles.

Gere and Carter Method

The Gere and Carter Method (GCM) [14] is commonly used in practice for calculating critical buckling loads for guyed tapered wood poles. This method proposes modification to the Euler’s critical buckling equation as follows:

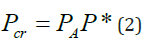
where:

PA = Critical load for a uniform column with circular sections having diameter d (at guy attachment)

P* = A multiplier dependent on the end conditions of the column

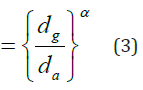
where

α = An exponent that is a function of shape of the column

da= Diameter at point of guy attachment

dg= Diameter at the ground line

L = Distance from ground line to the point of guy attachment

Equations for various end conditions for a tapered wood pole are summarized in Table 1.

The Gere and Carter Method assumes the column to be initially straight, homogenous, elastic and compressed by an axial load. It is a theoretical method verified by limited tests on steel shapes for tapered poles subject to only axial load. The method apparently is not intended for situations where material properties of the pole changes with length. When using this method for NESC ice and wind loads [3] with specific load factors, it is recommended to use a factor of safety between 2.50 and 3.0. For extreme wind loads, where all load factors are 1.0, the resulting factors of safety will be between 1.5 and 2.0. For pure dead ends, higher safety factors must be used due to larger axial loads.

Application to Selected Composite Poles

As opposed to round wood poles where the cross section is solid and round, all composite (FRP) poles are round but tubular with a specific wall thickness which varies from a minimum of 3/8 inch (9.5 mm) and above [17]. Modular tube arrangements come with different wall thicknesses (‘t’) for different modules within the same pole, as well as different material properties (modulus of elasticity ‘E’ and failure stress ‘fb’). Fifteen FRP composite poles from RS Poles [18] ranging in length from 50 ft. to 70 ft. (15.2 m to 21.3 m), involving several pole classes and four (4) specific boundary conditions are studied. This set of 15 poles represents common sizes of poles utilized in the industry. The definition of a pole class is illustrated in Figure 2 while Table 2 shows the numerical values of lateral loads associated with composite pole classes [2,18].

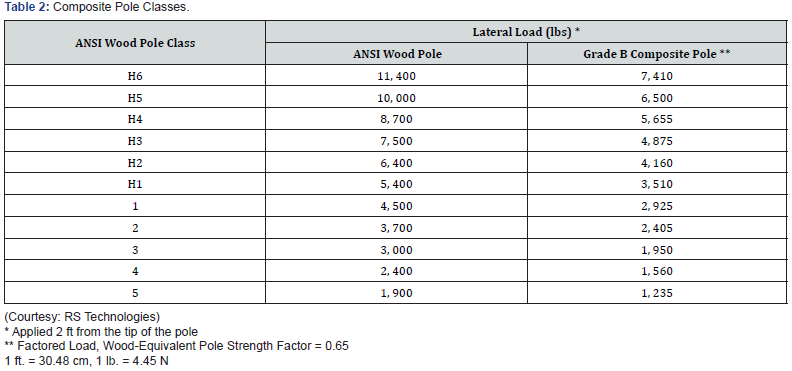
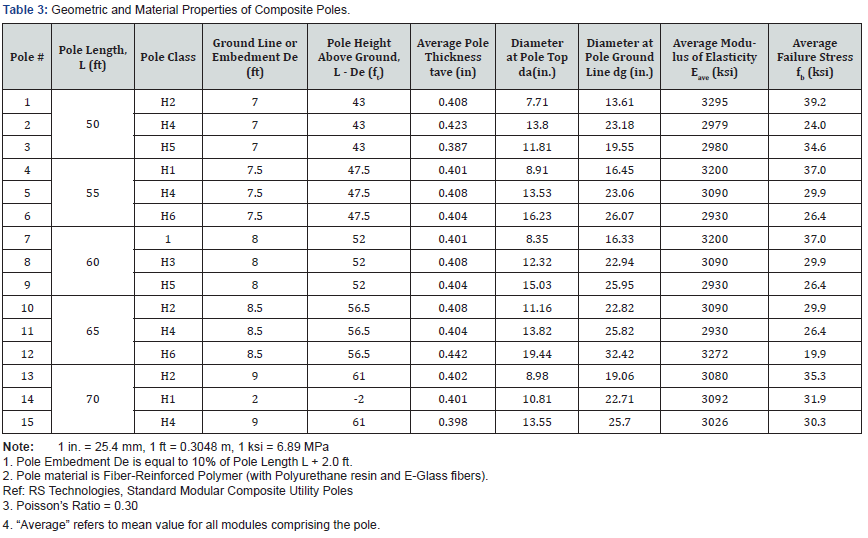
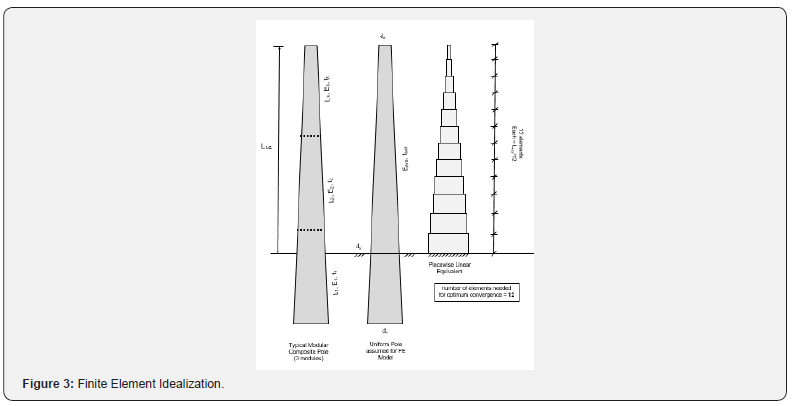
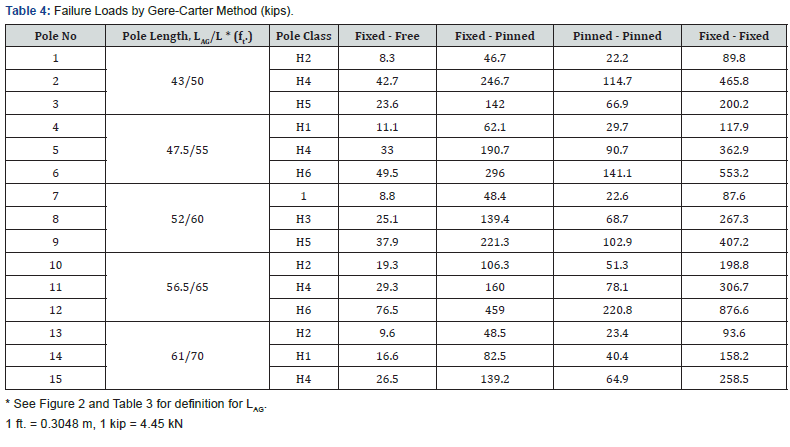
All selected poles are modular with varying number of modules (2 to 5) and with each module having a different bulk or global E and t. The pole material is filament-wound FRP – with Polyurethane resin and E-Glass fibers. Geometrical and material design properties of these poles are shown in Table 3. To simplify modelling and computations, and to enable application of GCM and subsequent comparisons between GCM and FEM, an average value of bulk modulus of elasticity E and t were used for all poles (Figure 3). This approach corresponds to the “global” or “quasi- isotropic” method outlined in the RS Poles design guide [18]. It must be noted that the bulk material properties are a function of loading and type of structural system; but as long as the response remains linear, a single or average value may be used, subject to the applicable limitations. The values of the critical buckling load obtained by the Gere and Carter Method are given in Table 4. These values are computed using a custom spreadsheet developed for the purpose. In all cases, the effective length for buckling is taken as the pole height above ground LAG.

Buckling Analysis using FEM

In the present study, ANSYS software [19] is used to perform linear or classical finite element buckling analysis of tapered composite poles. The finite element used is a Beam-188 element that has two end nodes with 3 translational and 3 rotational degrees of freedom at each node. This element is based on Timoshenko beam theory, includes shear deformation effects, well-suited for both linear/non-linear applications and flexural, lateral and torsional stability (using Eigenvalue buckling) problems. All FE models are planar beam-columns in the X-Z plane (with out-of-plane movement restrained (Figure 1e).

Convergence Study

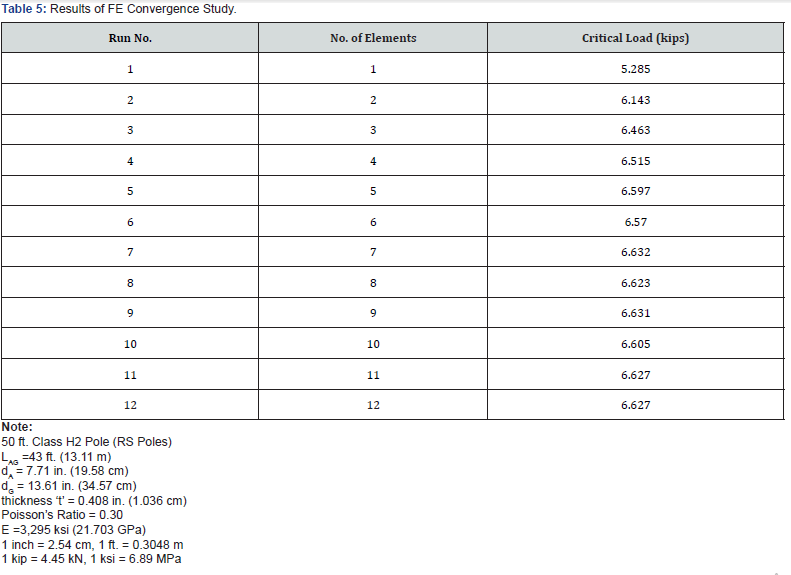
A convergence study was made to determine the number of elements which yields accurate result. A tapered composite pole was discretized using uniform two-node Beam 188 elements. The results are provided in Table 5 for fixed-free end conditions, indicating that 12 elements would give sufficiently accurate result for buckling load. Hence, in all further work, a finite element model having 12 elements is used. (In comparison, Peabody and Wekezer used 14 equal length beam elements in their FE studies).

Buckling Loads from FEM

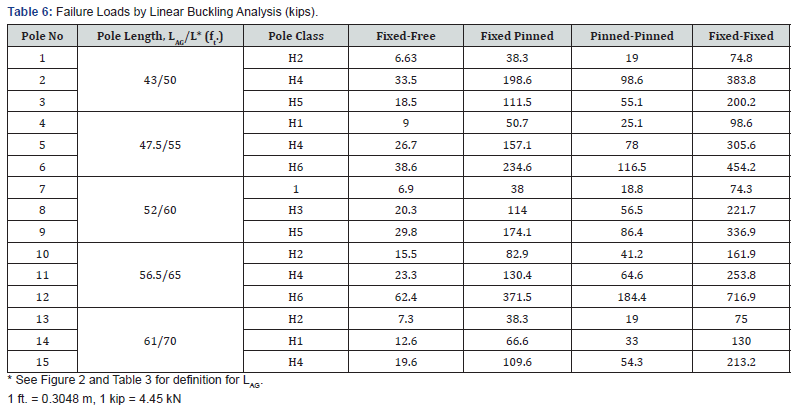
The adopted FE idealization is shown in Figure 3. To maintain consistency with the GCM, the effective length of the pole FE model is taken as the pole height above ground, LAG. Table 6 gives the critical buckling loads obtained by ANSYS for the 15 poles for various end conditions.

Comparison of Results and Discussion

The critical buckling loads from the Gere and Carter Method (Table 4) and FE linear buckling analysis (Table 6) are compared and the computed percentage discrepancy is shown in Table 7. There is reasonable agreement between the two sets of values, although the differences ranged from 12% to 24%. The values from GCM are consistently higher than the FE values. From Table 7, it is observed that the discrepancy is minimum (12.12%) in the pinned-pinned case and maximum (24.26%) for the fixedfree case. The average % discrepancy values for the four boundary conditions investigated were - 21.02, - 19.86, - 16.48 and - 17.23, respectively.

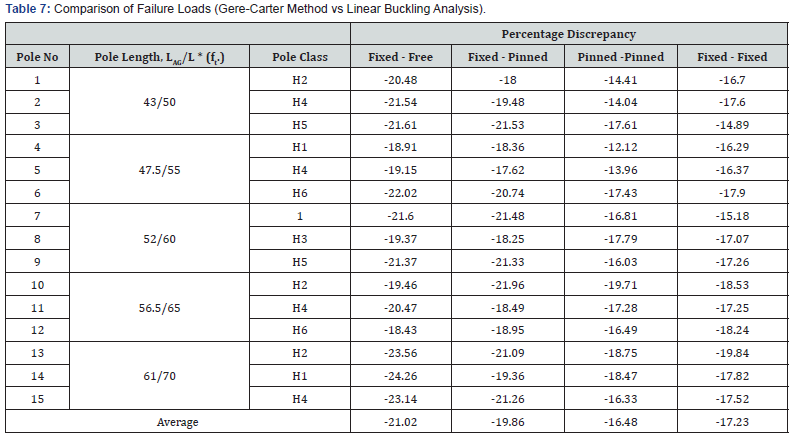
The main inferences that can be drawn – pending validation with full-scale testing – are that:

1. Using average values of modulus of elasticity E and tube thickness t may be one of the factors that affected the buckling capacities.

2. Accurate FE modelling for modular composite poles (RS Poles) may require an explicit consideration of each module with its specific geometric and material properties. This aspect may be considered for future analytical activities for such poles.

3. In the absence of other means of computing theoretical buckling capacities, the Gere and Carter Method may continue to be used for calculating nominal buckling loads, subject to a cautious understanding of its limitations and the application of a proper factor of safety

4. Only laboratory testing will help establish what rational factors of safety are needed for various loading situations.

Peabody and Wekezer [15] obtained somewhat different results for their FE analysis of an 80 ft. (24.4 m) - long wood pole where they compared FE results with those of Gere and Carter. The % discrepancy values for the same four boundary conditions were +4.43, - 1.74, - 0.35 and + 0.36, respectively. The paper recommended GCM for calculating buckling strength of transmission and distribution poles; but suggested performing a series of fullscale tests to validate GCM.

Upper and Lower Bounds of Buckling Capacities

As stated earlier, it is generally believed that the overall effective boundary conditions for a guyed pole may be between the fixed-free (k = 2) and fixed-pinned (k = 0.7). Therefore, these two situations may be treated as lower and lower bounds related to the buckling capacity. It is possible to obtain a value in-between the two bounds as a design reference. With a relevant factor of safety, this design value may be used as an allowable buckling capacity. Better estimates of the upper and lower bounds can be obtained by modelling the modular poles with their individual segments explicitly instead of adopting mean values.

Conclusion

Fifteen FRP composite poles were analyzed by a 12-element advanced FE model to determine critical buckling loads which were compared with theoretical estimates using the well-known Gere and Carter Method. The results from the two methods differed by about 12% to 24% attributed to the possible effect of using an average E and t in computations. The percentage of discrepancy between the buckling loads given by GCM and FEM is minimum for pinned-pinned end condition and maximum for fixed-free end condition. For all the cases studied in this paper, the maximum % discrepancy is about 24.26. For the cases considered it is seen that the Gere and Carter Method gives buckling loads that are different from those given by FEM.

Pending validation with full-scale testing, here are the main observations from the study:

1. Usage of average values of E and t may not be correct for modular composite poles.

2. Accurate FE modelling for modular poles requires an explicit consideration of each module with its individual geometric and material properties.

3. In the absence of other means for estimating theoretical buckling capacities, the Gere and Carter Method may continue to be used for calculating nominal buckling loads, subject to a cautious understanding of its limitations and the application of a proper factor of safety.

4. Only laboratory testing will help establish what rational factors of safety are needed for various loading situations.

To assist in routine design, the upper and lower bounds - and their mean value - of the buckling load can be considered. Given the uncertainty associated with correctly modelling the end restraints of a guyed pole, and the effects of averaging the modulus of elasticity and tube thickness, it is suggested that a series of full-scale tests be performed to rationalize on the findings of this and previous studies. Future analytical activities for assembled modular poles must include modelling each module as given with their specific properties.

References

1. Kalaga S, Yenumula P (2016) Design of Electrical Transmission Lines: Structures and Foundations, CRC Press.
2. (2015) Bulletin 1724E-200, Design Manual for High Voltage Transmission Lines, Rural Utilities Services. United States Department of Agriculture (USDA).
3. NESC-2017, National Electrical Safety Code, ANSI C-2, Institute of Electrical and Electronics Engineers, New York, USA.
4. Ali R (1970) Derivation of Stiffness Matrix for a Tapered Beam Element Report. Department of Transport Technology, Loughborough University of Technology, UK.
5. Aristizabal-Ochoa JD (1987), Tapered Beam and Column Elements in Unbraced Frame Structures. Journal of Computing in Civil Engineering 1(1): 35-49.
6. Ashraf M, Ahmad HM, Siddiqi ZA (2005) A Study of Power Transmission Poles. Asian Journal of Civil Engineering 6(6): 511-532.
7. Banerjee JR, Williams FW (1986) Exact Bernoulli-Euler Static Stiffness Matrix for a Range of Tapered Beam-Columns. International Journal for Numerical Methods in Engineering 23:1615-1628.
8. Chugh AK, Biggers SB (1976) Stiffness Matrix for a Non-Prismatic Beam-Column Element. International Journal for Numerical Methods in Engineering 10: 1125-1142
9. Costello GA (1967) Stability of Transmission Line Structures Journal of the Engineering Mechanics Division, ASCE 93:19-29.
10. Li GQ, Li JL (2007), Elastic Stiffness Equation for Tapered Beam Element. Advanced Analysis and Design of Steel Frames, Wiley Inter Science.
11. Sapalas V, Samofalov M, Saraskinas V (2005) FEM Stability Analysis of Tapered Beam-Columns, Journal of Civil Engineering and Management 11(3): 211-216.
12. Desai N, Yuan R (2006) Investigation of Bending/Buckling Characteristics for FRP Composite Poles, Proceedings, Earth and Space Conference, Houston, Texas.
13. Jung J, Abolmali A, Choi Y (2006) Finite Element Analysis of Tapered Steel and Fiber-Reinforced Plastic Bridge Camera Poles, ASCE Journal of Bridge Engineering 11(5): 611-617.
14. Gere JM, Carter WO (1962) Critical Buckling Loads for Tapered Columns. ASCE Journal of the Structural Division 88: 1-12.
15. Peabody AB, Wekezer JW (1994) Buckling Strength of Wood Power Poles Using Finite Elements. ASCE Journal of Structural Engineering 120(6):1893-1908.
16. (1997) ASCE 91, Design of Guyed Electrical Transmission Structures. ASCE Manual, Reston, Virginia, USA.
17. (2016). Composite Utility Poles- Electrical Transmission and Distribution Creative Pultrusions, Alum Bank, Pennsylvania, USA.
18. (2008) Standard Modular Composite Utility Poles, RS Poles, RS Technologies. Calgary, Alberta, Canada.
19. ANSYS (2015) Users Manual. Ansys Inc Canonsburg Pennsylvania USA.
20. (2003) Bulletin 1724E-153, Electric Distribution Line Guys and Anchors, Rural Utilities Services. United States Department of Agriculture (USDA).
21. (2007) IEEE-751, Trial Use Design Guide for Wood Transmission Structures. Institute of Electrical and Electronics Engineers, New York, USA.
22. (2012) PLS-POLE TM, Computer Program for the Analysis and Design of Transmission Poles. Power Line Systems, Inc Madison, Wisconsin, USA.