Analysis and Prediction of Uneven Settlement due to a Curved Shield Metro Tunnel
Hao Feng*
Shanghai Civil Engineering Co., Ltd. of CREC, China
Submission: February 05, 2019;Published: March 22, 2019
*Corresponding Author: Hao Feng, Shanghai Civil Engineering Co., Ltd. of CREC, China
How to cite this article: Hao Feng, Analysis and Prediction of Uneven Settlement due to a Curved Shield Metro Tunnel. Civil Eng Res J. 2019; 7(4):555720. DOI: 10.19080/CERJ.2019.07.555720
Abstract
Surface settlement is a natural phenomenon of ground disturbance in subway tunnel construction. Dissymmetrical surface settlement profiles are observed when shielding in a curved tunnel, but these observations are quite different from the predictions of typical formulae which indicate a symmetrical surface settlement profile in straight tunnels. Based on the field measurements from shielding subway tunnels in soft ground located in Southeast Asia, the relation of the uneven distribution of jacking thrust and the mechanics of dissymmetrical settlement are discussed, and the method of calculating the dissymmetrical settlement profile is proposed in this study. The methods proposed in this article can be used to properly predict the surface settlement induced by a single curved tunnel in similar geological and construction conditions. The results also provide a reference set of shield construction parameters.
Keywords: Curved Tunnel; Uneven settlement; Construction; Mass Rapid Transit
Introduction
The prediction and calculation methods of surface settlement have been extensively studied over the years. Peck and Schmidt (1969) first proposed the empirical formula using the Gaussian function to predict surface settlement:
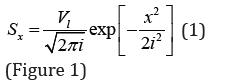
(Figure 1)
where Sx is the ground settlement at position x; x is the horizontal distance from the tunnel centerline to position x; Vl is the volume of ground loss; and i is the horizontal distance from the tunnel centerline to the inflection point of the internal half settlement curve.
Many scholars have revised Peck’s empirical formula to expand its practical applications. In addition to the empirical formula for calculating the surface settlement, the stochastic medium theory method is considered to be an effective method for accurately predicting the surface movement and deformation caused by underground mining [1]. In addition, the ground subsidence field measurement method and the laboratory test method have been widely used [2]. With the development of computing ability, numerical simulation has been widely used to study the stratum disturbance of soft soil caused by the shield excavation of a tunnel and the curved segment of a tunnel. However, there is no settlement calculation method for curved tunnels in the literature. Based on field measurements from shielding subway tunnels located in Southeast Asia, using regression modeling of measured data and mathematical simulation, the relationship between the uneven distribution of jacking thrust and the mechanics of dissymmetrical settlement are discussed, and a method of calculating the dissymmetrical settlement profile is proposed.
Predicting Surface Settlement Induced by Excavation of a Curved Tunnel
Surface settlement induced by curved tunneling
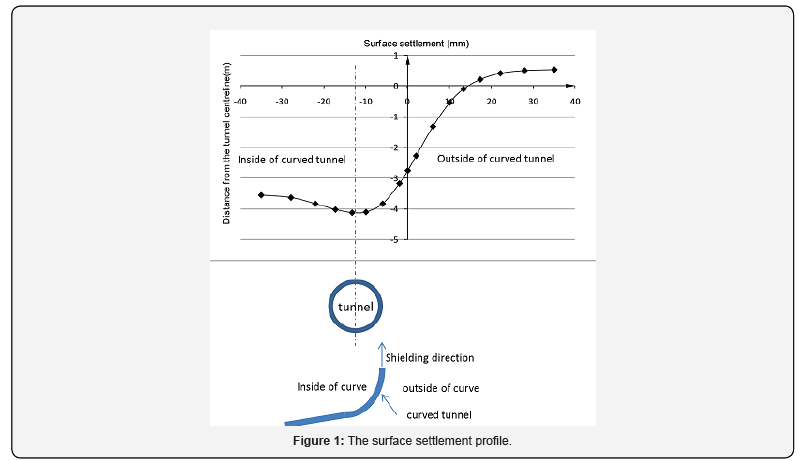
Meng [3] numerically simulated the ground settlement over a shield tunnel with an alignment radius of 450m at a depth of 16m using ANSYS software. The surface settlement profile was represented in his paper, as shown in Figure 1. The surface settlement profile in Figure 1 is not as symmetric as a Gaussian curve. The maximum settlement occurs near the tunnel longitudinal axis, slightly forward to the inside of the curve. Ground upheaval takes place on the outside of the curve, while this does not happen on the inside of the curve. Ground on the inside of the curve subsides more than that on the outside when comparing points along the cross section that are equal distances from the tunnel centerline. This indicates that the half settlement trough on the inside of the curve will be wider than its equivalent on the outside.
Formulation of predicting surface settlement induced by curved tunneling
From the numerical results of Meng [3], it can be inferred that function is not suitable for predicting the ground settlement induced by curved tunneling [4]. Therefore, it is reasonable to modify function by considering the alignment radius to get a better prediction of the settlement induced by curved tunneling [4]. To predict the surface settlement at the excavation face, the following assumptions can be made:
A. The maximum settlement occurs above the axis of tunnel, and
B. The surface settlement curve can be treated as two half settlement curves along the sides of the tunnel’s longitudinal axis, both of which can be represented by Gaussian functions with different coefficients.
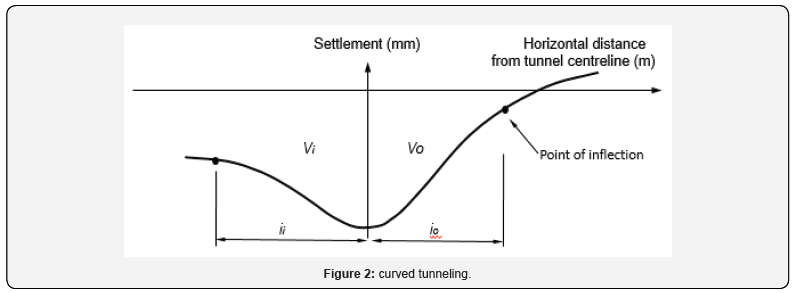
Based on these assumptions, the surface settlement trough induced by curved tunneling can be depicted as Figure 2. The formulation for calculating curved tunneling induced ground settlement would be expressed as follows:
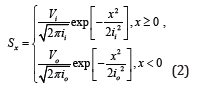
where x is the horizontal distance from the tunnel centerline; Vi and Vo are the volume of ground loss on the inside and outside of a curved tunnel; and ii and io are the horizontal distance from the tunnel centerline to the inflection point of the half settlement curve on the inside and outside, respectively.
Demonstration of Proposed Formulation
In order to demonstrate the formulation of curved tunneling induced settlement prediction, expressed as Equation (1), the first phase Mass Rapid Transit (MRT) project in Kuala Lumpur, which has several curved portions with different alignment radii, was chosen to validate the proposed method.
Project profile
The first phase MRT project in Kuala Lumpur consists of shielding construction. The tunnel runs from Semantan north portal through KL sentral to Parsa seni. The 2,716m long tunnel was built by an earth pressure balanced tunnel boring machine. It is buried at a depth of 13.2m. The shield machine with an articulation device has an outer diameter of 6,630mm. The lining ring is 5.8m in inner diameter, 275mm in thickness, and 1.4m in width. The hydraulic jacks of the shield are divided into four groups: the upper, lower, external, and internal groups. The average drilling speed of the shield machine was 6 rings per day.
Engineering geological condition
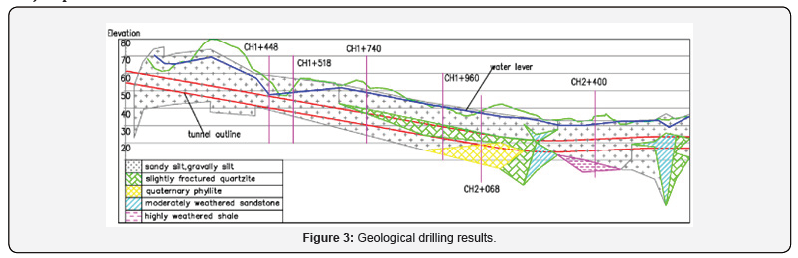
As indicated by the geological drilling results shown in Figure 3, the tunnel is mainly located in the Kenny Hill residual soil. The weathered Kenny Hill is approximately class IV with its joints fully developed. It is of complicated and diversified geological structure with mixed soft and hard stratum, containing many mixtures of soil and rock or interlayers of soil and gravel layers. There is highly weathered quartz rock, phyllite, mudstone, etc. The underground water level is 2.62 to 24.77m above the tunnel crown. The permeability coefficient of the formation is about 1.0 × 10−6 to 5.0 × 10−5m/s. The earth pressure balanced tunnel boring machine passes through mainly sandy silt and gravelly silt. The geological condition of each observation surface is shown Table 1.
Measurement of ground settlement
Plan of measurement: Several settlement observation sections had been arranged along the tunnel alignment. Ground settlement markers were installed along the observation sections. The ground settlement was measured from 10 days before the shield cutter reached the observation section to 30 days after the shield’s tail passed through the observation sections. The measurement was conducted at least once a day.

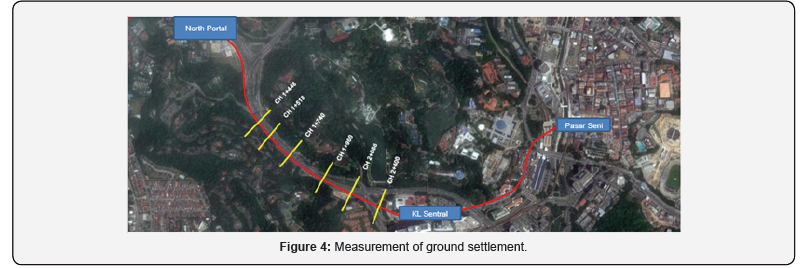
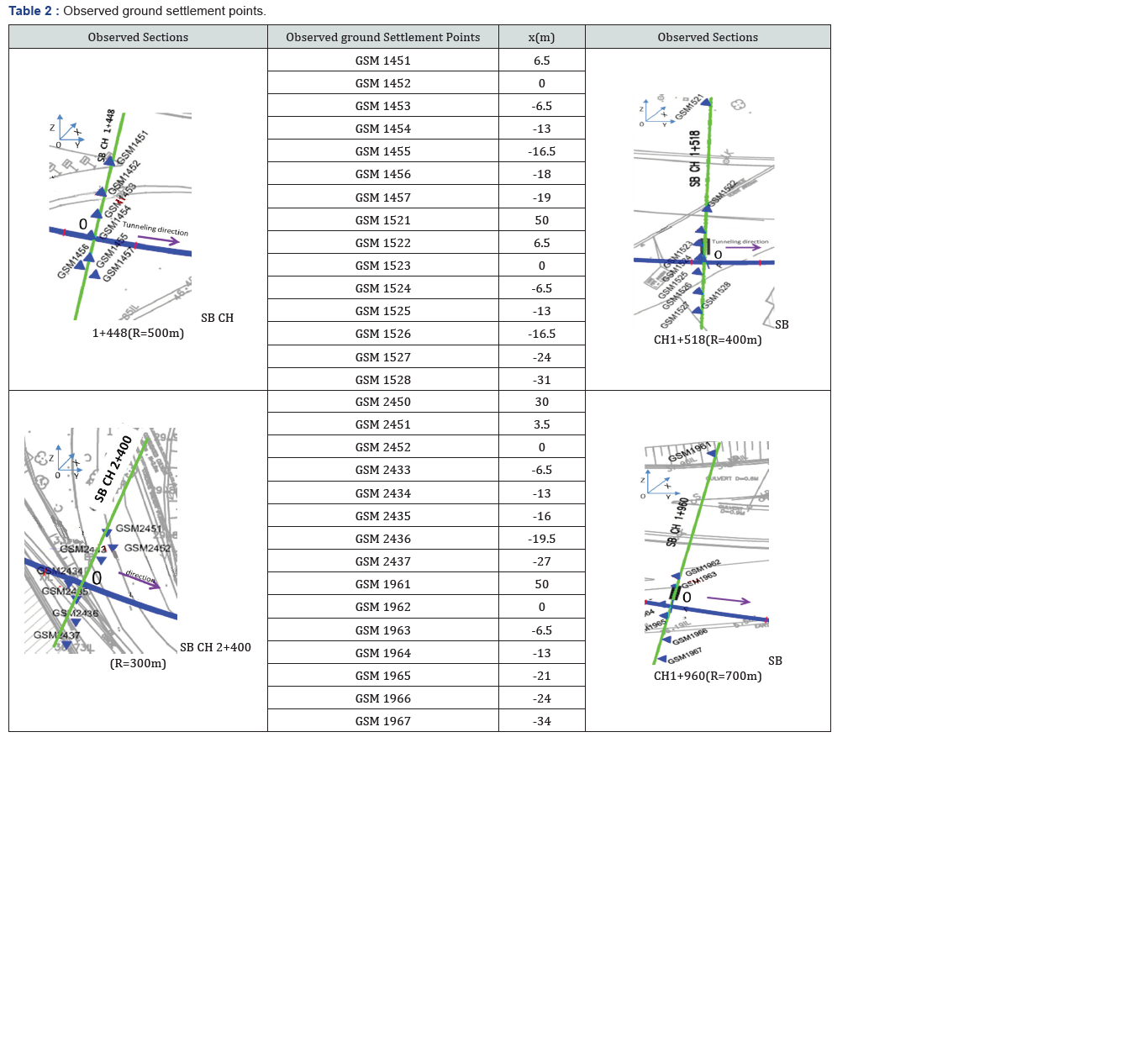
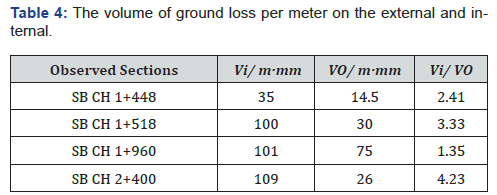
As shown in Figure 4, four representative observation sections in the curved portion were adopted in this paper. The chainage of the four observation sections are SB CH 1+448, SB CH 1+518, SB CH 1+960, and SB CH 2+400, the alignment radii of which are 500m, 400m, 700m, and 300m, respectively.
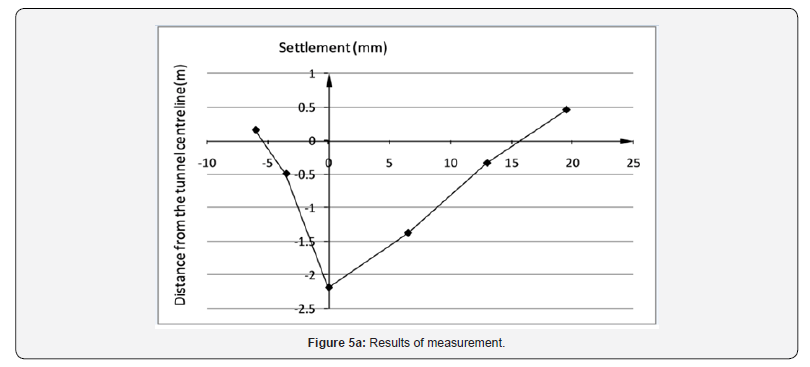
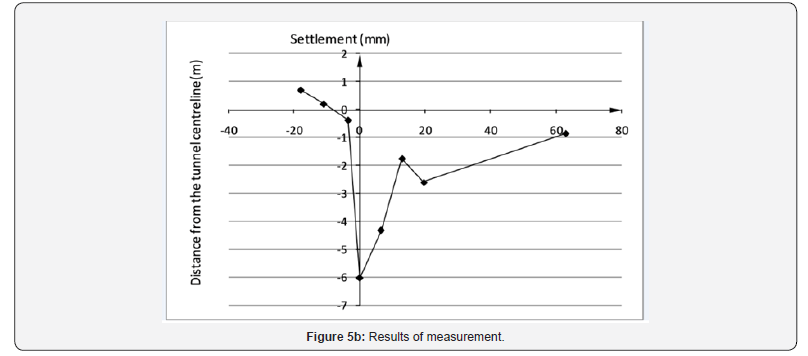
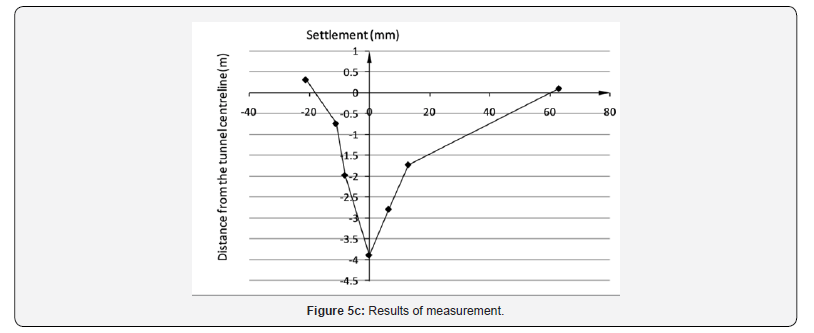
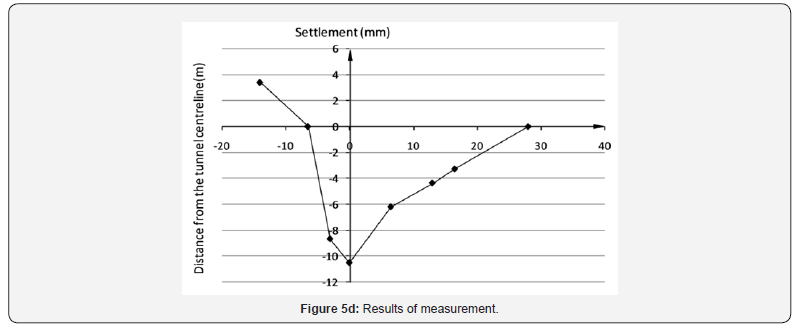
Results of measurement: The settlement measurements on the arrival of the cutter of the shield machine have been collected. The observed ground settlement points are shown in Table 2. The observed surface settlement curves at all the observation sections are plotted in Figure 5. In Figure 5, the x value is the horizontal distance from the centerline of the tunnel, and a positive x value indicates the internal of curved alignment; the z value is the ground settlement. Surface upheaval occurs much more frequently on the external of curved alignment than on the internal of curved alignment. The subsided ground on the internal of curved alignment outranges that on the internal. As shown in Figure 5a, the width of subsided ground on the internal of curved alignment is about 17.0m, which is much larger than around 6.5m on the external of curved alignment Figure 5bc. It can be inferred from Figure 5 that the maximum surface settlement always occurs over the centerline of the north tunnel. On average, the maximum settlement tends to grow as the radius of alignment decreases. Furthermore, the settlement on the internal of curved alignment is often larger than that on the external when comparing points with the same distance from the centerline. The ground settlement at x = 6.5m is −6.19mm, which is much larger than 0 mm at x = −6.5 m (see Figure 5d).
Jacking thrust: The jacking thrust of the shield is equipped with 22 cylinders, which are divided into groups A, B, C, and D. Groups A and C are distributed symmetrically on the left and right sides of the shield as shown in Figure 6.

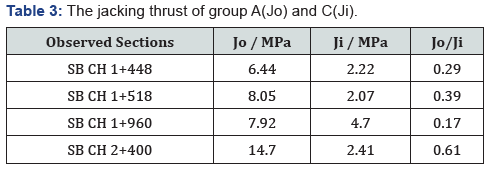
It was observed that the jacking force of group A on the outside of the curve was greater than that of group C on the inside of the curve when the earth pressure balanced tunnel boring machine reached the observation sections. During the research, the jacking force of the earth pressure balanced tunnel boring machine was recorded. The jacking forces Jo and Ji and their ratio (Jo/ Ji) for jacking groups A and C are shown in Table 3.
Analysis of the measurements
Regression fitting calculation: The observed surface settlements presented in Figure 5 are fitted by Equation (2), as shown in Figure 7. The fitted curve is highly consistent with the in-situ data, and the goodness of fit with the observed surface settlements points in-situ is 0.99, 0.96, 0.97, and 0.99, indicating that Equation (2) is applicable for this project.
Relationship between surface settlement and jacking thrust: As the radius of curved alignment varies, both the area and the shape of the surface settlement trough, as well as the uneven jacking thrust of the shield machine, will change accordingly. The variables for ground loss volume per meter Vi and VO were mathematically integrated with Origin software on both halves of the fitted settlement curves in Figure 8. Then, the volume of ground loss per meter on the outside and inside of the curved alignment, Vi and VO, are correspondingly obtained (Table 4). The relationship between Vi /VO and Jo/Ji is fitted by Equation (3), as shown in Figure 8.
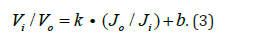


As a result, with the total ground loss volume Vl and the jacking forces Jo/Ji in-situ, we can obtain the ground loss volume Vi and VO through Equations (3) and (4), and then predict surface settlement Sx using formula (2) [5-18].
Conclusion
The following conclusions were drawn based on the measured settlements:
The prediction method of the surface settlement above the curved portion of a single shield tunnel was obtained and expressed as the following formula:
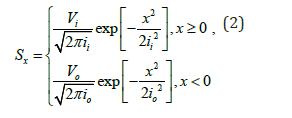
The relationship between uneven surface settlement and jacking force in this project was obtained (radius of curved alignment is more than 300m in this case) and expressed as the following equation:
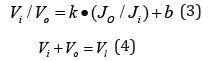
The ratios of Vi /VO and Jo/Ji have a positive relationship.
It was demonstrated that curved tunnel settlement can be described with the Formula and Equation in conclusions (1) and (2), and thus surface settlement can be calculated.
The settlement prediction formula in this paper is mainly given for the specific geological condition, which is Kenny Hill residual soil, at an alignment radius of more than 300m. Theoretically, extensive research should be conducted under other geological conditions, alignment radii, and construction conditions to further test the applicability of the proposed formulae.
References
- Shi CG (2003) Prediction of vertical strata movement and deformation of tunnel under shield construction. Rock and Soil Mechanics 1(25): 585-589.
- Chambon P, Corte J (1994) Shallow tunnel sincohesionless soil stablity of tunnel face. Journal of Geotechnical Engineering 120(7): 1148-1165.
- Meng XL (2011) Study on impact of big gradient and curve in small radius on the stability of shield tunneling excavation face and the stress of segment. Beijing Jiaotong University, China.
- Peck RB (1969) Deep excavations and tunneling in soft ground. In Proceedings of the 7th International Conference on Soil, Mechanics and Foundation Engineering, Mexico, pp. 225-290.
- Attewell PB, Woodman JP (1982) Predicting the dynamics of ground settlement and its derivatives caused by tunneling in soil. Ground Engineering 15 (8): 13-20.
- Fahimifar A, Ghadami H, Ahmadvand M (2014) The Influence of Seepage and Gravitational Loads on Elastoplastic Solution of Circular Tunnels. Scientia Iranica 21(6): 1821-1832.
- Ngoc-Anh D, Dias D, Oreste P (2014) Three-dimensional numerical simulation of mechanized twin stacked tunnels in soft ground. Journal of Zhejiang University-SCIENCE A 15(11): 896-913.
- Farrell R, Mair R, Sciotti A, Pigorini A (2014) Building Response to tunnelling. Soils and Foundations 54(3): 269-279.
- Faramarz M, Ali AR, Qasem BC, Erfan RD (2018) Application of petrographic image analysis in assessment of chemical attack in the concrete segments of a tunnel Articles in Press. Scientia Iranica, Iran.
- Goh KH, Mair RJ (2014) Response of framed buildings to excavation-induce d movements. Soils and Foundations 54(3): 250-268.
- Giardina G, DeJong MJ, Mair RJ (2014) Important aspects when modelling the interaction between surface structures and tunneling in sand. In: Yoo (Eds), Geotechnical aspects of underground construction in soft ground. Korean geotechnical society. Seoul, Korea: Taylor and Francis, University of bath, UK, pp. 263-268.
- Giardina GM, Hendriks AN, Jan GR (2015) Sensitivity study on tunnelling induced damage to a masonry facade. Engineering Structures 89: 111-129.
- Kasper T, Meschk G (2006) On the influence of face pressure, grouting pressure and TBM design in soft ground tunnelling. Tunnelling and Underground space Technology 21(5): 160-171.
- Oliaei M, Manafi E (2015) Static analysis of interaction between twin-tunnels using Discrete Element Method (DEM). Scientia Iranica 22(6): 1964-1971.
- Shen SL, Wu HN, Cui YJ (2014) Long-term settlement behavior of metro tunnels in the soft deposits of Shanghai. Tunneling and Underground Space Technology 40: 309-323.
- Verruijt A, Booker JR (1998) Surface settlements due to deformation of a tunnel in an elastic half plane. Geotechnique 46(4): 709-713.
- Oliaei M, Manafi E (2015) Static analysis of interaction between twin-tunnels using Discrete Element Method (DEM). Scientia Iranica 22(6): 1964-1971.
- Wang XD, Liu ZM, Ma JM (2015) Statistical evaluation of buildings disturbed from metro shield tunneling in soft soil. Proc. ITA WTC 2015 Congress, Dubrovnik, Croatia.






























