Prediction of Compressive Strength of Recycled Aggregate Concrete using LASSO
Arif Cekic1*, and Jale Tezcan3
1Intertek-PSI, Farmington Hills, USA
2Department of Civil and Environmental Engineering, Southern Illinois University,
Submission: March 13, 2018; Published: May 18, 2018
*Corresponding author: Arif Cekic, Intertek-PSI, 37483 Interchange Drive, Farmington Hills, Michigan, USA. Tel: 734-564-3562; Email: arif.cekic@psiusa.com
How to cite this article: Arif C, Jale T. Prediction of Compressive Strength of Recycled Aggregate Concrete using LASSO. Civil Eng Res J. 2018; 5(1): 555654. DOI: 10.19080/CERJ.2018.05.555654
Abstract
The past few decades have seen a continued interest in the use of industrial waste and byproducts in the production of Portland cement concrete due to increasing landfill costs, concerns on the carbon footprint of the construction industry, and the need to preserve natural resources. While the recent increase in the use of recycled concrete aggregate in the construction industry has made the engineering properties of recycled aggregate concrete a research priority, research efforts have focused mainly on the effect of mix ingredients and concrete maturity on the strength and stiffness properties of concrete. The effect of elevated temperatures has not been investigated. Motivated by the fact that a variety of structures are exposed to elevated temperatures during their service life, this paper investigates the compressive strength of recycled aggregate concrete subjected to elevated temperatures. Using experimental data with 31 test results, the relative importance of four variables, namely, temperature, water-to-cement ratio, recycled aggregate replacement ratio and concrete maturity beyond 28-days, was ranked. Analysis results indicate that the water-to-cement ratio is the strongest predictor of the compressive strength, followed by temperature, replacement ratio, and concrete maturity in that order. The method described in this paper can be applied to a variety of modeling problems in environmental and sustainability research where the relative importance of a set of variables is to be investigated.
Keywords: Recycled aggregate concrete; Compressive strength; Water-to-cement ratio; Replacement ratio; Exposure temperatures; Regression; Lasso
Abbreviations: MSE: Mean Squared Error; DOF: Degrees of Freedom; MSE: Mean Squared Error; LASSO: Least Absolute Shrinkage and Selection Operator; ANN: Artificial Neural Network; SVM: Support Vector Machine; W/C: Water-to-Cement ratio; OLS: Ordinary Least Squares
Introduction
Industrial waste and byproducts have been utilized in the construction industry for decades due to economic and environmental considerations. Increasing landfill costs, concerns on the carbon footprint of the construction industry, and the need to preserve natural resources have motivated a continued interest in the use of industrial waste and byproducts in the production of Portland cement concrete [1]. Fly ash and silica fume [2], waste tire [3-5], waste glass [6,7], and waste plastic [8-10] have been used as a replacement for cement or aggregate in the concrete mix. The use of recycled concrete aggregate as a replacement for aggregate is becoming increasingly common in concrete production [11]. Recycled concrete aggregate, also referred to as recycled crushed concrete, is typically obtained through demolition of Portland cement concrete elements of buildings, roads, and other structures [12]. Typical applications of recycled aggregates include general bulk fill, base or fill in drainage projects, sub base or surface material in pavement and road construction, and new concrete production.
Many researchers [13-17] have focused their attention on engineering properties of Portland cement concrete made with recycled concrete aggregates. The main focus of many of these studies has been the evaluation of the appropriateness of recycled concrete aggregate as described in ASTM C33 [18], the standard specification for concrete aggregates. The mechanical properties of concretes made with recycled aggregates have been observed to be different from those made with natural aggregates. These differences were generally attributed to the mix ingredients and concrete maturity. The effect of elevated temperatures has not been investigated, despite the fact that a variety of non-building structures such as concrete chimneys, pressure furnaces, reactor vessels and coal gasification vessels are exposed to elevated tem-peratures during their operation, and others may be subjected to high temperatures due to a thermal shock or fire.
This study investigates the effect of four variables, namely temperature, water-to-cement ratio, recycled aggregate replacement ratio expressed as a percentage, and concrete maturity be-yond 28-days,on the compressive strength of recycled aggregate concrete. For this purpose, a predictive model has been constructed usinga dataset [19] with 31 test results containing recycled aggregates at various water-cement and replacement ratios, ex-posed to elevated temperatures up to 250 °C. Half of the specimens were tested at 28 days, and the rest at 90 days. The effect of four variables on the compressive strength has been investigated, and their relative importance has been ranked using Least Absolute Shrinkage and Selection Operator (LASSO), which can be described as a penalized regression technique with a built-in capability of variable selection.
While the focus of this study is limited to the compressive strength of recycled aggregate concrete, the method used in this study is applicable to a variety of problems in environmental and sustainability research where data-driven approaches are utilized. The LASSO method described in this paper not only facilitates identification of the important factors affecting a quantity of interest, but also allows construction of predictive models with reduced susceptibility to over fitting. Because the risk of over fitting increases as the ratio of the number of predictors to the number of observations increases, selection of a compact set of variables is important in cases where a small number of observa-tions are available, such as this study. Furthermore, identification of a compact set of relevant variables makes the model easier to interpret, which in turn can help corporations and government organizations make deliberate decisions when evaluating and comparing alternative solutions to environmental and sustain-ability problems.
The remainder of this paper is organized as follows. Section 2 provides a brief overview of the techniques that have been used in predictive modelling of concrete properties and argues that such techniques are not ideal for the current study, which is based on only 31 test results. Section 3 presents a mathematical description of the Least Absolute Shrinkage and Selection Operator (LASSO). Section 4 is devoted to the investigation of the relative importance of the four variables on the compressive strength, and comparison of the output of regression models with increasing levels of com-plexity. Section 5presents a discussion of the bias-variance tradeoff in the context of model selection. Finally, Section 6 concludes the paper by presenting a brief summary of this study.
Regression Techniques for Predicting Concrete Properties
Many recent research efforts have been focused on the understanding of how different mix ingredients affect various properties of fresh or hardened concrete. A variety of regression models have been constructed in an effort to understand the influence of various mix ingredients on the properties of the concrete, and to predict the property of interest for a specified mix design.
Various recent studies [13-17,20-26] have used black box approaches such as the Artificial Neural Network (ANN) and Sup-port Vector Machine (SVM), to model concrete properties such as compressive strength and elastic modulus. These approaches have been found to yield satisfactory results, offering better predictive ability than the Multiple Linear Regression.
Black box approaches are not suitable in this study for two reasons: First, due to the scarcity of experimental data on recycled aggregate concrete exposed to elevated temperatures, this study is based on a dataset of only 31 observations. Black-box approaches learn the input-output relationship from the training data, without a specified parametric model. When a dataset with a large number of observations is available, an accurate model can be obtained using ANNs and SVMs as long as the complexity of the model is controlled. With a small dataset, model over fitting is an important concern. Reserving a portion of the available data as a test set, as commonly done in black box modeling, would further reduce the size of the data to be used in constructing the model. Second, black box approaches produce a model which is difficult, if not impossible to interpret. Our goal in this paper is to rank the importance of the four variables in regards to the compressive strength of recycled aggregate concrete.
In this paper, we use the Least Absolute Shrinkage and Selection Operator (LASSO) to evaluate the importance of the four variables. Being a penalized regression approach, the LASSO reduces the risk of over fitting. The LASSO is suitable when the number of available observations is low relative to the number of predictors. The LASSO model is described in Section 3.
The Least Absolute Shrinkage and Selection Operator
This section describes the mathematical background of the Least Absolute Shrinkage and Selection Operator (LASSO), pro-posed by Tibshirani [27]. In the discussion below, bold letters are used to denote vectors and matrices.
Consider a dataset containing n independent observations (x(,),y(i)) i = 1,2,...n , x(i) = [xf0,where is the lx p vector of input variables of the ith observation and y(') is the corresponding scalar output. It is assumed that the input x(i) and the output yare related through the linear equation

where μ is the p xl coefficient vector and e(i> is the random error term associated with y(i). The error term is assumed to have mean zero and variance a2. Equation (1) can be written in matrix form as
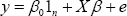
Where y is the n x l output vector, (0 is the intercept term, 1n is the n xl vector of ones, X is the n x p input matrix containing x{‘) as its ith row and isthe n x 1 vector of independent and identically distributed random errors. Assuming that each column of X is shifted and scaled to have zero mean and unit variance, the expected value of y is equal to the intercept term Thus, the intercept term is predicted as 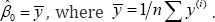 As a consequence, without loss of generality, it can be assumed that y = 0 effectively removing the intercept term from the model. This results in the model
As a consequence, without loss of generality, it can be assumed that y = 0 effectively removing the intercept term from the model. This results in the model
y = X + e
where y now measures the deviations from the mean of the observed output.
The ordinary least squares (OLS) estimate of the ( vector, which will be denoted as ( is obtained by minimizing the sum of the squared residuals. That is,
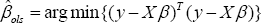
Under the Gauss-Markov assumptions, the OLS estimate is unbiased. Further, it has the smallest variance of all linear unbiased estimators. Because the accuracy of an estimator is measured by its mean squared error (MSE), which is equal to the sum of the variance of the estimator and its squared bias, (oS is the best linear unbiased estimator (BLUE) of the true parameter vector (. The variance of a biased estimator, however,can be much smaller than that of (, resulting in a smaller MSE.
Ridge regression, also known as the penalized least squares method, offers a technique for reducing the variance of the esti-mated regression coefficients. Ridge regression shrinks the coeffi-cients toward zero, making the estimate more stable than the OLS estimate. Ridge regression coefficients are determined by solving the following optimization problem:
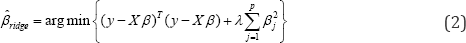
where λ< 0 is a user-selected parameter that controls the amount of shrinkage. The parameter X can be selected using cross validation.
A recently proposed biased estimator is the LASSO, which solves the following optimization problem
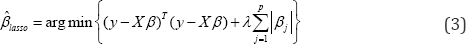
where λ< 0 is a user-selected parameter that controls the amount of shrinkage. The lasso parameter can be selected using cross validation, as described in Section 4.3. Similar to the ridge regression, the LASSO also prefers smaller coefficients, thus resulting in coefficient estimates that are more stable than the OLS method.
Although the LASSO problem given in Equation (3) is looks very similar to the ridge regression problem given in Equation (2), the solutions PIid!ee and (3laso exhibit significant differences. In the process of shrinking the coefficients, the LASSO sets some of the coefficients exactly to zero. This is unlike ridge regression, where the coefficients are shrunk but never set equal to zero. By setting some coefficients equal to zero and retaining the ones strongly affecting the output, the LASSO performs variable selection. Iden-tification of such variables can improve the interpretability of the resulting model, especially when there is a large number of pre-dictors.
LASSO model for predicting the compressive strength
This section presents the application of LASSO described in Section 3 for predicting the compressive strength of concrete. Fol-lowing a description of the dataset in Section 4.1, we describe the predictor and target variables and construct the LASSO model in Section 4.2, Section 4.3 describes the procedure used in selecting the shrinkage parameter of the model. Section 4.4 presents the results and discusses the relative importance of the predictors.
Data
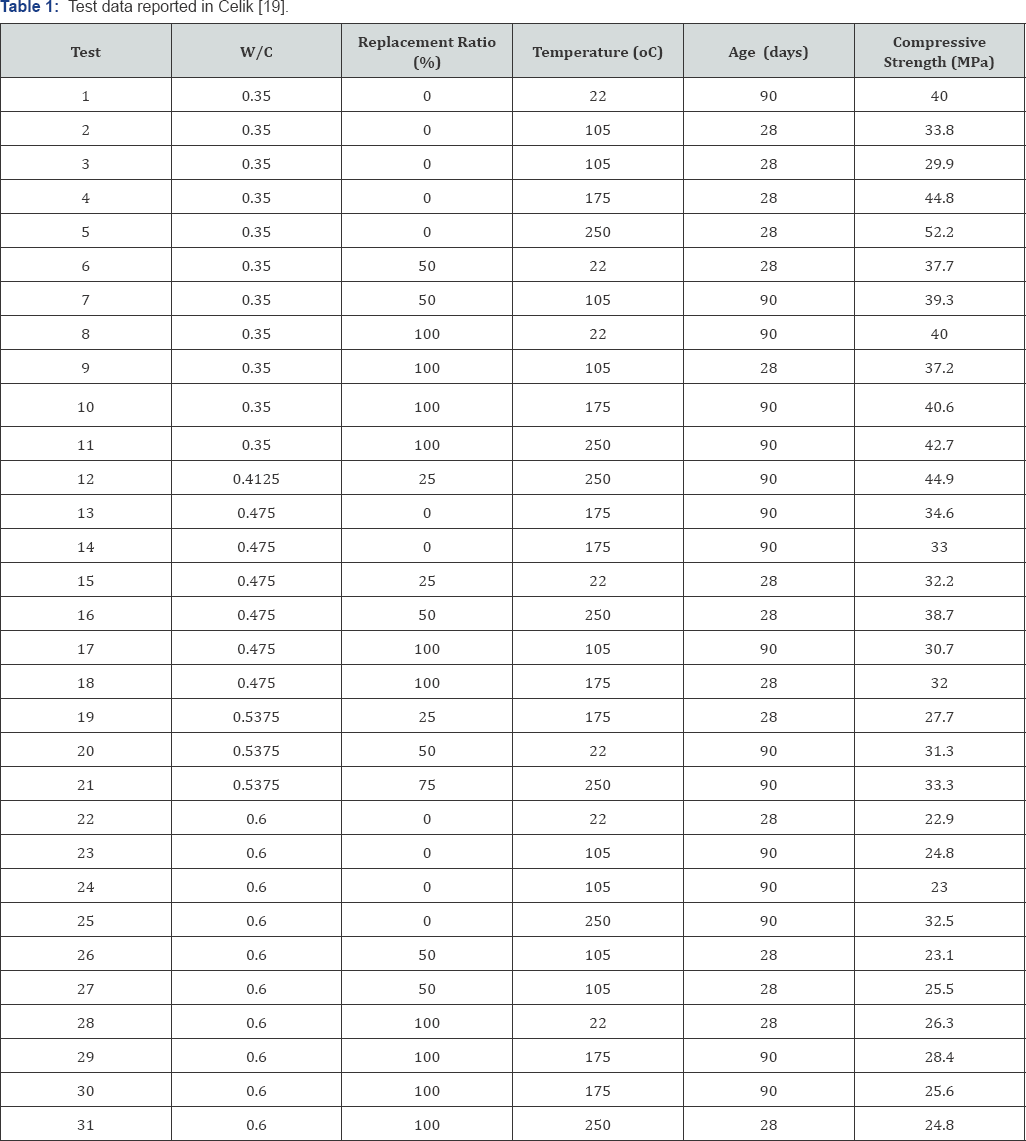
The dataset used in this paper is taken from Celik [19]. The datasetincludes results from 31 compressive strength measurements, where each measurement is obtained as the average of three specimens. The test data is reproduced is Table 1.
Input and Target Variables
The predictor set consists of four input variables: the wa- ter-to-cement ratio by weight (W/C), replacement ratio of the recycled aggregate, expressed as a weight percentage (RR), tem-perature in °c (T), and age in days (A). The target variable is the compressive strength of concrete in MPa (fc), obtained as the average of three specimens. Thus the output of the ith observation is y<0 = fCf ) and the corresponding input vector is x(i ) = [W/C(i \ RR(‘ \ T(i), A(i)]
Estimation of the LASSO parameter
The LASSO has a user-defined parameter X, which controls the degree of shrinking of the regression coefficients. Referring to Equation (3), note that X = 0 corresponds to the unpenalized, Ordinary Least Squares method, while X = œ corresponds to all coefficients in being equal to zero.
We select the LASSO parameter λ using five-fold cross-validation [28]. In 5-fold cross validation, the dataset is randomly partitioned into 5 subsets of approλimately equal size. The model for λ, a candidate value for is constructed using four of the subsets, and the prediction error is computed over the remaining subset, called the test set. The process is repeated 5 times, each time using one of the subsets as the test set, and average prediction error over the 5 repetitions is considered to be cross-validation error associated with λ*. Repeating this process over a grid of λ values, a plot of the average prediction errors and the standard errors is generated. The value λ can be selected by eλamining a plot of the cross validation errors versus λ The value minimizing the cross validation error, hereafter referred to as λmin can be selected. However, as observed by Breiman, Friedman [29], a model constructed using λmin is still susceptible to overfitting. Breiman, Friedman [29], define the one standard error rule (1SE rule) as using the simplest model whose error is no more than one standard error above the minimum. In the LASSO formulation, the 1SE rule suggest using the largest λ value for which the cross-validation error is at most one standard error above the minimum, hereafter referred to as λopt, instead of λmin.
Results
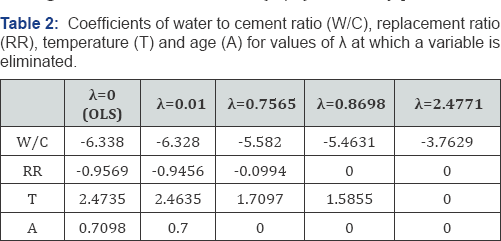

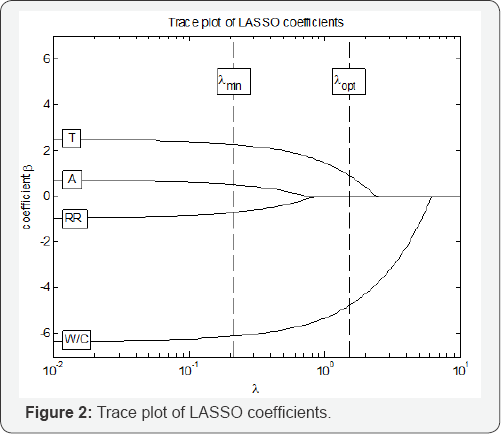
Referring to Figure 1, the 1 SE rule suggests selecting λoptopl = 1.3219 as the shrinkage parameter. This value of the shrinkage parameter corresponds to a model with two predictors: wa- ter-to-cement ratio and temperature. This can also be seen from Figure 2, which shows the coefficients of the four predictors versus the LASSO parameter λ
These results suggest that the four variables affecting the com-pressive strength of recycled aggregate concrete can be ranked in the order of decreasing importance as follows: (1) Water-to-ce- ment ratio, (2) Temperature, (3) Replacement ratio, and (4) Age. Note that in this study, the age variable only takes two values, 28 days and 90 days. Thus, the ranking of Age variable as the least important implies that little strength is gained after 28 days, as expected.
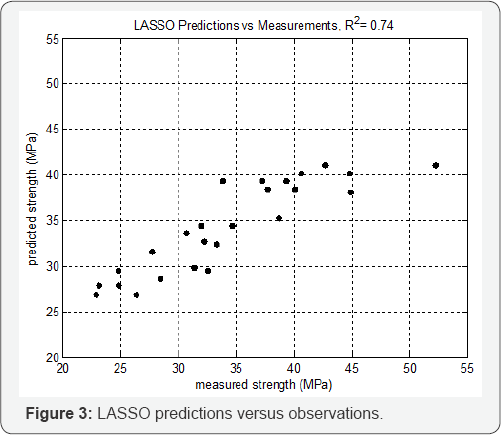
The LASSO model with the two selected variables (wa- ter-to-cement ratio and temperature) was used to obtain the predictions for the compressive strength. The predicted strength values versus the measured values are shown in Figure 3. The coefficient of multiple determination (R2) was computed as 0.74, indicating that the LASSO model is able to explain 74% of the observed variance in the compressive strength
Discussion
In this section, we provide a comparison of the OLS and LASSO approaches in terms of (1) their ability to explain the observed variance in the compressive strength, quantified by the coefficient of multiple determination, and (2) how well they can generalize to unseen data, based on theoretical understanding of the two methods.
To compare OLS and LASSO in terms of their ability to explain the observed variance in the compressive strength, we define four model types represented by the following parametric forms:
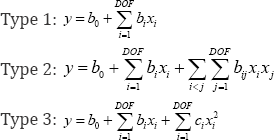
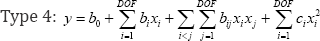
In the equations above, the parameters b0, b, bv and ci repre-sent the constant term, the coefficient of the linear term x , th coefficient representing the interaction between x and xj, and the coefficient of the squared term x], respectively. Note that all four model types defined above are linear in parameters even though three of the four models are nonlinear in variables. Because of the linearity in parameters, linear regression applies to all four model types.
For each model type described above, we perform regression using one, two, three, and four degrees of freedom (DOF), overall producing 16 OLS models and 16 LASSO models. The predictors corresponding to different degrees of freedom are shown in Table 3
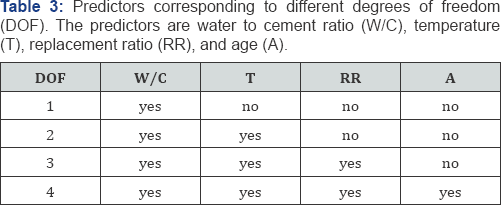
Table 4 & 5 show the coefficients of multiple determination ( R ) obtained using OLS and LASSO approaches. Note that as the OLS approach requires a preselected set of variables, variable selection has been performed using LASSO, regardless of the choice of the regression approach used in the final model.


Examination of the R2 values presented in Tables 4 & 5 leads to the following observations. First, as expected, the R2 values from the OLS approach (Table 4) increases as the number of predictors used in the model (DOF) increases. Second, the OLS approach produce higher R2 values as the complexity of the model's parametric form increases. In this paper, the Type specification is intended to represent this complexity, although the complexities of Type 2 (constant, linear and interaction terms) and Type 3 (constant, linear, and squared terms) are not directly comparable. This fact is reflected in Table 4, which shows an increase in R2 values between Types 2 and 3 for one and two degrees of freedom, and a decrease for three and four degrees of freedom.
The changes in the r2 values with increasing DOF and Type values is less predictable in the LASSO models, as Table 5 indicates. While the small size of the dataset and the lack of knowledge regarding the true parametric form of the relationship between the compressive strength and the four predictors make it difficult to interpret the r2 values as a reliable indicator of the model's accuracy, the lack of a strong trend in R2 values from the LASSO approach shows its lessened susceptibility to over fitting, compared to the OLS approach. Over fitting is an issue strongly linked to variance of a model, affecting the generalizability of the model to observations not included in the dataset.
In the context of bias-variance trade-off, the differences be-tween the OLS and LASSO approaches can be summarized as fol-lows. It is well known that the regression estimates from the OLS approach are unbiased. The LASSO approach introduces bias into the solution, which can lead to a considerable reduction in variance compared to the OLS solution. The reduction in variance, in turn, leads to a reduction in the Mean Squared Error (MSE), despite the increase in bias. As the MSE, which takes into account both the bias and the variance, is the most relevant quantity in model selection, the LASSO offers better generalization to the unseen data, compared to the OLS approach.
It should be emphasized that the bias-variance discussion presented above is based on the well-established theoretical un-derstanding of the two approaches. In practical applications, bias and variance of a model cannot be computed since the true con-ditional distribution of the output given the input is not known. Further, bias-variance decomposition, which relies on averaging over ensembles of datasets cannot be performed with a single ob-served data set.
Conclusion
In this paper, the compressive strength of recycled aggregate concrete subjected to elevated temperatures has been investigated through LASSO and OLS regression, using a dataset of 31 observations, containing four predictors: temperature, water-to- cement ratio, recycled aggregate replacement ratio and concrete maturity beyond 28-days. Using the Least Absolute Shrinkage and Selection Operator, the four variables were ranked in the order of decreasing relative importance as water-to-cement ratio, temperature, replacement ratio, and concrete maturity beyond 28-days.Regression models with four different parametric forms were constructed using one, two, three, and four best predictors, and the models' ability to explain the observed variance in the compressive strength were compared. The advantage of the LASSO approach in terms of the bias-variance trade-off was discussed in the context of model selection.






























