Vertical Flexibility in Isolation Systems
James M Kelly1* and Jiang Jun Lee2
1Earthquake Engineering Research Center, University of California, Berkeley, USA
2Department of Civil and Environmental Engineering, University of California, Berkeley, USA
Submission: December 03, 2017; Published: March 19, 2018
*Corresponding author: James M. Kelly, Professor Emeritus, Earthquake Engineering Research Center, University of California, Berkeley, USA, Email: jmkelly@berkeley.edu
How to cite this article: M K, Jiang J L. Vertical Flexibility in Isolation Systems. Civil Eng Res J. 2018; 4(1): 555629.DOI: 10.19080/CERJ.2018.04.555629
Abstract
This paper will review the history of three-dimensional (3-D) seismic isolation, its implementation and its drawbacks. It will cover the theoretical analysis of the rigid block on springs and the circumstances under which the various motions are and are not uncoupled. We will also review the records from a building with a 3-D isolation system that was impacted by fairly severe earthquake action. This review suggests that the search for full 3-D isolation is unlikely to be successful.
Introduction
While seismic isolation has been well accepted and widely used for over thirty years, it has been horizontal isolation that has predominated. The search for full 3-D seismic isolation has been the holy grail of research for all of these thirty years. It was originally assumed that they could be achieved by use of low shape factor elastomeric bearings that is bearings with thick rubber layers that provide a low vertical stiffness in concert with low horizontal stiffness. One of the earliest applications of low shape factor bearings was a research laboratory building constructed by the Kajima Construction company in 1987 as both a demonstration building and as a research facility [1]. The isolation system for the building was made up of eighteen laminated natural rubber bearings with a shape factor of 5.2 and several hysteretic (steel rod) dampers plus oil dampers. The design frequencies were 0.5Hz horizontally and 5Hz vertically The system was designed to provide 3-D seismic isolation and also since the building housed an acoustic laboratory, to filter out ground-borne vibrations, which it was shown to do very effectively. The bearings were supported on steel boxes to allow for adjustments for creep effects, which may be anticipated in low shape factor bearings using filled natural rubber.
An experimental research program on low shape factor natural rubber was carried out around the same time at the Earthquake Simulator Laboratory of University of California, Berkeley Earthquake Engineering Research Center (EERC). The purpose of this research program was to study the mechanical characteristics of low shape factor bearings intended to be for a then new type of liquid metal reactor named SAFR designed by Rockwell International. The reactor module was to be shop- fabricated and shipped to the site. Maximum horizontal and vertical accelerations of 0.3g were specified and to allow siting in highly seismic regions, it was decided to isolate the plant with a 3-D isolation system using low shape factor bearings in this case with a shape factor of 2.5. A very extensive test program on full size and scaled bearings was carried out for the SAFR program with results reported in EERC reports and papers (for example EERC 89/13) [2]. It was intended to use the large shaking table at the Earthquake Simulator Laboratory to study the dynamics of a model of the reactor building on these bearings but the SAFR program was shut down before that could be done.
Although the Kajima project and the SAFR test program seemed to be positive to the idea of using elastomeric bearings for 3-D isolation, further efforts involved other approaches such as steel springs and combined systems. The steel spring approach will be covered in detail in later sections. The combined systems have very sophisticated elements such as air springs developed by the Japanese nuclear industry. Because of their complications and expense, these systems have not been accepted for civil construction and the search for a practical and inexpensive system continues. In this paper we will explore the dynamics of the 3-D isolation system to highlight the dilemma faced by the designers of these systems and to look at how, at least in one system they respond to actual earthquake attack.
Isolation Systems with Vertical Flexibility
In most cases, isolation systems have only been considered for horizontal isolation that the vertical flexibility of the system is negligible. However, there are systems that can have a low vertical stiffness comparable to the horizontal stiffness. There are also situations where vertical isolation is considered to be essential. If the vertical input to be eliminated is ambient ground vibration, the natural rubber isolation system can provide this but if the vertical input is seismic, the situation becomes considerably more complicated. Nevertheless, rubber bearings and steel coil springs have been used in an attempt to provide both vertical and horizontal isolation in a single system. In an early example of a rubber isolation system to protect a structure from earthquakes was in 1969 for an elementary school in Skopje, Former Yugoslavia Republic of Macedonia. The Pestalozzi School, a 3-story concrete structure designed and built by Swiss engineers (Figure 1), is isolated by a system which was known at the time as the Swiss Full Base Isolation-3D (FBI-3D) System [3,4].


Unlike more recently developed rubber bearings, the rubber blocks used here (Figure 2) are completely unreinforced so that the weight of the building causes them to bulge sideways. Glass blocks (Figure 3) acting as seismic fuses are intended to break when the seismic loading exceeds a certain threshold. Because the vertical and horizontal stiffnesses of the system are about the same, the building will bounce and rock backwards and forwards in an earthquake but this was the intention of the inventor as implied by the name.
These bearings were designed when the technology for reinforcing rubber blocks with steel plates, as in bridge bearings was not highly developed nor widely known, and it is unlikely that this approach will be used again. It is worth noting that the original set of rubber bearings was replaced in 2008 by more conventional modern steel reinforced bearings under a contract from the NATO Science for Peace Program. The details of the program to produce and to replace the old isolators with the new isolators is provided in two publications [5,6].
The GERB system is based on steel springs with viscous dampers and is intended for simultaneous vertical and horizontal isolation. It was developed originally for the vibration isolation of power plant turbine generating equipment. It uses large helical steel springs that are flexible both horizontally and vertically. The vertical frequency may be around 3-5 times the horizontal frequency. The steel springs are completely without damping and the system is always used in conjunction with the GERB Viscodamper. As in all 3-D systems, there is very strong coupling between horizontal motion and rocking motion because the center of gravity of the isolated structure is above the center of stiffness of the isolation system. This type of system becomes practical as a seismic protection approach only in situations where the center of gravity and the center of stiffness are at the same level such as a reactor vessel in a nuclear power plant, for example.

The system has been tested on the shake table at Skopje, Macedonia [7], and has been implemented in Lowe Residences, two steel frame houses in Santa Monica, California (Figure 4). Each building is supported at its corners by GERB helical springs and viscous dashpots. A single spring damper unit at a corner of one of the buildings is shown in Figure 5. Additional springs are distributed around the building perimeters. These houses were strongly affected by the 1994 Northridge earthquake. Their response was monitored by strong motion instruments and the measured response, described in more detail later, revealed that the isolation system was not very effective in reducing the accelerations in these buildings most likely due to the rocking motion.

Dynamics of a Rigid Block on Springs
A rigid block of mass M and moment of inertia I is supported by two springs with stiffnesses k1x,k1z and k2x,k2zas shown in Figure 6.

The three equations of motion of the block in terms of relative displacements at the center of mass vx,vz and the rotation of the block θ are
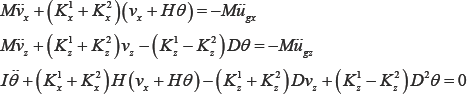
For an isolated system it is most likely that K = K2 and K1 = K2 from which we define the three overall stiffnesses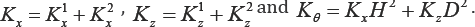
We now define the rotation as an equivalent displacement vθ = Hdand define the radius of inertia of the block R where I = MR2. The three nominal frequencies of the system are, 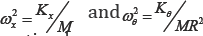 in terms of which the equations of
in terms of which the equations of
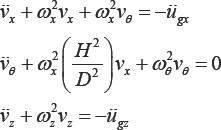
It is clear that in the case of a symmetric system the vertical motion is uncoupled from the other two and can be treated separately. The eigenvalues of the vector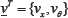 from the first two coupled equations denoted by
from the first two coupled equations denoted by 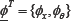 and given by
and given by 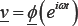 leads to eigenvalue frequencies w1andw2. The equations for the mode shapes corresponding to these frequencies are
leads to eigenvalue frequencies w1andw2. The equations for the mode shapes corresponding to these frequencies are

Substituting these values back into the equations for , gives the solution for ø1ø2 and f. gives the solution forø1and ø2 .To verify that these mode shapes satisfy the requirement of orthogonality, it is necessary to rewrite the reduced equations of motion in such a way that both the reduced mass matrix and the reduced stiffness matrix are symmetric, that is
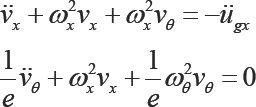
and in this case the reduced mass matrix 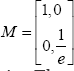 with the modes orthogonal with respect to this matrix. They can then be used as a basis for a dynamic analysis by expressing the displacement vector
with the modes orthogonal with respect to this matrix. They can then be used as a basis for a dynamic analysis by expressing the displacement vector 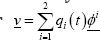 in terms of which the above equation becomes
in terms of which the above equation becomes

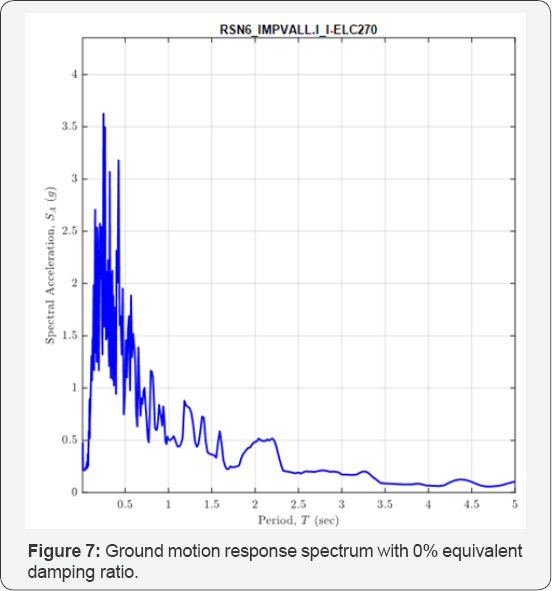
Thus showing the mode shapes are orthogonal and can be used as basis for dynamic calculations. For this example, we have M1 = 1.2251, M 2 = 5.441 and L = 0.8162, L2 = 0.1838. To determine the dynamic response it is necessary to define the uncoupled horizontal period which here we will take as one second. From this, the uncoupled horizontal frequency is rad/sec and the uncoupled rotational frequency is me=-/32;t rad/sec. The resulting periods of the coupled system are T = 1.545 sec and T2 0528 sec showing that the horizontal period is lengthened and the rocking period is reduced by the coupling between the two components. Taking as an example the Imperial Valley record from El Centro1940, the response spectrum of which is shown below in Figure 7, the estimates of the horizontal displacement and rotational displacement (the corner horizontal displacement in addition to the center of mass displacement) illustrate the fact that the rocking is a very large part of the movement of the structer in the case.
The spectral acceleration values at the first and second mode periods are SA (T1 = 1.545) = 0.3403g and sa (T2 = 0.528) = 1.7978g. The spectral displacement corresponding to the first and second mode periods are sd (t1 = 1.545) = 7.9435 and SD (t2 = 0.528) = 4.9078. The peak response estimated using the response spectrum method can be determined by using

These results are in inches and ve is the additional displacement of the top right corner (beyond the center of mass displacement) in the x direction showing that the influence of the rocking motion in an example where the vertical stiffness of the isolation system is comparable to its horizontal stiffness cannot be ignored. On the other hand, we will show in the following that if the vertical stiffness is much larger than the horizontal, the rocking can be ignored.
If we assume that ω≥o2 we can express the frequencies by
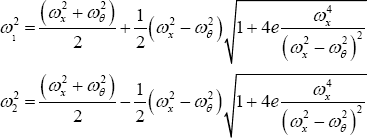
It is clear from these equations that if e = 0, i.e. H = 0 that the two eigenfrequences are ωx and zωg and that the equations of motion are uncoupled but there are other implications from the solutions. If mB > mx the second term within the square root becomes small and when it is expanded by binomial series we get
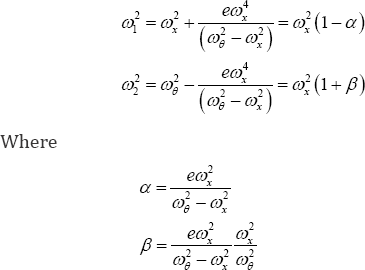
We define the ratio of the vertical and horizontal stiffnesses as 1 = KK and note that X can range up to around 1000 in high shape factor cases. Recalling that 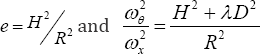 where
where we find that
we find that
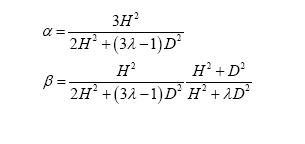
For example, if H=D and λ=100 then α=3/1+3α~~1/λand 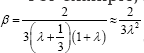 showing that ω1 is almost the same ωx and ω2 is completely unchanged with this value of the ratio between the vertical and horizontal stiffnesses of the isolation system.
showing that ω1 is almost the same ωx and ω2 is completely unchanged with this value of the ratio between the vertical and horizontal stiffnesses of the isolation system.
The results for α and β show the interaction is reduced with increasing vertical stiffness as compared to horizontal stiffness but they also show that the ratio H/D can play a significant role. To illustrate the role of H/d which we denote byp p, we consider the case where the nominal horizontal frequency is fixed so that if the height of the building is increased with the width fixed, the mass is increased at the same rate, as is the bearing horizontal stiffness and the ratio of vertical stiffness to horizontal stiffness X remains constant. The question is: what level of A is needed to ensure that the two modal frequencies m and m2 are changed by the coupling from the nominal by less than a specified tolerance £ (for examples=2%2)? It is clear that the most critical of the frequency shifts is a where
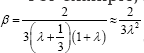
which leads to the rather surprising result that if the height to width ratio of the building is 10 and the tolerance on frequency change is 2% then bearing stiffness ratio must be 5000. This is quite beyond the possibility of rubber bearings showing that rocking is always going to be a problem in tall structures. If the largest possible value of λis 1000 then the height ratio for an ε of 2% is around 4.5.
To illustrate the effect of the height ratio on the eigenfrequencies and the response for specific examples a number of different heights with constant width but fixed horizontal nominal frequency were studied using time history analysis of the record with the response spectrum shown in Figure 7 and in Table 1.
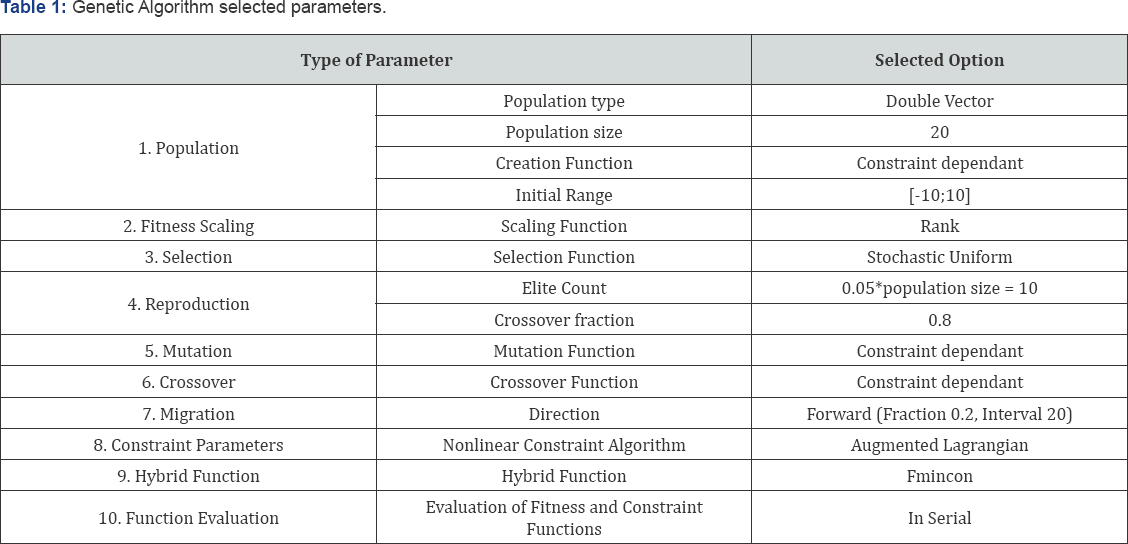
In the system used to show the effect of the height ratio, the ratio of the horizontal and vertical stiffnesses, here defined by zxKKã= were varied from 1 to 500, and the nominal horizontal period of the isolation system was set at 1 second for all height to width ratios implying that the width D is held fixed and the mass M was taken proportional to the height H. With this choice of stiffness's the nominal rocking frequency give by
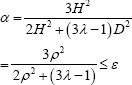
is constant with height, which is counter intuitive. The dynamic properties of this system are given in Table 2a-2c where we see that the lowest frequency, that for horizontal, is very much reduced as the height ratio increases but the rocking frequency is only slightly modified (it is increased).

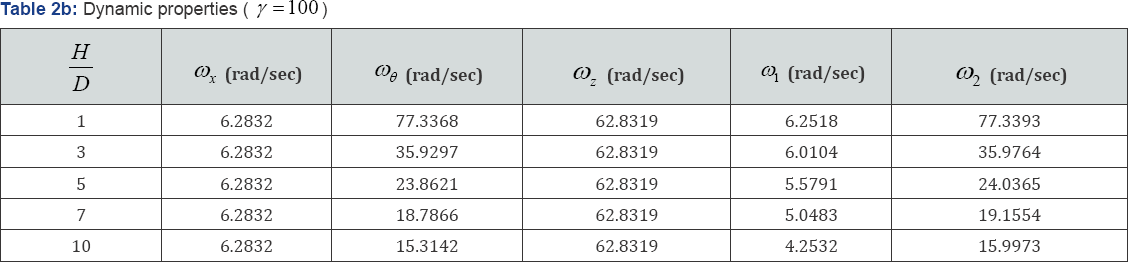
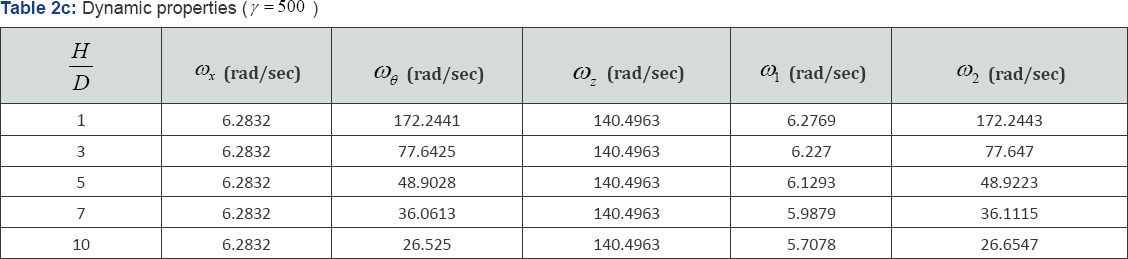
It is clear from these results that as the ratio of the vertical to horizontal stiffness / increases that the changes in frequencies of both the first horizontal mode and the rocking mode become very minimal even for large values of the height ratio.
The response for the horizontal and rocking displacements for the case where the horizontal and vertical stiffness's of the system were the same (y = 1) was estimated by using time history computation with the unscaled El Centro 1940 record and are given in Table 3.

There is an unexpected result that both the horizontal displacement vx, the displacement of the center of mass and the rocking displacement V , the additional displacement at the left hand corner of the block, are maximized at the ratio of 5 but this is due to fact that the record has very little content at the long periods implied by the combined system frequencies for height ratios above 5. This would not happen for a constant velocity design spectrum.
Measured Response of GERB System Building
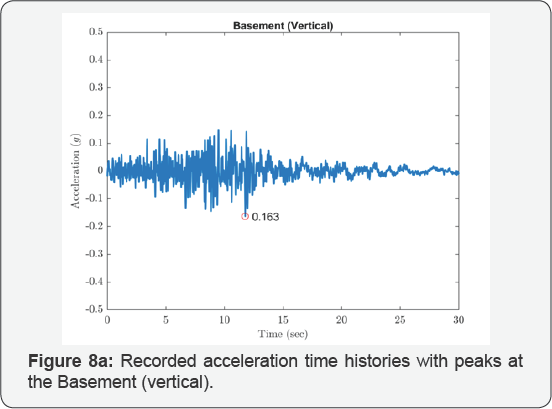
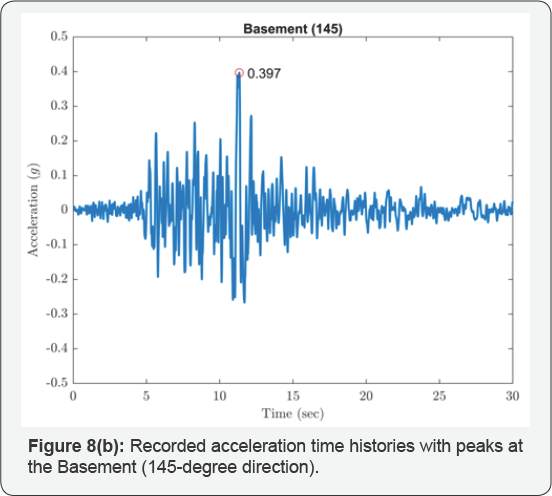
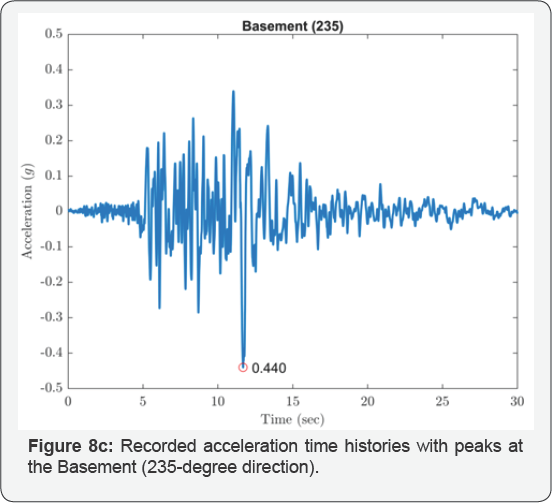
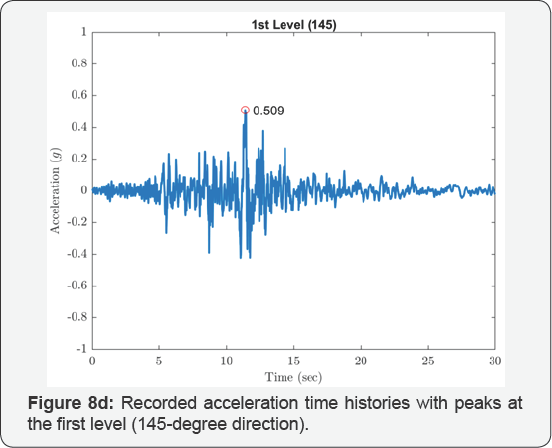

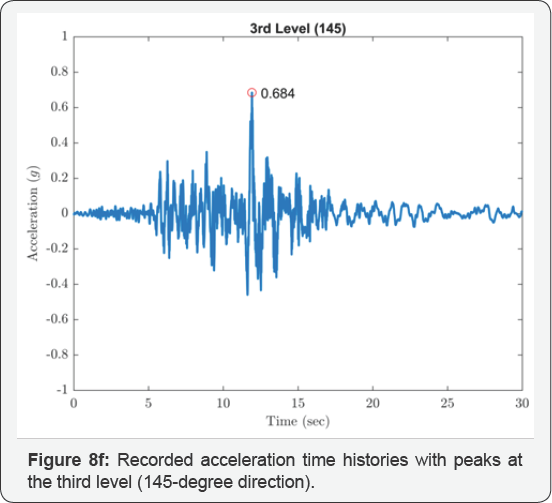
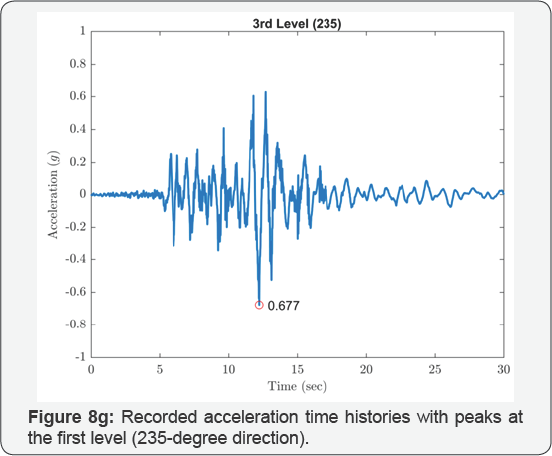

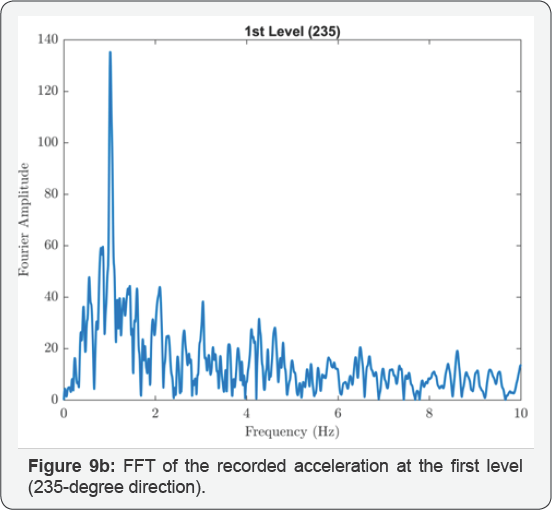
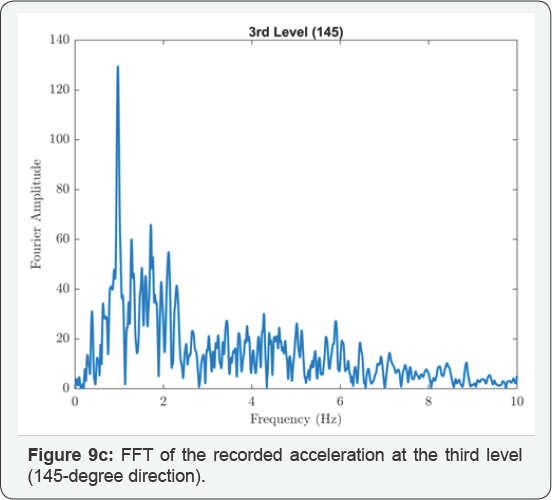
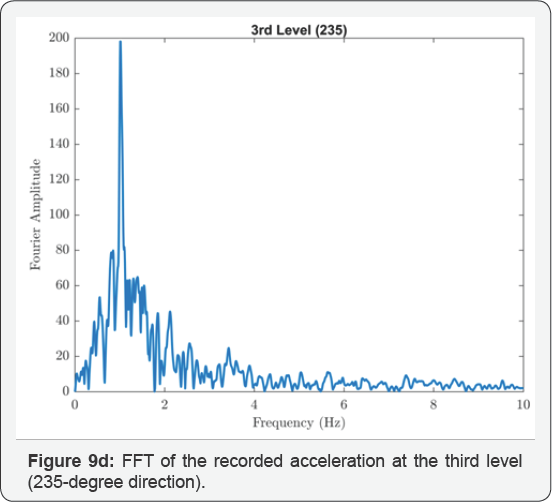
The isolated structures closest to the epicenter of the 1994 Northridge earthquake were two identical 3-story braced steel frame residences in Santa Monica, California, located 22km from the epicenter. Figure 4 shows an overall view of the residences; one of the structures is instrumented by the United States Geological Survey (USGS). Each building is supported at its corners by GERB helical springs and viscous dashpots. Additional springs are distributed around the building perimeters. The design frequencies of the isolation system were 2.5Hz vertically and 1.4Hz in rocking (both directions). Relatively high isolation frequencies were chosen with the intension of limiting the structure displacements to 30mm horizontally and 20mm vertically. Equivalent viscous damping on the order of 25% to 30% of critical was anticipated from the dashpots, and the design anticipated that this level of damping would be sufficient to suppress acceleration amplifications due to resonance. Figure 8a-8g show the recorded acceleration time histories with peaks at the level below the isolators of 0.16g in the vertical direction, 0.40g in the 145-degree direction and 0.44g in the 235-degree direction. Accelerations above the isolation system were generally larger with increased high-frequency content; at the first level the horizontal accelerations were 0.51g and 0.52g in the 145- and 235-degree directions and at the third level 0.68g and 0.68g in these directions. The USGS did prepare a digitized version of these records, but it did not include the vertical component of the records above the isolation system that were impossible to follow; furthermore, the high frequency content in the horizontal records prevented accurate digitization. Using the FFT, the responses above the isolation system show the dominant response was strongly at one second period as shown in Figure 9a-9d. This is most likely to be the rocking frequency for the structure.
The vertical records inside the building are missing from the USGS published results presumably because they could not be digitized but the records from an earlier earthquake that affected the buildings, the Big Bear Earthquake of 1992, have complete vertical records at all three levels. Although small, the earthquake epicenter was distant (132 km), the results for peak acceleration values were quite revealing for this study since the in-structure vertical records were readable. The measured input below the isolation was 11cm/sec/sec vertical and 29 and 22cm/sec/sec in the 145- and 235-degree directions respectively. At the first floor, these were 22, 32 and 22cm/sec/ sec. At the third floor the records were 26, 41 and 24cm/sec/ sec. It seems that the in-structure vertical and the 235 horizontal are about the same as the horizontal input whereas the 145 horizontal is amplified. The vertical at the two floors was much larger than the vertical under the isolation suggesting that the building was rocking about the 235 direction and amplifying the vertical response.

It appears from both the records and from a survey of the buildings performed after the earthquake that the isolation system was not as effective as intended; several architectural and construction details limited movement of the superstructure.
For example, slight damage was observed at locations where steel girders from the isolated portion of the structure framed into both a concrete footing and a masonry block wall attached to the ground (Figure 10). Also, a series of square glass blocks distributed around the perimeter of the structures at the foundation level may have contributed to the large amplifications of the vertical motion. The owner indicated that these blocks were adjusted so that they would be damaged at increments of vertical displacement; the rows of blocks adjusted to 12.5mm and 19mm were broken, while the row of blocks adjusted to 25mm remained intact. This is consistent with the design vertical displacements computed from the acceleration records [8].
It is possible that pounding between these blocks and the foundation of the structure may have led to the high-frequency vertical acceleration spikes. This building has been the only application of the 3-D isolation system to be impacted by an earthquake and to have its response recorded. It has shown very clearly that these systems cannot be used effectively for seismic protection of buildings however useful they may be for vibration isolation.
Conclusion
This paper has covered the history of the search for 3-D seismic isolation in the form of systems using a single component. While all successful isolation systems developed so far have provided only horizontal isolation, the search for an inexpensive approach to a 3-D isolation system has been ongoing for several decades. Many complicated multiple component systems have been developed, mainly for sensitive internal equipment in buildings such as nuclear power plants and chip manufacturing plants, these have proved to be extremely expensive and unsuited for use in most civil structures.
We have shown examples of 3-D systems that have actually been implemented in buildings and have outlined their deficiencies. In the paper, the theoretical basis of the 3-D system has been examined in detail and the cause of these deficiencies, namely the presence of rocking modes has been illustrated. The level of relative vertical flexibility for which a satisfactory performance can be achieved is described. The most likely conclusion of this study is that search for full 3-D seismic isolation has not yet been achieved.
References
- Kelly JM (1988) Base Isolation in Japan, Report No. UCB/EERC-88/20, Earthquake Engineering Research Center, University of California, Berkeley, Calif.
- Tajirian FF, Kelly JM, Aiken ID (1990) Seismic Isolation for Advanced Nuclear Power Stations (with F.F. Tajirian and I.D. Aiken). Earthquake Spectra 6(2): 371-401.
- Staudacher K (1981) Integral Earthquake Protection of Structures, I,II,III, Eidgenossische Technische Hochschule, Institute furBaustatik and Konstruktion, Zurich, Switzerland.
- Staudacher K (1984) Structural Integrity in Extreme Earthquakes, The Swiss Full Base Isolation System (3-D). 8th WCEE, San Francisco 5: 1039-1046.
- Garevski M (2010) Development, Production and Implementation of Low Cost Rubber Bearings. In M Garevski, A Ansal Earthquake Engineering in Europe. Springer Science+Business Media B.V.
- Gjorgjiev I, Garevski M (2012) Replacement of the Old Rubber Bearings of the First Base Isolated Building in the World. 15th World Conference of Earthquake Engineering 2012 (15WCEE).Lisbon, Portugal.
- Huffmann GK (1985) Full Base Isolation for Earthquake Protection by Helical Springs and Viscodampers. Nuclear Engineering and Design 84: 331-338.
- Makris N, Deoskar HS (1996) Prediction of Observed Response of Base- Isolated Structure. Journal of Structural Engineering 122(5): 485-493.
- Kelly JM, Tajirian FF (1989) Mechanics of Low Shape Factor Elastomeric Seismic Isolation Bearings, Report No. UCB/EERC-89-13, Earthquake Engineering Research Center, University of California, Berkeley, Calif.






























