Open AccessJournals | List of Open Access Journals

Research Article

Statistical Analysis of Vehicle Crashes on Mississippi Coastal Two-Lane Highways

Zhao Ma, Ningning Wang and Feng Wang*

Dept. of Civil & Environmental Engineering, Jackson State University, Mississippi

Submission: December 27, 2017; Published: March 05, 2018

*Corresponding author: Feng Wang, Dept. of Civil & Environmental Engineering, Jackson State University, Jackson, Mississippi 39217, Tel: 601-979-1094; Fax: 601-979-3238; Email: feng.wang@jsums.edu

How to cite this article: Zhao M, Ningning W, Feng W. Statistical Analysis of Vehicle Crashes on Mississippi Coastal Two-Lane Highways.Civil Eng Res J. 2018; 3(5): 555622.DOI:10.19080/CERJ.2018.03.555622

Abstract

The traffic fatality per capita of Mississippi has been at about twice the national average level in the last five years. Although tremendous efforts have been made to develop the State Highway Safety Plan, limited attention has been paid to good understanding of the characteristics of the crashes in Mississippi. Due to the relatively high percentage of heavy trucks in and out of the seaports, the traffic crashes on two-lane county roads of the coastal area are suspected to be more severe. A binary logistic regression model is developed to expose the factors that contribute to the crash severity on the two-lane county roads of the Mississippi coastal area. The study conducts statistical analyses using the crash data of the past three years to find possible relationships between crash severities on these two-lane highways and the factors or combinations of factors of time of day, environment, roadway, vehicle, driver, and driver behavior. The analysis results indicate that those crashes that involved with vehicles, dark lighted and dusk or dawn light conditions, drivers with no driver license or suspended driver license, high speed, speeding, and none restraint usage or helmet usage, tend to increase the probability to be more severe crashes. On the other hand, it is also presented that male drivers decrease the likelihood of fatal or injury crashes. The predictive power of the model is tested under 10-fold cross validation. The results show that the model has significantly higher predictive power than a non-information guess.

Keywords: Two-lane highway; County roads; Binary logistic regression; Crash severity; Cross validation

Introduction

Significance of study

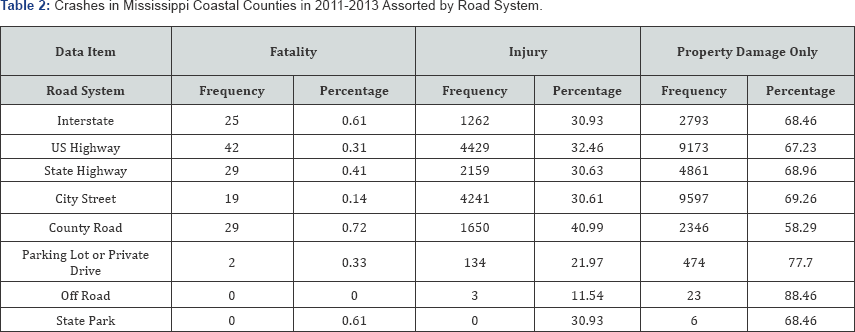
Vehicle crashes are considered among top 10 leading causes of deaths in the United States. According to the data from the National Highway Traffic Safety Administration (NHTSA), more than 30,000 people died from vehicle crashes every year since 1949. The numbers of people that died from vehicle crashes are 32,479, 33,782, and 32,719 during the years 2011, 2012, and 2013, respectively, while the numbers of people who were injured in these three years are 2,217 2,362 and 2,313 thousands, respectively [1]. Vehicle crashes, which take a major weight of traffic safety, have been a nationwide focus in the United States. The current traffic safety situation in Mississippi has been of great concerns. From Table 1, it is indicated that vehicle crashes caused around 600 fatalities in Mississippi each year in the past three years. But the fatality rate per capita, calculated at around 20 fatalities per 100,000 population which is almost twice as high as the US average level, is actually among the highest in the country. The fatality rate assessed at over 1.5 fatalities per million vehicle miles travelled (VMT), is also much higher than that of the nationwide average. The NHTSA's Traffic Safety Facts: State Traffic Crash Data have shown that the fatality rate is decreasing over the past decades. The fatality rate per million VMT also decreased by 58% from 1975 to 2013 in Mississippi. However, considering the original high level and the nationwide decreasing trends (The fatality rate per VMT in the US decreased by 67% in the same time period), Mississippi is still among the top states in traffic crash rate. All these facts clearly indicate that the traffic safety situation in Mississippi is still severe. Three Mississippi coastal counties, Harrison, Hancock, and Jackson, which have a total population around 400,000 out of the approximately 3 million population in 82 Mississippi counties in the state, are areas with high values in both population and vehicle crash fatalities. Gulfport is located at the center of the Mississippi coast and the second largest city in Mississippi after the state capital Jackson. High freight traffic is generated due to the transshipping of freight from cargo vessels to trucks and intermodal operations at Port of Gulfport, which is No. 19 in the US in terms of containership and among the top 50 US ports by port calls and vessel type [2]. Table 2 was derived from vehicle crash records collected by the Mississippi Department of Transportation (MDOT) in year 2011-2013, which would explain the motivation of this study. From Table 2, it can be shown that county road is the road class with the highest fatality rate and injury rate. Among the 4025 crash records on Mississippi coastal county roads, 3684 (91.53%) were on 2-lane highways, which indicates that 2-lane county roads are hazardous spots that entail more attention. Mining out factors that contribute to more frequent and severe crashes would be the first step to improve the undesirable situation on 2-lane highways of the Mississippi coastal area.

Statistical models

In the past twenty years, numerous studies have applied statistical models on crash analysis. Traditionally, negative binomial models have been applied to assess highway safety based on crash counts and crash rates [3-8]. Crash frequency models were developed for each collision type [3]. They analyzed the individual collision types by comparing the aggregate model results. The results indicated that annual daily traffic (AADT), lane number, and the presence of turning lanes were positively related with all collision types, while median width and light condition were negatively related with different collision types. However, Pande and Abdel-Aty [9] pointed out the limitations of the negative binomial models. Lengths of the segments selected to aggregate the crash data were hard to be determined. There was not an agreeable way of optimizing the selection of the segment lengths for crash studies.

Logistic regression models have been widely used in analyses of crash severity as a response variable. Dissanayake and Lu [10] modeled crash severity for single-vehicle fixed object crashes involving young drivers. By using sequential binary logistic regression, they modeled the crash severity wit five categories, which were no injury, possible injury, non-capacitating injury, incapacitating injury and fatal. Factors such as alcohol or drug influence, ejection in the crash, point of impact, rural locations, curved or graded crash location and speed of vehicle significantly increased the probability of more severe crashes. Restraint device usage and male drivers were considered to reduce the crash severity level. It was also found that factors such as weather, residence location, and physical condition did not have significant influences on crash severity using this model. Binary logistic regressions have been used when the response variable is binary. Lui et al. [11] presented significant findings modeling crash severity with a multivariate approach. Shanker et al. [3] developed a predictive model of crash severity with a nested logit model. Kusano & Garbler [12] tested the predictive power of logistic regression and machine learning, and concluded that logistic regression slightly outperformed machine learning. The authors also mentioned that the improvement of prediction accuracy is very meaningful to reduce the odds of death by guiding the trauma team to take seriously injured occupants into a trauma center to receive necessary treatments.

The objectives of this paper are to identify the factors that are likely to lead to more severe crashes, and to build up a predictive model which can significantly increase the prediction accuracy of the crash severity. The organization of the paper is as follows: after the Introduction section, the Methodology section presents the multivariate logistic regression model and model validation, followed by description of the data used in the analysis. In the Data Analysis and Results section, the variable selection in the data analysis process and regression analysis results are presented followed by careful checks and discussions on the prediction power of the regression model used for the study. Finally findings of this study are summarized in Conclusions.

Methodology

Logistic Regression Model

Logistic regression is one of the popular regression methods which describe the relationship between explanatory variables and a discrete response variable. The explanatory variables can be either categorical or numerical, or a mixture of both. The model is generally used to handle categorical variables. A binary logistic regression is good to use when the dependent variable is a bivariate. In this study, the dependent variable can only take on two values: y = 1 for fatality or injury, and y = 0 for property damage only. The probability that a fatality or injury takes place is modeled as logistic distribution by Equation (1):

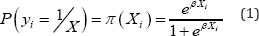
And the logit of the binary logistic regression model is presented in Equation (2):

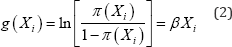
Where p (.) stands for the probability of a severe accident (y_i= 1); X_i is the vector of independent variables for thei^th observation; (x_i) is the conditional probability of a fatality or injury that occurs when an accident is present; is the coefficient vector, which directly determine the odds ratio involved in the fatality or injury; g(x_i) is the link function.

The odds ratio for the j^th independent variable that is equal to e^βj represents the relative value by which the odds of the fatality or injury increase or decrease when the value of the j^thpredictor is increased by 1.0 units.

The estimation of the coefficient vector is processed by the maximum likelihood method [13].The likelihood function is given by Equation (3):

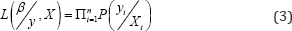
Where L (.) stands for the maximum likelihood a crash severity given the observed data. Combine Equations (2) and (3), noting that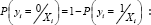

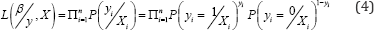
Taking logs, the log-likelihood function can be written as follows:

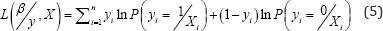
Iterations were applied to maximize the log-likelihood function and achieve the estimation of the coefficient vector. Due to the complex computation, the open source statistical analysis software R program was adopted to conduct the estimation of the coefficient vector in this study.

Different plausible models were built and tested for goodness of fit using the Wald chi-square measures, and the best fitted model was selected as the final model. A set of null and alternative hypotheses were assumed to construct different models and tested in the Analysis of Variances (ANOVA). Specifically, under the null hypothesis, the reduced model is the adequate model while under the alternative hypothesis the full model is the adequate model. Iteratively the full model is reduced based on each of the hypothesis tests, while the Wald chi-square test was applied to determine whetherb or not to statistically reject the null hypothesi based on the pre-selected p-value for the level of significance.

Model validation

The 10-fold cross validation process was applied in this study to test the predictive power of the selected model. If the predictors are trained to a dataset and then the same data are used to test the model's accuracy, and the model that over-fits the dataset is generally considered to have the best performance. However, this classifier may perform poorly comparing to a more flexible classifier with new data [12]. The 10-fold cross validation method was adopted in order to eliminate the overly optimistic estimates of model performance.

The procedure of 10-fold cross validation includes:

1) divide the dataset into 10 even subsets;

2) use 9 subsets to train the model and 1 subset to test the model; and

3) repeat the steps in 1) and 2) for10 times until all subsets are tested as the testing dataset.

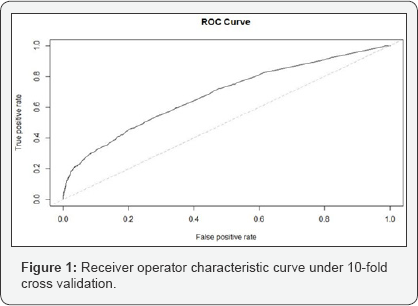
In this study, the receiver operator characteristic (ROC) curve and confusion matrix are used to show the predictive power of a logistic regression model. ROC curve, which consists of the true positive rate and false positive rate, has the advantage of showing the predictive power in a stable shape, while the confusion matrix exposes the predictive power numerically and in a straight forward manner.

Dataset

The data for this study were provided by the Mississippi Department of Transportation (MDOT). The original dataset consists of vehicle crash records in Mississippi for years 2011, 2012, and 2013. The dataset with 3684 usable observations was achieved by screening and cleansing the data for crashes on Mississippi coastal county roads.

Seven types of crash information were used that included: 1) crash data, 2) temporal data, 3) environment data, 4) road data, 5) vehicle data, 6) driver data, and driver behavior data. The crash data includes severity and number of vehicles involved. Temporal data is equivalent to day of week and time of day. Environment data contains light condition, weather, and road surface condition. Road data consists of whether or not at an intersection and pavement surface material. Vehicle data shows vehicle type. Driver data provides information of driver's age, gender, race, and driver licensure status. Driver behavior data refers to estimated speed, speeding, and restraint usage. Table 3 shows the frequency and percentage of explanatory variables. A total of 3864 records were retrieved for the county roads in the Mississippi coast, with 1549 fatal or injury records and 2135 property damage only records.

The missing values and unreasonable data were removed during initial data processing. The removed data represented a small proportion of the dataset, which means removing them would not lead to bias in data analysis and unreliable analysis results.

Data Analysis and Results

Variable selection

The R program was applied to process and analyze the data in the following 4 steps. First, all variables were included in the binary logistic regression model to test the significance of every variable. Then, variables with values larger than >0.05 were removed iteratively to fit the reduced models. The third step is to conduct the likelihood ratio test to determine if we need to reject the null hypothesis that the reduced model is true. Repeat the above steps until the reduced model was rejected and the process of selecting variables for the regression model is then terminated. Table 4 shows the analysis results for variable selection, which are described in the following paragraphs. Table 5 presents the ANOVA results obtained from the R program. As shown in the table, Model No. 3 is the final model in our study. It includes variables with at least one significant category. However, age was an exception due to the relatively small proportion (2.74%) of the significant category for drivers aged 75 and above. Removing insignificant variables can prevent unnecessary disturbance without losing the predictive power of the model.

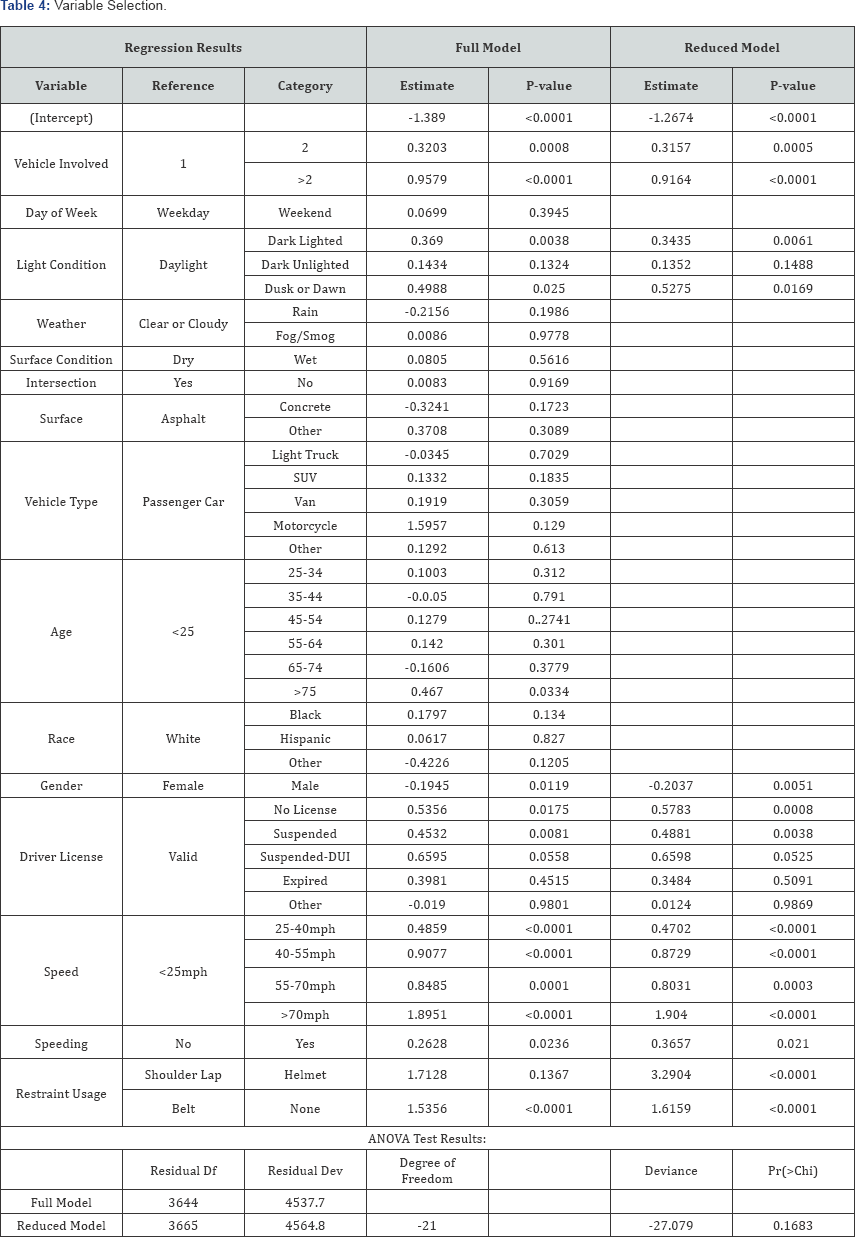
Binary logistic regression results

The odds ratios (OR) for the final predictive model are shown in Table 6, which stand for the ratios of log probabilities of involving in a fatal or injuring crash of a category over the reference category of a selected independent variable. Table 6 also lists the estimated coefficients (B) of the selected variables and the categories of the variables to predict the log probabilities of a severe crash. The coefficients are actually the log probabilities of a severe crash occurring due to the independent variables, and each coefficient stands for the change in the log probability of a severe crash associated with one-unit change in the independent variable. The seven variables retained in the final model include the number of vehicles involved, lighting condition, gender, driver license, estimated speed, speeding, and restraint usage. The effects of the seven independent variables in the model are discussed in the following paragraphs.

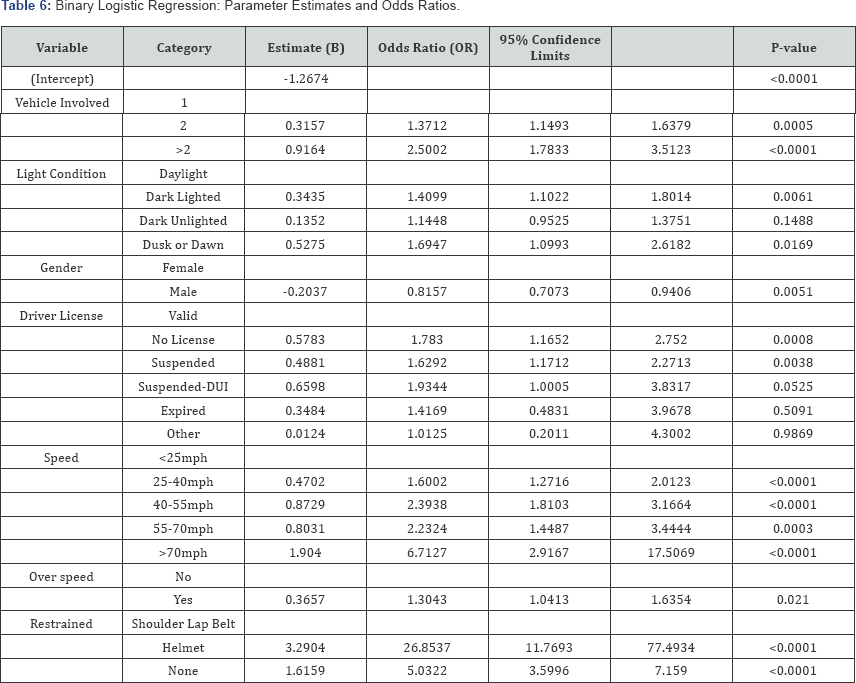
Vehicles involved: All things being equal, the OR results indicate that the log probability ofhaving a severe (fatal or injuring) crash due to a crash involved with two vehicles is 1.3712 times as much as the log odd of crashes due to only single vehicles. Similarly, the crashes involving with more than two vehicles have a log probability of a fatal or injure severity 2.500 times the log odd of the crashes involving with only single vehicles.

Light Condition: A light condition has four categories. The OR value indicates that the log probability of having a fatal or injury accident due to a dark light condition is 1.4099 times that due to a daylight condition. Similarly, the log probabilities of having a fatal or injury crash due to dark unlighted condition and dusk or dawn condition are 1.14 and 1.69 times that due to a daylight condition respectively. The reason why the dark lighted and dusk or dawn conditions increase the probability of a fatal or injury crash might be because of the misestimate of vision loss under these conditions. Being aware of vision loss under a dark unlighted condition, the drivers would tend to pay closer attention to the road condition and drive more carefully, therefore could reduce the severity level of a crash.

Gender: Compared with female drivers, male drivers are statistically less likely to be involved in a fatal or injury crash, with an odd ratio of 0.8157.

Driver license: The results show that a driver with an expired driver license is not statistically significant for a severe crash. However, a driver without a driver license or with a driver license suspended is statistically significant for a severe crash. Compared with a validly licensed driver, the odd ratios of the log probability of involving in a fatal or injuring crash, for a driver without a driver license and a driver with a driver license suspended are 1.78 and 1.63 respectively.

Speed: Compared with the reference speed category of less than 25 mph, all other 4 categories are statistically significant in involvement with a severe crash. Compared with the reference speed category, the odds ratios of the log probability of involving in a fatal or injuring crash, for driving speeds at 25-40 mph, 40-55 mph, 55-70 mph, and over 70 mph are 1.6002, 2.3938, 2.2324, and 6.7127 respectively. Obviously this analysis result shows that the higher the driving speed, the larger the probability of involving in a fatal or injury crash.

Speeding: The odds ratio of 1.3 in involvement of a fatal or injury crash of a speeding behavior over the non-speeding driving with respect to the speed limit well indicates that speeding in driving is statistically significant in causing a severe crash.

Restraint usage: The usage of shoulder lap belt is set to be the reference category. The odds ratio of helmet usage at 26.85 actually indicates that a motorcycle driver wearing a helmet is 26.85 times more likely to be in a fatal or injury crash, compared with the log probability of a driver utilizing shoulder lap belt involving a severe crash. The odds ratio of a driver with no restraint usage at 5.03 well indicates the great importance of restraint usage in avoiding fatality and injury in driving.

Prediction power

As shown in Table 7, the confusion matrix under the 10-fold cross validation method has measured the predictive power of the final model developed in the binary logistic regression. The accuracy of the prediction at 0.6509 is significantly higher than the non-information guess at a value of 0.5795, which indicates that the logistic regression has a significantly higher predictive power than a non-information guess. The receiver operator characteristic (ROC) curve was also plotted to present the predictive power. The advantage of ROC curve is its stability in shape. The area under curve (AUC) is the index to evaluate ROC curve. A larger AUC means better predictive power. Figure 1 presents the AUC of the ROC curve of this logistic regression model which was assessed at 0.6805.

Conclusion

This study uses a binary logistic regression model to identify the factors that possibly contribute to the crash severities on two-lane county roads in the Mississippi coastal area. Vehicle crash severity is considered as dependent variable. Seven types of data, which include crash data, temporal data, environment data, roadway data, vehicle data, driver data, and driver behavior data are the explanatory variables used in predicting crash severity. The analysis is conducted using the R program. The variables with at least one category statistical significance were retained in the final model.

As discussed in the paper, the analysis results indicate that compared to single vehicle crashes, the crashes that involved with two or more than two vehicles have a higher probability to be fatal or injury crashes. It is shown that dark lighting and dusk or dawn, as compared to daylight, increase the probability of fatal or injury crashes. Males are found to be less likely to be involved in fatal or injury crashes. Drivers without driver license are more likely to be in more severe crashes. Drivers with driver license suspended, especially suspended due to DUI, have a larger chance to be in fatal or injury crashes. The probability to be in fatal or injury crashes is greater with a higher vehicle speed. Speeding also leads to more severe crashes. The restraint usage greatly impacts crash severity. No restraint usage apparently increases the probability of fatal or injury crashes. Compared with car driving, motorcycle driving even with helmets on are much more prone to severe crashes. The confusion matrix under the 10-fold cross validation method shows that the binary logistic regression model has a significantly high predictive power than a non-information guess.

Acknowledgement

The project received research funding support from the Institute for Multimodal Transportation (IMTrans) at Jackson State University. The IMTrans is member of the Maritime Transportation Research and Education Center (MarTREC) with the University of Arkansas (lead), Louisiana State University, and the University of New Orleans. MarTREC is one of the Tier I University Transportation Centers funded by the US DOT. Traffic engineers Christopher Kimbrell, Jim Willis, James Sullivan, and Wes Dean at the Mississippi Department of Transportation are thanked for providing data support to the study.