Linear Elastic Lateral Buckling (Including Shear Deformation) and Linear Elastic Lateral Torsional Buckling of Composite Beams - an Analytical Engineering Approach
JPBN Derks*
*Department of civil, FE IT Consultant, Netherlands
Submission: September 22, 2017; Published: January 09, 2018
*Corresponding author: J. P. B. N. Derks, FE IT Consultant, Hoofdmanweg 10 NL-4871 LD ETTEN-LEUR the Netherlands, Tel :+31-76-5140023; E-mail: info@feitconsult.nl
How to cite this article: JPBN Derks. Linear Elastic Lateral Buckling (Including Shear Deformation) and Linear Elastic Lateral Torsional Buckling of Composite Beams -an Analytical Engineering Approach. Civil Eng Res J. 2018; 3(1): 555604. DOI: 10.19080/CERJ.2018.03.555604
Abstract
This article outlines a concise and complete versatile novel analytical framework to quickly and effectively assess lateral shear (knik) and lateral torsional buckling (kip) of composite beams build of sections with different lengths. The adjective "composite” includes dissimilar beam cross-sections (beam profiles) and distinct beam materials. The major aim is to provide engineers with an accurate, simple but elegant, practically applicable and analytical beam buckling tool based on advanced solid theoretical propositions or background. The justification of the analytical theory is supplied by demonstration of executed numerical tests (i.e. finite element method), which affirm the validity of the proposed analytical buckling models adapted to the considered beam buckling cases.
Keywords: Lateral buckling; Lateral torsional buckling; Composite beam; Analytical formulation; Shear deformation; Linear elasticity
Introduction
Buckling means the loss of stability of an equilibrium configuration of a structure. Elastic buckling is a state at which the structure loses its stability and large elastic deflections will start developing rapidly. It is normally associated with the minimum eigen value of the perfect structure, i.e. often referred to as classical buckling [1]. In this article attention is confined to linear elastic composite beam buckling (especially lateral and lateral torsional buckling phenomena). An abbreviated and lucid literature survey and comprehensive discussion about lateral and lateral torsional buckling of structural members is rendered in the dissertation of Raven [2] and the article of Vander Put [3]. It should be highlighted that the adjective "composite” refers to multiple beam cross-sections and beam materials.
Approximate solution methods are frequently encountered and used in engineering design practice for tackling beam buckling problems. In particular, summation theorems (i.e. Foppl Papkovich theorem) are appropriate and advantageous because of their robustness, accuracy, easiness and algebraic simplicity [4]. It should be kept in mind that there is similarity or analogy with parallel and serial analytical approaches of spring systems, electric systems or hydraulic systems (the so-called analogies).
The key goal of this article is to address respectively formulate an effective analytical tool for reliable (engineering) estimation or approximation of the linear elastic lateral shear buckling force and linear elastic lateral torsional buckling moment of composite beams made of non-overlapping parts based on the indicated summation theorem and corresponding well-established structural elastic stability notions [5]. A succinct but detailed exposition of the previous stated matters and issues is offered in the subsequent sections.
Preliminaries and Requisites
Global Cartesian ( components) and local Cartesian ( components) right-handed coordinate systems are used. The former identify the composite beam orientation, beam location and beam external loads, while the latter define attached geometrical (shape and size) properties of the homogenous beam cross-sections. It is henceforth assumed that the origin of the local coordinate system is located at the centroid C of the cross-sectional area. In addition, the initial (undeformed) geometry of the composite beam is a straight line. The following beams cross sectional quantities (properties) are employed [6].
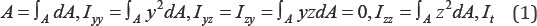
Where,
A is the cross sectional area,
Iyy , Iyz , Izy and Izz are called second moments of area.
Where, It is the torsion constant.
Note 1: The centroid C is defined as that point of an area A for which the static moments of area are zero when the origin of the local xyz coordinate system is chosen there, i.e.
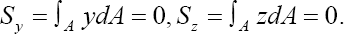
The normal centre NC is specified as that point of the crosssectional area where the resultant of all normal stresses due to extension has its point of application.
Note 2: In a homogenous (single material) cross-section, the centroid C and normal centre NC coincide.
Note 3: The adopted assumption I yz = Izy = 0 implies that the selected beam cross section has at least two lines of symmetry.
Note 4: I yy and Izz are commonly indicated as the moments of inertia and I yz , I zy are known as the product of inertia. The Equations (1) have been applied to the cross-sections in Figure 1. The results are Shown below.



Linear elastic lateral buckling (including shear deformation) (knik)
Model geometry
The typical model geometry is depicted in Figure 2. The following mechanical boundary (displacement and load) conditions are implemented (prescribed).
Boundary 1: uX = O, uY = O, uz = O , Fx = l (applied at centroid)
Boundary 2: uY = 0, uZ = 0 , FX = -1 (applied at centroid)
Note 1: A set of balanced forces is obligatory in order to preserve equilibrium of the composite beam in the analytical model configuration.
Note 2: The prescribed boundary displacement constraints prevent rigid body motions (circumvent singularities in the numerical (finite element) solution process).
Analytical model
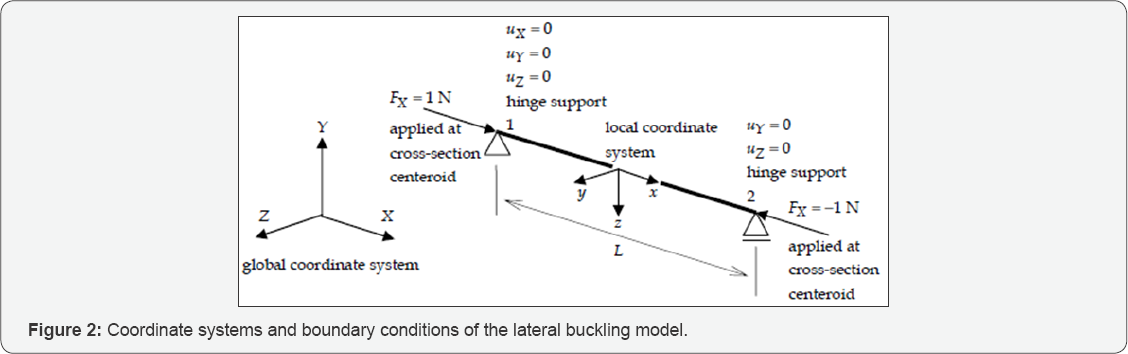
The composite beam with length L is made of segments i with corresponding length Li (Figure 3) and each segment (section) i has the accompanying attributes Young's modulus Ei shear modulus Gi , shear deformation coefficient ksi [7,8] crosssection area Ai and second moment of area Ii Furthermore, the cross-section of each segment i fulfils the condition Iyyi < Izzi , which implies that Ii=Iyyi Consequently, the following relation holds.
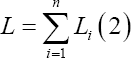
The engineering estimate of the buckling length Ltmci segment i is given by the expression
Lbuci = kbucLi (3)
Where,
Kbuc Is the buckling length factor, which is identical for each segment in the particular composite beam arrangement.
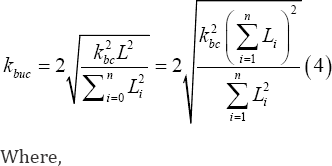
Kbc Is the buckling length factor of the composite beam, dependent on the mechanical boundary conditions (supports). In this specific case of a composite beam with span L and supported by two hinges at the edges k bc = 1.
It is emphasized that the buckling length of the composite beam depends only on the boundary conditions and thus not on cross-sectional properties. Substitution of Equation 4 into Equation 3 produces the following identity.
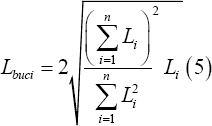
Subsequently, the linear elastic lateral shear buckling force Fbuci of segment i is universally elaborated as shown in Equation 6a. Note that shear deformation is also incorporated, see [5], (Timoshenko 1985).
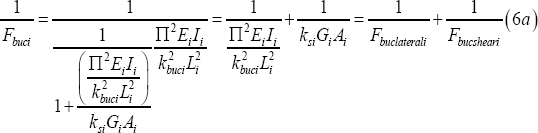
Fbuc Is the linear elastic lateral shear buckling force of segment i,
Fbuclaterali Is the linear elastic lateral buckling force of segment i,
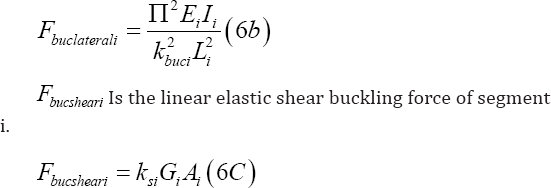
Recalling from literature that the Foppl-Papkovich theorem (Tarnai 1995) is valid for this case, the following lateral shear buckling system force equation is stated in general format.
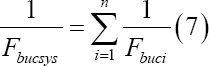
Fbucsys Is the linear elastic lateral shear buckling force of the composite beam (also denoted as system), n Is the total number of considered segments.
The aforementioned formulae devise the complete linear elastic lateral shear buckling analytical model.
Numerical verification (case studies) knik
Three case studies (KNIK 1, KNIK 2 and KNIK 3) are conducted and concisely presented in order to examine the validity and soundness of the proposed analytical approach by comparison with numerical results obtained by the finite element method [9,10].
Case study KNIK 1-1
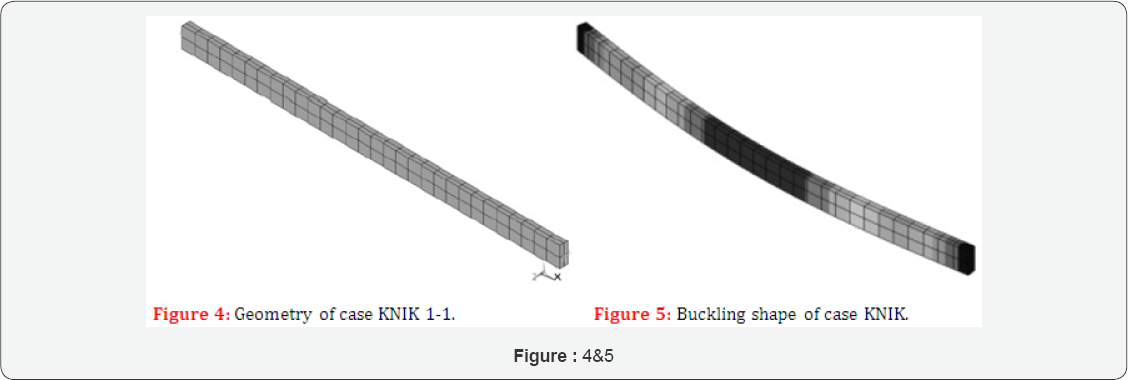
Case KNIK 1-1 considers a wooden beam of one segment (Figure 4).
The properties are L = 3000 mm, L1 = 3000 mm, Kbuc = 1,Kbc = 1,FX=±N,
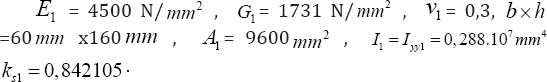
The obtained results are Fbucsysnumerical =14214N and Fbucsysnumerical = 14221N (Figure 5).
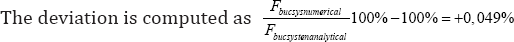
Case study KNIK 1-2
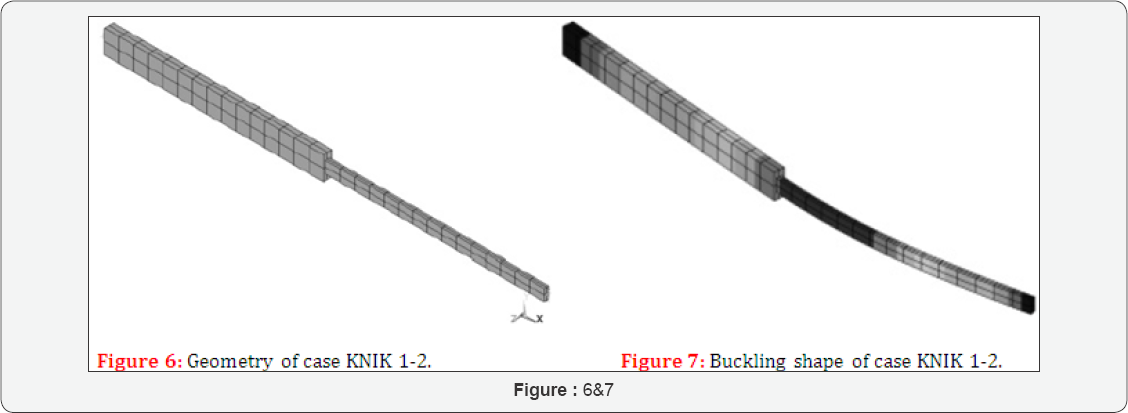
Case KNIK 1-2 considers a composite wooden beam of two segments (Figure 6).
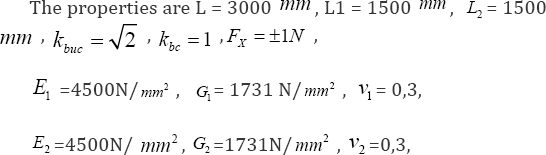
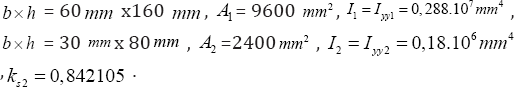
The results are Fbucsysamlytical =I673N, Fbucsysnumerical= I443N (Figure 7). The deviation is -13, 74 %.
Case study KNIK 1-3
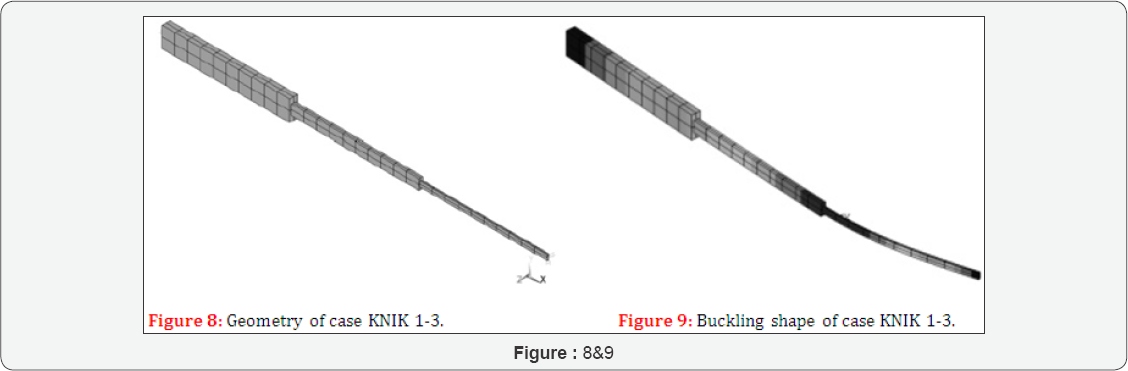
Case KNIK 1-3 considers a composite wooden beam of three segments (Figure 8).
The properties are L = 3000 mm, L1 = 1000 mm, L2 = 1000 mm, L3 = 1000 mm,
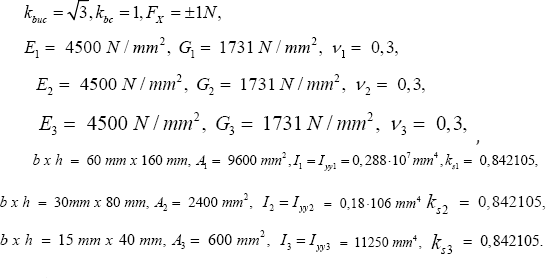
The results are Fbucsysanalytical =156 N and Fbucsysnumerical = 161 N (Figure 9). The deviation is +3, 11 %.
Case Study KNIK 2-1
Case KNIK 2-1 considers a steel beam of one segment (Figure 10).
The properties are L = 3000 mm, L1 = 3000 mm, Kbuc = 1,Kbc = 1,FX=±N,
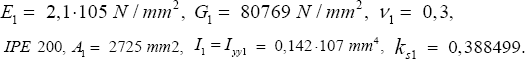
The obtained results are Fbucsysnumerical =328263N and Fbucsysnumerical = 326493N (Figure 11).
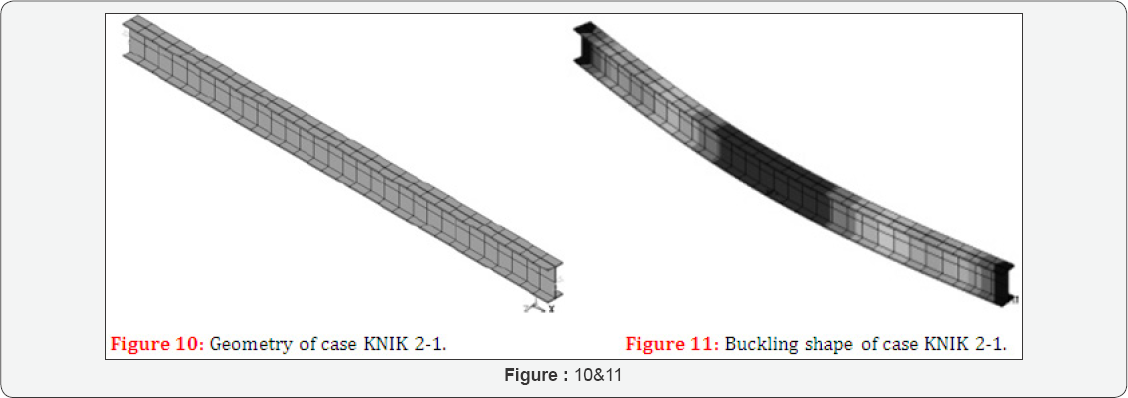
The deviation is -0,539 %.
Case Study KNIK 2-2
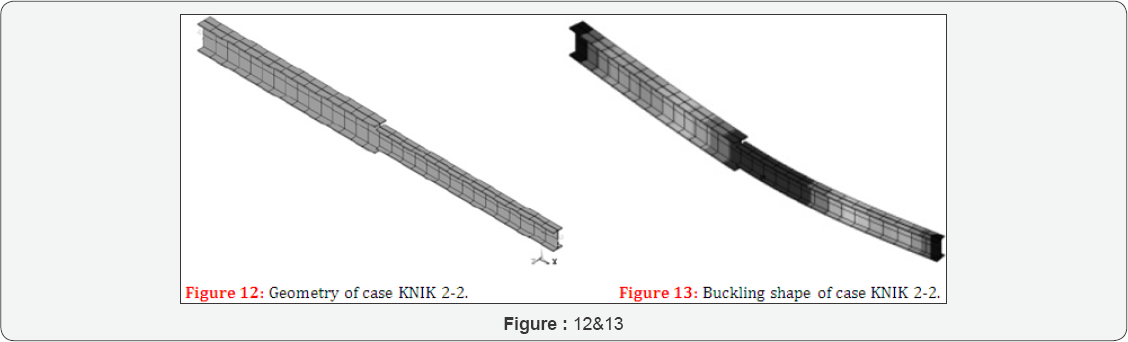
Case KNIK 2-2 considers a composite steel beam of two segments (Figure 12).
The properties are L = 3000 mm, L1 = 1500 mm, L2 = 1500 mm, kbuc = 2, kbC = 1, FX = ±1 N,
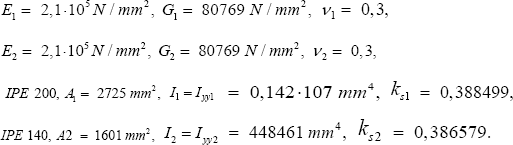
The results are Fbucsysnumerical = 157757N and Fbucsysnumerical= 147745N (Figure 13) the deviation is -6,346%.
Case Study KNIK 2-3
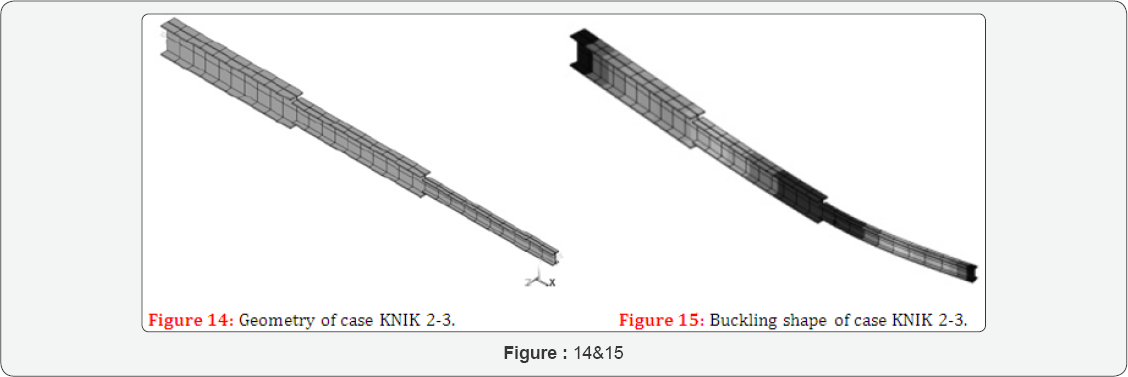
Case KNIK 2-3 considers a composite steel beam of 3 segments (Figure 14).
The properties are L = 3000 mm, L1 = 1000 mm, L2 = 1000 mm, L3 = 1000 mm,
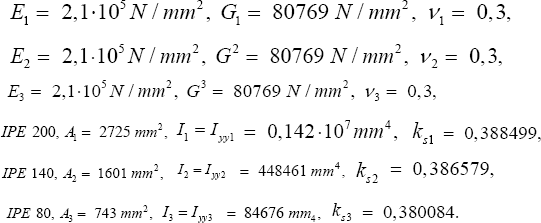
The results are Fbucsysanalytical = 47024N and fbucsysnumerical= 48983N (Figure 15). The deviation is +4,165 %.

Case Study KNIK 3-3
Case KNIK 3-3 considers a composite steel-wood beam of three segments (Figure 16).
The properties are L = 3000 mm, L1 = 1000 mm, L2 = 1000mm,L3 = 1000 mm,
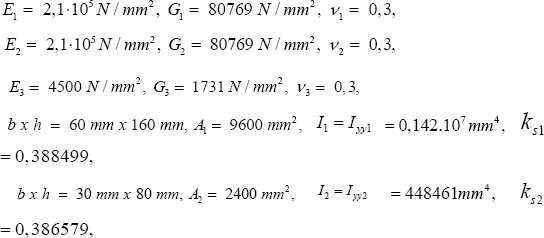
The results are = 166 N and = 171 N (Figure 17). The deviation is +3,012 %.
Linear elastic lateral torsional buckling (kip)
Model geometry
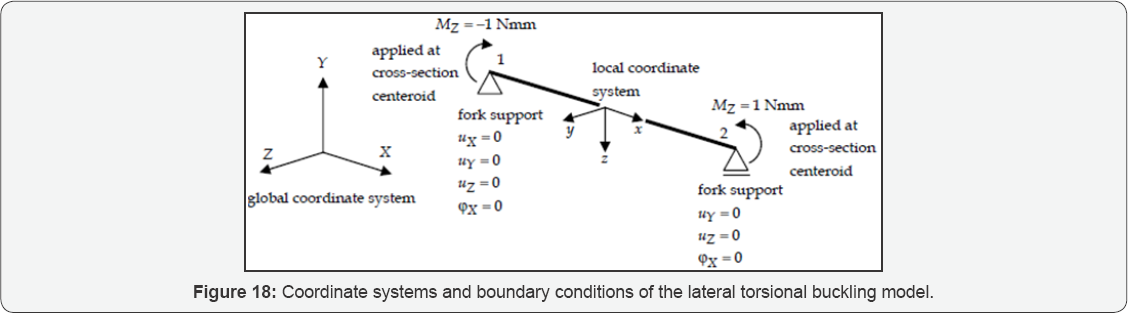
The governing model geometry is shown in Figure 18. The following mechanical boundary (displacement and load) conditions are implemented (prescribed).
Boundary 1: ux = 0 uy = 0 uz = 0 , φx = 0, Mz = -1 (applied at centroid).
Boundary 2: uy = 0 uz = 0 , φx = 0,
Mz = +1 (applied at centroid).
Analytical model
The model for lateral torsional buckling is mostly identical to the models for lateral buckling (Section 7.2). Not used in lateral torsional buckling is the shear deformation coefficient ks1. Extra is the is the torsional constant Iti,. The cross-sectional warping stiffness of segment i is assumed to be negligible. The engineering estimate of the buckling length Lbuci of segment i is
Lbuci = kbucLi (8)
Where,
kbuc Is the buckling length factor. Which, is the same for each segment in the specific composite beam configuration
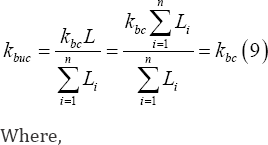
kbuc Is the buckling length factor of the composite beam, dependent on the mechanical boundary conditions (support). In this specific case of a composite beam with span L and supported by two forks at the edges:
kbc = 1
It is underlined that the buckling length of the composite beam is only dependent on the boundary conditions and hence not on cross-sectional properties. Substitution of Equation 9 in Equation 8 produces the following identity.
Lbuci = kbucLi (10)
Taking into account the previous settled propositions, the linear elastic lateral torsional buckling moment Mbuci of segment i is
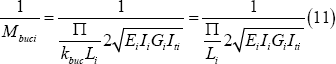
The Föppl-Papkovich theorem (Tarnai 1995) is apt for this case. The following lateral torsional buckling system moment equation is written in universal layout.
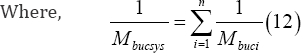
Mbucsys Is the linear elastic lateral torsional buckling moment of the composite beam (also symbolized as system).
n is the total number of segments.
The aforesaid procedure details the full linear elastic lateral torsional buckling analytical model.
Numerical verification (case studies) kip
Three case studies (KIP 1, KIP 2 and KIP 3) are consecutively undertaken and compendiously offered in order to inspect the legality or reliability of the analytical approach by judgment of numerical results.
Case study KIP 1-1
Case KIP 1-1 considers a wooden beam of one segment (Figure 19).
The properties are L = 3000 mm, L1 = 3000 mm, kbuc = 1, kbc =±1 Nmm,
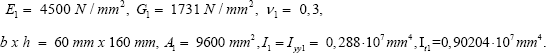
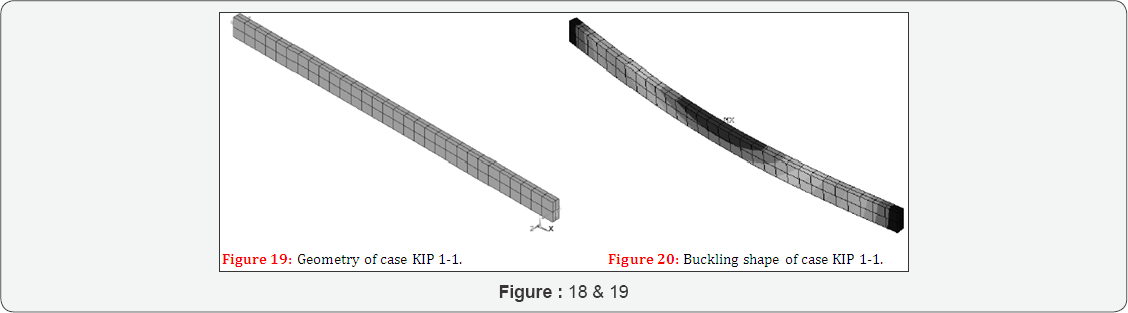
The results are M buaysanaiytcai = 0,149-108 Nmm and M buaysanaiytcai= 0,149-108 Nmm (Figure 20).
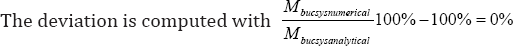
Case study KIP 1-2
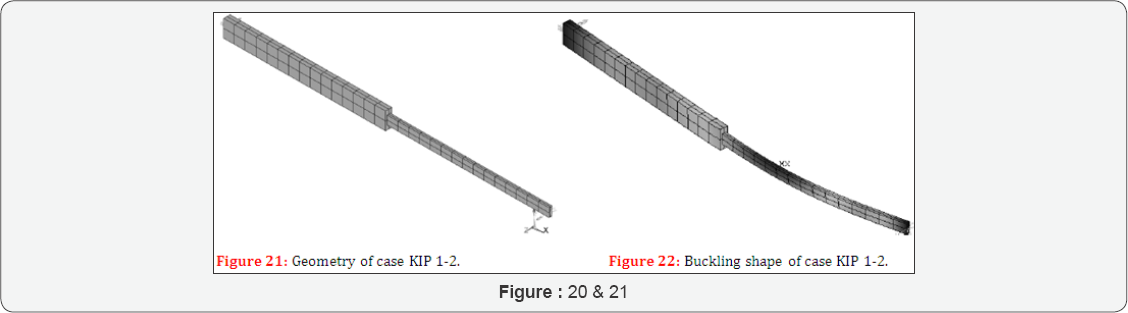
Case KIP 1-2 considers a composite wooden beam of two segments (Figure 21).
The properties are L = 3000 mm, L1 = 1500 mm, L2 = 1500 mm, kbuc = 1, kbc = 1, MZ = ±1 Nmm,
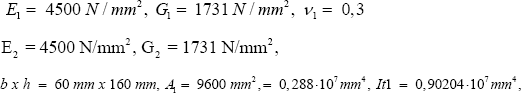
The results are M buaysanaiytcai = 0,175-107NmmM buaysanaiytcai and =0,176-107Nmm (Figure 22).

The deviation is +0, 57%.
Case study KIP 1-3
Case KIP 2-3 considers a composite wooden beam of three segments (Figure 23).
The properties are L = 3000 mm, L1 = 1000 mm, L2 = 1000 mm, L3 = 1000 mm, kbuc =1, kbc = 1, Mz = ±1 Nmm,
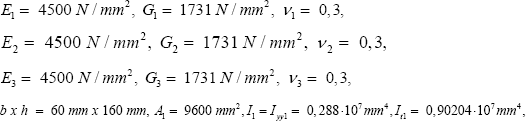
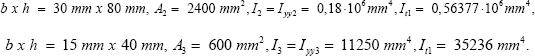
The results are M bucsysanalytical = 163701 Nmm and Mbucsysnumerical = 164801 Nmm (Figure 24).
The deviation is +0, 67 %.
Case study KIP 2-1
Case KIP 2-1 considers a steel beam of one segment (Figure 25).
The properties are L = 3000 mm, L1 = 3000 mm, kbuc = 1, kbc = 1, —z = ±1 Nmm,
The obtained results are M bucsysanalytical = 37, 48-106 Nmm and M bucsysanalytical = 37,5-106 Nmm (Figure 26).

The deviation is +0,053 %.
Case study KIP 2-2
Case KIP 2-2 considers a composite steel beam of two segments (Figure 27).
The properties are L = 3000 mm, L1 = 1500 mm, L2 = 1500 mm, kbuc = 1, kbc = 1, MZ = ±1 Nmm,
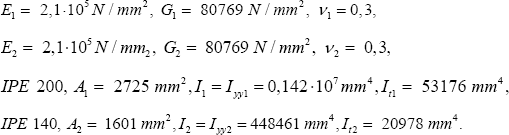
The results are M bucsysanalytical = 19, 55-106 Nmm and M bucsysanalytical= 19, 2106 Nmm (Figure 28).
The deviation is -1, 79 %.
Case study KIP 2-3
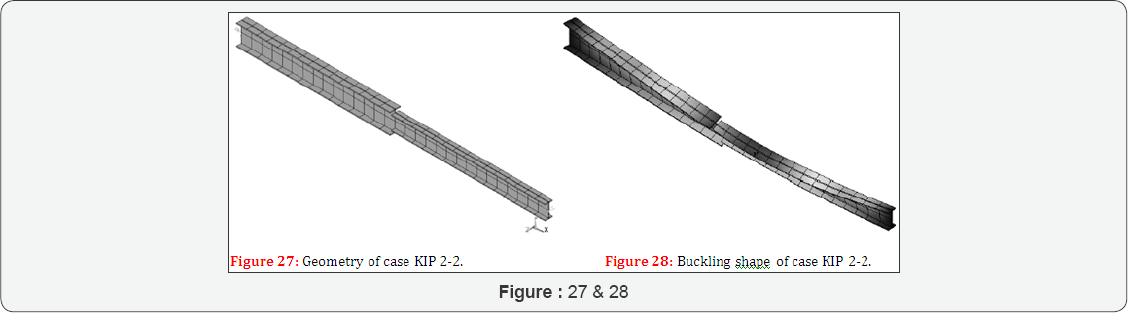
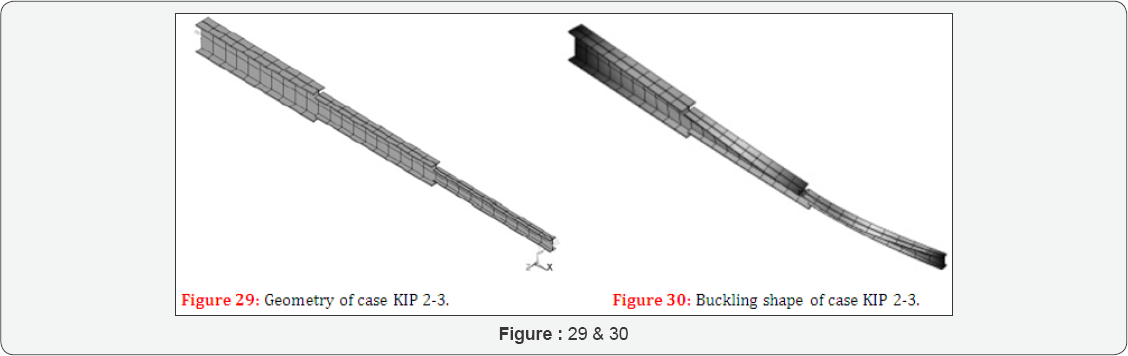
Case KIP 2-3 considers a composite steel beam of three segments (Figure 29).The properties are L = 3000 mm, L1 = 1000 mm, L2 = 1000 mm, L3 = 1000 mm, kbuc = 1, Kc = 1, MZ = ±1 Nmm,
The results are = 6, 91-106 Nmm are = 6, 68-106 Nmm (Figure 30).
The deviation is -3,328 %.
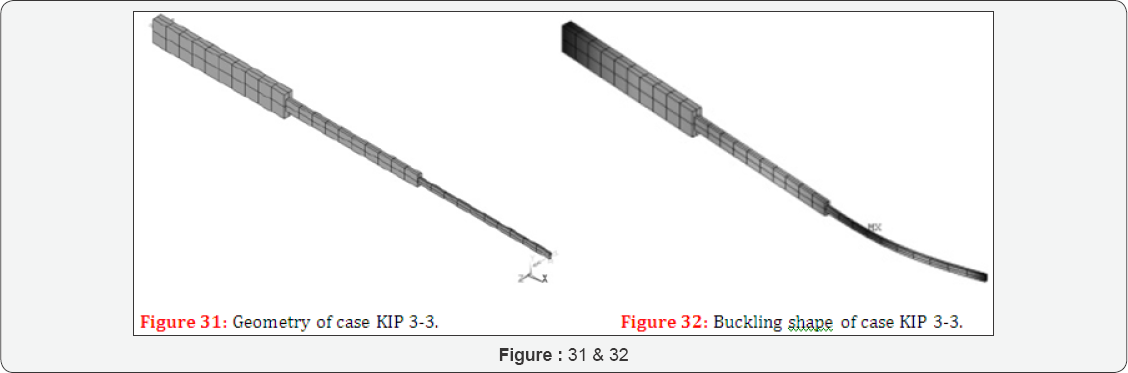
Case study KIP 3-3
Case KIP 3-3 considers a composite steel-wood beam of three segments (Figure 31).
The properties are L = 3000 mm, L1 = 1000 mm, L2 = 1000 mm, L3 = 1000 mm, kbuc = 1, kbuc = 1, MZ = ±1 Nmm,
The results are = 174324 Nmm and = 175756 Nmm (Figure 32).
The deviation is +0,821 %.
Conclusion
Numerical evaluation confirms the correctness of the presented linear elastic lateral shear and lateral torsional buckling analytical models. The deviations between the analytical and numerical approach are rather small and reveal clearly the ability to yield realistic outcomes. The supplied analytical linear elastic buckling models produce accurate and reliable values, which can be classified as suitable for engineering design purposes. Needless to cite that the analytical approach should always be cautiously applied and the results ought to be methodically checked by the responsible structural engineer. A salient observation is that the presented tactic could also be invoked for linear elastic buckling assessment of castellated and cellular (steel) beams. However, this assertion has not yet been verified and is thus speculative. Insertion of plasticity is straightforward however treatment of this topic is beyond the scope of this article.
References
- Det Norske Veritas (DNV) (2015) DNVGL-CG-0128, Class guideline - Buckling.
- Raven WJ (2006) Nieuwe blik op kip en knik, Stabiliteit en sterkte van staven. Dissertatie Technische Universiteit Delft.
- Van der Put TACM (2008) Discussion Elastic compressive-flexural- torsional buckling in structural members. HERON 53(3): 187-194.
- Tarnai T, Mc Graw-Hill (1995) Summation Theorems in Structural Stability.
- Timoshenko SP and Gere JM (Eds). Theory of Elastic Stability (2nd edn), 17th printing, Newyork 2017.
- Petersen C (2013) Steel construction Fundamentals of calculation and structural design of steel structures. (4th edn), Springer, Germany
- Hartsuijker C, Welleman JW (2007) Engineering Mechanics. Volume 2: Stresses, Strains, Displacements.
- Pilkey WD (2007) Analysis and Design of Elastic Beams: Computational Methods. John Wiley & Sons.
- Pilkey WD (2005) Formulas for Stress, Strain, and Structural Matrices. (2nd edn), John Wiley & Sons.
- Bathe KJ (2016) Finite Element Procedures. Bathe KJ and Watertown MA (2nd edn) fifth printing.
- Zienkiewicz OC, Taylor RL, Fox DD (2014) The Finite Element Method for Solid and Structural Mechanics. (7th edn), Butterworth-Heinemann.






























