Research Article

Using DEM to Simulate the Behavior of Masonry and Rammed Earth Structures

Tan Trung Bui¹*, Ali LIMAM²

Department of civil, University of Lyon, France

Submission: September 30, 2017; Published: January 05, 2018

*Corresponding author: Tan Trung Bui, University of Lyon, France, Email : [email protected]

How to cite this article: Tan T B, Ali L. Using DEM to Simulate the Behavior of Masonry and Rammed Earth Structures. Civil Eng Res J. 2018; 3(1): 555603. DOI: 10.19080/CERJ.2018.03.555603

Abstract

The present opinion paper gauges the efficiency of Discrete Element Method (DEM) to reproduce the behaviour of masonry structures and rammed earth walls submitted to in plane or membrane loading, and out of plane or bending loading cases. The efficiency of the DEM is estimated for all nonlinear behaviours, from cracks appearance and associated stress re distributions, cracks propagation, until the failure mechanism related to the ultimate load.

Keywords: Masonry ; Rammed earth ; Discrete element method

Introduction

Discrete element method (DEM) has its origin in the early 1970s. Initially used to simulate progressive rock movement using rigid block assemblies in two dimensions [1,2]. This technique was later extended to predict the mechanical behavior of masonry [3-5] and rammed earth structures [6]. In DEM, the heterogeneous nature of the masonry or rammed earth is taken into account explicitly, and the discontinuity of interfaces between blocks or earthen layers can be described. Masonry blocks or rammed earth blocks are represented as an assembly of rigid or deformable blocks which may take any arbitrary geometry. Rigid blocks do not change their geometry as a result of any applied loading. Deformable blocks are internally discretised into finite difference triangular zones. These zones are continuum elements as they occur in the finite element method (FEM). However, unlike FEM, in the distinct element method a compatible finite element mesh between the blocks and the joints is not required. Mortar joints or earthen layers are represented as zero thickness interfaces between the blocks. Representation of the contact between blocks is not based on joint elements, as for continuum finite element models. Instead, the contact is represented by a set of point contacts with no attempt to obtain a continuous stress distribution through the contact surface. The assignment of contacts allows the interface constitutive relations to be formulated in terms of the stresses and relative displacements across the joint. As with FEM, the unknowns are the nodal displacements and rotations of the blocks. However, unlike FEM, the unknowns in DEM are solved explicitly by differential equations from the known displacement while Newton's second law of motion gives the motion of the blocks resulting from known forces acting on them. So, large displacements and rotations of the blocks are allowed with the sequential contact detection and update of tasks automatically. This differs from FEM where the method is not readily capable of updating the contact size or creating new contacts. This method is also applicable for quasi-static problems using artificial viscous damping controlled by an adaptive algorithm. In view of the diversity and complexity of non-linear behavior observed across masonry and rammed earth structures, the validation of discrete modeling remains a crucial task.

Application of DEM

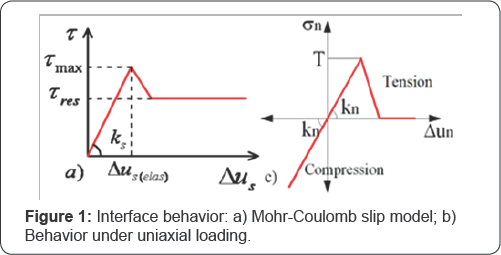
The 3DEC code (Itasca, 2011) can be used for DEM. The masonry or RE wall is modeled as an assemblage of discrete blocks (earthen layers), and the interfaces between earthen layers are modeled by introducing an interface law. The interfaces between blocks or earthen layers can be modeled by an interface law between the blocks following the Mohr-Coulomb interface model with a tension cut-off [6]. This interface constitutive model considers both shear and tensile failure, and interface dilation is included. In the elastic range, the behavior is governed by normal and shear stiffness of the interface (Figure 1).

For masonry structures, this simple interface behavior has been conducted in [5] to gauge the efficiency of DEM to reproduce nonlinear behaviour of masonry walls submitted to in plane or out of plane loads. The numerical simulations provide good agreement with experimental results (Figure 2). In particular, the conducted simulations allow us to qualify the bearing capacity of the structures as well as the associated failure modes. The nonlinear behaviours observed in the experimental load-deflection curves are globally correctly reproduced from the initiation up to the final failure. This, traduce that crack appearance and propagation, are correctly reproduced. Stress re distributions inherent to cracks, are also correctly managed, which permits to catch crack propagation and the final failure mechanism traducing the correct estimation of the bearing capacity as well as the characterization of the collapse mode of the structure.

For rammed earth structures, the study conducted by [6] showed that the DEM with the Mohr-Coulomb model reproduced the failure mode better than the FEM did (with Mazars' damage model) as shown in a previous study Bui et al. [5]. The results confirmed that, in the case of vertical loading, interfaces did not have an important effect on the behavior of RE walls. In the case of diagonal loading (which can simulate a seismic case), interfaces should be considered in order to produce better results relative to the ultimate load and failure modes (Figure 3).

Conclusion

In the conclusion, the DEM is relevant for the simulation of failure of masonry and rammed earth structures, where good quality results have been achieved. The discrete element method allows to simulate rupture phenomenon and thus to manage discontinuities in an elegant and robust way.

References

1. Cundall PA (1971) 'A computer model for simulating progressive, large scale movements in blocky rock systems”. Proc Int Symp Rock Fracture, ISRM, Nancy 1: 2-8.
2. Cundall PA (1971) The measurement and analysis of acceleration in rock slopes, Ph.D. Thesis, Imperial College of Science and Technology, University of London.
3. Lemos JV (2007) Discrete Element Modeling of Masonry Structures. International Journal of Architectural Heritage, 1: 190-213.
4. Bui TT, Limam A, Bui QB (2014) Characterization of vibration and damage in masonry structures: experimental and numerical analysis. European Journal of Environmental and Civil Engineering.
5. Bui TT, Limam A, Sarhosis V, Hjiaj M (2017) Discrete element modelling of the in-plane and out-of-plane behaviour of dry-joint masonry wall constructions. Engineering Structures 136: 277-229.
6. Bui TT, Bui QB, Limam A, Morel JC (2015) Modeling rammed earth wall using discrete element method. Continuum MechThermodyn 28(1-2): 523-38.