Open AccessJournals | List of Open Access Journals

Research Article

Evaluation of Canalization Slope on the Manning Roughness Modulus in Mountain Regions

Nasrin Shojae¹, Mahmood Shafaei-Bejestan², KavehOstad-Ali-Askari³* and Saeid Eslamian⁴Maryam Marani-Barzani, Masoud Kazem, Vijay P. Singh, Nicolas R. Dalezios, Mohsen Ghane

¹Department of Water Science Engineering, ShahidChamran University of Ahvaz, Iran

²Department of Water Structure, ShahidChamran University of Ahvaz, Iran

³Department of Civil Engineering, Islamic Azad University, Iran

⁴Department of Water Engineering, Isfahan University of Technology, Iran

⁵Department of Geography, University of Malaya (UM),50603 Kuala Lumpur, Malaysia.

⁶Civil Engineering Department, Najafabad Branch, Islamic Azad University, Iran.

⁷Department of Biological and Agricultural Engineering & Zachry Department of Civil Engineering, Texas A and M University, 321 Scoates Hall, 2117 TAMU, College Station, Texas 77843-2117, U.S.A.

⁸Laboratory of Hydrology, Department of Civil Engineering, University of Thessaly, Volos, Greece & Department of Natural Resources Development and Agricultural Engineering, Agricultural University of Athens, Athens, Greece.

⁹Department of Civil Engineering, South Tehran Branch, Islamic Azad University, Tehran, Iran.

Submission: July 12, 2017; Published: September 25, 2017

*Corresponding author: Dr.KavehOstad-Ali-Askari, Department of Civil Engineering, Islamic Azad University, University Blvd, Arqavanieh, Iran, Tel: +983135354001-9, Fax: +983135354060; Email: koa.askari@khuisf.ac.ir

How to cite this article: Nasrin S, Mahmood S B, KavehOstad A A, Saeid E. Assessment of Drainage Slope on the Manning Coarseness coefficient in Mountain Areas. Civil Eng Res J. 2017; 2(4): 555592. DOI: 10.19080/CERJ.2017.02.555592

Abstract

Determine the flow resistance parameters are important in hydraulic calculations of mountain area with steep slops. The purpose of this study is investigation the effect of slope, speed, depth and size of roughness on the manning roughness coefficient in this shallow stream region. This is an experimental study about manning roughness determined for mountain areas covered by particles in three different sizes and three gradients for different hydraulic conditions in a flume of 8.3m long, 0.8m width and 0.5m height under bed slope of 0.0005. At the end of flow changes against the Manning roughness coefficient are shown, which includes above hydraulic parameters and discussed.

Keywords: Shallow waters; Manning coefficient; Mountain areas

Introduction

Overall, for the calculated flow, velocity and depth of flow in natural channels, as estimates of flood and sediment flow resistance evaluation is important. Hydraulic resistance for open channels and surface flows on steep mountainous areas is an important feature to determine the characteristics of hydraulic flow for modeling runoff, routing flood, inundation and erosion is the most important. The resistance not only affects to estimate the flow variables such as depth and flow rate but also the results of these variables, such as flow distribution in the basin and sediment transport capacity are influenced. The resistance of a surface can be identified by the number of hydraulic roughness coefficient. The things that most used in this study are: Manning roughness coefficient (n), Chezy resistance factor (c) and Darcy- Weisbach resistance factor (f). In fact, estimates of these factors can help to estimate more accurate flow conditions.

Also in all numerical models that are used to estimate the flow conditions such as depth, velocity, shear stress and etc in rivers and open channels that used today, it is necessary to determine one of the three factors mentioned. The following relationships related to the calculation of these coefficients that expressed. The relationship between the mean flow velocity (V) and resistance coefficients, geometric and hydraulic surface:

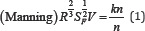
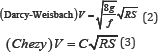
According to studies, Hill et al Darcy-Weisbach coefficient (f) use more strength formulations in experimental studies, but (n) coefficient is the best factor for hydraulic models. So in this study we will evaluate the effect of associate variables on the Manning roughness coefficient (n). Factors that affect the Manning roughness coefficient either decrease or increase in the strength of hydraulic indirectly affect the relationship are important. Different studies and analyzes indicators in this regard as well as experimental modeling and mathematical modeling, and they are looking for relationships between hydraulic properties of the flow in the hydraulic resistance in outdoor conditions, particularly the flow of the river Models has been done, but few studies have investigated about shallow stream in areas with steep slope. These study tried to appropriate relations by review a number of variables such as the Re number, the Fr number, the roughness characteristics (eg, with respect to the depth of roughness), Domain slope and vegetation cover ratio obtained in this area.

Most recent studies obtained experimentally relationships with application to shallow surface flows, channel pipes and smooth channels, also for turbulent flows obtained different relationships dependent on the toward. So far, many studies has been done on the impact of sediment particle size and the body surface during the Manning roughness coefficient (n) that Manning roughness coefficient (n) is only a function of the average particle size bed (Ks 1/6) was introduced such as Strickler studies , Mir Peter Mueller, CoilGun, Henderson, Anderson and colleagues and Hugger.

As well as lot of research has been done about the effects of vegetation on roughness coefficient both outside and inside the country in the field of plant-based (vegetation) coating roughness based Fathi-Moghadam research for non-submerged vegetation and cowen research according to Nikuradse theory of relative roughness's for vegetation submerged. Generally in order to select the correct Manning roughness coefficient (n) must be determined the factors that affect the (n) value. These factors include: surface and fuselage roughness, vegetation, irregular cross-section drainage, sedimentation and scour, barriers, water level and flow, suspended load and bed load. The exact calculation of the coefficient n by expert engineering is not possible, and depends on engineering judgment, so lack of detailed estimates Manning roughness coefficient (n) will reduce the efficiency of the project. Acquiring field information to determine the roughness coefficient is very difficult and takes too much time and cost. Therefore, in solving river engineering problems, in many cases used from empirical or semi-empirical or tables brigade. Roughness coefficient has an important role of flow rate, velocity, shear stressboundary and many other hydraulic parameters. So understanding this parameter is essential for optimal design of open channels and other channels.

Materials and Methods

In order to achieve the purposes of this study, several tests were conducted in the hydraulic laboratory Shahid Chamran University, Ahvaz, Iran. This laboratory has a main tank, that municipal water network be fed, and then tanks water transferred into the flume by pump through a pipe with a diameter of three hundred millimeter, then a split 63mm. The flume used in the experiments in this study has a length of 3.8 meters, width 80cm, depth 50cm and slope was 0.0005 that its structure has made of metal, which is generally from corners and walls made of Plexiglas with a thickness of ten mm for observation the flow behavior. After entering the flow in to the channel and adjust the rate by digital flow meter over a distance of approximately two meters flow arrives to the beginning of the ramp-arrow appears.

It should be mentioned the measurement of flow rate in this test by an electronic flow meter with precision three zero (thousand) liters per second was performed through sensors to split Sixty-three millimeter d related to incoming stream that connected to the flume. To slow the flow of water at the beginning of flume used from a square plate made from fiber size of 80* 80cm on the surface of the flow water. During slope that under three different roughness sizes and a smooth plate was tested in all experiments was constant and equal to 0.8cm. After passing the gradient surface with distances of 3.5 meters has the flow arrived to the end of the flume, and finally removed from valve terminal.

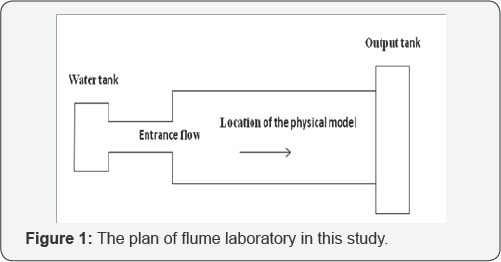
In Figure 1 channel plan (80cm), its equipment and the location of the sloping plane and in Figures 2 & 3 the way measure depth by point meter are shown. In this study, generally was used from three different slope and spicy (20, 30 and 35%). At each Were installed stage of the slope and a vertical adjustment for backrest to prevent entering water in to the bottom of a steep and long it by hydraulic pressure of water, that in terms of the physical form of the model is as a kind of vertical wedge. As well as on the corners between vertical plate and slope plate it's created a compact plastic tubing with a diameter of one centimeter to a climactic and the same conditions for water flow on slope and avoid break the flow of water was placed. It is noteworthy that all the perimeter of the wedge is sealed by adhesive aquarium to prevent the error discharge (flow rate).

First experiments related to the flat panel is done in different flow rate, then the steep panel dry and the desired roughness plane which surface roughness specified by siftings for each roughness size have been uniformly sized, and attached to form dense iron by adhesive on a plastic plate with a thickness of about three millimeter or less. Then, it has stabilized on the screen tilted by a drop of adhesive and aquarium in order to prevent it from moving flow and causing errors due to current passing flow rate between the slope and plastic screen under roughness. Then proceeded to turn on the pump and increase inflow discharge to entering the flume by the inlet valve. After ensuring that the desired flow rate and flow conditions is constant, level of water were measured in a square grid of sixteen points on the lateral and length by the depth point with a precision of one millimeter [1-11] (Figure 4-6).

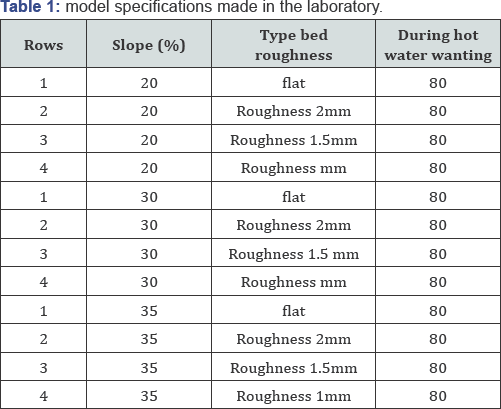
The remarkable thing is that measures are taken perpendicular to horizontal plane, but the slope calculation in each model was applied to the data. In this study the three types of aggregate with three different sizes were used as roughness. Tests were performed for each of the slope of 35, 30 and 20%, with five rate 0.8, 1.6, 2.4, 3.2 and 4 liters per second and three roughness in size 2,1.5and 1 millimeter that in the Table 1 given below:

Calculation

Considering that flow rate was constant and arbitrary in testing conditions, the flow rate unit on the width of 80cm in the flume set determined and also water level were measured longitudinally and transversely on sixteen points.

From average size of the elevation to get the flow rate based on the continuity relationship was used as follows:

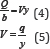
To achieve the effect of Manning roughness coefficients (n) Value of these parameters by variable parameters in the test from empirical formula Manning, according to data obtained from the test was used as follows:

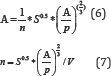
Results and Discussion

The aim of this study is essentially the effect of steep slopes in mountainous areas and the size of the roughness of the floor according to the rate specified on the Manning roughness coefficient. The variable factors measured included: The depth of the water flow at sixteen points for a network of longitudinal and Transverse Square. However, the three variable slopes, five variable rates, three variables size bed sediment and a flat surface were performed sixty and repeated three times for each test and we had one hundred and eighty tests sets.

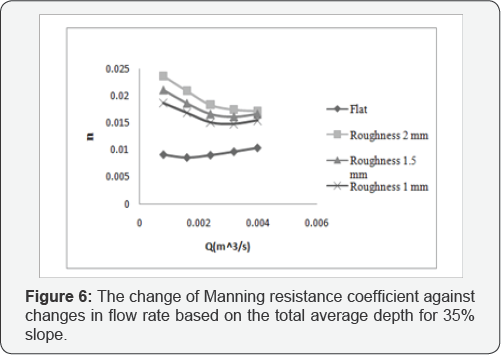
In the end the rate diagrams that include depth, speed, slope and roughness changes of the roughness coefficients were obtained as follows:

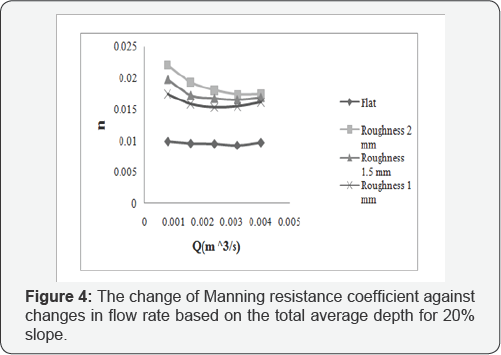
According to Strickler relationship the Manning roughness coefficient for n is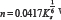 where Ks is the roughness height in meters, roughness to be 1/6 the size of the roughness has a direct the relationship. Also people like Henderson in 1966, C and Raju in 1976 and Hugger in 1999 also found empirical relationships, which represent the relationship between Manning roughness and particle size. In this study, as specified in the charts, the Manning roughness is increased by increasing the size of the roughness indicates a direct the relationship. Also according to Manning, Manning roughness has an inversely relationship with the speed. Also a direct relationship between the size of the flow and the flow velocity is established. Consequently, as can be seen in the graphs: by increasing the flow rate increased speed and reduced Manning roughness.

But with increasing flow rate observed the known flow rate that the different size of varies slope the amount of this reduction and the resulting difference in the Manning roughness coefficient decreased and provide to a roughly constant. Gradient table has a direct relation to the amount of roughness and in (35%) slope have the highest amount of roughness. The conclusion and recommendations essentially if only a shallow mountain flows as runoff from precipitation in these areas to consider, Substantial change to increase the Manning roughness coefficient and thus reduce the environmental degradation that is the important objectives cannot be enforced. But generally in steep mountainous areas of shallow rivers can be used rate control structures and by reducing flow and thus control the depth and speed on hydraulic resistance added. So reduce erosion rates, as a result of the amount of sediment transport and cause problems in downstream units also decreases.