Nonlinear Dynamic Response Analyses of Nuclear Containments
YL Mo*, J Sawab, CH Luu, S Roy, M Masud and TTC Hsu
Department of Civil and Environmental Engineering, University of Houston, USA
Submission: August 10, 2017; Published: September 22, 2017
*Corresponding author: YL Mo, Department of Civil and Environmental Engineering, University of Houston, USA, Tel: 8329297887; Email: yilungmo@central.uh.edu
How to cite this article: YL Mo, J Sawab, CH Luu, S Roy, M Masud, TTC Hsu. Nonlinear Dynamic Response Analyses of Nuclear Containments. Civil Eng Res J. 2017; 2(4): 555591. DOI: 10.19080/CERJ.2017.02.555591
Abstract
The shear strength of shell elements in nuclear containments strongly depends on the softening behavior of concrete struts in the principal compression direction due to principal tension in the perpendicular direction. In the past, the Cyclic Softened Membrane Model (CSMM) which incorporates the effect of concrete softening has been developed to accurately predict the response of wall-type structures subjected to seismic loading. Recently, a CSMM-based shell element was developed that extended the applicability of CSMM to shell-type structures. In this paper, a nonlinear dynamic response analyses of a 1/13th scale nuclear containment subjected to seismic margins and near-fault earthquakes are carried out using the Simulation of Concrete Structures Software developed at the University of Houston by using OpenSees as a platform. The time history of response acceleration, first yielding of reinforcement, ultimate state and the corresponding safety factors are critically examined by the analytical data. The input acceleration and response acceleration for both far-field and near-field earthquakes were compared. The far-field response acceleration was found to be higher than the response acceleration of near-field, which was attributed to near-field input accelerations having restricted frequency content in lower frequencies as compared to far-field input accelerations.
Keywords: Nonlinear; Dynamic; Nuclear containment; Shell; FEM; CSMM
Abbreviations: CSMM: Cyclic Softened Membrane Model; RC: Reinforced Concrete; FEM: Finite Element Method; SCS: Simulation of Concrete Structures
Introduction
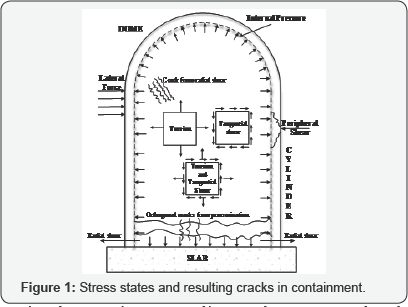
A nuclear containment vessel is a complex structure and needs significant safety requirements, such as pressure resistance, radiation leaking prevention, seismic and impact protection, etc. Considered to be a competitive material that satisfies the safety requirements of the containment structure, reinforced concrete has been used extensively from the beginning of the nuclear power industry. With the large dimensions of the structure, a reinforced concrete nuclear containment vessel often contains large sections and large diameter steel bars. The reinforced concrete nuclear containment vessel is classified as a shell-type structure with complex stress conditions, as shown in Figure 1, which involve various states. For example, internal pressure due to a leakage accident could produce large bi-axial tension, and an earthquake action could lead to seismic (tangential) shear, which has become a major design consideration. Airplane collisions, missile attacks, and other high local loads could lead to punching (peripheral) shear Banerjee & Holley [1].
The classical analysis of the shell structures includes two applied theories: the membrane theory and the bending theory Similar to plates, the shell structures can carry lateral loads by developing two bending moments and a twisting moment. The shell structures also can carry compressive and tensile loads in their plane by developing membrane actions Cook [2].
Compared to other types of shell structures, the structural behavior of RC shell structures is difficult to predict, especially when they are subjected to earthquake loading. The seismic response of RC shell structures is highly inelastic, which is caused by the highly nonlinear behavior of materials including the nonlinear constitutive relationships of reinforcement and concrete under reversed cyclic actions. However, from the structural point of view, a whole RC shell structure can be visualized as assemblies of many RC elements. This concept makes it easier to analyze this complex structure in which the finite element analysis combined with the proper constitutive models for concrete and reinforcing steel make it a powerful tool. The key to the rational analysis of the RC structure is to understand the behavior of one element isolated from the structure. Once a rational model is developed to predict the behavior of one element, this rational model can be incorporated into a finite element program to predict the behavior of the whole structure under different kinds of loading.
Because of the complexity of testing conditions, in an element-based study only a few research groups with special testing equipment could conduct an experimental study of shell elements. Two famous systems for testing RC shell elements are the Shear Rig developed by Vecchio & Collins [3] at the University of Toronto and the Universal Panel Tester developed by Hsu & Belarbi, et al. [4] at the University of Houston. Using the experimental results of the panel tests, many constitutive models for reinforced concrete have been proposed. The models are the Compression-Field Theory and Modified Compression Field Theory by Vecchio & Collins) [5], Vecchio & Collins [6]; Disturbed Stress Field Theory by Vecchio [7]; Rotating-Angle Softened Truss Model (RA-STM) Belarbi & Hsu [4], Pang & Hsu[9] , the Softened Membrane Model (SMM) Hsu & Zhu [10], and the Cyclic Softened Membrane Model (CSMM) Mansour & Hsu [11]. They all satisfy Navier's three principles of mechanics of materials and, thus, are rational. Among these constitutive models, the CSMM is the most versatile and accurate. The CSMM is capable of predicting the cyclic shear behavior of reinforced and prestressed concrete membrane elements including the stiffness, ultimate strength, descending branch, ductility, and energy dissipation.
Over the past decades, researchers at the University of Houston have made significant contributions to the finite element analysis of reinforced concrete elements and members subjected to shear. Using the OpenSees framework, they developed a two-dimensional (2D) reinforced concrete element, the RCPlaneStress Quadrilateral element, which is based on the CSMM. The UH researchers implemented the element into the Simulation of Concrete Structures (SCS), which is a nonlinear finite element computer program. SCS showed a significant capability of simulating the behavior of RC structures such as shear walls, bridges columns subjected to static, reversed cyclic, and dynamic loading.
Although the SCS program with RCPlaneStress Quadrilateral element based on the CSMM is capable of accurately predicting the behavior of concrete structures, it, however, cannot be used to model RC shell structures. Because the RC shell structures are three-dimensional (3D), problems with complex loading conditions while the RCPlaneStress Quadrilateral element can only be valid for 2D problems. Therefore, a new shell element based on CSMM was developed by Luu et al. [12] and implemented into the finite element program SCS-3D to predict the nonlinear behavior of RC shell-type structures. The research was conducted by a model-based simulation approach that included four steps: modeling, implementation, validation, and application. The CSMM-based shell element was developed by utilizing formulation of the degenerated shell theory with layered approach [13], and taking into account the Cyclic Softened Membrane Model (CSMM). The formulations of CSMM were extended from 2D to 3D so that they could be implemented into each layer of the shell element.
The capacity of the analytical models in predicting the behavior of RC shell structures using the developed CSMM- based shell element was verified by experimental data from several large-scale tests of RC shell structures subjected to monotonic, cyclic and seismic loadings. The structures selected for validations included a panel tested under pure shear Mansour & Hsu [14]; Pang & Hsu [15], panels tested under pure bending and combination of shear and bending Polak & Vecchio [16], a 3D RC cylindrical tank Maekawa, Okamura & Pimanmas [17], a RC shear wall, and six RC rectangular and circular hollow bridge piers Yeh & Mo [18]; Yeh, Mo, & Yang [19].
Furthermore, the developed CSMM-based shell element was applied to investigate the structural behavior of the reinforced concrete nuclear containment vessel under reversed cyclic loading. Two 1/13-scaled RCCV specimens were designed and tested at the National Center for Research on Earthquake Engineering (NCREE). The behaviors of the specimens were experimentally investigated. The nonlinear finite element analysis of the nuclear containment vessel specimens was conducted through the finite element program SCS-3D using the proposed CSMM-based shell element. The analytical model accurately predicted the behavior of the specimens including the cracking patterns, the first yielding points, yielding distributions of the steel bars, and the overall hysteretic loops of the load and displacement curve [29].
Under seismic loading, the nuclear containment vessel is subjected to cyclic flexural, axial and Shear forces. Shear behavior is an important consideration in a concrete containment wall, and a realistic assessment of shear strength and stiffness across cracks is essential to the design and analysis of concrete structures. Because of its critical importance to nuclear safety, the containment structure must be able to maintain structural integrity while undergoing simultaneous stresses of internal pressure, earthquake action, and/or high local loads. Under these conditions, the accurate assessment of shear behavior poses a difficult design and analysis problem Leombruni et al.[20]. Therefore, the SCS-3D finite element program is used to perform analyses of the 1/13-scale RCCV specimens under real seismic loadings.
Approach
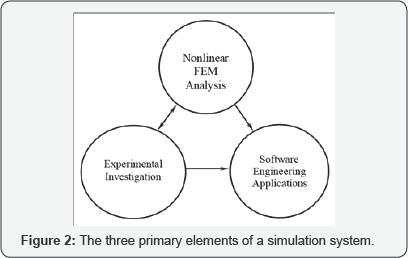
As the traditional approach such as analytical methods and experimental methods are and still will be essential, computer simulation has now become a third path to knowledge in many fields. Nonlinear FE method is certainly one of the most important approaches to computer simulation in structural engineering. Meanwhile, the best form of realization and representation of a simulation methodology may be its implementation as computer software. Thus, software engineering issues such as software reuse, component-based software development, and internet computing application to engineering software are also crucial for the simulation system to be successful. The relationships among these approaches are as depicted in Figure 2.
This research was conducted by a model-based simulation approach that included four steps: modeling, implementation, validation, and application. The National Science Foundation proposed an initiative called Model-Based Simulation (MBS), whose objective is to replicate the behavior of a complex system under loading and environmental condition. The core concept of MBS lies in the area of modeling (science), simulation (computing), and validation (experimentation) (Chen 2000), and is believed to be the future direction of structural engineering research.
According to Chen (2000), the development of model-based simulation for any civil engineering facility must involve the three steps: 1) mathematical modeling, 2) solution algorithm, and 3) software engineering. The contents of this research can be expressed in terms of the three steps:
a. Mathematical Modeling: Refined constitutive models of RC materials are studied and used to rationally account for the behavior of the materials subjected to reversed cyclic loads.
b. Solution Algorithm: Force-based non-linear fiber FE analysis is used to simulate the overall behavior of RC frame structures subjected to earthquake excitations. Artificial neural networks are employed to provide large-scaled quick estimation.
c. Software Engineering: An object-oriented programming framework is adopted to enhance software productivity, portability, and general quality, and a complete set of nonlinear FE software is developed.
Elements and Materials
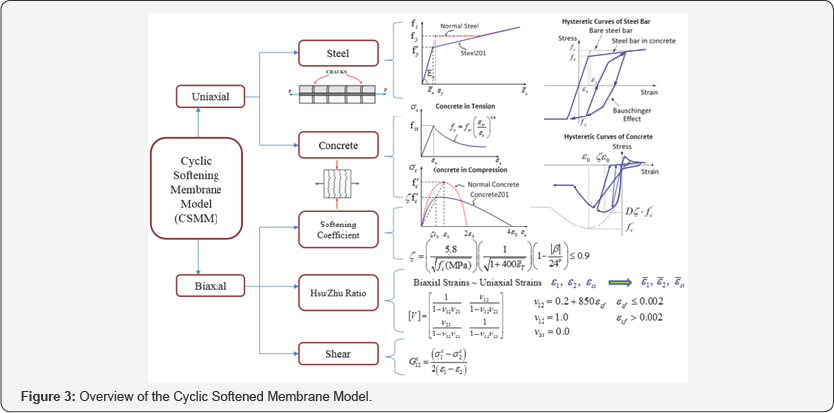
The constitutive model used is based on the Cyclic Softened Membrane Model proposed by Mansour & Hsu [21], as shown in Figure 3. The model is capable of accurately predicting the pinching effect, the shear ductility and the energy dissipation capacities of RC members. CSMM included the cyclic uniaxial constitutive relationships of concrete and embedded mild steel. The characteristics of these concrete constitutive laws include (1) the softening effect on the concrete in compression due to the tensile strain in the perpendicular direction; (2) the softening effect on the concrete in compression under reversed cyclic loading and (3) the opening and closing of cracks, which are taken into account in the unloading and reloading stages. The characteristics of embedded mild steel bars include (1) the smeared yield stress is lower than the yield stress of bare steel bars and the hardening ratio of steel bars after yielding is calculated from the steel ratio, steel strength and concrete strength and (2) the unloading and reloading stress-strain curves of embedded steel bars take into account the Bauschinger effect.
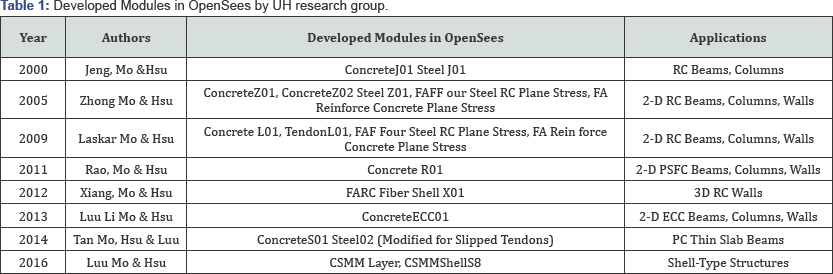
Zhong [22] formulated a two-dimensional reinforced concrete plane stress membrane element based on the Cyclic Softened Membrane Model to simulate the behavior of reinforced concrete shear walls subjected to static, reversed cyclic and dynamic loading. Recently, luu et al. [12] implemented a new shell element, the so-called CSMM-based shell element, into the SCS program. The element was developed based on the Cyclic Softened Membrane Model Mansour & Hsu [21] and the formulation of an 8-node Serendipity curved shell element Ahmad, Irons et al. [24] with a layered approach Scordelis & Chan [25]. A summary of the material models and elements that are developed by researchers at the University of Houston and implemented in OpenSees is shown in Table 1.
Implementation
Many available commercial finite element programs are available for the nonlinear analysis of shell structures, i.e. ABAQUS, ANSYS, ADINA, etc. However, not many of them have good constitutive models for reinforced concrete, especially models that can account for shear failure. These commercial programs usually are not open-source and, thus, put limitations on users in developing their material constitutive models. In recent years, the Pacific Earthquake Engineering Research (PEER) Center at the University of California, Berkeley developed an open/free finite element framework using object-oriented languages (C++), OpenSees (Open System for Earthquake Engineering Simulation) OpenSees [26]. OpenSees is an object- oriented framework for simulation applications in earthquake engineering using finite element methods. Key features of OpenSees include the interchangeability of components and the ability to integrate existing libraries and new components into the framework without the need to change the existing code. These features make it convenient to implement new classes of elements, materials, and other components.
Under the OpenSees framework, each finite element analysis consists of four main types of objects: Model Builder object,Domain object, Analysis object, and Recorder object, as shown in Figure 4.
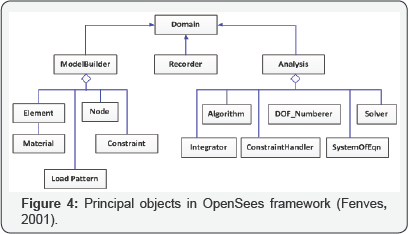
Under this framework, if a new type of element or new material is to be introduced, a new corresponding class of objects can be added to the OpenSees according to the designated specification of the framework without changing the existing code. This is because of the interface, which is defined in the core components (abstract classes), is minimal to make adding new component classes easier but large enough to ensure that everything is required can be accommodated (Fenves, 2005).

Over the past decades, researchers at the University of Houston have made significant contributions to the finite element analysis of RC elements and members subjected to shear. Using the OpenSees framework, the Cyclic Softened Membrane Model was implemented, and Zhong [22] developed a nonlinear finite element computer program, the Simulation of Concrete Structures (SCS). A 2D reinforced concrete plane stress material module, the RCPlaneStress, and three uniaxial material modules of concrete and steel, ConcreteZ01, ConcreteZ02, and SteelZ01, were first implemented into SCS program, as shown in Figure 5. SCS became a powerful FE tool to simulate the behavior of reinforced concrete elements/members/structures subjected to static, reversed cyclic, and dynamic loading.
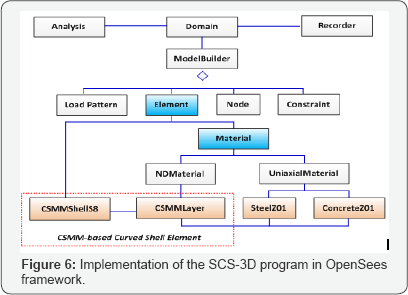
Recently, Luu & Mo et al. [12] implemented a new shell element, the so-called CSMM-based shell element, into the SCS program. The element module CSMMShellS8 represents the CSMM-based shell element. The nDMaterial module CSMM Layer was created to incorporate the formulation of the tangential material matrix for concrete and steel into each layer of the developed shell element as shown in Figure 6. The CSMMLayer was connected with the two uniaxial Material modules, SteelZ01 and ConcreteZ01, to determine the material constitutive matrix and calculate the stress of the elements at each layer. Two uniaxial Material modules for concrete (ConcreteZ01) and steel (SteelZ01) were created previously based on the uniaxial constitutive relationship of concrete and steel in CSMM Zhong [22].
Validation
The developed nonlinear finite element program SCS is verified by the experimental data in the literature Gao [27]; MA & Zhong [28]. Three types of structures, including framed shear walls subjected to axial load and reversed cyclic loading, Low-rise shear walls subjected to seismic loading, and nuclear containment subjected to reversed cyclic loading, are analyzed.

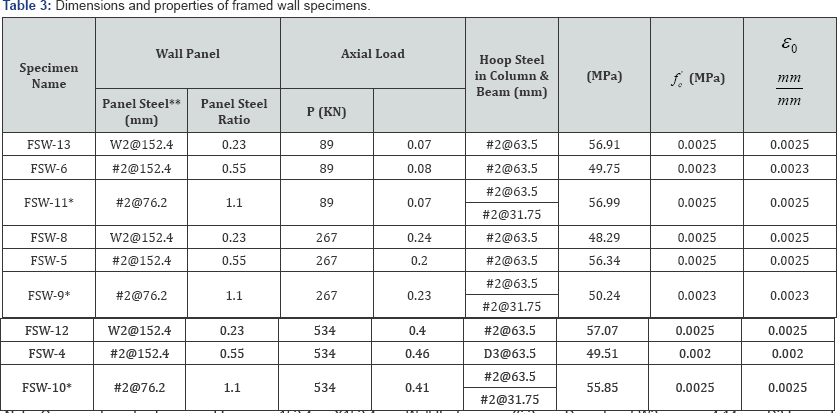
Note: Cross section of columnS and beams is 'lb2.4mmX152.4mm. Wall thickness is 76.2mm. Diameter of W2 wires is 4.14mm. D3 bar and' #2 bar have an approximately the same yielding strength of 14 KN. Longitudinal steel in columns and beams is 6#4 with longitudinal steel percentage of 3.33%. , A is the total area of the cross section of column and beams.
1MPa=14bPsi, 1Kips=4.448KN, 1inch=2b.4 mm.
*The three specimens with asterisks have seismic hoops (31.7bmm. spacing) in the potential plastic-hinge regions.
** Panel steel in both the vertical and the horizontal directions.
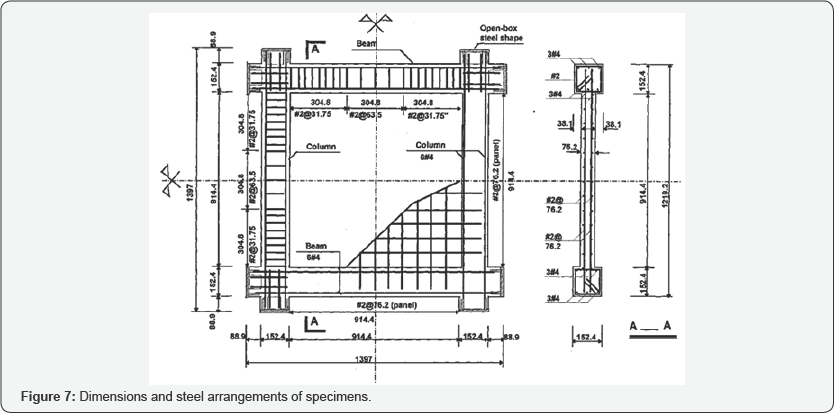
Framed shear walls subjected to reverse cyclic loading:A complete test program of nine shear walls tested by was analyzed using the developed program. Tests on nine 1/3-scale framed shear walls, subjected to a constant axial load at the top of each column and a reversed cyclic load at the top beam, were performed at the University of Houston. The wall dimensions were 914.4mm by 914.4mm with a thickness of 76.2mm. The cross-section of the boundary columns was 152.4mm square. Figure 4 demonstrates the details of dimensions and reinforcement of the specimens. The bottom left and right corners of the specimen were supported by a hinge and a roller, respectively. The test program includes nine specimens to study two variables as shown in Table 2. The first variable is the axial load ratios on the columns (P/Po): 0.07, 0.2 and 0.4. The second variable is the steel ratio in the wall panel which varied from 0.25% to 0.55% to 1.1%. The actual wall steel ratio and axial load ratio of each specimen are listed in (Table 3) (Figure 7).
Figure 8 shows the finite element mesh of the specimens. The wall panel was modeled as nine Quadrilateral elements with RCPlaneStress material. The steel ratio and the steel grid orientations of the wall panel were defined in the RCPlaneStress material. SteelZ01 and ConcreteZ01 were used to create the uniaxial constitutive laws of steel and concrete, respectively.
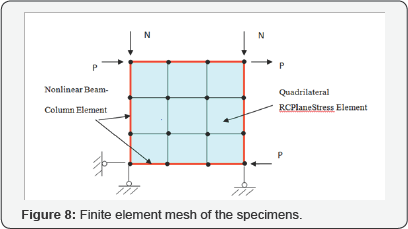
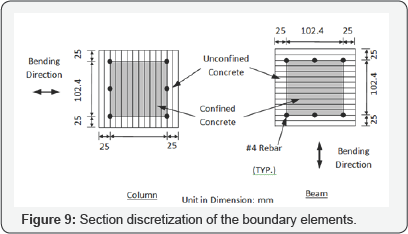
The present library of OpenSees has the fiber element named Nonlinear Beam Column capable of modeling the RC beams and columns. In this finite element mesh, each of the boundary beams and columns was modeled as three Nonlinear Beam Column elements. Each fiber elements were defined with 3 control sections. Figure 9 gives the configuration of the section discretization.
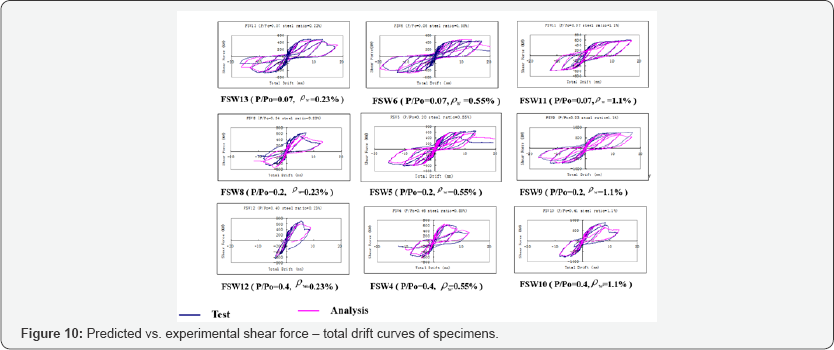
The analytical results of the sheer force-drift relationships of nine shear walls are illustrated by the solid purple curves in Figure 10. For easy comparison, the corresponding experimental results, indicated by the solid blue curves, are also plotted in the figures. It can be seen from the comparison that for the primary curves (backbone curves) the predicted outcomes agree very well with the experimental results in the initial stiffness, yield point, and ultimate state for all the specimens.
Low-rise shear walls subjected to seismic loading: Four low-rise shear walls with a height-to-width ratio of 0.5 were tested on a shake table. The specimens were designed with a scale factor of 1:2 according to the capacity limit of the shake table. Four specimens had the same dimensions of 700mm in height, 1400mm in length, and 60mm in thickness.
The four specimens were identified as ST1, ST2, ST3, and ST4, respectively. The labels of all specimens begin with the letters "ST," signifying that the specimens were tested on a shake table subjected to a seismic excitation. The variables in the test program were:
a. Concrete strength.
b. Boundary elements and
c. Steel grid orientation in the wall panel.
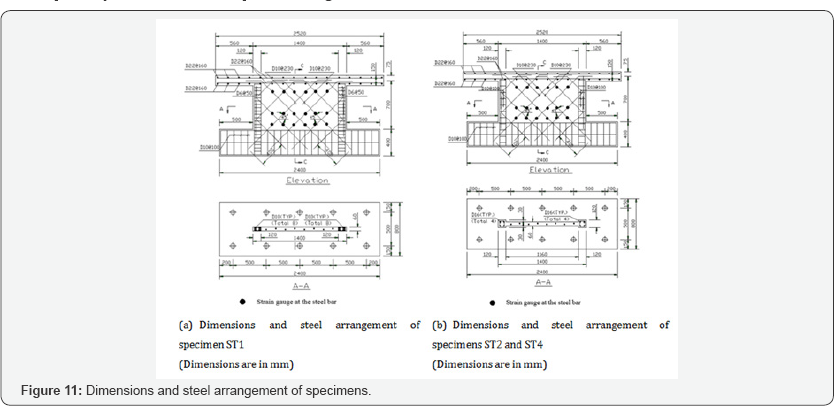
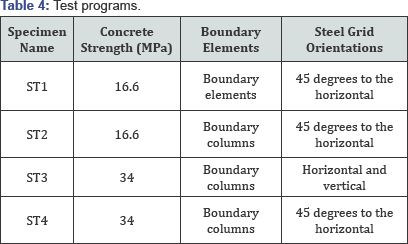
Details of the four specimens are listed in Table 4, wherein the test parameters are indicated. The dimensions and steel arrangements of the four specimens are shown in Figure 11.
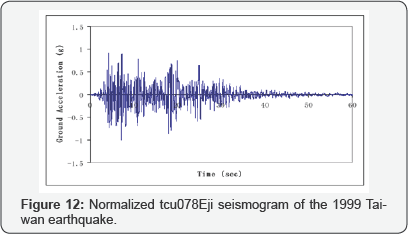
The tcu078Eji seismogram of the 1999 Taiwan earthquake was used as the ground motion acceleration for the shake table. The normalized seismogram is shown in Figure 6. In each test run, a scale factor was applied to the input ground motion acceleration such that the Peak Ground Acceleration (PGA) would reach the predetermined value Figure 12.
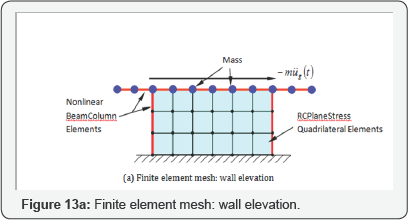
Nonlinear dynamic analyses were conducted on the four specimens using the proposed nonlinear finite element program SRCS. As illustrated in Figure 13a, the finite element mesh of the structure was divided into three zones: the web panel, the boundary elements, and the top slab. The wall panel was modeled using 18 RCPlaneStress quadrilateral elements. Each of the two boundary elements was modeled using 3 Nonlinear Beam Column elements, and the top slab was modeled using 8 Nonlinear Beam Column elements.
Only one type of RCPlaneStress Quadrilateral element was defined in the finite element model of each specimen, because the steel grid orientations and spacing were the same in the wall panel, and the material properties could be assumed to be uniformly distributed. According to steel grid orientations in the four specimens, the steel grid orientations in the RCPlaneStress Quadrilateral elements of specimen ST1, ST2 and ST4 were defined at 45 degrees and 135 degrees with respect to the horizontal direction. The steel grid orientations in the RCPlaneStress Quadrilateral element of specimen ST3 was defined in the horizontal and vertical directions. Uniaxial material modules SteelZ01 and ConcreteZ01 were used to create the constitutive laws of uniaxial steel and concrete and to relate them to the reinforced concrete material RCPlaneStress.
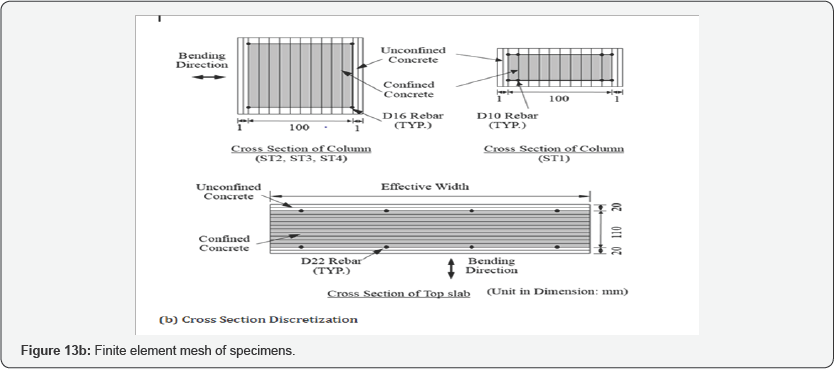
The boundary element at each side of the wall was modeled using 3 NonlinearBeamColumn elements. Each Nonlinear Beam Column element was defined with 3 control sections. As shown in Figure 13b, the white cells represent the unconfined concrete fibers, the gray cells represent the confined concrete fibers, and the black cells represent the reinforcing steel fibers. Concrete01 was used to define the concrete fibers in the cross section. The stress and strain of the confined concrete was determined based on the modified Kent and Park model. SteelZ01 was used to define the steel fibers in the cross section.
The calculated response time history of the four specimens at the test runs of elastic, steel yielding, and post yielding states are compared with the measured response time history.
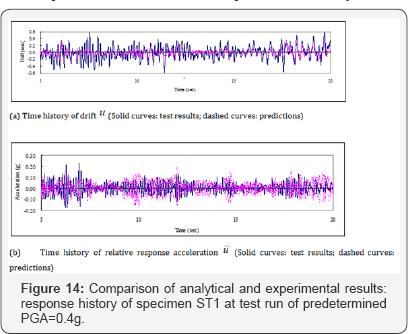
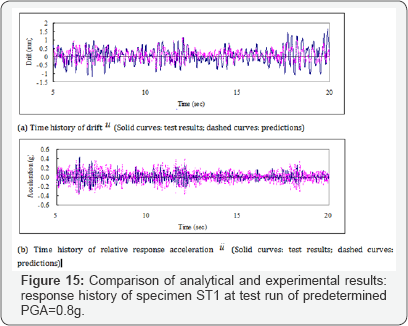
Only specimen ST1 will be discussed here to avoid repetition. The details of other specimens can be found out from the research paper by MA et al. [28]. For specimen ST1, the time history of the predicted drift and relative response acceleration for test runs with a PGA of 0.4g, 0.8g and 1.2g are compared with the experimental results in (Figures 14-16) respectively. The comparisons are presented in the first 20 seconds where the response of displacement and acceleration reached the most significant values in the entire time history.
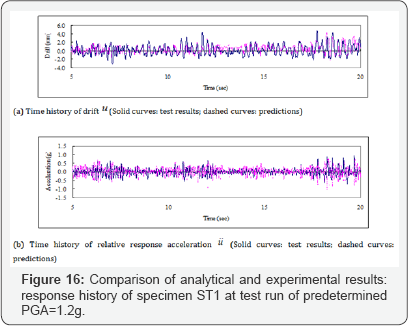
The calculated time history of drift and relative acceleration of the four shear walls agree well with the experimental curves in the test runs of the elastic stage, the steel yielding stage, and the post-yielding stage. The good agreement validates the nonlinear dynamic analysis capability of the proposed finite element program SRCS.
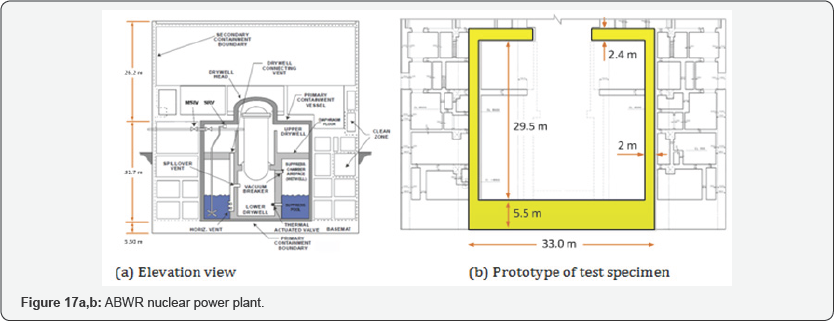
Nuclear containment structure subjected to reversed cyclic loading: The experimental program included the construction and testing of two 1/13-scale nuclear containment specimens. These specimens were designed to investigate the behavior of an RC nuclear containment isolated from a nuclear power plant and subjected to the gravity and earthquake loads. The specimens were designed based on the prototype of an Advanced Boiling Water Reactor (ABWR) nuclear containment structure (Figure 17a). The real-size containment has a height of 29.5m, a radius of 15.5m (center-line dimension) and a thick wall of 2.0m (Figure 17b). Each specimen included three parts: the main containment, top block and bottom block. The bottom block simulated the rigid foundation while the top block simulated the rigid floor system. These blocks were designed with steel plate boxes filled with concrete and a large amount of reinforcing steel. These blocks were designed conservatively to avoid significant deformation occurring in the blocks so that the nonlinearity occurred only in the containment walls during the tests. Rotations of the top and bottom blocks in the vertical plane were prevented during the test to ensure the containments deforming in a double-curvature manner during the tests. The dimensions of the test specimens are shown in Figure 18. The containments had a height of 2.25 m and a radius of 1.175m (centerline dimension). The outer and inner diameters of the containments were 2.5 m and 2.2 m, respectively. The thickness of the containment was 0.15m. The top and bottom blocks of the specimens had a cross section of 3.5m x 3.5 m and a depth of 0.73m.
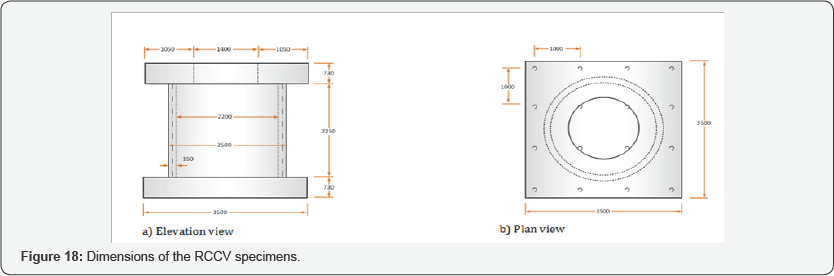
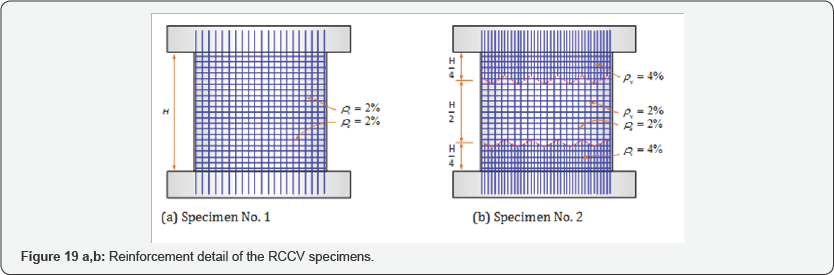
The reinforcement arrangement in the specimens is illustrated in Figure 19. Four layers of vertical and horizontal steel rebars were uniformly placed along the thickness of the containments. The steel rebars were uniformly distributed around the perimeter and along the height of the test containments with the same spacing. The percentage of the reinforcement ratio in the containment of Specimen No. 1 was 2% in both the vertical and horizontal directions (Figure 19a). The reinforcement arrangement of Specimen No. 2 was almost identical to Specimen No. 1 except that more vertical steel rebars (dowel bars) were added to each end of the containment to enhance its shear sliding capacity, resulting in the vertical reinforcement ratio of 4% in each of these two ends (Figure 19b). The cut-off points of the additional vertical steel rebars were arranged in a jagged manner to prevent cracking within the cutoff regions. The centerline of the zigzag curve was at a quarter of the containment height. The vertical bars in the containments were continuous without lap splices. The clear concrete cover over the vertical bars was 17mm. The details of dimensions and material properties of the specimens are summarized in Table 5. The compressive strengths of concrete of Specimen No. 1 and Specimen No. 2 at the testing date were 37.0 MPa and 43.3 MPa, respectively. Both specimens used the same steel bars taken from the same batch. The yielding strength of the vertical and horizontal steel bars was 379 MPa and 376 MPa, respectively.
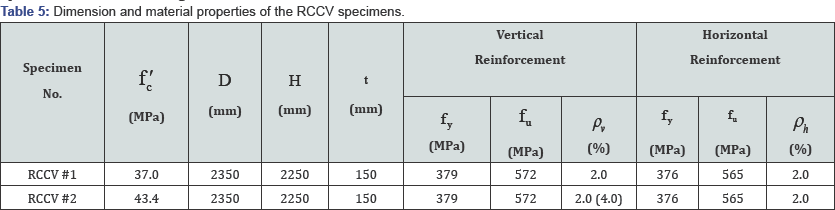
Note: = Compressive strength of concrete; = Diameter (Center-to-center); = Thickness; = Net height; = Yielding strength of steel; = Ultimate strength of steel; = Steel ratio in vertical direction; = Steel ratio in horizontal direction.

At the NCREE Laboratory in Taiwan, the test specimens were subjected to horizontal loading up to their maximum capacity with a set of specially built steel loading frames. The test setup was used to simulate gravity and the lateral and vertical earthquake loads. Figure 20 gives an overview of the test setup with various equipment components, including the horizontal actuators, vertical actuators, L-shape steel loading frame systems and the specimen. The specimens were loaded axially using four 1000-kN-capacity vertical hydraulic actuators. Pin connections were used at the end of the vertical actuators. The simulated lateral earthquake load was applied by eight 1000-kN-capacity horizontal actuators under displacement control. The horizontal actuators were bolted to a rigid concrete reaction wall and the L-shape loading frame so that the center of the loading axis passed through the specimen's mid-height. The specimens were connected to the strong concrete floor using high-strength all-thread steel rods that went through the foundation of the specimens. The loading frame was allowed to move freely in the vertical plane. Additional steel frames bolted to the solid floor were placed on the north and south sides of the specimen to prevent the horizontal out-of-plane displacement. During the tests, the containment specimens were subjected to constant vertical axial loads and horizontal reversed-cyclic load until failure.
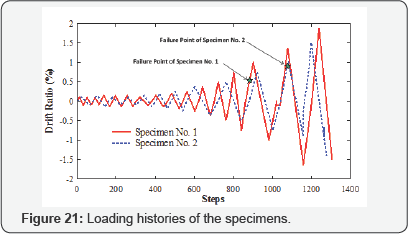
The first step of the loading protocol program was to apply an axial load that would remain constant during the test. The total initial vertical load equaled 1.6% of the axial concrete capacity ( ) of each specimen, where is the compressive strength of concrete and is the nominal area of the specimen. The axial concrete capacity was dependent on the compressive strength of the concrete; consequently, the total initial vertical load varied for each specimen. After the axial load had been applied, a reversed-cyclic load was added by the eight horizontal actuators under drift ratio control. First, the test specimens were subjected to several cycles of small drift ratios for warming up. Then, the tests were performed by using the loading history consisting of the following drift ratio cycles: 0.1%, 0.15%, 0.25%, 0.37%, 0.5%, 0.75%, 1.0%, 1.5%, and 2.0% (Figure 21).
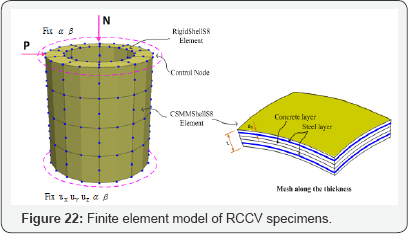
Analytical Model: The specimens were modeled using the finite element mesh illustrated in Figure 22. For each specimen, the cylindrical wall of the vessel was defined by 40 CSMM- based shell elements. The steel layers were defined at the exact locations of the steel in the cross section of the specimen. In Specimen No. 1, all shell elements were assigned with 2% of reinforcement in both the vertical and horizontal directions. The percentage of steel used in shell elements of Specimen No. 2 was almost identical to Specimen No. 1, except the shell elements located within the distance of one-fourth of the net height at the top and bottom of the specimen were assigned with 4% of vertical reinforcement. The top block of each RCCV specimen was defined as a rigid body by using ten 8-node linear-elastic shell elements with high stiffness. For the boundary conditions, all nodes at the bottom of the model were constrained to prevent any translations or rotations. Equal horizontal and vertical loads were applied at all nodes along the perimeter at the height level of the specimen based on the assumption that the loads were uniformly distributed. The axial loads acting on the cap were applied with the direction and magnitude of the loads remaining constant in the analysis. The horizontal loads were changed according to the displacement control scheme.
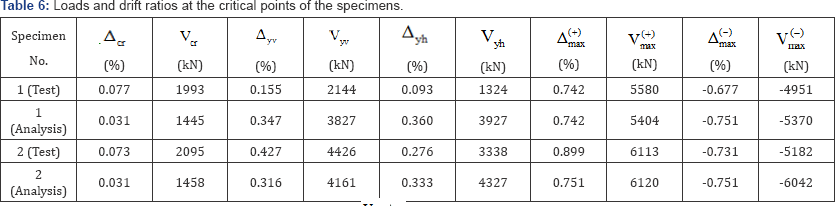
Note: Vcr,Δcr= Horizontal load and drift ratio at first cracking; Vyv,Δyv= Horizontal load and drift ratio at first yielding of vertical rebar; 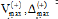 =Horizontal load and drift ratio at first yielding of horizontal rebar; ,
=Horizontal load and drift ratio at first yielding of horizontal rebar; , 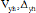 = Horizontal load and drift ratio at peak load in the positive direction;
= Horizontal load and drift ratio at peak load in the positive direction;
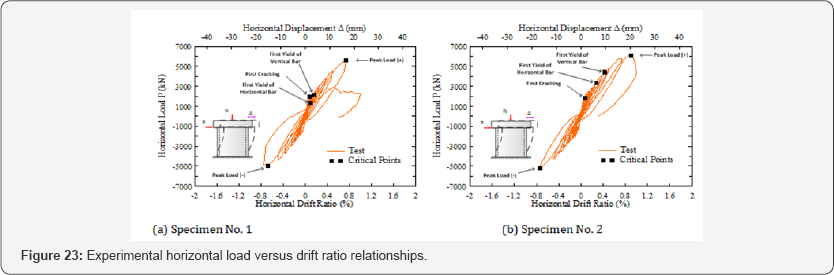
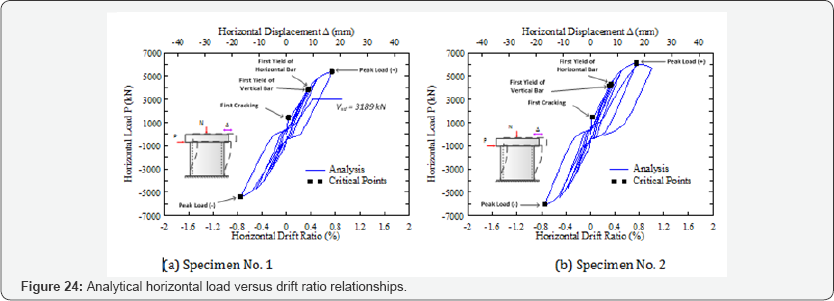
The experimental and analytical horizontal load versus drift ratio relationships of the test specimens are shown in Figure 23 and Figure 24, respectively. These curves illustrate the load resisting mechanism of the nuclear containment vessels. Five critical points were indicated in the horizontal load versus drift ratio curve representing the first cracking of concrete (Point 1), the first yielding of vertical and horizontal steel bars (Point 2 and Point 3) and the peak loads in the positive and negative directions (Point 4 and Point 5) in each specimen. The values of the load and drift ratio at the critical points of the specimens are summarized in Table 6. Overall, the analytical results had a good correlation with the experimental data. The analytical model accurately predicted the structural behaviors in both the positive and negative directions, including the primary backbone curve, the first cracking, the initial stiffness, the yielding distribution of steel bars, and the unloading and reloading paths as well as the pinching effect of the specimens.
The nonlinear finite element analysis of the nuclear containment vessel specimens was conducted through the finite element program SCS using the developed CSMM-based shell element. The analytically predicted results compared very well with the experimental data. Overall, the primary backbone curves, the initial stiffness, the peak strength, the descending branch, the yielding distributions and the failure characteristics were accurately predicted. The analytical hysteresis loops also provided accurate measurements of the pinching effect, and the energy dissipation capacity.
Nonlinear Dynamic Response Analyses of Nuclear Containments
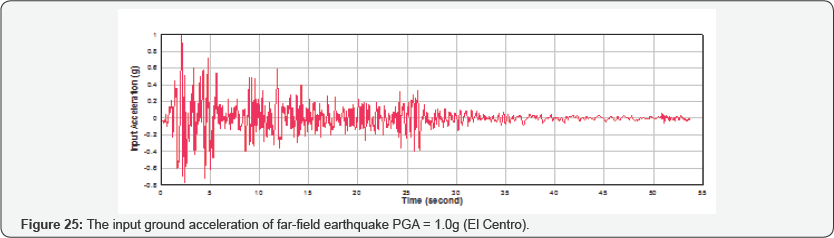
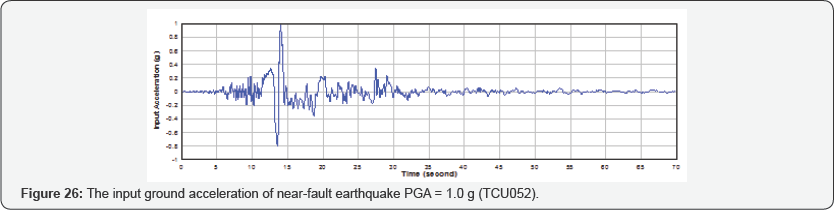
The Simulation of Concrete Structures program was used to perform a nonlinear dynamic response analyses on the 1/13th scale nuclear containment vessel. The specimen details and dimensions are described in Section 5.3. The analyses of the nuclear containment specimen are carried out with two types of earthquake excitations: The El Centro earthquake time history for far-field seismic analyses and The TCU052 earthquake time history for near-field seismic analyses. The normalized input ground acceleration for both the earthquakes is shown in Figures 25 & 26.
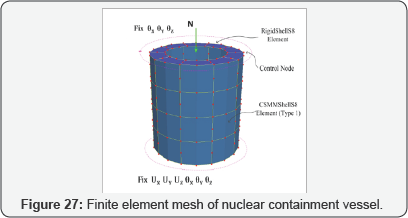
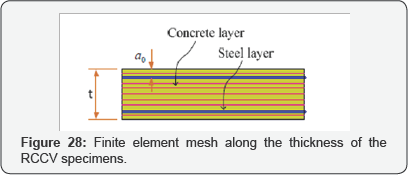
Analytical Model: The specimens were modeled using the finite element mesh illustrated in Figure 27. The cylindrical wall of the vessel was defnied by 40 CSMM-based shell elements. For the boundary conditions, all nodes at the bottom of the model were constrained to prevent any translations or rotations. Ten layers of concrete and two layers of steel were assigned for each element using the CSMM Layer material module, as shown in Figure 28. The steel layers were defined at the exact locations of the steel within the cross section of the specimen. All shell elements in the specimen are assigned with 1% of reinforcement in both vertical and circumferential directions.
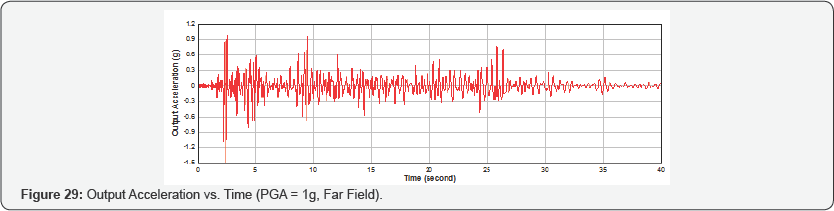
Far Field Seismic Analysis: The El Centro earthquake time history is selected as input earthquake excitation for far field seismic analysis of the nuclear containment specimen. In Phase 1, using one g as the peak ground acceleration, the mass (m) is increased to achieve the ultimate state (i.e. when the compressive strain of the concrete reaches 0.003). The response acceleration of the nuclear containment is shown in Figure 29. The input ground acceleration and output response acceleration are compared in Figure 30.

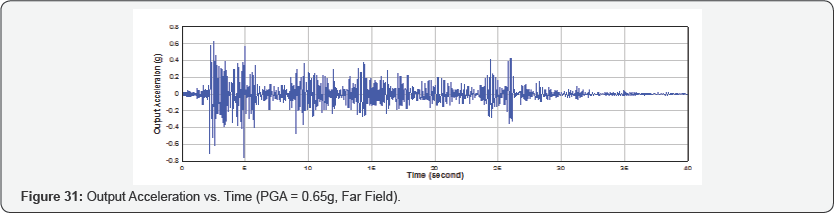
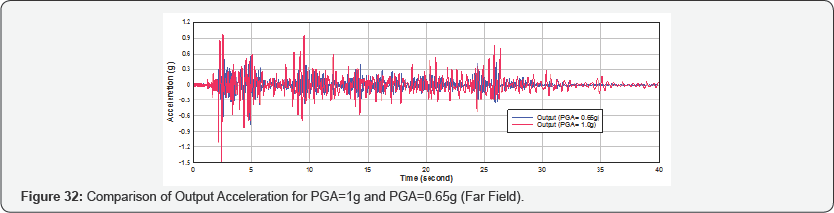
In Phase 2, the mass obtained from the ultimate state is kept constant and the peak ground acceleration (PGA) of the input earthquake excitation is decreased to obtain the first yielding behavior. From the far field seismic analysis, it is predicted that the ultimate state is achieved when the mass is increased to the 5.5 times of its initial mass at a PGA of 1.0g and the first yielding state is achieved at a PGA of 0.65g. The output acceleration for 0.65g PGA is shown in Figure 31. The response acceleration for yielding state and ultimate state is compared in Figure 32. The seismic margin can be calculated as the ratio of the PGA at the ultimate state to the PGA at the first yielding state. From the far field, seismic analysis of nuclear containment specimen, the seismic margin is calculated as 1.54.
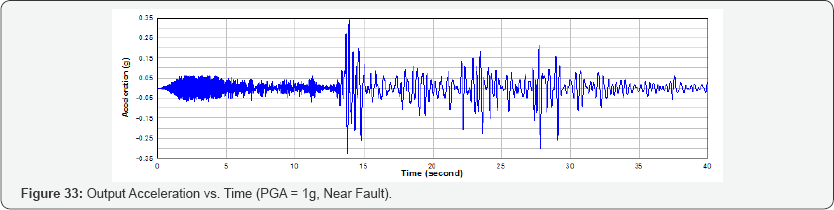
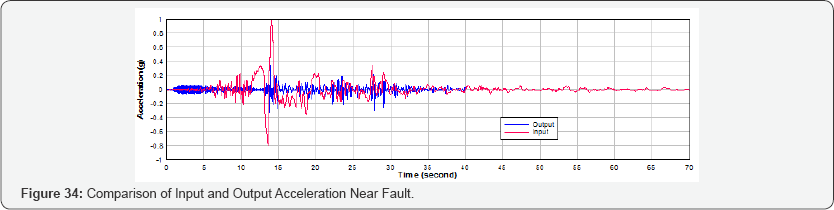
Near Fault Seismic Analysis: For the near fault seismic analysis, TCU052 earthquake time history is selected as the input earthquake excitation to the nuclear containment specimen. In Phase 1, the mass (m) is increased to achieve the ultimate state (i.e. when the compressive strain of the concrete is 0.003). The response acceleration of the nuclear containment is shown in Figure 33. The input ground acceleration and output response acceleration are compared in Figure 34.
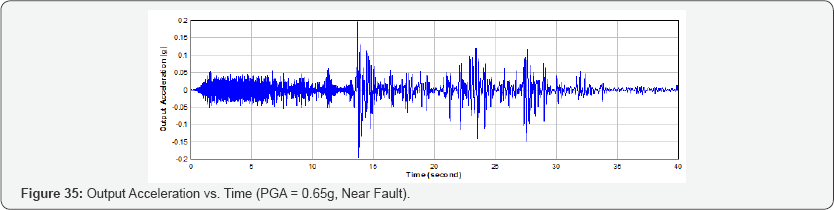
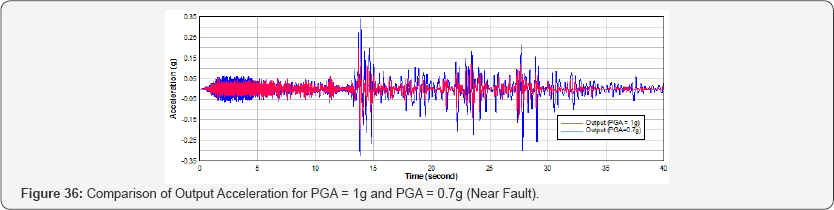
In Phase 2, the mass obtained from the ultimate state is kept constant and the peak ground acceleration of the input earthquake excitation is decreased to obtain the first yielding state. The output acceleration for 0.65g PGA is shown in Figure 35. From the near fault seismic analysis, it is predicted that the ultimate behavior is achieved when the mass is increased to the 5.5 times of its initial mass at a PGA of 1.0g and the first yielding state is achieved at 0.7 PGA. The response acceleration for yielding state and ultimate state is compared in Figure 36. The factor of safety can be calculated as the ratio of the PGA at the ultimate state to the PGA at the first yielding state. From the far field seismic analysis of nuclear containment specimen, the seismic margin is calculated as 1.43.
Conclusions
The SCS-3D program developed at the University of Houston could be used to create analytical models that accurately predict the inelastic behavior of RC shell structures. Several types of RC structures were selected to validate the analytical models including nuclear containment vessels under reversed cyclic loading. Agreements were obtained when comparing analytical results with experimental data. Overall, the primary backbone curves, response history, the initial stiffness, the peak strength, the descending branch, and the failure characteristics were accurately predicted. Hence, the FEA program (SCS) with the newly developed CSMM-based shell element is a very powerful tool to investigate the seismic behavior of RC containment structures.
In this study, the SCS-3D program was used to perform nonlinear dynamic response analyses of the 1/13th scale nuclear containment vessels subjected to far-field and near-field input accelerations. From the critical analysis of the analytical data, the safety factor for far-field and near-field input accelerations was found to be 1.54 and 1.43, respectively. The far-field response acceleration was found to be higher than the response acceleration of near-field, which was attributed to near-field input accelerations having restricted frequency content in lower frequencies as compared to far-field input accelerations.
To further validate the SCS-3D program for dynamic response prediction, a large-scale specimen will be designed based on the analyses reported in this paper. The specimen will be subjected to earthquake loading using a shake-table, and the analyses results will be compared with the experimental results.
Acknowledgement
The research described in this paper is financially supported by U.S. Department of Energy NEUP program (Project No. CFP- 13-5282). The opinions expressed in this study are those of the authors and do not necessarily reflect the views of the sponsor
References
- Banerjee AK, Holley MJ (1978) Research Requirements for Improved Design of Reinforced Concrete Containment Structures. Nuclear Engineering and Design 50(1): 33-39.
- Cook RD (2002) Concepts and Applications of Finite Element Analysis. (4thedn), Wiley, India.
- Vecchio FJ, Collins MP (1981) Stress-strain Characteristics of Reinforced Concrete in Pure Shear. IABSE Colloquium, Advanced Mechanics of Reinforced Concrete, International Association of Bridge and Structural Engin, Delft 211-225.
- Belarbi A, Hsu TTC (1995) Constitutive Laws of Softened Concrete in Biaxial Tension Compression. ACI Structural Journal 92(5): 562-573.
- Vecchio F, Collins MP (1981) Stress-Strain Characteristics of Reinforced Concrete in Pure Shear. Paper presented at the Reports of the Working Commissions (International Association for Bridge and Structural Engineering).
- Vecchio FJ, Collins MP (1982) Response of Reinforced Concrete to In Plane Shear and Normal Stresses. University of Toronto, Canada. pp. 211-225.
- Vecchio FJ (2000) Disturbed Stress Field Model for Reinforced Concrete: Formulation. Journal of Structural Engineering 126(9): 1070-1077.
- Pang XB, Hsu TTC (1995) Behavior of Reinforced Concrete Membrane Elements in Shear. ACI Structural Journal 92(6): 665-679.
- Pang XB, Hsu TTC (1996) Fixed-Angle Softened-Truss Model for Reinforced Concrete. ACI Structural Journal 93(2): 197-207.
- Hsu TTC, Zhu RRH (2002) Softened Membrane Model for Reinforced Concrete Elements in Shear. ACI Structural Journal 99(4): 460-469.
- Mansour M, Hsu TTC (2005) Behavior of Reinforced Concrete Elements under Cyclic Shear: Part 1-Experiments. Journal of Structural Engineering, ASCE 131(1): 44-53.
- Luu CH, Mo YL, Hsu TTC (2017) Development of CSMM-based Shell Element for Reinforced Concrete Structures. Engineering Structures 132: 778-790.
- Hsu TTC, Belarbi A, Xiaobo P (1995) A Universal Panel Tester. Journal of testing and evaluation 23(1): 41-49.
- Mansour M, Hsu TTC (2005a) Behavior of Reinforced Concrete Elements under Cyclic Shear. I: Experiments. Journal of Structural Engineering 131(1): 44-53.
- Pang XB, Hsu TTC (1996a) Fixed-Angle Softened-Truss Model for Reinforced Concrete. ACI Structural Journal 93(2): 197-207.
- Polak MA, Vecchio FJ (1994) Reinforced Concrete Shell Elements Subjected to Bending and Membrane Loads. ACI Structural Journal- American Concrete Institute 91(3): 261-268.
- Maekawa K, Okamura H, Pimanmas A (2003) Non-linear Mechanics of Reinforced Concrete: CRC Press p. 768.
- Yeh YK, Mo YL (1999) Full Scale Tests on Ductility, Shear Strength and Retrofit of Reinforced Concrete Hollow Columns (I).
- Yeh YK, Mo YL, Yang CY (2001) Seismic Performance of Hollow Circular Bridge Piers. ACI Structural Journal 98(6): 862-871.
- Leombruni P, Buyukozturk O, Connor JJ (1979) Analysis of Shear Transfer in Reinforced Concrete with Application to Containment Wall Specimens. Massachusetts Inst of Tech, Cambridge, USA.
- Mansour M, Hsu TTC (2005b) Behavior of Reinforced Concrete Elements under Cyclic Shear. II: Theoretical Model. Journal of Structural Engineering ASCE 131(1): 54-65.
- Zhong J (2005) Model-Based Simulation of Reinforced Concrete Plane Stress Structures. University of Houston, USA.
- Pang XB, Hsu TTC (1996b) Fixed Angle Softened Truss Model for Reinforced Concrete. ACI Structural Journal 93(2): 197-207.
- Ahmad S, Irons BM, Zienkiewicz OC (1970) Analysis of Thick and Thin Shell Structures by Curved Finite Elements. International Journal for Numerical Methods in Engineering 2(3): 419-451.
- Scordelis AC, Chan EC (1987) Nonlinear Analysis of Reinforced Concrete Shells. ACI Special Publication 98: 25-58.
- OpenSees (2013) Annual Workshop on Open System for Earthquake Engineering Simulation. Paper presented at the Pacific Earthquake Engineering Research Center, UC Berkeley, USA.
- Gao XD (1999) Framed Shear Walls under Cyclic Loading. University of Houston, USA.
- MA YL, Zhong J, Hsu TTC (2008) Seismic Simulation of RC Wall-type Structures. Engineering Structures 30(11): 3167-3175.
- C. H. Luu (2016) Development of CSMM-Based shell element for reinforced concrete structures. Department of Civil and Environmental Engineering, University of Houston.






























