Fire Induced Airflow Study: Neutral Plane Height Estimation as a Function of the Heat Source Position
Ons Tlili1*, Hatem Mhiri1 and Philippe Bournot2
1UTTPI, Ecole Nationale d'ingénieurs de Monastir, Tunisia
2IUSTI, Technopôle de Château-Gombert, France
Submission: August 12, 2017; Published: September 22, 2017
*Corresponding author: Tlili Ons, National Engineering School of Monastir (ENIM). Tunisia, Tel: 0021699249024; Email: 3philippebournot@yahoo.fr
How to cite this article: Ons T, Hatem M, Philippe B.Fire Induced Airflow Study: Neutral Plane Height Estimation as a Function of the Heat Source Position. Civil Eng Res J. 2017; 2(3): 555588. DOI: 10.19080/CERJ.2017.02.555588
Abstract
Several numerical simulations of fire induced airflow in a compartment were performed using the Fluent CFD code, in order to establish a mathematical correlation linking the neutral plane height as a critical ventilation parameter and the three-dimensional coordinates defining the fire source location within the room. The fire is modeled by a volumetric heat source (VHS approach) and the induced transport flow phenomenon is considered as a buoyancy-induced turbulent flow. Resolution of the governing equations comprises the Reynolds averaged Navier-Stokes (RANS) equations using the k-e turbulence model combined with an enhanced wall treatment.
Keywords: CFD; Neutral plane height; Fire induced flow; Correlation; Heat source location
Introduction
Fire smoke propagation inside enclosures aroused for a long time the interest of researchers who are still trying to elucidate this complex phenomenon by various methods in order to determine the smoke spread characteristics [1-4]. Researchers also count various parametric studies aiming to determine the impact of geometric and thermal parameters acting on this flow type. Steckler et al. [5] was among the first researchers who conducted a series of full-scale experiments studying the fire induced flow evolution inside a compartment as a function of several parameters like the fire strength and location and the shape and size of the openings.
Results provided by Steckler et al. [5] are regarded as the most comprehensive full-scale experimental data and are also essential for every validation task of a fire modeling codes. These experimental results were subsequently used as a database for further numerical studies as those conducted by G.M. Stavrakakis et al. [6], who based on the Steckler et al. [5] results, have developed a CFD numerical model able to properly reproduce the experimental results and to correctly predict the thermal and dynamic flow field pattern and to extend the induced fire flow study to a more complex configuration (two- room enclosure).
As fire induced flows in compartments are essentially qualified as buoyancy driven flows, these types of flows are strongly affected by the location of the heat source inside the compartment considered. Thus, investigating the fire location impact for different fire scenarios was the principle object of a large number of recent researches [7-12]. In spite of this significant number of research works on the heat source location effect, there is no direct calculating method which provides the ventilation parameters ; the flow rate at the opening and the neutral plane height as a function of the heat source position inside the enclosure.
Further to this finding and in order to complete our previous study about numerical simulation of a fire induced airflow in a compartment [13], which has only treated the mass flow rate at the opening as a crucial ventilation parameter, we propose in the present work a second general mathematical correlation between the position of the fire source inside the fire room, and the neutral plane height at the doorway exit as the second crucial ventilation parameter in a fire induced flow study.
Numerical Modeling
Physical problem
In the present study, we focus on the problem of fire induced airflow in a compartment naturally ventilated via an opening door. The expected steady flow field for the case with a central fire source is illustrated in Figure 1a. The smoke distribution is represented by the red color while the external fresh air is colored by the white one. Due to buoyancy force generated around the heat source, the fresh air enters into the room by the low part of the doorway with a flow rate noted (ma) shears or entrains some gas from the hot upper layer at a rate of (mg). This process leads to the formation of the so- called cold lower layer and the hot upper layer. Opening mass flow rates are determined by integrating the local mass velocities ( ) over the area of the door opening (H) either above or below the zero velocity plane, the so called neutral plane height (N) characterizing the height of the boundary between hot and cold layers.

Geometry and mesh
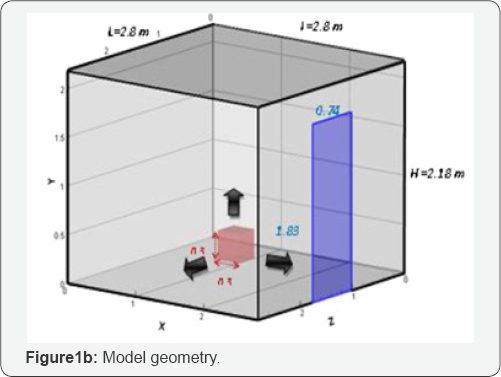
Basing on the fire room configuration adopted by Steckler et al. [5], the geometry developed in this work consists of a room (2.8 x 2.8x2.18 m3) with a centrally located cubic burner (0.3x0.3x0.3 m3) as it can be shown in Figure 1b. The burner is modeled by a volumetric heat source (VHS approach) emitting a total heat releasing rate of 62.9kW. The fire room is naturally ventilated via an opening door of dimensions (1.83x0.74 m2) as it can be shown in Figure 1b. During the simulations several positions of this burner inside the compartment were investigated corresponding in each case to the variation of the height position (y -axis variation), the transverse position (z axis variation), and the longitudinal position (x- axis variation) presenting various locations where the fire may be triggered. The three dimensional coordinates of each source position tested during the simulations are given in Table 1. The mesh grid generated for this geometric configuration is formed by 658,000 cells strongly tight in the tiles, close to the heat source, at the doorway and in the vicinity of the walls (Δ Χ= ΔΥ=10-3)

Further, the mesh grid is a little l (Δ Χ= ΔΥ=10-2)
Governing equations
Numerical simulation of the problem considered requires the resolution of the general conservation laws of mass momentum and energy namely the Navier-Stockes equations, performed taking into account the following assumptions:
a) Steady State
b) Turbulent regime
c) Incompressible fluid (air)
d) Boussinesq approximations
Given the Reynolds decomposition, the conservation equations are written as follows:
I. Mass conservation:
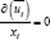
II. Momentum conservation:

Boundary conditions
Referring to the experimental data of Steckler et al. [5], the appropriate boundary conditions fixed at the domain limits are as follows:
a. The walls of the compartment are considered adiabatic
b. The burner is modeled as a volumetric heat source emitting a total power releasing of 62.9kW
c. The velocity, the temperature and the pressure outside the computational domain are taken as equal to the ambient conditions (T=300 K, P=1.01325*1005 Pa).
Computational details
The numerical resolution of the problem is performed based on a finite volume method with the segregated solver to solve the time averaged Navier Stokes equations. The standard k-£ turbulence model coupled with the Enhanced Wall Treatment approach is used to treat turbulence effects, which validity and reliability in simulating fire induced airflows in compartments were proven satisfactory in our earlier work [14] since the discrepancy noted in the flow characteristics predictions does not exceed 3%, as compared the experimental results of Steckler et al. [5]. This modification (Enhanced Wall Treatment) enables to eliminate problems occurring at the walls vicinity and ensures better accuracy of the numerical results.
To ensure accuracy of the results, the convergence criteria for the continuity, velocity and turbulence terms has been fixed in residual values to be less than 1e-04 while a value of 1e-06 is imposed for the energy.
Neutral Plane Calculation
In a case of fire, the ventilation parameters; the mass flow rate at the opening and the neutral plane height are crucial to find out. Knowing that these parameters mainly depend on the heat release rate emitted by the fire source and its location within the configuration considered as mentioned in several research works [5,8-11,15], it would be interesting to look for a mathematical correlation linking these two parameters to both of these variables. Given that in our earlier work [13], we established a first mathematical correlation allowing to calculate the mass flow rate at the doorway according to the three-dimensional coordinates of the heat source within the fire room, we propose in this present work a second mathematical correlation enabling to calculate the neutral plane height according to the heat source location within the compartment fire studied as an important parameter in a fire induced flow study, since it since characterizes the height of the boundary separating the fresh air entrance and the toxic fumes exhausting through the door. An elevated height of the neutral plane ensures a greater extent for the fresh air entrance into the compartment
In order to establish a general mathematical correlation between the neutral plane height and the heat source position within the fire room, a dimensionless analysis must drawn up: The height of the fire room, H, is taken as the characteristic length, so the dimensionless coordinates variables defining the heat source position are set as:
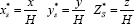
The dimensionless neutral plane height consequently becomes:
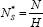
Results deduced from the various numerical simulations corresponding to the different heat source positions tested (Table 1) have provided a wide range of the neutral plane height. The different values of the neutral plane obtained, are varying according to the three-dimensional coordinates defining the heat source position within the fire room.
N*s = B x( xs* )a x(y*s )b x(Z*S )c
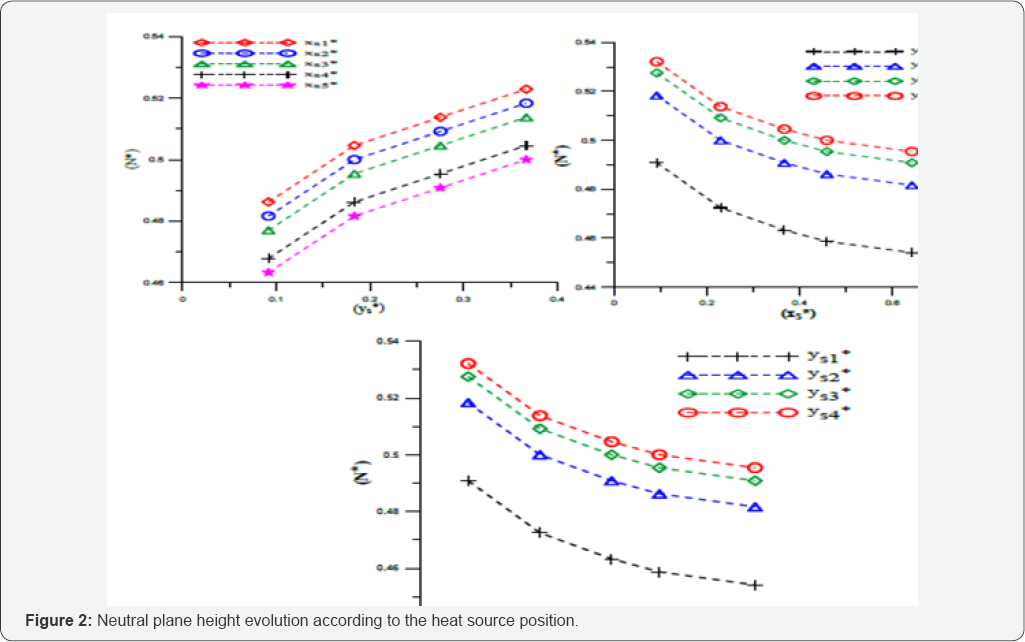
We represent in Figure 2, the evolution of the dimensionless neutral plane obtained according to the different positions of the heat source tested.
It can be clearly seen from Figure 2 that the neutral plane height decreases when the heat source is positioned at a higher transversal ( X*s) or longitudinal position ( Z*s), however it increases with the increasing of the height position of the heat * source (y*s ). But in all cases, the dimensionless variable follows a power law as a function of three dimensionless variables. This evolution has prompted us to use a logarithmic scale enabling to better follow the dimensionless neutral plane height progress (N* * ) according to different dimensionless variables defining the heat source position inside the room. This logarithmic evolution is given in Figure 3.

Profiles shown inFigure 3 , show that the dimensionless neutral plane height evolution is following a linear profile according to the three-dimensional coordinates defining the dimensionless heat source position, giving rise in each case to parallel lines having a same slope of -0.03 for the longitudinal and transversal coordinates ( X*s ) and ( Z*s ) and 0.05 for the height * position ( y*s ). Such linear logarithmic scale developments led us to seek a mathematical correlation between the neutral plane height and the dimensionless position of the heat source as follows:
The coefficients a, b and c are deducted from the slopes of the different parallel lines obtained in Figure 3, and are respectively -0.03, 0.05 and -0.03.
We can finally represent the different neutral plane height obtained from the totality of the heat source positions tested (Table 1). This final evolution is given on Figure 4.

As it can be seen from Figure 4, the dimensionless neutral plane height corresponding to the heat source positions tested during simulations can be combined into a single linear line with a slope equal to 0.525.
This linear line represents correctly and well the evolution of the dimensionless neutral plane height (N*) as a function of the heat source location since the coefficient of determination R2 is equal to 0.99. Finally, the neutral plane height can be expressed as a function of dimensionless heat source position by the following mathematical relationship:
N*s = 0.525 x( x*s )-0.03 x( y*s )x( Zs )-0.03
The established mathematical correlation can perfectly provide the value the neutral plane height in case of fire, regardless of the position of the heat source inside the compartment, which represents a very useful outcome especially for compartment fire scenarios when the heat source triggering the fire is located at a distance from the floor such as the case of a lamp, a computer or a heater rarely placed at the floor level, but usually on a table or at some height in the room. This finding would avoid engineers to optimize and to enhance fire safety measures in case of fire by determining with a simple and direct way the optimal location of smoke detectors or exhaust vents inside buildings by directly calculating the ventilation characteristics and the vents position for smoke extraction for each specific study especially without having to carry out any experimental measurements nor numerical simulations.
Conclusion
Based on the fact that the fire induced airflow in compartments mainly depends on the heat source position inside the considered configuration, and as a continuation of our earlier work [13], several CFD simulations were performed in order to find out a mathematical correlation that links the ventilation characteristics, primarily the neutral plane height at the doorway, to the heat source location within the compartment. Thus, The establishment ofthe mathematical correlation allowing to calculate the mass flow rate at the doorway according to the three-dimensional coordinates of the heat source within the fire room constitues the main finding of this research work. A CFD result obtained in this study has allowed establishing a general correlation able to calculate the neutral plane height through the doorway regardless the fire position within the fire room. Consequently, this result avoids future researches to conduct experiences or numerical simulations aiming to calculate this ventilation parameter especially when the heat source is placed at several locations in the fire room, which could be really useful to enhance fire safety measures and to provide the best location of smoke detectors or exhaust vents inside buildings by predict their optimal location for each specific case study especially when the trigger source is located at a height from the ground (lamp, computer, curtain...).
References
- Markatos NC, Cox Hydrodynamics G (1984) Heat transfer in enclosures containing a fire source. Physico Chemical Hydrodynamics 5(1): 53-66.
- McGrattan KB, Rehm RG, Baum HM (1994) Fire-driven flows in enclosures. Journal of Computational Physics 110(2): 285-291.
- Novozhilov V (2001) Computational fluid dynamics modeling of compartments fire. Progress in Energy and Combustion science 27(6): 611-666.
- Harish R, Venkatasubbaiah K (2013) Mathematical modeling and computation of fire induced turbulent flow in partial enclosures. Applied Mathematical Modelling 37: 9732-9746.
- Steckler KD, Quintiere JG, Rinkinen WJ (1982) Flow induced by fire in a compartment. National Bureau of Standards Center of fire Research NBSIR 82: 82-2520.
- Stavrakakis GM, Markatos NC (2009) Simulation in one- and two-room enclosures containing a fire source. International Journal of Heat and Mass Transfer 52: 2690-2703.
- Wang J, Hu J, Kumar K, Kumar S (2006) Evaluation of CFD Modeling Methods for Fire-induced Airflow in a Room. Journal of fire Sciences 24(5): 393-411.
- Tavelli S, Rota R, Derudi M (2014) A Critical Comparison Between CFD and Zone Models for the Consequence Analysis of Fires in Congested Environments. Chemical Engineering Transactions 36: 247-252.
- Hee-Jin Park, Holland D (2001) The effect of location of a convective heat source on displacement ventilation: CFD study. Building and Environment 36: 883-889.
- Lin YJP, Xu ZY (2013) Buoyancy-driven flows by a heat source at different levels. International Journal of Heat and Mass Transfer 58: 312-321.
- Livermore SR, Woods AW (2007) Natural ventilation of a building with heating at multiple levels. Building and Environment 42(3): 14171430.
- Jie Ji, Yanyun Fu, Kaiyuan Li, Jinhua Sun, Chuangang Fan, et al. (2015) Experimental study on behavior of sidewall fires at varying height in a corridor-like structure. Proceedings of the Combustion Institute 35: 2639-2646.
- Tlili O, Mhiri H, Bournot P (2016) Empirical correlation derived by CFD simulation on heat source location and ventilation flow rate in a fire room. Energy and Buildings 122: 80-88.
- Tlili O, Mhiri H, Bournot P (2015) Airflow induced by a room fire: Effect of roof shape and source location. International Journal of Thermal Sciences 90: 135-149.






























