Open AccessJournals | List of Open Access Journals

Research Article

Comparison between Three Soft Computing Methods in Estimating Shear Force Carried by Walls in Rough Rectangular Channels

Hossein Bonakdari*

Department of Civil Engineering, Razi University, Iran

Submission: May 26, 2017; Published: July 07, 2017

*Corresponding author: Hossein Bonakdari, Department of Civil Engineering, Razi University, Kermanshah, Iran, Tel: 988334274535; Email: bonakdari@yahoo.com

How to cite this article: Hossein B. Comparison between Three Soft Computing Methods in Estimating Shear Force Carried by Walls in Rough Rectangular Channels. Civil Eng Res J. 2017; 1(1): 555554. DOI: 10.19080/CERJ.2017.01.555554

Abstract

Estimation of shear stress is an important subject in hydraulic engineering, since it affects the flow structure directly. In this study, Support Vector Machine (SVM), Genetic Algorithm Artificial neural network (GAA) as a hybrid method of Artificial Neural Network (ANN)-modified Ge–netic Algorithm (GA) and Genetic Programming (GP) models was used and compared for predicting the percentage of shear force carried by walls (%SF_w) in a rectangular channel with rough boundaries.

Introduction

Sediment load using Shear stress comprises basic information for predicting average depth velocity and discharge in channels. With knowledge of the percentage of shear force carried by walls (%SF_w) it is possible to more accurately estimate shear stress values. Many direct and indirect methods have been used to calculate the shear stress along a wetted perimeter in different channel cross sections Knight [1]. Since the experimental estimation of boundary shear stress is a difficult and time consuming procedure, other researchers have attempted to calculate boundary shear stress by analytical and numerical methods (e.g. Berlamont et al. [2], Sheikh & Bonakdari [3] and Bonakdar et al. [4,5]). The use of soft computing technique in modeling complicated problems is recently expanding.

Kisi et al. [6] estimated daily suspended a GP model. They also compared this method with several soft computing techniques and deducted that the GP model operates better than the others. Huai et al. [7] used the ANN model to estimate the apparent shear stress acting at the vertical line between subareas of a compound channel’s cross section. The shear stress is a very important parameter in channel problems but only few studies have dealt with estimating the percentage of shear force in channels. Cobaner et al. [8] utilized an ANN model in order to estimate the sheer force carried by walls in rectangular channels and ducts. The SVM is a new approach and branch of soft computing used for modeling different hydraulic and hydrology phenomena Kisi & Cimen [9].

The objective of this study is to investigate the ability and accuracy of Support Vector Machine (SVM), Genetic Algorithm Artificial neural network (GAA) as a hybrid method of Artificial Neural Network (ANN)-modified Genetic Algorithm (GA) and Genetic Programming (GP) models to predict the percentage of shear force carried by walls (%SF_w) in a rectangular channel with rough boundaries. Also the comparison between the best of each method was done to select the most appropriate method in predicting %SFw.

Methodology

GP model

The Genetic Programming (GP) is one of the practical applications of the genetic algorithm, introduced by Koza [10]. The GP method is very similar to the GA algorithm, except that the chromosomes are actually computer programs. GP starts out with a random initial population consisting of some computer programs. Then, by running each computer program, the cost of each one of the chromosomes is evaluated. Calculating the cost function is done by using the fitness functions. So, by sorting out the initial population costs and perform the crossover, the mutation and elite processes of GA, the new population is achieved. The main objective of the GP is to find a computer program that could predict accurately the shear force by using the input variables.

GAA model

Artificial Neural Network (ANN) as a well-known soft computing method was used in different fields of the engineering problems. A typical ANN formed of three or four layers, one input layer, one or two hidden layers and one output layer. Each layer consists of some neurons, each neuron counting the weighted summation of the neurons in the previous layer and, after putting this summation into the transfer function, giving the results to the neurons of the next layer. The weight of each neuron is determined in the training process. In this study, the Levenberg–Marquardt Algorithm Levenberg [11] was used for training the ANN models. In addition to the advantages of the ANN method in modeling the complex problems, the absence of a specific rule in choosing the number of hidden layer nodes makes the modeling process more puzzling. In this study, a modified GA was used to optimize the structure of the ANN method. The GA investigates the different ANN models with a various number of neurons in hidden layers and automatically chooses the most appropriate one.

SVM model

The simulation branch of SVM that is applied to regression problems is called Support Vector Regression (SVR). SVR is used to find a relation between the input variables of and the observed variables of T = {t₁, t₁,....t_n } . Therefore, SVR can predict the output vector of O = {o_1,o_{2 ,}....o_n } by using the input variables. When O is closer to T, the SVR model has higher performance. The inputs of this study are and the output is the percentage of shear force carried by walls (%SF_w).

Data used

The data measured by Knight (1981) in rough rectangular channels were used in order to predict %SFw with the SVM model. Knight (1981) conducted the experiments in a flume with 15m long, 460mm wide, on a constant bed slope of 9.58x10-4. The wall and bed shear force was measured by Preston tube technique and the percentage of shear force carried by walls for different flow depths was also measured.

Results

In order to predict percentage of shear force (%SF_w) by models, four important variables in shear stress in channels were used. These dimensionless variables are aspect ratio (b/h), Froude Number (Fr), Reynolds Number (Re) and relative roughness (ksb/ksw) also eight input combinations of these variables in modeling procedure with each model were examined. In modeling with GP and GAA two fitness functions as Mean Squared Error (MSE) and Mean Absolute Error (MAE) were studied. Also in modeling with SVM eight different kernel functions for selecting the best of them were investigated. Finally the GP model with selection of b/h, Fr and Re as input combination, MAE as fitness function and mathematical function showed the best results between other GP models.

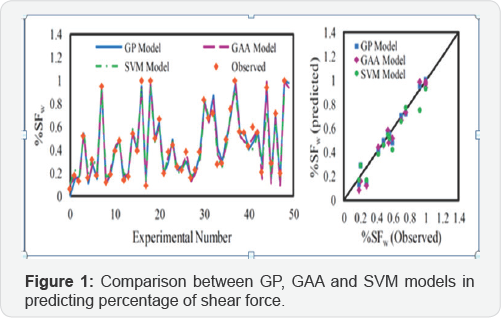
In modeling with GAA, the model with ksb/ksw, Fr and Re as input combination, MSE as fitness function and logarithmic transfer function in both hidden layer and output layer performed better than other GAA models. In modeling with SVM the model with exponential kernel function and b/h, Fr and Re as input combination showed the most accurate results than other models of SVM. Figure 1 shows the comparison between the most appropriate of three mentioned models as hydrograph for all data sets and scatter plot for test data set. As seen in Figure 1 all models showed the high performance in predicting percentage of shear force and in scatter plot the results of models is very close to fitted line but the GP model with RMSE of 0.0515 performed better than GAA and SVM models with RMSE of 0.0672 and 0.0870 respectively.